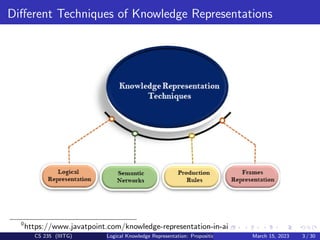
This document provides an overview of propositional logic as a technique for logical knowledge representation. It defines key concepts like propositions, logical connectives, and properties of propositional logic. Examples of deduction rules like modus ponens and modus tollens are also described. The document concludes by using propositional logic to represent the classic game "The Wumpus World", where the goal is to deduce the location of threats like a monster and pits to safely find gold.

1. Logical Knowledge Representation: Propositional Logic
Instructors: Soumi Chattopadhyay
Indian Institute of Information Technology Guwahati
March 15, 2023
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 1 / 30

2. Overview
1 Introduction
2 Logical Representation
3 Logical Representation: Advantages and Disadvantages
4 Propositional Logic
5 Properties of Propositional Logic
6 Logical Connectives
7 Properties of Logical Operators
8 Properties of Boolean Formula
9 Deduction using Propositional Logic
10 Limitation of Propositional Logic
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 2 / 30

3. Different Techniques of Knowledge Representations
0
https://www.javatpoint.com/knowledge-representation-in-ai
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 3 / 30

4. Logical Representation
Logical Knowledge representation
Consists of precisely defined syntax and semantics supporting the
sound inference
Some concrete rules, deal with propositions
No ambiguity in representation
Draws a conclusion based on various conditions
Syntax
The rules to construct legal sentences in the logic
Determines symbols can be used in knowledge representation
Determines how to write those symbols
Semantics
The rules to interpret the sentence in the logic
Assigns a meaning to each legal sentence
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 4 / 30

5. Logical Representation: Advantages and Disadvantages
Advantages
Logical representation enables to do logical reasoning
Logical representation is the basis for the programming languages
Disadvantages
Have some restrictions and are challenging to work with
May not be very natural, and inference may not be so efficient
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 5 / 30

6. Propositional Logic
Proposition
A declarative statement which is either true or false
Propositional Logic
A technique of knowledge representation in logical and mathematical
form
The simplest form of logic
All the statements are made by propositions
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 6 / 30

7. Properties of Propositional Logic
Propositional Logic
Also called Boolean logic as it works on 0 and 1
Can be either true or false, but it cannot be both
Consists of an object, relations or function, and logical connectives
Connectives are also called logical operators
The propositions and connectives are the basic elements of the
propositional logic
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 7 / 30

8. Logical Connectives
Used to connect two simpler propositions
Let A and B are two propositions
Symbol Name Technical term Syntax
¬ NOT Negation ¬A or Ā
∨ OR Disjunction A ∨ B
∧ AND Conjunction A ∧ B
→ Implies Implication A → B
↔ If and only if Biconditional A ↔ B
Precedence of logical connectives:
1st
Precedence: Parenthesis 2nd
Precedence: Negation
3rd
Precedence: AND 4th
Precedence: OR
5th
Precedence: Implication 6th
Precedence: Biconditional
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 8 / 30

9. Logical Connectives
Let A and B are two propositions
A B Ā A ∨ B A ∧ B A → B A ↔ B
False False True False False True True
False True True True False True False
True False False True False Flase False
True True False True True True True
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 9 / 30

10. Topics of Propositions
Two Types of Propositions
Atomic propositions: Consists of a single proposition symbol
Compound propositions: Constructed by combining atomic
propositions, using parenthesis and logical connectives
Logical Equivalence
A → B is logically equivalent to Ā ∨ B (Try to check using truth
table!)
A ↔ B is logically equivalent to (A → B) ∧ (B → A) (Try to check
using truth table!)
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 10 / 30

11. Properties of Logical Operators
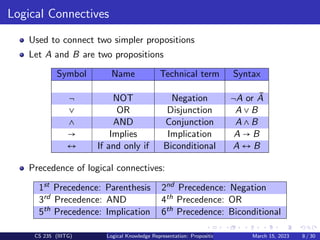
Commutativity:
A ∨ B ≡ B ∨ A [≡ stand for equivalent]
A ∧ B ≡ B ∧ A
Associativity:
(A ∨ B) ∨ C ≡ A ∨ (B ∨ C)
(A ∧ B) ∧ C ≡ A ∧ (B ∧ C)
Identity element:
(A ∨ True) = True
(A ∧ True) = A
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 11 / 30

12. Properties of Logical Operators
Distributive:
A ∧ (B ∨ C) ≡ (A ∧ B) ∨ (A ∧ C)
A ∨ (B ∧ C) ≡ (A ∨ B) ∧ (A ∨ C)
DE Morgan’s Law:
¬(A ∨ B) ≡ (¬A) ∧ (¬B) [≡ stand for equivalent]
¬(A ∧ B) ≡ (¬A) ∨ (¬B)
Double-Negation:
¬(¬A) ≡ A
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 12 / 30

13. Properties of Boolean Formula
Valid / Tautology
A proposition formula which is always true (for all assignments of all
Boolean variables)
Example: ((A → B) ∧ A) → B (Try to check yourself!)
Contradiction / Unsatisfiable
A proposition formula which is always false (for all assignments of all
Boolean variables)
Example: A ∧ ¬A (Try to check yourself!)
Satisfiable
A proposition formula which is true for at-least one assignment of its
variables
Example: ((A → B) ∧ ¬A) → ¬B (Try to check yourself!)
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 13 / 30

14. Deduction using Propositional Logic
Inference
Generating the conclusions from evidence and facts
Inference rules
The templates for generating valid arguments
Applied to derive proofs in AI
The proof is a sequence of the conclusion that leads to the desired goal
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 14 / 30

15. Deduction using Propositional Logic
Some terminologies related to inference rules:
Implication: A logical connectives, represented as A → B, a Boolean
expression
Converse: The converse of implication can be written as B → A
Inverse: The negation of implication is called inverse, represented as
¬A → ¬B
Contrapositive: The negation of converse is termed as
contrapositive, represented as ¬B → ¬A
Note: Implication and its contrapositive are equivalent
You can show this by proving
Implication and its contrapositive are equivalent
(A → B) ↔ (¬B → ¬A) is valid / tautology
(Try to check yourself using truth table!)
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 15 / 30

16. Rule of Deduction using Propositional Logic
Modus Ponens: If A and A → B are true, we can infer B to be true.
It can be represented as:
(A → B),A
˙
. . B
Justification:
A B A → B (A → B) ∧ A
False False True False
False True True False
True False False False
True True True True
In modus ponens, we assume as premises that A → B is true and A is true.
Only one line of the truth table (the last row) satisfies these two
conditions. On this line, B is also true. Therefore, whenever A → B and A
are true, B has to be true.
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 16 / 30

17. Rule of Deduction using Propositional Logic
Modus Tollens:
(A → B),¬B
˙
. . ¬A
Hypothetical Syllogism:
(A → B),(B → C)
˙
. . (A → C)
Disjunctive Syllogism:
(A ∨ B),¬A
˙
. . B
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 17 / 30

18. Rule of Deduction using Propositional Logic
Constructive Dilemma:
(A → B) ∧ (C → D),(A ∨ C)
˙
. . (B ∨ D)
Destructive Dilemma:
(A → B) ∧ (C → D),(¬B ∨ ¬D)
˙
. . (¬A ∨ ¬C)
Simplification:
A ∧ B
˙
. . A
or
A ∧ B
˙
. . B
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 18 / 30

19. Rule of Deduction using Propositional Logic
Conjunction:
A,B
˙
. . (A ∧ B)
Addition:
A
˙
. . (A ∨ B)
Resolution:
(A ∨ B),(¬A ∧ C)
˙
. . (B ∨ C)
Natural Deduction is Sound and Complete
(Try to justify yourself using truth table!)
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 19 / 30

20. An example: The Wumpus World
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 20 / 30

21. The Wumpus World: Description of the Game
The Wumpus world
A cave with 4 × 4 rooms connected with passageways
16 rooms in total connected with each other
The cave has a room with a beast Wumpus
Can eat anyone who enters the room
Can be shot by the agent
The agent has a single arrow
In the Wumpus world, there are some Pits
Rooms which are bottomless
If agent falls in Pits, he will be stuck there forever
In one room there is a possibility of finding a heap of gold
The goal of the agent is
To find the gold and climb out the cave without fallen into Pits or
eaten by Wumpus
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 21 / 30

22. The Wumpus World: Description of the Game
The rooms adjacent to the Wumpus room are smelly, so that it would
have some stench
The room adjacent to PITs has a breeze, so if the agent reaches near
to PIT, then he will perceive the breeze
There will be glitter in the room if and only if the room has gold
The Wumpus can be killed by the agent if the agent is facing to it,
and Wumpus will emit a horrible scream which can be heard
anywhere in the cave
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 22 / 30

23. The Wumpus World: Game Environment
Game Environment
A 4 × 4 grid of rooms
The agent initially in room square [1,1], facing toward the right
Location of Wumpus and gold are [3,1] and [3,2] respectively
Agent has following actions
Left turn
Right turn
Move forward
Grab
Release
Shoot
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 23 / 30

24. The Wumpus World: Game Environment
Agent has following sensors
Perceive the stench if he is in the room adjacent to the Wumpus
Perceive breeze if he is in the room directly adjacent to the Pit
Perceive the bump if he walks into a wall
When the Wumpus is shot, it emits a horrible scream which can be
perceived anywhere in the cave
To prove
Agent can identify that the Wumpus is in the room [3,1]
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 24 / 30

25. The Wumpus World: Some Properties
Some Properties of the game
Partially observable: The Wumpus world is partially observable
because the agent can only perceive the close environment such as an
adjacent room
Deterministic: It is deterministic, as the result and outcome of the
world are already known
Sequential: The order is important, so it is sequential
Static: It is static as Wumpus and Pits are not moving
Discrete: The environment is discrete
One agent: The environment is a single agent as we have one agent
only and Wumpus is not considered as an agent
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 25 / 30

26. The Wumpus World: Model the problem
Atomic proposition variable for Wumpus world
Pij ∶ be true if there is a Pit in the room [i,j]
Bij ∶ be true if breeze can be perceived in [i,j]
Wij ∶ be true if there is wumpus in [i,j]
Sij ∶ be true if stench can be perceived in [i,j]
Vij ∶ be true if [i,j] is visited by the agent
Gij ∶ be true if there is gold in [i,j]
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 26 / 30

27. The Wumpus World: Model the problem
Some propositional Rules for the wumpus world:
No breeze in [i,j], implies there is no Pit in the neighbour
¬Bij → ¬Pi+1,j ∧ ¬Pi−1,j ∧ ¬Pi,j+1 ∧ ¬Pi,j−1 (1)
Breeze in [i,j], implies there is a Pit in the neighbour square
Bij → Pi+1,j ∨ Pi−1,j ∨ Pi,j+1 ∨ Pi,j−1 (2)
No stench in [i,j], implies wumpus is not in the neighbour
¬Sij → ¬Wi+1,j ∧ ¬Wi−1,j ∧ ¬Wi,j+1 ∧ ¬Wi,j−1 (3)
Stench in [i,j], implies the wumpus is in the neighbour square
Sij → Wi+1,j ∨ Wi−1,j ∨ Wi,j+1 ∨ Wi,j−1 (4)
The agent is in [1,1] (starting position), therefore, we have following facts
¬W11; ¬S11; ¬P11
Please be careful regarding the boundary condition!
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 27 / 30

28. The Wumpus World: Deduction
¬S11 → ¬W12 ∧ ¬W21 ¬S11
¬W12 ∧ ¬W21
¬W12 ¬W21 ¬S12 → ¬W11 ∧ ¬W22 ∧ ¬W13
¬B11 → ¬P12 ∧ ¬P21
¬W11 ¬P11
¬P12 ∧ ¬P21
¬P12 ¬P21
¬W11 ∧ ¬W22 ∧ ¬W13
¬W12 ¬W21 ¬W22 ¬W13 ¬P12 ¬P21
S21 → W11 ∨ W22 ∨ W31
¬W12 ¬W21 ¬W22 ¬W13 ¬P12 ¬P21
W11 ∨ W22 ∨ W31
¬W11
W31
: Facts
: Knowledge base
: Inference
(Using Modus Ponens)
(Using Simplification)
(Using Modus Ponens)
(Using Simplification)
(Using Modus Ponens)
(Using Disjunctive Syllogism)
** There are other inferences as well
However, for this proof whatever is required
we consider that only
(Using Modus Ponens)
(Using Simplification)
¬S12
No Pit, No Wumpus
Agent can move to [1, 2]
No Pit, No Wumpus
Agent can move to [2, 1]
S21
Wumpus is in [3, 1]
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 28 / 30

29. Limitation of Propositional Logic
Propositional logic has limited expressive power
We cannot represent relations like ALL, some, or none with
propositional logic. Example:
All students are reading the lectures
Some students are working hard
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 29 / 30

30. Thank You!
CS 235 (IIITG) Logical Knowledge Representation: Propositional Logic March 15, 2023 30 / 30