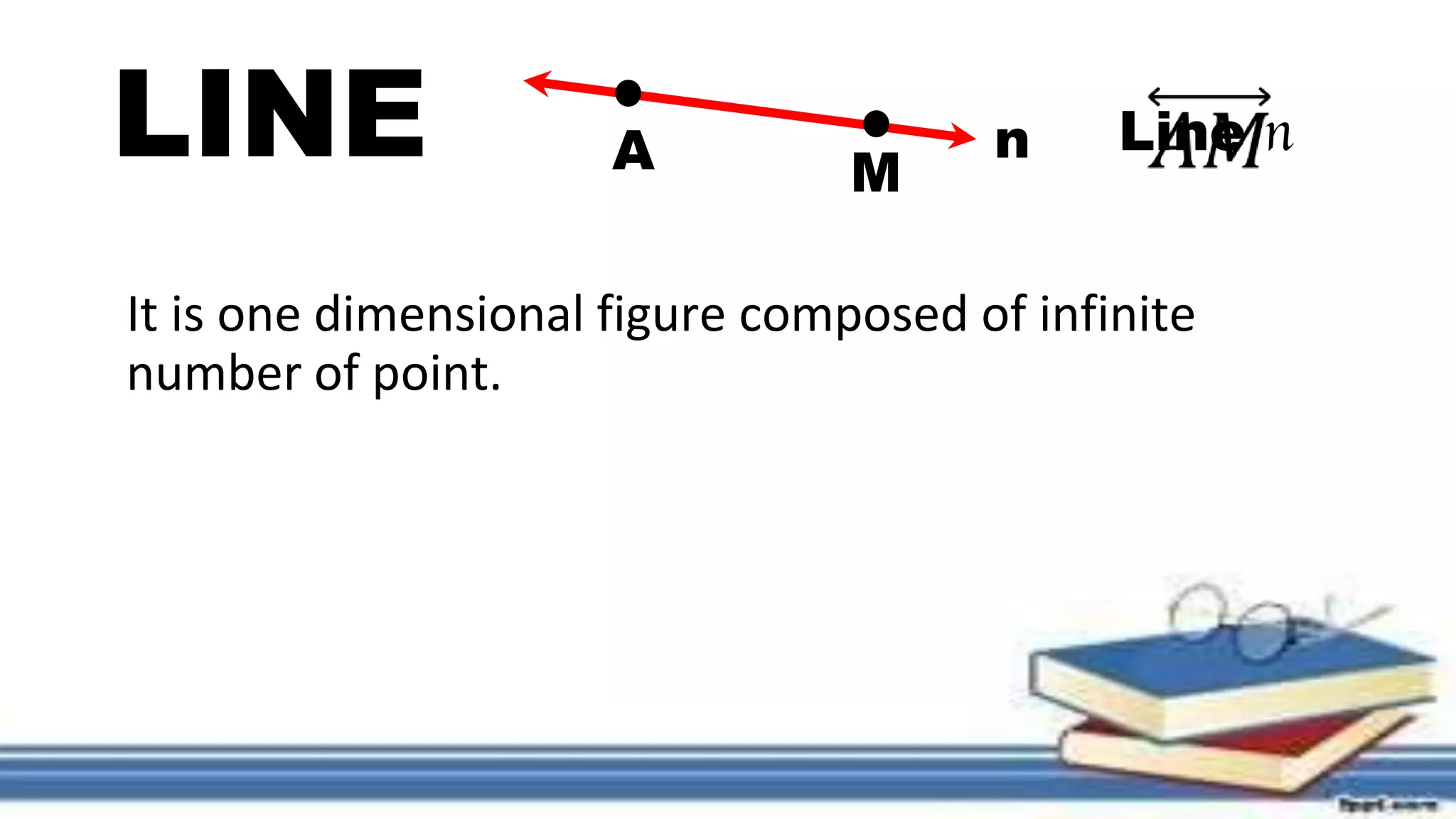
This document defines key terms in mathematical systems and axiomatic structures. It explains that a mathematical system provides order and procedures for a discipline using axioms and undefined terms. Axioms are statements accepted as true without proof that are used to derive theorems. Undefined terms include points, lines, and planes. Postulates are also accepted as true without proof, while theorems must be proven; corollaries directly follow from theorems and lemmas are used to prove other theorems.

1. SUBJECT TEACHER: MR. JERICHO B. NADANZA
GRADE 8 - MATH

2. MATHEMATICA
L SYSTEM

3. A Mathematical System is a set of
structures designed to provide order and
procedural operation in certain
discipline.

4. Axiomatic Structure or Axiomatic
System
It refers to any set of axioms from
which other axioms can be used
in conjunction with derived
theorems.

5. Axioms
Mathematical Statement that serve as
an entry statement in deriving other
logically derived statements.

6. UNDEFINED TERMS

7. POINT ●
It is something having specific position
but without deminsion, magnitude,
direction.
G Point G

8. LINE
It is one dimensional figure composed of infinite
number of point.
A M
n Line n

9. PLANE
It is usually represented by flat surface where
infinite number of lines can lie.

10. POSTULATE, THEOREM AND
COROLLARY

11. POSTULATE
A statement that accepted as true
without proof.

12. THEOREM
A statement that need or can be proven.

13. COROLLARY
It is a theorem that is direct consequence
of another theorem

14. LEMMA
It is a theorem used as a stepping stone
to prove later the others.