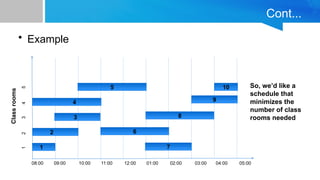
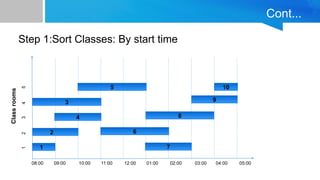
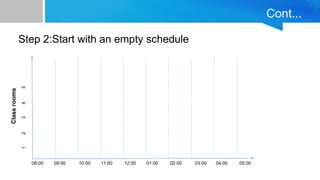
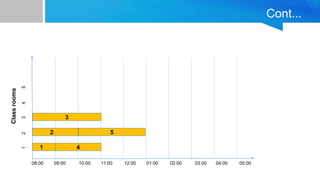
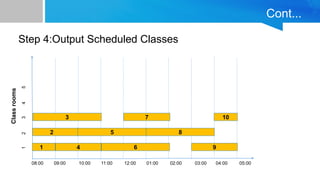
The document outlines a greedy algorithm for solving class scheduling problems, emphasizing its characteristics such as making locally optimal choices and its efficiency. It provides a structured approach for maximizing the number of non-overlapping classes while minimizing classroom usage, including steps, pseudocode, and examples. Limitations of the greedy algorithm are also discussed, highlighting its potential shortcomings in complex scenarios.

1. A greedy algorithm for class scheduling
problems

2. Outline
1. What is Greedy algorithm
2. Characteristics
3. Greedy algorithm for class scheduling problems
4. Pseudocode implementation
5. Limitations of Greedy Algorithm
6. Conclusion

3. What is greedy algorithm?
• Greedy algorithms are a class of algorithms that make
locally optimal choices at each step with the hope of
finding a global optimum solution.
• Powerful tool for solving optimization problems

4. Characteristics
• Local optimal choices
• Fast and simple to implement
• Greedy Choice Property
• Optimal Substructure
• Iterative Process
• No Backtracking

5. Greedy algorithm for class scheduling problems
• Class scheduling involves allocating resources (classrooms,
timeslots) to classes efficiently.
• Objective: Maximize the number of non-overlapping classes
scheduled
• Each class has a start and an end time.
• Classes cannot overlap
Importance
• Minimizes conflicts
• Optimizes resource usage
• Simplifies planning

6. Describe a problem
Imagine:
• There are 10 lectures, each with a fixed start and end
time.
• Each lecture needs a class rooms .
• There can only be one lecture in one class rooms at the
same time.
• We want to find the minimum number of class rooms
needed for scheduling all lectures

7. Cont...
• Example
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1 7
2
3
6
4
5
8
9
1
2
3
4
5
So, we’d like a
schedule that
minimizes the
number of class
rooms needed
10

8. Cont...
Step 1:Sort Classes: By start time
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1 7
2
4
6
3
5
8
9
1
2
3
4
5
10

9. Cont...
Step 2:Start with an empty schedule
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
2
3
4
5

10. Cont...
Step 3: Iterate Through Classes:
• For each class in the sorted list:
Check each classroom (up to 5):
If a classroom is available (i.e., its end time is less
than or equal to the start time of the class), assign the
class to that classroom and update the end time of that
classroom to the end time of the scheduled class.

11. Cont...
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
1
2
3
4
5

12. Cont...
Step 1:Sort Classes: By end time
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
2
1
2
3
4
5

13. Cont...
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
2
3
1
2
3
4
5

14. Cont...
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
2
3
1
2
3
4
5
4

15. Cont...
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
2
3
1
2
3
4
5
4
5

16. Cont...
Step 4:Output Scheduled Classes
08:00 09:00 10:00 11:00 12:00 01:00 02:00 03:00 04:00 05:00
Class
rooms
1
7
2
4 6
3
5 8
9
1
2
3
4
5
10

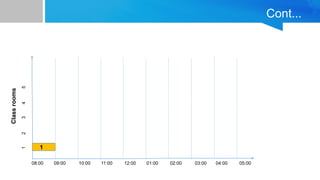
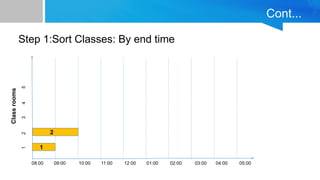
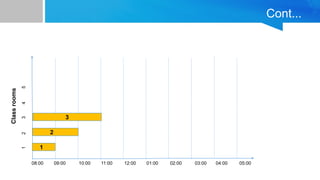
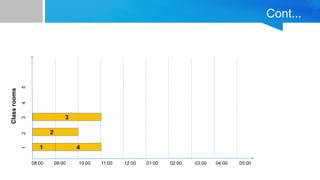
17. Pseudocode implementation of the greedy scheduling algorithm
class Class:
int startTime
int endTime
function scheduleClasses(classes, numClassrooms):
sort(classes)
classrooms = array of size numClassrooms with all elements set to 0
schedule = empty list
for each class in classes:
for i from 0 to numClassrooms - 1:
if classrooms[i] <= class.startTime: // Check if classroom is free
schedule.append((class, i))
classrooms[i] = class.endTime
break
return schedule

18. Limitations of Greedy Algorithm
• Local Optimality: Focuses on immediate benefits,
potentially missing the global optimum.
• Specificity: May not work well for complex constraints
(e.g., teacher availability, specific room requirements).
• Limited Flexibility: Needs careful selection of sorting
criteria.

19. Conclusion
• Greedy algorithms provide a simple, efficient solution for
class scheduling.Best suited for problems with
straightforward constraints.

20. Thank you