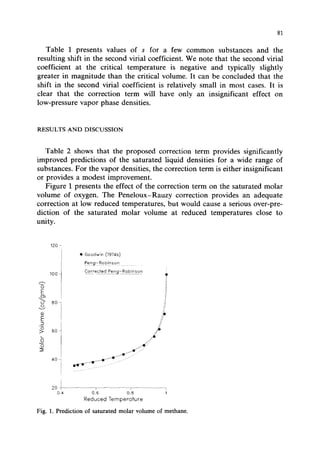
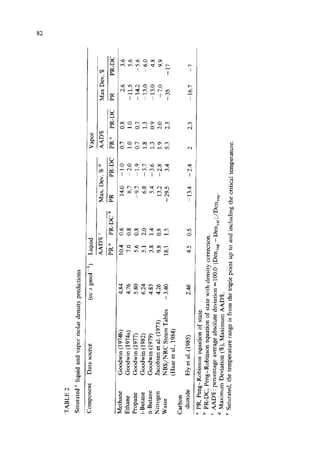
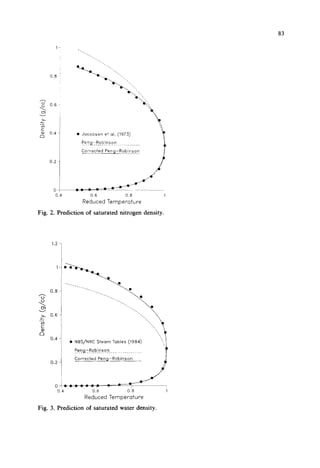
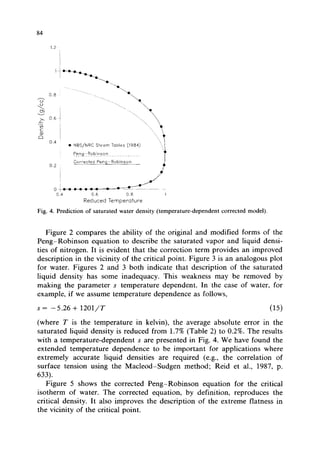
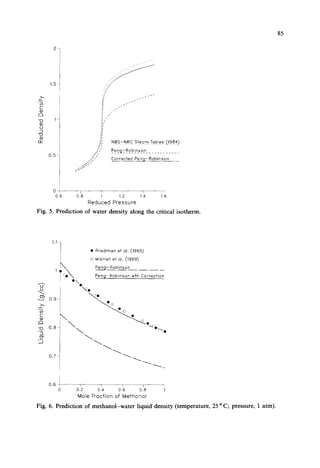
This document presents a density correction for the Peng-Robinson equation of state. The correction involves adding a simple empirical term that requires one parameter per component. It improves the prediction of liquid densities by 2-4% and vapor densities slightly. The correction retains the internal consistency between vapor and liquid properties predicted by equations of state. It provides a reliable way to enhance density predictions without significantly affecting other properties.

1. Fluid Phase Equilibria, 47 (1989) 77-87
Elsevier Science Publishers B.V., Amsterdam - Printed in The Netherlands
77
A DENSITY CORRECTION FOR THE PENG-ROBINSON EQUATION
OF STATE
PAUL M. MATHIAS, TARIK NAHEIRI and EDWIN M. OH
Air Products and Chemicals, Inc., P.O. Box 538, Allentown, PA 18105 (U.S.A.)
(Received January 12, 1988; accepted in final form November 25, 1988)
ABSTRACT
Mathias, P.M., Naheiri, T. and Oh, E.M., 1989. A density correction for the Peng-Robinson
equation of state. Fluid Phase Equilibria, 47: 77-87.
A simple empirical additive term is proposed which corrects the liquid molar volumes
predicted by the Peng-Robinson equation of state. The correction term requires only a single
parameter for each component and is applicable to mixtures containing polar as well as
non-polar substances. The corrected model predicts vapor and liquid densities to within
2%4% of experimental data. A similar correction is applicable to other equations of state.
INTRODUCTION
Equations of state like those proposed by Soave (1971) and Peng and
Robinson (1976) are in widespread use for engineering applications. These
simple models overcome their poor theoretical basis (Henderson, 1979) by
optimizing their description of pure-component vapor pressures and the
vapor-liquid equilibrium of mixtures. As a result, however, the predictions
of other properties like density are relatively poor, especially for polar
components. The Soave and Peng-Robinson models have two constants and
therefore are forced to predict a universal value of the critical compressibil-
ity factor. Investigators like Fuller (1976), Martin (1979), Schmidt and
Wenzel (1980) and Pate1 and Teja (1982) have introduced a third parameter
to produce a model capable of simultaneous prediction of all thermody-
namic properties. These researchers have managed to obtain only modest
improvements in density predictions. In particular, they have found that if
the value of the third parameter is chosen such that the true critical
compressibility factor is reproduced, the predictions of liquid density be-
come poor.
Fuller (1976), Yarborough (1979) and Morris and Turek (1986) have
suggested extended temperature dependence of the equation of state con-

2. 78
stants to obtain better description of both vapor pressure and molar volume.
But these models generally have discontinuities or at least sharp and
unphysical temperature variation around the critical region. Further, this
approach can result in physically unrealistic negative predictions for heat
capacities (Trebble and Bishnoi, 1986).
It is evident that the theoretical deficiency of these models precludes
simultaneous prediction of all thermodynamic properties. We thus propose a
correction term to improve the density predictions of existing models. The
correction is applied to the Peng-Robinson equation of state. In principle, it
is also applicable to any other equation of state.
The density correction term presented in this work is an extension of the
“volume-translation” idea proposed by Peneloux and Rauzy (1982). It is
virtually identical to the Peneloux-Rauzy correction for incompressible
liquids and is a significant improvement near the critical point where liquids
are compressible.
MOLAR VOLUME CORRECTION TERM
According to the Peng-Robinson (1976) equation of state, the pressure of
a pure fluid is given as a function of temperature and molar volume as
follows
RT
p=--
u-b u(u+b):b(u-b)
(1)
where a and b are component-dependent parameters; b is independent of
temperature and a is temperature dependent such that the vapor pressure of
the pure fluid is accurately correlated. Thus,
b = 0.07780 RTJP, (2)
a = d(T) (3)
a, = 0.45724 R2Tc2/Pc (4)
p = [l +c& - T;‘=) + c2(1 - T;12)2 + c&l - Ti’2)3]2
Equation (5), which was proposed by Mathias and Copeman (1983), is
slightly different from that originally proposed by Peng and Robinson
(1976). The original model is obtained when c2 = c3 = 0. The additional
parameters are useful to correlate the vapor pressure data of highly polar
substances like water and methanol.
Equations (l)-(5) provide a good fit of the vapor pressure for most
substances, but the prediction of molar volumes can be seriously in error. In
particular, the prediction of saturated liquid molar volumes can be in error

3. 79
by lo-40%. Comparison between experimental data and Peng-Robinson
predictions for liquid molar volumes shows that, to a reasonable approxima-
tion, the difference is constant for temperatures ranging from the triple
point to a reduced temperature of about 0.85. An effective correction term
has already been suggested by Peneloux and Rauzy (1982).
V =Orr = V + s
(6)
where s is a small molar volume correction term that is component depen-
dent; u is the molar volume predicted by eqn. (1) and vCorTrefers to the
corrected molar volume.
Examination of the value of s for several substances indicates that its
value is positive for the smaller nonpolar substances (oxygen, nitrogen and
paraffins up to n-pentane), but negative for the higher molecular weight
nonpolars and essentially for all polar substances. After the correction of
eqn. (6) has been applied, the liquid molar volume error pattern is similar
for all substances. vco”‘ rises above the experimental value at a reduced
temperature of approximately 0.85, and the difference increases to a maxi-
mum value at the critical temperature.
An additional correction term is necessary in the vicinity of the critical
point. After evaluating several alternate forms, we propose a correction as
follows
(7)
where 6 is the bulk modulus, a dimensionless quantity related to the inverse
of the isothermal compressibility.
6 is an appropriate function for use in eqn. (7) because it is always positive
for physically meaningful solutions of eqn. (1); its value is relatively high at
low reduced temperatures where eqn. (6) is an adequate correction and its
variation with reduced temperature allows an extremely simple correction
term. The constant 0.41 was determined by regressing data for many
substances, and f, was chosen such that the true critical volume is obtained.
By definition,
f,=zJ,-(Vc’R$_S) (9)
=v,-(3.946b+s) (IO)
In eqn. (10) we have used the relation between the mechanical critical
volume predicted by the Peng-Robinson equation and parameter b. Equa-
tion (7) describes the correction term we propose for pure fluids. In addition

4. 80
to the parameters required by the Peng-Robinson equation, the component
critical volume u,, and the empirical parameter s are required.
The correction term is also applicable to mixtures. The quantities u and 6
are determined by the mixing rule chosen for the Peng-Robinson model. In
addition, we propose the simplest possible mixing rules for s and u,,
s = cx,si
UC= CXPci
(11)
(12)
EFFECT ON VAPOR PHASE DENSITIES
A key advantage of equations of state is that they provide continuity
between vapor and liquid properties at the critical point. In order to retain
this continuity, eqn. (7) must also be applied to the vapor phase. It is
therefore important to analyze the effect of the correction term on vapor
phase densities.
Useful insight into the effect of eqn. (7) on vapor phase densities is
obtained by examining its low density limit
Equation (13) is derived by expanding eqn. (7) about the ideal-gas limit and
retaining only terms that are first order in pressure. The second term on the
right-hand side of eqn. (13) is the contribution due to the second virial
coefficient of the unmodified Peng-Robinson equation. Thus, the third term
shifts the second virial coefficient as follows
B =Orr= s +
0.41
-fc1.41
TABLE 1
Effect of correction term on vapor phase densities: shift in the second virial coefficient
Component s K BCO”
(cm3 mol-‘) (cm mol-‘) (cm3 mol-‘)
Methane 4.84 99.1
Ethane 4.76 147.8
Propane 5.80 200.9
i-Butane 6.24 263.0
n-Butane 4.83 255.5
Nitrogen 4.26 90.1
Water - 3.40 55.9
Carbon dioxide 1.56 94.1
1.7
-0.1
- 2.0
- 2.1
- 5.6
1.6
- 7.9
-2.5

5. 81
Table 1 presents values of s for a few common substances and the
resulting shift in the second virial coefficient. We note that the second virial
coefficient at the critical temperature is negative and typically slightly
greater in magnitude than the critical volume. It can be concluded that the
shift in the second virial coefficient is relatively small in most cases. It is
clear that the correction term will have only an insignificant effect on
low-pressure vapor phase densities.
RESULTS AND DISCUSSION
Table 2 shows that the proposed correction term provides significantly
improved predictions of the saturated liquid densities for a wide range of
substances. For the vapor densities, the correction term is either insignificant
or provides a modest improvement.
Figure 1 presents the effect of the correction term on the saturated molar
volume of oxygen. The Peneloux-Rauzy correction provides an adequate
correction at low reduced temperatures, but would cause a serious over-pre-
diction of the saturated molar volume at reduced temperatures close to
l Goodwin (1974b)
Peng-Robinson
Corrected Peng-Robinson
?
0.‘6 0.8 1
Reduced Temperature
Fig. 1. Prediction of saturated molar volume of methane.

6. 82
t"-I
<
0
u
0
7 a
0
e~
e
i I I I I I I
I I I I I I I
I I
I
I~ t"-- ~ t"- ,-.~
O 0 O O 0
0 0 0 0 o~.-~, ~ ;~
o
;, o
~. o
I.) """
o ~.~

7. 83
PengpRobinson
Corrected Peng-Robinson
0.4 0.6 0.8 1
Reduced Temperature
Fig. 2. Prediction of saturated nitrogen density.
1.2
1
0.2
0
1-
11
IL
34
. NBS/NRC Steam Tables (1984)
Peng-Robinson
Corrected Peng-Robinson
0.6 0.8 1
Reduced Temperature
Fig. 3. Prediction of saturated water density.

8. 84
1.2
Correcied Peng-Robinson
0.4 0.6 0.8 1
Reduced Temperature
Fig. 4. Prediction of saturated water density (temperature-dependent corrected model).
Figure 2 compares the ability of the original and modified forms of the
Peng-Robinson equation to describe the saturated vapor and liquid densi-
ties of nitrogen. It is evident that the correction term provides an improved
description in the vicinity of the critical point. Figure 3 is an analogous plot
for water. Figures 2 and 3 both indicate that description of the saturated
liquid density has some inadequacy. This weakness may be removed by
making the parameter s temperature dependent. In the case of water, for
example, if we assume temperature dependence as follows,
s = - 5.26 + 1201/T (15)
(where T is the temperature in kelvin), the average absolute error in the
saturated liquid density is reduced from 1.7% (Table 2) to 0.2%. The results
with a temperature-dependent s are presented in Fig. 4. We have found the
extended temperature dependence to be important for applications where
extremely accurate liquid densities are required (e.g., the correlation of
surface tension using the Macleod-Sudgen method; Reid et al., 1987, p.
633).
Figure 5 shows the corrected Peng-Robinson equation for the critical
isotherm of water. The corrected equation, by definition, reproduces the
critical density. It also improves the description of the extreme flatness in
the vicinity of the critical point.

9. 85
NBS-NRC Steam Tables (1984)
Penq-Robinson.' ___ ____________________
Corrected Peng-Robinson
0+i -/-
0.6 0.8 1 1.2 1.4 1.6
Reduced Pressure
Fig. 5. Prediction of water density along the critical isotherm.
1.
i
0 Friedman et al. (1965)
0 Mikhail et al. (1969)
Peng-Robinson------
Co Peng-Robinson wth Correction
".
c.
(0
0.6 ~ 1-77 ._I
0 0.2 0.4 0.6 0.8 1
Mole Fraction of Methanol
Fig. 6. Prediction of methanol-water liquid density (temperature, 25 o C; pressure, 1 atm).

10. 86
The simple mixing rules proposed in equations (11) and (12) allow good
description of molar volumes of mixtures. Figure 6 shows that reasonable
results are obtained for the methanol-water data of Friedman and Sherage
(1965) and Mikhail and Rime1 (1969).
CONCLUSIONS
The correction term described by eqn. (7) provides a simple and reliable
way to improve the liquid densities predicted by the Peng-Robinson equa-
tion of state. The correction also provides a slight improvement in vapor
densities. This approach is also applicable to other equations of state. The
model contains one adjustable parameter for each substance but its value
can be determined from a single low-temperature liquid density, say at the
normal boiling point.
Although it is possible to use an analogous procedure to improve other
thermodynamic properties, notably the enthalpy departure, we do not re-
commend it, because to do so would result in a loss of the internal
consistency between fugacity and enthalpy departure, which is inherent in
equations of state. For example, this internal consistency ensures good
predictions of low reduced-temperature heats of vaporization in spite of the
poor PVT predictions of eqn. (1). Such difficulties with empirical correc-
tions for properties like the enthalpy departure illustrate the strong need for
fundamentally improved models that can provide good predictions for all
thermodynamic properties.
LIST OF SYMBOLS
a, b
B corr
Cl, c2, c3
P
PC
R
s
T
T,
TR
u
0,
V
con-
Peng-Robinson parameters, eqn. (1)
shift in second virial coefficient, eqn. (14)
vapor pressure correlation constants, eqn. (5)
pressure
critical pressure
gas constant
molar volume correction term (cc gmol-I)
temperature
critical temperature
reduced temperature (T/T,)
Peng-Robinson molar volume (cc gmol-l), eqn. (1)
critical volume (cc gmol-l)
corrected Peng-Robinson molar volume (cc gmol-‘), eqn. (7)

11. 87
Greek letters
bulk modulus, eqn. (8)
temperature dependence of Peng-Robinson parameter a, eqn.
(3)
REFERENCES
Ely, J.F., 1985. Prediction of the thermophysical properties of mixtures of carbon dioxide and
light hydrocarbons. Computer Program DDMIX, National Bureau of Standards, (U.S.),
technical note to be published.
Ely, J.F., Magee, J.W. and Haynes, W.M., 1985. Thermophysical properties of carbon dioxide
at temperatures from 216 to 1000 K with pressures to 1000 bar, National Bureau of
Standards, (U.S.), monograph to be published.
Friedman, M.E. and Sheraga, H.A., 1965. J. Phys. Chem., 69: 3795-3800.
Fuller, G.G., 1976. Ind. Eng. Chem. Fundam., 15: 254-257.
Goodwin, R.D., 1974a. Provisional values for the thermodynamics functions of ethane.
National Bureau of Standards, (U.S.), NBSIR: 74-398.
Goodwin, R.D., 1974b. The thermodynamic properties of methane. National Bureau of
Standards, (U.S.), Tech. Note 653.
Goodwin, R.D., 1977. The thermodynamic properties of propane. National Bureau of
Standards, (U.S.), NBSIR: 77-860.
Goodwin, R.D., 1979. Provisional values for the thermodynamic functions of n-butane.
National Bureau of Standards, (U.S.), NBSIR: 79-1691.
Goodwin, R.D. and Haynes, W.M., 1982. The thermodynamic properties of isobutane.
National Bureau of Standards, (U.S.), Tech. Note 1051.
Haar, L., Gallagher, J.S. and Kell, G.S., 1984. NBS/NRC Steam Tables. Thermodynamic
and transport properties and computer programs for vapor and liquid states of water in SI
units, Hemisphere Publishing Company, Washington, D.C.
Henderson, O., 1979. Equations of state in research and engineering, Chao K.C. and
Robinson Jr., R.L., (Eds.), Advances in Chemistry Series 182, American Chemical Society.
Washington, D.C. p. l-30.
Jacobsen, R.T., Stewart, R.B., McCarty, R.D. and Hanley, H.J.M., 1973. Thermophysical
properties of nitrogen. National Bureau of Standards, (U.S.), Technical Note 648.
Martin, J.J., 1979. Ind. Eng. Chem. Fundam., 18: 81-97.
Mathias, P.M. and Copeman, T.W., 1983. Fluid Phase Equilibria, 13: 91-108.
M&hail, S.Z. and Kimel, W.R., 1969. J. Chem. Eng. Data. 6: 533-537.
Morris, R.W. and Turek, E.A., 1986. ACS Symp. Ser., 300: 389.
Patel, N.C. and Teja, A.S., 1982. Chem Eng. Sci., 37: 463-473.
Peneloux, A. and Rauzy, E., 1982. Fluid Phase Equilibria, 8: 7-23.
Peng, D.Y. and Robinson, D.B., 1976. Ind. Eng. Chem. Fundam., 15: 59-64.
Reid, R.C., Prausnitz, J.M. and Poling, B.E., 1987. The properties of gases and liquids, 4th
Edn., McGraw-Hill, New York.
Schmidt, G. and Wenzel, H., 1980. Chem Eng. Sci., 15: 1503.
Soave, G., 1972. Chem. Eng. Sci., 27: 1197-1203.
Trebble, M.A. and Bishnoi, P.R., 1986. Fluid Phase Equilibria, 29: 465-474.
Yarborough, L., 1979. Adv. Chem. Ser., 182: 385.