Embed presentation
Download to read offline
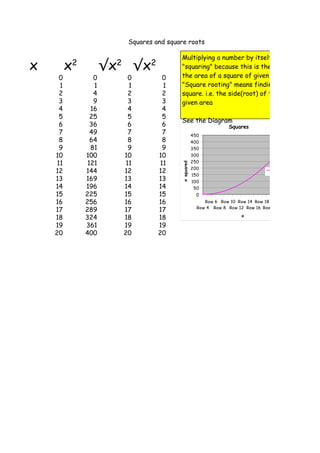




The document shows a table with numbers from 0 to 20 in the x column. The x2 column contains the square of each number in the x column. Taking the square root of each number in the x2 column results in the original number from the x column. Squaring a number is calculating the area of a square with that number as its side length. Taking the square root means finding the side length of a square with the given area.



