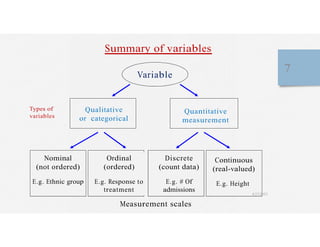
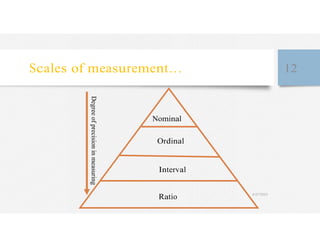
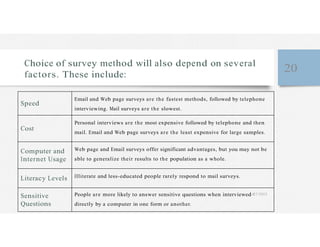
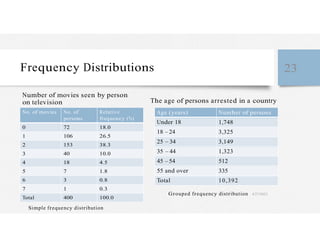
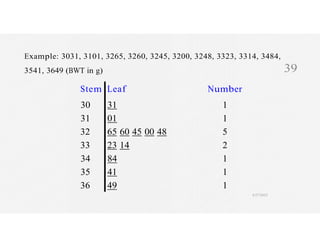
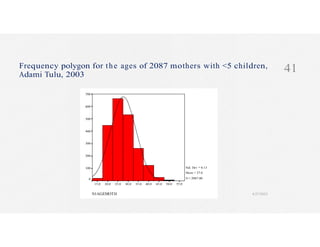
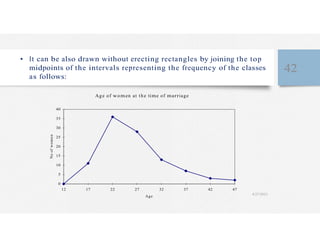
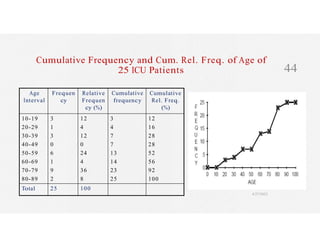
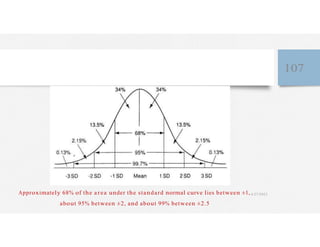
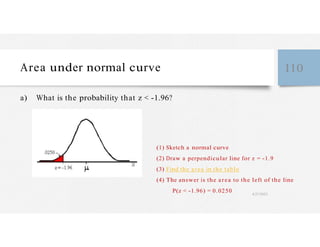
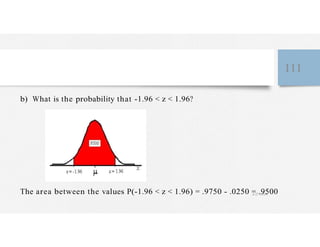
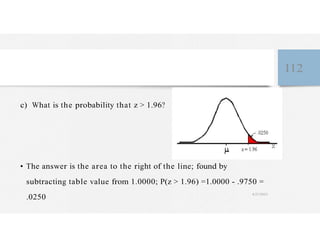
This document discusses variables and data collection methods in statistics and biostatistics. It defines key terms like variables, scales of measurement, and types of data collection. It explains that variables can be categorical or quantitative, and quantitative variables can be discrete or continuous. The scales of measurement from nominal to ratio are described. Common data collection methods include observation, questionnaires, interviews, and using documentary sources. Factors to consider when choosing a data collection method include speed, cost, literacy levels, and sensitivity of questions. Frequency distributions and grouped frequency distributions are introduced as ways to organize and present data.
















































































































![Non-probability sampling methods 145
• Every element in the universe [sampling frame] does not have equal
probability of being chosen in the sample.
a) Convenience sampling
– Drawn at the convenience of the researcher. Common in exploratory research.
– Does not lead to any conclusion
b) Judgmental sampling
– Sampling based on some judgment, gut-feelings or experience of the researcher.
– If inference drawing is not necessary, these samples are quite useful.
4/27/2023](https://image.slidesharecdn.com/4-230523232306-c40ad955/85/4-1-Handling-data-conv-docx-146-320.jpg)
