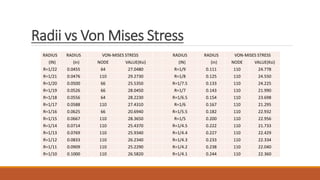
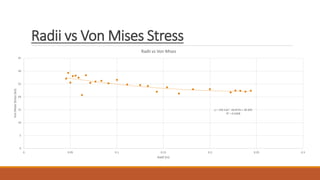
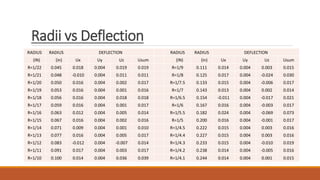
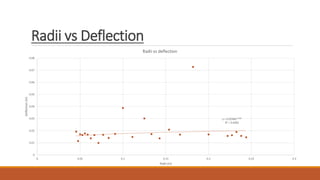
1) The document presents the results of a 3D structural analysis and optimization of a variable cross-section steel plate fixed at the top end and carrying a 1500 lb load at the bottom. 2) The analysis examined the relationship between fillet radii and deflection/von misses stress in the plate. 3) The results show relationships between fillet radii and von mises stress and deflection, with R-squared values indicating a moderate fit. Areas for improving the model are identified.

1. 3D - Structural Analysis
and Optimization
By Suresh Darvath

2. Problem Statement
Variable cross section steel plate
Fixed at the top end
Carries a load of 1500 lb at bottom
Aim: To find the relationship between the fillet radii and deflection/von misses stress
Validation:
Safety factor of 1.5 is chosen
Yield stress of steel is 36 Psi
Therefore the max. stress is 24 Psi

3. Batch file
/UNITS,bin
/filname,3D Structural Analysis and
Optimization
/title,3D Structural Analysis and Optimization
R_=0.25 !Radius of the Fillet
T_=0.125 !Thickness of the Model
/prep7
! MATERIAL PROPERTIES
ET,1,Plane82 !2-D 8-Node Structural Solid
ET,2,SOLID45 ! 3-D 8-Node Structural Solid
MP,EX,1,29e6 !define material properties
MP,PRXY,1,0.3
L,1,2
L,2,6
L,6,5
L,5,8
L,8,7
L,7,3
L,3,4
L,4,1
!Fillet Radius (Arbitary
Value is 0.125 inch)
LFILLT,3,4,R_ !line 9
LFILLT,4,5,R_ !line 10
AL,1,2,3,9,4,10,5,6,7,8
TYPE,1
MAT,1
LESIZE,1,,,10
LESIZE,2,,,13
LESIZE,3,,,5
LESIZE,9,,,5
LESIZE,4,,,20
LESIZE,10,,,5
LESIZE,5,,,5
LESIZE,6,,,13
LESIZE,7,,,5
LESIZE,8,,,40
AMESH,1
SAVE
! define the keypoint
K,1,0,0,0
K,2,2,0,0
K,3,2,-10,0
K,4,1,-10,0
K,5,1.75,-2.5,0
K,6,2,-2.5,0
K,7,2,-7.5,0
K,8,1.75,-7.5,0

4. Batch file
!Extrude the 2-D model into 3-D
model
TYPE,2
MAT,1
EXTOPT,esize,4
EXTOPT,aclear,all
K,20,0,0,T_
L,1,20
EXTOPT,esize,1,1
EXTOPT,aclear,all
VDRAG,all,,,,,,11
SAVE
FINISH
/SOLUTION
ANTYPE,STATIC,NEW
! Applying boundary conditions
(displacements)
NSEL,S,LOC,Y,0
D,all,UY,0
NSEL,ALL
!Apply load
NSEL,S,LOC,Y,-10
SF,ALL,PRES,750/T_
NSEL,ALL
SOLVE
FINISH
!GENERAL POSTPROCESSOR
/POST1
ETABLE,AxiStres,LS, 1,4
ETABLE,MaxStres,NMISC, 1,3
ETABLE,MinStres,NMISC,2,4
ETABLE,XForce,SMISC,1,7
ETABLE,YForce,SMISC,2,8
ETABLE,MOMENT, SMISC,6,12
PRETAB,AXISTRES,MAXSTRES,MINSTRES,
XFORCE,YFORCE,MOMENT
/EOF

5. Radii vs Von Mises Stress
RADIUS RADIUS VON-MISES STRESS RADIUS RADIUS VON-MISES STRESS
(IN) (in) NODE VALUE(Ksi) (IN) (in) NODE VALUE(Ksi)
R=1/22 0.0455 64 27.0480 R=1/9 0.111 110 24.778
R=1/21 0.0476 110 29.2730 R=1/8 0.125 110 24.550
R=1/20 0.0500 66 25.5350 R=1/7.5 0.133 110 24.225
R=1/19 0.0526 66 28.0450 R=1/7 0.143 110 21.990
R=1/18 0.0556 64 28.2230 R=1/6.5 0.154 110 23.698
R=1/17 0.0588 110 27.4310 R=1/6 0.167 110 21.295
R=1/16 0.0625 66 20.6940 R=1/5.5 0.182 110 22.932
R=1/15 0.0667 110 28.3650 R=1/5 0.200 110 22.956
R=1/14 0.0714 110 25.4370 R=1/4.5 0.222 110 21.733
R=1/13 0.0769 110 25.9340 R=1/4.4 0.227 110 22.429
R=1/12 0.0833 110 26.2340 R=1/4.3 0.233 110 22.334
R=1/11 0.0909 110 25.2290 R=1/4.2 0.238 110 22.040
R=1/10 0.1000 110 26.5820 R=1/4.1 0.244 110 22.360

6. Radii vs Von Mises Stress
y = 139.13x2 - 66.872x + 30.205
R² = 0.6208
0
5
10
15
20
25
30
35
0 0.05 0.1 0.15 0.2 0.25 0.3
VonMisesStress(ksi)
Radii (in)
Radii vs Von Mises

7. Radii vs Deflection
RADIUS RADIUS DEFLECTION RADIUS RADIUS DEFLECTION
(IN) (in) Ux Uy Uz Usum (IN) (in) Ux Uy Uz Usum
R=1/22 0.045 0.018 0.004 0.019 0.019 R=1/9 0.111 0.014 0.004 0.003 0.015
R=1/21 0.048 -0.010 0.004 0.011 0.011 R=1/8 0.125 0.017 0.004 -0.024 0.030
R=1/20 0.050 0.016 0.004 0.002 0.017 R=1/7.5 0.133 0.015 0.004 -0.006 0.017
R=1/19 0.053 0.016 0.004 0.001 0.016 R=1/7 0.143 0.013 0.004 0.002 0.014
R=1/18 0.056 0.016 0.004 0.018 0.018 R=1/6.5 0.154 -0.011 0.004 -0.017 0.021
R=1/17 0.059 0.016 0.004 0.001 0.017 R=1/6 0.167 0.016 0.004 -0.003 0.017
R=1/16 0.063 0.012 0.004 0.005 0.014 R=1/5.5 0.182 0.024 0.004 -0.069 0.073
R=1/15 0.067 0.016 0.004 0.002 0.016 R=1/5 0.200 0.016 0.004 -0.001 0.017
R=1/14 0.071 0.009 0.004 0.001 0.010 R=1/4.5 0.222 0.015 0.004 0.003 0.016
R=1/13 0.077 0.016 0.004 0.005 0.017 R=1/4.4 0.227 0.015 0.004 0.003 0.016
R=1/12 0.083 -0.012 0.004 -0.007 0.014 R=1/4.3 0.233 0.015 0.004 -0.010 0.019
R=1/11 0.091 0.017 0.004 0.003 0.017 R=1/4.2 0.238 0.014 0.004 -0.005 0.016
R=1/10 0.100 0.014 0.004 0.036 0.039 R=1/4.1 0.244 0.014 0.004 0.001 0.015

8. Radii vs Deflection
y = 0.0248x0.1481
R² = 0.0482
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0 0.05 0.1 0.15 0.2 0.25 0.3
Deflection(in)
Radii (in)
Radii vs deflection

9. Mesh Scene

11. Plan Moving Forward
From the above trails, we have come up with
•The R - relevance number of 0.62 is not reasonable
•Adding more number of elements in thickness of the model
•Controlling the minimum number of elements on the radii through smart size
•Improving the mesh by having more number of elements
•Understand the behavior for radii values where the results are not good