Учебное пособие охватывает вычислительные методы, используемые для решения инженерных и научно-технических задач, включая линейную алгебру, нелинейные уравнения, численное интегрирование и дифференцирование. Книга предназначена для студентов и аспирантов технических вузов, а также инженеров и научных работников, содержащая примеры, иллюстрации и обсуждения методов, алгоритмов и их реализации на компьютере. Второе издание включает исправления и новые темы, основанные на опыте преподавания и актуальных методах вычислений.

2. А. А. АМОСОВ,
Ю. А. ДУБИНСКИЙ,
Н.В.КОПЧЕНОВА
ВЬIЧИСЛИТЕЛЬНЬIЕ
МЕТОДЬI
Учебное пособие
Издание четвертое, стереотипное
ьСАНКТ-ПЕТЕРБУРГ· МОСКВА· КРАСНОДАР
2014

3. ББК22.1я73
А62
Амосов А. А., Дубинский Ю. А., Копченова Н. В.
А 62 Вычислительные методы: Учебное пособие. - 4-е
изд., стер. - СПб.: Издательство (<Ланы, 2014. -
672 с.: ил. - (Учебники для вузов. Специальная литера­
тура).
ISBN 978-5-8114-1623-3
В книге рассматриваются вычислительные методы, наиболее
часто используемые в практике прикладных и научно-технических
расчетов: методы решения задач линейной алгебры, нелинейных
уравнений, проблемы собственных значений, методы теории
приближения функций, численное дифференцирование и интегри­
рование, поиск экстремумов функций, решение обыкновенных диф­
ференциальных уравнений, численное решение интегральных
уравнений, линейная и нелинейная задачи метода наименьших
квадратов, метод сопряженных градиентов. Значительное внимание
уделяется особенностям реализации вычислительных алгоритмов на
компьютере и оценке достоверности полученных результатов. Имеет­
ся большое количество примеров и геометрических иллюстраций.
Даются сведения о стандарте IEEE, о сингулярном разложении
матрицы и его применении для решения переопределенных систем, о
двухслойных итерационных методах, о квадратурных формулах
Гаусса-Кронрода, о методах Рунге-Кутты-Фельберга.
Учебное пособие предназначено для студентов всех направлений
подготовки, обучающихся в классических и технических универ­
ситетах и изучающих вычислительные методы, будет полезно аспи­
рантам, инженерам и научным работникам, применяющим вычисли­
тельные методы в своих исследованиях.
ББК 22.1я73
Рецензенты:
Н. Н. КАЛИТКИН - член-корреспондент РАН;
Н. С. БАХВАЛОВ - профессор, зав. кафедрой вычислительной
математики механико-математического факультета МГУ, академик
РАН;
Е. И. МОИСЕЕВ - профессор, декан факультета вычислительной
математики и кибернетики МГУ, член-корреспондент РАН.
Обложка
Е. А. ВЛАСОВА
© Издательство •Ланы, 2014
© Коллектив авторов, 2014
© Издательство •Лавы,
художественное оформление, 2014

4. Цель расчетов - не числа, а понимание.
Р.В. Хемминг
Из нашего девиза «Цель расчетов - не
числа, а понимание» следует, что человек,
который должен этого понимания достиг­
нуть, обязан знать, как происходит вычис­
ление. Если он не понимает, что делается,
то очень маловероятно, чтобы он извлек из
вычислений что-нибудь ценное. Он видит
голые цифры, но их истинное значение мо­
жет оказаться скрытым в вычислениях.
Р.В. Хемминг
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
В настоящее время имеется значительное число учебников и моно­
графий, посвященных методам вычислений (часть из них отражена в
списке литературы к данному пособию). Однако, на наш взгляд, боль­
шинство этих книг ориентировано на студентов-математиков или на
специалистов по вычислительной математике. В то же время практиче­
ски отсутствует отечественная учебная литература, в которой доступ­
ным для студента технического вуза или инженера образом были бы
изложены основы вычислительных методов, применяемых сегодня для
решения инженерных задач. Особенно острой, по мнению авторов,
является потребность в книге, которая содержала бы не только изложе­
ние начал численных методов, но и давала бы представление о реально
используемых в вычислительной практике алгоритмах. Данное учебное
пособие призвано в определенной степени восполнить этот пробел.
Настоящее пособие адресовано в первую очередь студентам и аспи­
рантам высших технических учебных заведений, изучающим основы
математического моделирования и численные методы. Авторы наде­
ются на то, что эта книга будет полезна широкому кругу инженерных и
научно-технических работников, которые намерены применять ЭВМ
для решения прикладных задач.
При написании книги авторы использовали многолетний опыт пре­
подавания курса вычислительных методов студентам и аспирантам
различных специальностей Московского энергетического института, а
также опыт работы в вычислительном центре МЭИ. Значительное
влияние на выбор материала и характер изложения оказали также мно­
гочисленные дискуссии со слушателями существующего при МЭИ
факультета повышения квалификации преподавателей вузов страны.
Авторы стремились изложить материал по возможности наиболее
простым и доступным образом. Объем знаний высшей математики,
необходимый для понимания содержания книги, не выходит за рамки
программы младших курсов втуза. Пособие содержит довольно много
3

5. Предисловие
примеров, иллюстрирующих те или иные положения теории, а также
демонстрирующих особенности вычислительных методов или работу
конкретных алгоритмов. Тем не менее, многие из рассматриваемых
вопросов трудны для восприятия и требуют внимательного изучения. К
сожалению, в учебной литературе они нередко опускаются. К таким цен­
тральным вопросам относятся, например понятия корректности, устойчи­
вости и обусловленности вычислительных задач и вычислительных алго­
ритмов, особенности поведения вычислительной погрешности. Важность
их понимания для эффективного применения ЭВМ сегодня велика и не
акцентировать на них внимание авторы посчитали невозможным.
Дадим краткое изложение основного содержания книги. Важную идей­
ную нагрузку несут на себе первые три главы. Рассматриваемые в них
вопросы закладывают фундамент, необходимый для правильного пони­
мания изложенных в остальных главах вычислительных методов.
В гл. 1 дается общее представление о методе математического моде­
лирования, в том числе о процессе создания математических моделей,
последовательности этапов решения инженерной задачи с применение
ЭВМ, вычислительном эксперименте.
В гл. 2 наряду с введением в элементарную теорию погрешностей
содержится изложение основных особенностей машинной арифметики.
Понимание этих особенностей необходимо тем, кто заинтересован в
эффективном применении ЭВМ для решения прикладных задач.
В гл. 3 обсуждаются важнейшие свойства вычислительных задач,
методов и алгоритмов. Дается общее представление о корректности,
устойчивости и обусловленности вычислительной задачи. Приводится
описание основных классов вычислительных методов. Значительное
внимание уделяется устойчивости вычислительных алгоритмов, их чув­
ствительности к ошибкам. Дается представление о различных подходах к
анализу ошибок, в том числе и об обратном анализе ошибок. Обсужда­
ются требования, предъявляемые к вычислительным алгоритмам.
Конкретные вычислительные задачи и методы их решения рассмат­
риваются начиная с гл. 4. Здесь авторы стремились к тому, чтобы не
только изложить простейшие подходы, но и дать представление об
алгоритмах, которые реально используются для решения соответствую­
щих задач.
В гл. 4 рассматриваются методы отыскания решений нелинейных
уравнений. Значительное внимание уделено постановке задачи и ее
свойствам, в частности - чувствительности корней нелинейных урав­
нений к погрешностям. Среди различных методов отыскания корней
более подробно излагаются метод простой итерации, метод Ньютона и
различные их модификации.
В гл. 5 рассмотрены прямые (точные) методы решения систем
линейных алгебраических уравнений. Основное внимание уделяется
4

6. Предисловие
методу Гаусса и его различным модификациям. Рассматриваются
использование LИ-разложения матриц для решения систем линейных
уравнений, метод квадратных корней, метод прогонки, методы враще­
ний и отражений. Обсуждается алгоритм итерационного уточнения.
В гл. 6 рассматриваются итерационные методы решения систем
линейных алгебраических уравнений: метод простой итерации, метод
Зейделя, метод релаксации и другие методы.
В гл. 7 рассматривается задача отыскания решений систем нелинейных
уравнений. Обсуждаются не только соответствующие итерационные
методы, но и различные подходы к решению сложной задачи локализации.
В гл. 8 дается представление о проблеме собственных значений
и о различных подходах к вычислению собственных значений и собст­
венных векторов. Излагаются степенной метод и обратный степенной
метод, обсуждается QR-алгоритм.
В гл. 9 излагаются наиболее известные численные методы решения
задачи одномерной минимизации, в том числе метод деления отрезка
пополам, метод Фибоначчи, метод золотого сечения и метод Ньютона.
В гл. 10 рассматриваются различные методы решения задачи безус­
ловной минимизации. Наиболее полно изложены градиентный метод,
метод Ньютона и метод сопряженных градиентов.
В гл. 11 рассмотрены наиболее важные и часто встречающиеся
в приложениях методы приближения функций. Значительное внимание
уделено интерполяции, причем рассматривается интерполяция не только
алгебраическими многочленами, но и тригонометрическими многочле­
нами, а также интерполяция сплайнами. Достаточно подробно обсужда­
ется метод наименьших квадратов. Дается понятие о наилучшем равно­
мерном приближении и дробно-рациональных аппроксимациях.
В эту главу включены также некоторые вопросы, имеющие непо­
средственное отношение к методам приближения функций. Это конеч­
ные и разделенные разности, многочлены Чебышева, быстрое дискрет­
ное преобразование Фурье.
В гл. 12 рассматриваются различные подходы к выводу формул чис­
ленного дифференцирования, обсуждается чувствительность этих фор­
мул к ошибкам в вычислении значений функции.
В гл. 13 излагаются методы вычисления определенных интегралов.
Выводятся квадратурные формулы интерполяционного типа и квадра­
турные формулы Гаусса. Дается представление о принципах построения
адаптивных процедур численного интегрирования и, в частности, об
используемых в них способах апостериорной оценки погрешности. Рас­
сматриваются различные подходы к вычислению интегралов от функ­
ций, имеющих те или иные особенности. В частности, затрагивается
проблема интегрирования быстро осциллирующих функций.
5

7. Предисловие
Глава 14 посвящена численным методам решения задачи Коши для
обыкновенных дифференциальных уравнений. Подробно рассматрива­
ются метод Эйлера и его различные модификации. Значительное вни­
мание уделено рассмотрению классических методов Рунге-Кутты
и Адамса. Обсуждаются различные свойства устойчивости численных
методов решения задачи Коши, в том числе нуль-устойчивость, абсо­
лютная устойчивость, А-устойчивость, А(а)-устойчивость. Специально
рассматриваются жесткие задачи и методы их решения.
В гл. 15 изучаются методы численного решения двухточечных крае­
вых задач. Подробно излагается применение метода конечных разно­
стей к решению краевых задач для обыкновенного дифференциального
уравнения второго порядка. Дается представление о проекционных
методах Ритца и Галеркина; обсуждается один из их современных
вариантов - метод конечных элементов. Завершает главу рассмотре­
ние метода пристрелки.
Можно предположить, что к изучению отдельных параграфов или
даже глав этой книги читатель приступит, только столкнувшись с необ­
ходимостью решить на ЭВМ важную для него задачу. Вероятно, в этом
случае польза от изучения соответствующего раздела будет наиболь­
шей. Многие вопросы рассмотрены очень кратко или не рассмотрены
вообще. Авторы надеются на то, что соответствующие пробелы можно
восполнить, использовав сделанные в тексте ссылки на известные
учебники и монографии.
В ряде случаев авторы позволяют себе интерпретировать те или иные
результаты, делать определенные выводы и даже давать рекомендации
в надежде на то, что для новичка соответствующие рассуждения дадут
полезный начальный ориентир. В целом же ко всяким рекомендациям
в такой сложной и многообразной области, как применение вычислитель­
ных методов для решения прикладных задач на ЭВМ, следует отнестись
с осторожностью. Они не могут претендовать на бесспорность и их сле­
дует рассматривать скорее как отражение точки зрения авторов.
Иногда то или иное положение обосновывается ссылкой на вычис­
лительную практику. Хотя критерий практики и играет при отборе
методов вычислений существенную роль, все же оценки методов, осно­
ванные на результатах их применения для решения конкретных задач,
нередко бывают весьма субъективны и противоречивы.
В заключение отметим, что никакие теоретические положения и
советы не могут заменить собственного опыта вычислительной работы.
Как надеются авторы, параллельно с изучением данной книги такой
опыт может приобрести читатель, переходя от решения задач учебного
характера к серьезным практическим задачам.
Авторы
6

8. ПРЕдИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Со времени выхода в свет первого издания этой книги, в 1994 г.
в издательстве «Высшая школа>>, прошло около десяти лет. За это время
стало ясно, что она нашла своего читателя. Книга активно используется
студентами, аспирантами, преподавателями и научными сотрудниками
не только Московского энергетического института, но и других вузов
страны. В то же время обнаружился ряд опечаток и неточностей в из­
ложении, которые было бы желательно исправить. Поэтому авторы с
благодарностью приняли любезное предложение Издательства МЭИ о
переиздании учебного пособия.
Во втором издании книги исправлены замеченные недостатки. Рас­
смотрен ряд вопросов, которые не были включены в первое издание.
Это стандарт IEEE, сингулярное разложение матрицы и его примене­
ние для решения переопределенных систем, двухслойные итерацион­
ные методы решения систем линейных алгебраических уравнений
(включая метод с чебышевским набором параметров, метод сопряжен­
ных градиентов и предобусловливание), обратная интерполяция, интер­
поляционный многочлен Бесселя, многомерная интерполяция, квадра­
турные формулы Гаусса-Кронрода, метод Рунге-Кутты-Фельберга.
Дополнен список литературы.
Авторы пользуются случаем выразить свою благодарность россий­
ским ученым, которые оказали существенное влияние на формирование
их взглядов на вычислительную математику. Это акад. РАН Н.С. Бах­
валов, акад. РАН В.В. Воеводин, акад. РАН А.А. Самарский, акад. РАН
А.Н. Тихонов, проф. Ф.П. Васильев, проф. Е.Г. Дьяконов, проф. Я.М. Жи­
лейкин, проф. Х.Д. Икрамов, проф. Г.М. Кобельков, докт физ-мат. наук
А.С. Кронрод, проф. И.А. Марон.
Работа по подготовке второго издания к печати выполнена проф.
А.А. Амосовым. Авторы искренне признательны своим коллегам проф.
А.А. Злотнику, доц. О.А. Амосовой и доц В.П. Григорьеву, чьи заме­
чания были существенно использованы в процессе работы над вто­
рым изданием. Авторы заранее благодарны всем, кто пожелает вы­
сказать свои замечания и предложения. Их следует направлять по ад­
ресу: 111250, Москва, Красноказарменная ул., д. 14, Издательство
МЭИ или по адресу AmosovAA@mpel.ru.
Авторы
7

9. ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Перед Вами третье издание книги, которая теперь называется «Вычис­
лительные методы», хотя в двух предыдущих изданиях она выходила под
названием «Вычислительные методы для инженеров». По-видимому,
авторы должны как-то объяснить, почему название книги стало сущест­
венно короче.
Во-первых, методы вычислений, применяемые для решения возни­
кающих на практике задач, универсальны. И не существует каких-то специ­
альных методов, предназначенных для решения только лишь инженерных
задач. Поэтому изложенные в книге методы могут использоваться студен­
тами, аспирантами и исследователями для решения самых разных задач, в
том числе - экономических, медицинских, биологических и т.д. Нет необхо­
димости специально сужать круг возможных читателей.
Во-вторых, перемены, происходящие в высшем образовании нашей
страны, скоро приведут к тому, что высокое звание «инженер» станет воспри­
ним~rгься как архаика. Книга, предназначенная для каких-то непонятных инже­
неров, может показ~rгься ненужной будущим бакалаврам и магистрам. Так что
сокращение названия книги - это и вынужденная дань нынешней моде.
Чем это издание отличается от предыдущего? Во-первых, в нем исправ­
лены обнаруженные неточности и опечатки. Во-вторых, добавлена новая глава,
посвященная численному решению интегральных уравнений. В третьих, час­
тично изменено содержание некоторых параграфов. Существенной перера­
ботке подвергся параграф 2.5, посвященный особенностям машинной
арифметики. В нем теперь достаточно полно отражены особенности IEEE
арифметики, реализованной в настоящее время на большинстве современ­
ных компьютеров. Достойное место в книге, наконец, занял метод наимень­
ших квадратов. В ней появились два новых параграфа, посвященных
линейной и нелинейной задачам метода наименьших квадратов. Появился
также отдельный параграф, посвященный методу сопряженных градиентов
решения систем линейных алгебраических уравнений.
Список литературы дополнен. Ссылки на литературу, добавленную к
третьему изданию, помечены звездочкой.
Работа по подготовке к печати третьего издания выполнена проф.
А.А. Амосовым.
Авторы заранее благодарны читателям, которые пожелают высказать
свои замечания или предложения по содержанию книги. Их следует
направлять по адресу 111250, Москва, Красноказарменная ул., д. 14, Изда­
тельский дом МЭИ или по адресу электронной почты AmosovAA@mpei.ru.
Авторы
8

10. Глава 1
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
И РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ
С ПРИМЕНЕНИЕМ КОМПЬЮТЕРА
В этой главе дается общее представление о методе математического
моделирования, в том числе о процессе создания математических моде­
лей, о последовательности этапов решения прикладной задачи с приме­
нением компьютера, о вычислительном эксперименте.
Разделение решаемых с применением компьютера задач на приклад­
ные и научные является до известной степени условным. Тем не менее,
при написании данного пособия авторы ориентировались на читателя,
интересующегося решением именно прикладных задач. Попытаемся
охарактеризовать этот класс задач, выделив его некоторые характерные
особенности.
1. Прикладные задачи имеют ярко выраженную практическую
направленность. Целью их решения является создание новой конструк­
ции, разработка нового технологического процесса, минимизация затрат
на производство некоторого изделия и т.д. Поэтому для таких задач
характерна необходимость доведения результатов до конкретных чисел,
графиков, таблиц, на основании которых можно принимать решения.
2. Эти задачи характеризуются значительным объемом выполняе­
мой вычислительной работы.
3. Для этих задач характерно использование достаточно сложных
математических моделей и серьезного математического аппарата.
4. Прикладные задачи, как правило, решают специалисты, не являю­
щиеся профессионалами в области разработки математических мето­
дов и программного обеспечения компьютеров. Поэтому естественно
желание этих специалистов использовать готовые вычислительные
методы и стандартное математическое программное обеспечение.
Наконец, условимся считать, что в рассматриваемый класс задач
входят задачи только умеренной сложности. Для их решения не требу­
ются сверхбольшие скорости вычислений и сверхбольшие объемы
памяти для хранения данных. Таким образом, эти задачи могут быть
решены с помощью компьютеров, доступных массовому пользователю.
Те же задачи, которые требуют для решения сверхмощной вычисли­
тельной техники и принципиально новых алгоритмов, будем относить
к категории научных задач.
9

11. Глава 1. Математическое моделирование и решение прикладных задач
§ 1.1. Математическое моделирование
и процесс создания математической модели
Математическое .моделирование представляет собой метод иссле­
дования объектов и процессов реального мира с помощью их прибли­
женных описаний на языке математики - математических моделей.
Этот метод чрезвычайно плодотворен и известен уже несколько тыся­
челетий. Насущные задачи земледелия и строительства еще в древние
времена приводили к необходимости определения площадей и объе­
мов, а следовательно, и к рассмотрению элементарных геометрических
фигур, дающих пример простейших математических моделей. Возмож­
ности математического моделирования и его влияния на научно-техни­
ческий прогресс неизмеримо возросли в последние десятилетия в связи
с созданием и широким внедрением компьютеров.
Процесс создания математической модели условно можно разбить
на ряд основных этапов:
1) построение математической модели;
2) постановка, исследование и решение соответствующих вычисли-
тельных задач,
3) проверка качества модели на практике и модификация модели.
Рассмотрим основное содержание этих этапов.
1. Построение математической модели. Предполагается, что с
помощью наблюдений и экспериментов, практики (понимаемой в
самом широком смысле) получена достаточно подробная информация
об изучаемом явлении. Для рассматриваемого этапа характерно глубо­
кое проникновение в полученные факты в целях выяснения главных
закономерностей. Выявляются основные «характеристики)) явления,
которым сопоставляются некоторые величины. Как правило, эти вели­
чины принимают числовые значения, т.е. являются переменными, век­
торами, матрицами, функциями и т.д.
Установленным внутренним связям между «характеристиками))
явления придается форма равенств, неравенств, уравнений и логиче­
ских структур, связывающих величины, включенные в математическую
модель. Таким образом, математическая модель становится записью на
языке математики законов природы, управляющих протеканием иссле­
дуемого процесса или описывающих функционирование изучаемого
объекта. Она включает в себя набор некоторых величин и описание
характера связи между ними.
Построение математических моделей - существенная и очень важная
часть естественных и технических наук. Эта задача, требующая от иссле-
10

12. § 1.1. Математическое моделирование и процесс математической модели
дователя глубокоm знания предметной области, высокой матеfатической
культуры, опыта построения моделей, развитой интуиции и многого
друmго. Создание удачной новой модели - всегда крупное достижение
соответствующей науки, а иногда и целый этап в ее развитии.
Подчеркнем, что математическая модель неизбежно представляет
собой компромисс между бесконечной сложностью изучаемого явления
и желаемой простотой его описания. Модель должна быть достаточно
полной, для того чтобы оказаться полезной для изучения свойств иссле­
дуемого явления. В то же время она обязана быть достаточно простой,
для того чтобы допускать возможность ее анализа существующими в
математике средствами и ее реализации на компьютере. Из огромного
числа характеристик явления и действующих на него факторов требу­
ется выделить основные, определяющие, отбросив при этом второсте­
пенные, несущественные.
Нередко в математическую модель закладываются некоторые гипо­
те3Ы, еще не подтвержденные на практике. Такую математическую
модель часто называют гипотетической.
Приведем пример простейшей математической модели.
Пример 1.1. Пусть исследуется движение тела, брошенного со
скоростью v0 под утлом а к поверхности Земли.
Будем считать, что в рассматриваемом случае можно пренебречь
сопротивлением воздуха, считать Землю плоской, а ускорение свобод­
ного падения g - постоянной. Введем систему координат, ее начало
поместим в точку бросания, ось Ох направим горизонтально в направ­
лении бросания, а ось Оу - вертикально вверх (рис. 1.1 ). Пусть и(t) и
w(t) - горизонтальная и вертикальная составляющие скорости v(t) в
момент времени t (в начальный момент t = О, v = v0)
Согласно законам механики, при сделанных предположениях движе­
ние тела в горизонтальном направлении является равномерным, а в вер-
у
о
Рис. 1.1
11

13. Глава 1. Математическое моделирование и решение прикладных задач
тикальном - равноускоренным с ускорением, равным -g. Поэтому спра­
ведливы следующие равенства:
и= v0 cosa, х = (v0cosa)t, (1.1)
. gt2
w = v0 sina - gt, у= (v0 sшa)t- Т. (1.2)
Формулы (1.1 ), (1.2) и дают простейшую математическую модель
рассматриваемого явления, созданную в XVII в. Г. Галилеем 1. Заметим,
что при О < а < тс/2 траектория движения представляет собой параболу
у= - g х2 + (tga)x. .А.
2v~ cos2a
Математические модели часто разделяют на статические и динами­
ческие. Статическая модель описывает явление или ситуацию в пред­
положении их завершенности, неизменности (т.е. в статике). Динамиче­
ская модель описывает, как протекает явление или изменяется ситуация
от одного состояния к другому (т.е. в динамике). При использовании
динамических моделей, как правило, задают начальное состояние сис­
темы, а затем исследуют изменение этого состояния во времени.
2. Постановка, исследование и решение вычислительных задач.
Для того чтобы найти интересующие исследователя значения величин
или выяснить характер из зависимости от других входящих в математи­
ческую модель величин, ставят, а затем решают математические задачи.
Выявим основные типы решаемых задач. Для этого все величины,
включенные в математическую модель, условно разобьем на три группы:
1) исходные (входные) данные х;
2) параметры модели а;
3) искомое решение (выходные данные) у.
В динамических моделях искомое решение часто является функцией
времени у = y(t); переменная t в таких моделях, как правило, бывает
выделенной и играет особую роль.
Наиболее часто решают так называемые прямые задачи, постановка
которых выглядит следующим образом: по данному значению входного
данного х при фиксированных значениях параметров а требуется найти
решение у. Процесс решения прямой задачи можно рассматривать как
математическое моделирование причинно-следственной связи, прису­
щей явлению. Тогда входное данное х характеризует «причины» явле-
1 Галилео Галилей (1564-1642) - итальянский физик, механик, астроном, один из
основателей точного естествознания.
12

14. § 1.1. Математическое моделирование и процесс математической модели
ния, которые задаются и варьируются в процессе исследования, а иско­
мое решение у - «следствие».
Для того чтобы математическое описание было применимо не к еди­
ничному явлению, а к широкому кругу близких по природе явлений,
в действительности строят не единичную математическую модель, а неко­
торое параметрическое семейство моделей. Будем считать, что выбор
конкретной модели из этого семейства осуществляется фиксацией зна­
чений параметров модели а. Например, в роли таких параметров
могут выступать некоторые из коэффициентов, входящих в уравнения.
С помощью выбора параметров может производиться указание типа
функциональной зависимости между некоторыми из величин. Наконец,
если используемые математические модели разбиты на классы, то
параметром может служить и класс используемой модели.
Пр им ер 1.2. Для модели ( 1. 1), (1.2) прямую задачу естественно
формулировать как задачу вычисления величин и(t), w(t), x(t), y(t) по
задаваемым входным данным v0 , а. Параметром модели здесь является
ускорение свободного падения g. Его значение зависит от тоm, произ­
водится ли бросание тела с поверхности Земли на уровне Мировоm
океана, в глубокой шахте или же на большой высоте. Заметим, что та же
модель пригодна для описания движения тела, брошенноm на любой
другой планете, если значение параметра g для этой планеты известно. .&
Большую роль играет решение так называемых обратных задач,
состоящих в определении входного данного х по данному значению у
(параметры модели а, как и в прямой задаче, фиксированы). Решение
обратной задачи - это в определенном смысле попытка выяснить,
какие «причины» х привели к известному «следствию» у. Как правило,
обратные задачи оказываются сложнее для решения, чем прямые.
Пример 1.3. Для модели (1.1), (1.2) обратную задачу можно сфор­
мулировать так: по заданным и(t), w(t), x(t),y(t) требуется найти значе­
ния v0, а. Заметим, что для однозначного определения v0, а достаточно
задать в любой фиксированный момент t0 ~ О одну из пар величин
(и(t0), w(t0)) или (x(t0), y(t0)). .&
Помимо двух рассмотренных типов задач следует упомянуть еще
один тип - задачи идентификации. В широком смысле задача иденти­
фикации модели - это задача выбора среди множества всевозможных
моделей той, которая наилучшим образом описывает изучаемое явле­
ние. В такой постановке эта задача выглядит как практически неразре­
шимая проблема. Чаще задачу идентификации понимают в узком смысле,
как задачу выбора из заданного параметрического семейства моделей
13

15. Глава 1. Математическое моделирование и решение прикладных задач
конкретной математической модели (с помощью выбора ее параметров а),
с тем чтобы оптимальным в смысле некоторого критерия образом согла­
совать следствия из модели с результатами наблюдений.
Пример 1.4. Применительно к модели (1.1), (1.2) задача иденти­
фикации может состоять в определении значения ускорения свобод­
ного падения планеты g по результатам наблюдений за параметрами
траектории. А
Указанные три типа задач (прямые, обратные и задачи идентифика­
ции) будем называть вычислительными задачами. Для удобства изло­
жения в дальнейшем независимо от типа решаемой задачи будем назы­
вать набор подлежащих определению величин искомым решением
и обозначать через у, а набор заданных величин - входным данным
и обозначать через х.
Пример 1.5. При описании многих явлений используют модель
полиномиальной зависимости между величинами х и у:
у =Рп(х) = а0 + а1х + ". +апхп. (1.3)
Здесь а0 , а 1 , ... , ап - коэффициенты многочлена, являющиеся парамет­
рами модели (в число параметров модели можно включить и степень
многочлена).
При фиксированных значениях параметров прямая задача состоит
в вычислении значения многочлена у= Рп(х) по заданному х. В таком слу-
чае целью решения обратной задачи является определение по заданному
значению у соответствующего ему значения х. Нетрудно видеть, что это
есть задача отыскания корней многочлена, отличающегося от Р"(х) заме-
ной коэффициента а0 на а0 = а0 - у. Если же из практики известна неко­
торая информация о зависимости у от х, то определение параметров а0 ,
а1 , . .. ,ап, при которых модель (.3) наилучшим в некотором смысле обра­
зом описывает эту зависимость, представляет собой задачу идентифика­
ции. Например, если задана таблица значений х1 ,у1 (i = , ..., N), то такую
задачу в зависимости от ситуации можно решать, используя известные
методы интерполяции и наименьших квадратов (см. гл. 11). А
Пр им ер 1.6. Нередко входящие в модель функции x(t) и y(t)
бывают связаны равенством
1
y(t)=y0 + Jx(t)dt.
о
Например, так связаны между собой скорость x(t) и пуrь y(t) при
прямолинейном движении. Тогда при фиксированном значении пост~
14

16. § 1.1. Математическое моделирование и процесс математической модели
янной у0 прямая задача (задача интегрирования) состоит в вычислении
первообразной y(t) по заданной функции x(t). Обратная задача (задача
дифференцирования) заключается в вычислении x(t) = y'(t) по заданной
функции y{t).•
Как правило, решение вычислительной задачи не удается выразить
через входные данные в виде конечной формулы. Однако это совсем не
означает, что решение такой задачи не может быть найдено. Сущест­
вуют специальные методы, которые называют численными (или вычис­
лительными). Они позволяют свести получение численного значения
решения к последовательности арифметических операций над числен­
ными значениями входных данных. Эти методы были известны давно:
в качестве примера, уже ставшего классическим, можно привести
открытие Леверье 1 в 1846 г. новой планеты Нептун. Однако для реше­
ния задач численные методы применялись довольно редко, так как их
использование предполагает выполнение гигантского объема вычисле­
ний~ Поэтому в большйнстве случаев до появления компьютеров при­
ходилось избегать использования сложных математических моделей
и исследовать явления в простейших ситуациях, когда возможно найти
аналитическое решение. Несовершенство вычислительного аппарата
становилось фактором, сдерживающим широкое использование мате­
матических моделей в науке и технике.
Появление компьютеров кардинально изменило ситуацию. Класс
математических моделей, допускающих подробное исследование, резко
расширился. Решение многих, еще недавно недоступных, вычислитель­
ных задач стало обыденной реальностью.
3. Проверка качества модели на практике и модификация
модели. На этом этапе выясняют пригодность математической модели
для описания исследуемого явления. Теоретические выводы и конкрет­
ные результаты, вытекающие из гипотетической математической модели,
сопоставляют с экспериментальными данными. Если они противоречат
друг другу, то выбранная модель непригодна и ее следует пересмотреть,
вернувшись к первому этапу. Если же результаты совпадают с допусти­
мой для описания данного явления точностью, то модель можно при-
1 Урбен Жан Жозеф Леверье (1811-1877) - французский астроном. На основании
законов небесной механики, использовав данные об аномалиях в движении планеты Уран,
Леверье рассчитал траекторию движения гипотетической неизвестной планеты. В том же
году неtецкий астроном Галле обнаружил Нептун в указанно" Леверье месте.
2 Расчет траектории планеты Нептун потребовал от Леверье нескольких месяцев кро­
потливой вычислительной работы.
15

17. Глава 1. Математическое моделирование и решение прикладных задач
знать пригодной. Конечно, необходимо дополнительное исследование в
целях установления степени достоверности модели и границ ее приме­
нимости.
На определенном этапе развития науки и техники постепенное накоп­
ление знаний приводит к моменту, когда результаты, получаемые
с помощью математической модели, вступают в противоречие с данными
практики или перестают удовлетворять ее требованиям в смысле точно­
сти. Тогда возникает необходимость модификации модели или же созда­
ния принципиально новой, более сложной модели. Таким образом, цикл
создания математической модели повторяется многократно.
Пример 1.7. Рассмотрим задачу внешней баллистики, те задачу
о движении артиллерийского снаряда. Простейшая модель (1. 1), (1.2)
дает параболическую траекторию движения снаряда, что, как было
замечено еще в XVII в , противоречит данным практики. Существен­
ным неучтенным фактором здесь является сопротивление воздуха.
Приведенная ниже модификация модели Галилея принадлежит
И. Ньютону 1• Известно, что сила лобового сопротивления воздуха F про­
порциональна квадрату скорости, т.е. F = -pv2. При этом р = 0.5СSp, где
р - плотность воздуха; S - площадь поперечного сечения; С - коэф­
фициент лобового сопротивления (для многих задач баллистики С о:: 0.15).
Обозначим через Fx и FY горизонтальную и вертикальную проек­
ции вектора лобового сопротивления. Заметим, что FxlF = ulv, F/F =
= wlv, v = Ju2 + w2 (рис. 1.2). Следовательно, Fx = -puJu2+ w2, FY =
= -pwJu2 + w2.
Пусть т - масса снаряда. Тогда в силу второго закона Ньютона
справедливы уравнения
т dи = _AuJu2 + w2
dt ~ '
(1 4)
Рис. 1.2
1 Исаак Ньютон (1643-1727) - английский физик, механик, астроном и математик,
заложивший основы современного естествознания.
16

18. § 1.2. Основные этапы решения прикладной задачи с применением компьютера
т ~~ =-mg-f3wJu2 + w2, dy = w
dt ,
которые необходимо дополнить начальными условиями
(1.5)
u(O)=v0 cosa, w(O)=v0 sшa, х(О)=О, у(О)=О. (1.6)
Полученная модель является более сложной, чем рассмотренная
ранее модель (1.1), (.2), однако она содержит ее как частный случай.
Действительно, в случае f3 = О (сопротивление воздуха отсутствует)
уравнения (1.4)-(1.6) и (1.1), (.2) эквивалентны.
Естественно, что модель ( 1.4Н1. 6) непригодна для решения задач
современной баллистики и реально используемые модели значительно
сложнее. •
Заметим, что работа по созданию математической модели, как пра­
вило, проводится объединенными усилиями специалистов, хорошо
знающих предметную область, и математиков, владеющих соответст­
вующими разделами прикладной математики и способных оценить воз­
можность решения возникающих вычислительных задач.
§ 1.2. Основные этапы решения прикладной задачи
с применением компьютера
Решение серьезной прикладной задачи с использованием компью­
тера - довольно длительный и сложный процесс. С определенной сте­
пенью условности его можно разбить на ряд последовательных этапов
Выделим следующие этапы
1) постановка проблемы;
2) выбор или построение математической модели;
3) постановка вычислительной задачи;
4) предварительный (предмашинный) анализ свойств вычислитель-
ной задачи;
5) выбор или построение численного метода;
6) алгоритмизация и программирование;
7) отладка программы;
8) счет по программе;
9) обработка и интерпретация результатов;
1О) использование результатов и коррекция математической модели.
1. Постановка проблемы. Первоначально прикладная задача бывает
сформулирована в самом обшем виде исследовать некоторое явление,
спроектировать устройство, обладающее заданными свойствами, дать
прогноз поведения некоторого объекта в определенных условиях и т.д.
На данной стадии происходит конкретизация постановки задачи, и пер-
17

19. Глава 1. Математическое моделирование и решение прикладных задач
востепенное внимание при этом уделяется выяснению цели исследова­
ния. От исследователя требуется глубокое понимание существа задачи
и умение сформулировать ее так, чтобы найденное решение было полез­
ным и в то же время могло быть получено с помощью существующих
методов и в реальные сроки. Неудачная постановка проблемы может при­
вести к тому, что длительный и дорогостоящий процесс решения задачи
завершится получением бесполезных или тривиальных результатов
(в этом случае возможно и отсутствие каких-либо результатов).
Этот очень важный и ответственный этап завершается конкретной
формулировкой проблемы на языке, принятом в данной предметной
области. Знание возможностей, которые дает применение компьютера,
может оказать существенное влияние на окончательную формули­
ровку проблемы.
2. Выбор или построение математической модели. Для после­
дующего анализа исследуемого явления или объекта необходимо дать
его формализованное описание на языке математики, т.е. построить
математическую модель (см. § 1.1 ). Часто имеется возможность выбора
модели среди известных и принятых для описания соответствующих
процессов, но нередко требуется и существенная модификация извест­
ной модели, а иногда возникает необходимость в построении принци­
пиально новой модели.
Рассматриваемый этап - едва ли не самый важный и трудный. Часто
удачный выбор математической модели является решающим шагом
к достижению цели. Одна из существенных трудностей такого выбора
состоит в объективном противоречии между желанием сделать описание
явления как можно более полным (что приводит к усложнению модели) и
необходимостью иметь достаточно простую модель (чтобы была возмож­
ность реализовать ее на компьютере). Важно, чтобы сложность математи­
ческой модели соответствовала сложности поставленной проблемы. Если
поставленных целей можно достигнуть, использовав более простую
математическую модель, то ей и следует отдать предпочтение. Как пра­
вило, полезно иметь несколько упрощенных вариантов принимаемой
модели. Заметим, что грамотное упрощение модели - непростая задача,
однако анализ упрощенных моделей весьма полезен в течение всего
процесса решения задачи. Такие упрощенные модели часто позволяют
ответить на многие принципиальные вопросы и понять основные зако­
номерности поведения более сложной модели.
3. Постановка вычислительной задачи. На основе принятой
математической модели формулируют вычислительную задачу (или
ряд таких задач). Анализируя результаты ее решения, исследователь
предполагает получить ответы на интересующие его вопросы.
18

20. § 1.2. Основные этапы решения прикладной задачи с применением компьютера
4. Предварительный анализ свойств вычислительной задачи. На
этом этапе проводят предварительное (предмашинное) исследование
свойств вычислительной задачи. Большое внимание уделяют анализу кор­
ректности ее постановки, т.е. выяснению вопросов сушествования
и единственности решения, а также исследованию устойчивости решения
задачи к погрешностям входных данных (эти вопросы более подробно рас­
сматриваются в гл. 3). Такое исследование, как правило, относится
к компетенции профессиональных математиков. Тем не менее, решающему
задачу полезно быть в курсе современного состояния названных проблем,
уметь самостоятельно проводить простейшие исследования.
К сожалению, для многих имеющих практическую ценность задач
их строгое исследование в полной постановке провести не удается
и к решению приступают без детального анализа математических
свойств этих задач. Это нежелательная, но вынужденная мера, так как
в прикладных исследованиях существенное значение имеют конкрет­
ные (часто - весьма сжатые) сроки получения результата. На этом
этапе полезным оказывается изучение упрощенных постановок задачи.
Иногда для них удается провести исследование, позволяющее понять
основные особенности исходной вычислительной задачи. Особую цен­
ность имеют различные аналитические решения; они оказываются
полезными не только для анализа явления, но и как основа для тесто­
вых испытаний на этапе отладки программы.
S. Выбор или построение численного метода. Для решения
вычислительной задачи на компьютере требуется использование чис­
ленных методов.
Часто решение прикладной задачи сводится к последовательному
решению стандартных вычислительных задач, для которых разрабо­
таны эффективные численные методы. В этой ситуации происходит
либо выбор среди известных методов, либо их адаптация к особенно­
стям решаемой задачи. Однако если возникающая вычислительная
задача является новой, то не исключено, что для ее решения не суще­
ствует готовых методов. Построение численного метода для такой
задачи может оказаться очень трудной проблемой и потребовать при­
влечения специалиста по вычислительной математике. Умение разли­
чать отмеченные две ситуации необходимо, и наличие его уже говорит
об определенной квалификации в области вычислительных методов.
Для решения одной и той же вычислительной задачи обычно может
быть использовано несколько методов. Необходимо знать особенности
этих методов, критерии, по которым оценивается их качество, чтобы
выбрать метод, позволяющий решить проблему наиболее эффективным
образом. Здесь выбор далеко не однозначен. Он существенно зависит
19

21. Глава 1. Математическое моделирование и решение прикладных задач
от требований, предъяаляемых к решению, от имеющихся в наличии
ресурсов, от доступной для использования вычислительной техники и т.д.
Возникающим на этом этапе вопросам и посвящена большая часть
данной книги.
6. Алгоритмизация и программирование. Как правило, выбранный
на предыдущем этапе численный метод содержит только принципиаль­
ную схему решения задачи, не включающую многие детали, без которых
невозможна реализация метода на компьютере. Необходима подробная
детализация всех этапов вычислений, для того чтобы получить реализуе­
мый на компьютере алгоритм. Состааление программы сводится к пере­
воду этого алгоритма на выбранный язык программирования. Заметим,
что в настоящее время для вычислительных задач наиболее широко
используются алгоритмические языки СИ++ и ФОРТРАН.
В книге значительное место уделяется алгоритмам (в гл. 3 обсужда­
ются их общие свойства и критерии оценки качества) и практически не
рассматриваются вопросы собственно программирования. Конечно, алго­
ритмизация и программирование очень тесно связаны. Более того, прак­
тика показывает, что небольшие, на первый взгляд, различия в програм­
мах могут привести к значительным различиям в их эффективности. Тем
не менее, вопрос разработки качественного программного продукта мы
не затрагиваем (этому предмету посвящено большое число пособий).
Подчеркнем лишь, что большинство пользователей справедливо предпо­
читает строить свои программы из готовых модулей и использовать стан­
дартные программы, реализующие те или иные алгоритмы. Разумеется,
отсутствие в библиотеке стандартных программ той или иной программы
не должно быть непреодолимым препятствием.
7. Отладка программы. На этом этапе с помощью компьютера
выявляют и исправляют ошибки в программе.
Как правило, начинающий пользователь компьютера убежден, что
ошибок в составленной им программе нет или же они могут быть легко
обнаружены и исправлены. Однако совершенно неожиданно для него
отладка программы и доведение ее до рабочего состояния нередко ока­
зывается длительным и весьма трудоемким процессом. Приобретая
определенный опыт в составлении и отладке сравнительно сложных
программ, пользователь убеждается в справедливости популярного
афоризма: «В любой программе есть по крайней мере одна ошибка».
Таким образом, наличие в программах ошибок - вполне нормаль­
ное и закономерное явление, поэтому подготовку к отладке следует
начинать уже на этапе алгоритмизации и программирования. Заметим,
что эффективность отладки самым существенным образом зависит от
общей методики разработки программ.
20

22. § 1.2. Основные этапы решения прикладной задачи с применением компьютера
После устранения ошибок программирования необходимо про­
вести тщательное тестирование программы - проверку правильности
ее работы на специально отобранных тестовых задачах, имеющих
известные решения.
8. Счет по программе. На этом этапе происходит решение задачи
на компьютере по составленной программе в автоматическом режиме.
Этот процесс, в ходе которого входные данные с помощью компью­
тера преобразуются в результат, называют вычислительным процес­
сом. Как правило, счет повторяется многократно с различными вход­
ными данными для получения достаточно полной картины
зависимости от них решения задачи.
Первые полученные результаты тщательно анализируются, для
того чтобы убедиться в правильности работы программы и пригодно­
сти выбранного метода решения. Счет по программе продолжается
несколько секунд, минут или часов. Именно быстротечность этого
этапа порождает распространенную иллюзию о возможности решать
важные прикладные задачи на компьютере в очень короткое время. В
действительности же, конечно, необходимо принимать во внимание
весь цикл от постановки проблемы до использования результатов. Для
серье1ных задач часто полезные результаты получаются только в
результате многолетней работы.
9. Обработка и интерпретация результатов. Полученные в
результате расчетов на компьютере выходные данные, как правило,
представляют собой большие массивы чисел. Начинающий пользователь
часто пытается вывести эти массивы на печать, чтобы «потом провести
их анализ». Обычно первый же опыт анализа распечатки, содержащий
сотни тысяч чисел, приводит к пониманию того, что эта работа непо­
сильна для человека и следует постараться возложить ее на компьютер.
Часто первоочередной интерес представляет лишь небольшая часть
полученной информации (например, значения одной из функций в
выделенных точках) или даже некоторая грубая интегральная характе­
ристика (максимальное или минимальное значение, оценка энергии
системы и т.д.).
Для того чтобы исследователь мог воспользоваться результатами
расчетов, их необходимо представить в виде компактных таблиц, гра­
фиков или в иной удобной для восприятия форме. При этом следует,
максимально использовать возможности компьютера для подготовки
такой информации и ее представления с помощью печатающих и гра­
фических выходных устройств.
Для правильной интерпретации результатов расчетов и оценки их
достоверности от исследователя требуется глубокое знание существа
21

23. Глава 1. Математическое моделирование и решение прикладных задач
решаемой инженерной задачи, ясное представление об используемой
математической модели и понимание (хотя бы в общих чертах) особен­
ностей применяемого вычислительного метода.
Вопросы обработки и интерпретации результатов вычислений будут
затронуты при рассмотрении конкретных вычислительных методов
и алгоритмов.
10. Использование результатов и коррекция математической
модели. Завершающий этап состоит в использовании результатов расче­
тов в практической деятельности, иначе говоря, во внедрении результа­
тов. Не стоит огорчаться, если большинство полученных сначала резуль­
татов окажется бесполезным. Действительно полезные для практики
результаты являются плодом серьезной целенаправленной работы,
в процессе которой цикл решения задачи повторяется неоднократно.
Очень часто анализ результатов, проведенной на этапе их обработки
и интерпретации, указывает на несовершенство используемой матема­
тический модели и необходимость ее коррекции. В таком случае мате­
матическую модель модифицируют (при этом она, как правило, услож­
няется) и начинают новый цикл решения задачи.
§ 1.3. Вычисnитеnьный эксперимент
Создание математических моделей и решение прикладных задач
с применением компьютера требует выполнения большого объема
работ (см. § 1.1, 1.2). Нетрудно заметить аналогию с соответствую­
щими работами, проводимыми при организации натурных эксперимен­
тов: составление программы экспериментов, создание эксперименталь­
ной установки, выполнение контрольных экспериментов, проведение
серийных опытов, обработка экспериментальных данных и их интер­
претация и т.д. Однако вычислительный эксперимент проводится не
над реальным объектом, а над его математической моделью, и роль экс­
периментальной установки играет компьютер, оснащенный специально
разработанным пакетом прикладных программ. В связи с этим естест­
венно рассматривать проведение больших комплексных расчетов при
решении прикладных и научных задач как вычислительный экспери­
мент, а описанную в предыдущем параграфе последовательность эта­
пов решения как один его цикл.
Широкое применение компьютеров в математическом моделирова­
нии, разработанная теория и значительные практические результаты
позволяют говорить о вычислительном эксперименте как о новой тех­
нологии и методологии научных и прикладных исследований. Серьезное
внедрение вычислительного эксперимента в прикладные исследования
22

24. § 1.3. Вычислительный эксперимент
лишь начинается, но там, где оно происходит реально (в авиационной
и космической промышленности), его плоды весьма весомы.
Отметим некоторые достоинства вычислительного эксперимента по
сравнению с натурным. Вычислительный эксперимент, как правило,
дешевле физического. В этот эксперимент можно легко и безопасно
вмешиваться. Его можно повторить еще раз (если в этом есть необходи­
мость) и прервать в любой момент. В ходе этого эксперимента можно
смоделировать условия, которые нельзя создать в лаборатории.
Заметим, что в ряде случаев проведение натурного эксперимента
затруднено (а иногда и невозможно), так как изучаются быстропроте­
кающие процессы, исследуются труднодоступные или вообще пока
недоступные объекты. Часто проведение полномасштабного натурного
эксперимента сопряжено с губительными или непредсказуемыми
последствиями (ядерная война, поворот сибирских рек) или с опасно­
стью для жизни или здоровья людей. Нередко требуется исследование
и прогнозирование результатов катастрофических явлений (авария
ядерного реактора АЭС, глобальное потепление климата, землетрясе­
ние). В этих случаях вычислительный эксперимент может стать основ­
ным средством исследования. Заметим, что с его помощью оказывается
возможным прогнозировать свойства новых, еще не созданных конст­
рукций и материалов на стадии их проектирования.
Существенным недостатком вычислительного эксперимента явля­
ется то, что применимость его результатов ограничена рамками приня­
той математической модели.
Конечно, вычислительный эксперимент никогда не сможет полно­
стью заменить натурный, и будущее за их разумным сочетанием. Дей­
ствительно, построение математической модели основано на результа­
тах наблюдений, опыта, а достоверность ее выводов проверяется с
помощью критерия - практики.
Для прикладных задач характерно наличие значительного числа пара­
метров (конструктивных, технологических и др.). Создание нового изде­
лия или технологического процесса предполагает выбор среди большого
числа альтернативных вариантов, а также оптимизацию по ряду парамет­
ров. Поэтому в ходе вычислительного эксперимента расчеты проводятся
многократно с разными значениями входных параметров. Для получения
нужных результатов с требуемой точностью и в приемлемые сроки необ­
ходимо, чтобы на расчет каждого варианта тратилось минимальноr
время. Именно поэтому при создании программного обеспечения так
важно использовать эффективные численные методы.
Разработка программного обеспечения вычислительного экспери­
мента в конкретной области прикладной деятельности приводит к созда­
нию крупного программного комплекса. Он состоит из связанных между
23

25. Глава 1. Математическое моделирование и решение прикладных задач
собой прикладных программ и системных средств, включающих сред­
ства, предоставляемые пользователю для управления ходом вычисли­
тельного эксперимента, обработки и представления его результатов.
Такой комплекс программ иногда называют пробле.мно-ориентирован­
ным пакетом прикладных програм,~1.
§ 1.4. Допоnнитеnьные замечани1
1. Математическое моделирование является основой современной
методологии решения прикладных задач, и его роль объективно возрас­
тает в связи с необходимостью решения все более сложных приклад­
ных проблем.
2. Эффективность применения компьютера в той или иной области
науки и техники тем выше, чем совершеннее ее математические
модели. В то же время использование компьютера для исследования
каких-либо процессов часто служит серьезным стимулом для создания
новых математических моделей и детального изучения лих процессов
другими методами.
3. Само по себе применение компьютера не позволяет решить
прикладную задачу, а лишь дает в руки исследователя мощный инст­
румент познания. Использование компьютера не только не освобож­
дает от необходимости глубоко осмыслить решаемую проблему, но и
заставляет уделять постановке задачи гораздо больше внимания.
4. Вычислительный эксперимент не противоречит натурному экс­
перименту и классическому математическому анализу прикладной
задачи, а, напротив, находится с ними в органическом единстве.
5. Для успешного применения метода математического моделирова­
ния с использованием компьютера необходимо гармоническое владе­
ние всеми его составляющими. В настоящем пособии основное внима­
ние уделено вычислительным методам и алгоритмам, анализу свойств
вычислительных задач, интерпретации получаемых результатов.
6. Дополнительную информацию о методологии современного м~rrема­
тическоrо моделирования и концепции вычислительного эксперимента
можно получить из следующих источников: [58, 71, 79, 96, 99, 11 *].
7. В настоящее время большое количество высококачественных про­
грамм и пакетов программ распространяется бесплатно. Например,
через lnternet по адресу http://www.netlib.org доступно программное
обеспечение, предназначенное для решения широкого спектра приклад­
ных задач. Кроме того, по адресу http://www.acm.org/pubs/cago можно
найти 866 тщательно разработанных программ, реализующих эффек­
тивные вычислительные алгоритмы.
24

26. Глава 2
ВВЕДЕНИЕ В ЭЛЕМЕНТАРНУЮ ТЕОРИЮ
ПОГРЕШНОСТЕЙ
§ 2. 1. Источники и классификация погреwностей
результата численного реwения задачи
Для правильного понимания подходов и критериев, используемых
при решении прикладной задачи с применением компьютера, очень
важно с самого начала признать, что получить точное значение реше­
ния практически невозможно и не в этом цель вычислений. Получае­
мое на компьютере решение у• почти всегда (за исключением некото­
рых весьма специальных случаев) содержит погрешность, т.е. является
приближенным. Невозможность получения точного решения следует
уже из ограниченной разрядности компьютера.
Наличие погрешности решения обусловлено рядом весьма глубоких
причин. Перечислим их.
1. Математическая модель является лишь приближенным описа­
нием реального процесса. Характеристики процесса, вычисленные в
рамках принятой модели, заведомо отличаются от истинных характери­
стик, причем их погрешность зависит от степени адекватности модели
реальному процессу.
2. Исходные данные, как правило, содержат погрешности,
поскольку они либо получаются в результате экспериментов (измерений),
либо являются результатом решения некоторых вспомогательных задач.
3. Применяемые для решения задачи методы в большинстве слу­
чаев являются приближенными. Найти решение возникающей на прак­
тике задачи в виде конечной формулы возможно только в отдельных,
очень упрощенных ситуациях.
4. При вводе исходных данных в компьютер, выполнении арифме­
тических операций и выводе результатов на печать производятся округ­
ления.
Пусть у - точное значение величины, вычисление которой является
целью поставленной задачи. Соответствующая первым двум из указан­
ных причин погрешность «'>ну называется неустранимой погрешно­
стью. Такое название вызвано тем, что принятие математической модели
и задание исходных данных вносит в решение погрешность, которая
25

27. Глава 2. Введение в элементарную теорию поrрешностей
не может быть устранена далее. Единственный способ уменьшить эту
погрешность - перейти к более точной математической модели и
задать более точные исходные данные.
Погрешность Бму, источником которой является метод решения
задачи, называется погрешностью метода, а погрешность Ь8 у, возни­
кающая из-за округлений при вводе, выводе и вычислениях, - вычис­
лительной погрешностью. Таким образом, полная погрешность резуль­
тата решения задачи на компьютере Бу = у - у• складывается из трех
составляющих: неустранимой погрешности, погрешности метода и
вычислительной погрешности, т.е. Бу = Бну + Бму + Ь8 у.
Будем далее исходить из предположения, что математическая модель
фиксирована и входные данные задаются извне, так что повлиять на зна­
чение величины Бну в процессе решения задачи действительно нельзя.
Однако это совсем не означает, что предварительные оценки значения
неустранимой погрешности не нужны. Достоверная информация о
порядке величины Б"у позволяет осознанно выбрать метод решения
задачи и разумно задать его точность. Желательно, чтобы погрешность
метода была в 2-10 раз меньше неустранимой погрешности. Большее
значение Б"у ощутимо снижает точность результата, меньшее - обычно
требует увеличения затрат на вычисления, практически уже не влияя на
значение полной погрешности. Иногда характер использования резуль­
тата таков, что вполне допустимо, чтобы погрешность Бму была срав­
нима с Бну или даже несколько превышала ее.
Значение вычислительной погрешности (при фиксированных
модели, входных данных и методе решения) в основном определяется
характеристиками используемого компьютера. Желательно, чтобы
погрешность Ь8у была хотя бы на порядок меньше погрешности метода
и совсем не желательна ситуация, когда она существенно ее превышает.
Умение анализировать погрешности при решении прикладной
задачи и соблюдать между ними разумный компромисс позволяет
существенно экономить используемые ресурсы и является признаком
высокой квалификации.
§ 2.2. Приближенные числа.
Абсолютная и относительная погрешности
В § 2.1 было отмечено, что числа, получаемые при решении на ком­
пьютере прикладных задач, как правило, являются приближенными.
Следовательно, вопрос о точнос.ти результатов, т.е. о мере их уклоне­
ния от истинных значений, в теории и практике методов вычислений
26

28. § 2.2. Приближенные числа. Абсолютная и относительная погрешности
приобретает особое значение. Начнем его рассмотрение с введения
основных понятий элементарной теории погрешностей.
Условимся относительно обозначений, которые в дальнейшем будут
использоваться при сравнении величин. Кроме привычных знаков «=»,
«*>>, <«», «~», будем использовать знаки приближенного равенства «==>>
и приближенного неравенства «$>>. Когда положительные величины а
и Ь являются величинами одного порядка (т.е. 10-1 $ а/Ь $ 10), будем
использовать обозначение а - Ь. Если же а много меньше Ь, то будем
писать а « Ь, что эквивалентно соотношению а/Ь « 1.
1. Абсолютная и относительная погрешности. Пусть а - точное
(вообще говоря, неизвестное) значение некоторой величины, а• -
известное приближенное значение той же величины (приближенное
число). Ошибкой или погрешностью приближенного числа а• называют
разность а-а• между точным и приближенным значениями.
Простейшей количественной мерой погрешности является абсолют­
ная погрешность
Л(а*) = la - a*I. (2.1)
Однако по значению абсолютной погрешности далеко не всегда
можно сделать правильное заключение о качестве приближения. Дейст­
вительно, если Л(а*) = 0.1, то следует ли считать погрешность большой
или нужно признать ее малой? Ответ существенным образом зависит от
принятых единиц измерения и масштабов величин. Если а == 0.3 то ско­
рее всего точность приближения невелика; если же а :::: 3 · 1О 8, то сле­
дует признать точность очень высокой. Таким образом, естественно
соотнести погрешность величины и ее значение, для чего вводится
понятие относительной погрешности (при а* О)
"'( *)Ja-a*I =Л(а*) (2_2)
u а lal lal ·
Использование относительных погрешностей удобно, в частности,
тем, что они не зависят от масштабов величин и единиц измерения.
Заметим, что для приведенного выше примера о(а*) :::: 0.33 = 33 %
в первом случае и о(а*):::: 0.33. 10-9 = 0.33. 10-7 % во втором.
Так как значение а неизвестно, то непосредственное вычисление
величин Л(а*) и о(а*) по формулам (2.1 ), (2.2) невозможно Более
реальная и часто поддающаяся решению задача состоит в получении
оценок погрешности вида
la - а• 1 ~ Л(а*),
la-a*I<;;-( *)
ial _u а '
(2.3)
(2.4)
27

29. Глава 2. Введение в элементарную теорию погрешностей
где Л(а•) и б(а•) - величины, которые мы будем называть верхними
границами (или просто границами) абсолютной и относительной
погрешностей.
Если величина Л(а•) известна то неравенство (2.4) будет выпол­
нено, если положить
i:"( *) = Л(а•)
u а а . (2.5)
Точно так же если величина б(а•) известна, то следует положить
Л(а•) = 1al8(a•). (2.6)
Поскольку значение а неизвестно, при практическом применении
формулы (2.5), (2.6) заменяют приближенными равенствами
8(а*)"" ~~а·?, Л(а*)"" la•l8(a0
). (2.7)
Замечание. В литературе по методам вычислений широко
используется термин «точность». Принято говорить о точности
входных данных и решения, о повышении и снижении точности
вычислений и т.д. Мы также будем использовать эту терминологию,
за которой скрывается довольно простой смысл. Точность в качест­
венных рассуждениях обычно выступает как противоположность
погрешности, хотя для количественного их измерения использу­
ются одни и те же характеристики (например, абсолютная и относи­
тельная погрешности). Точное значение величины - это значение, не
содержащее погрешности. Повышение точности воспринимается
как уменьшение погрешности, а снижение точности - как увеличе­
ние погрешности. Часто используемая фраза ((Требуется найти
решение с заданной точностью Е» означает, что ставится задача о
нахождении приближенного решения, принятая мера погрешности
которого не превышает заданного значения Е. Вообще говоря, сле­
довало бы говорить об абсолютной точности и относительной точ­
ности, но часто этого не делают, считая, что из контекста ясно, как
измеряется погрешность.
2. Правила записи приближенных чисел. Пусть приближенное
число а" задано в виде конечной десятичной дроби:
а•= a11an- I ". ао · 131132 ".13m.
Значащи.wи цифрами числа а• называют все цифры в его записи,
начиная с первой ненулевой слева.
28

30. § 2.2. Приближенные числа. Абсолютная и относительная погрешности
Пример 2.1. У чисел а·= О.ОШ. и а·= 0.0103000 значащие цифры
подчеркнуты. Первое число имеет три, а второе - шесть значащих
цифр. .._
Значащую цифру числа а• называют верной, если абсолютная
погрешность числа не превосходит единицы разряда, соответствую­
щего этой цифре.
Пример 2.2. Если Л(а•) = 2· I0-6 , то число а•= 0.0103000 имеет
четыре верные значащие цифры (они подчеркнуты). .._
Следует отметить, что широко распространенной ошибкой при
записи приближенных чисел является отбрасывание последних знача­
щих нулей (даже если они представляют собой верные цифры).
Замечание. Верная цифра приближенного числа, вообще
говоря, не обязана совпадать с соответствующей цифрой в записи
точного числа. Таким образом, термин «верная цифрю> не следует
понимать буквально (см. пример 2.3).
Пример 2.3. Пусть а= 1.00000, а•= 0.99999. ТогдаЛ(а*) = 0.00001
и у числа а• все подчеркнутые цифры - верные, хотя они и не совпа­
дают с соответствующими цифрами числа а. .._
Количество верных значащих цифр числа тесно связано со значением
его относительной погрешности. Приведенные ниже утверждения позво­
ляют в дальнейшем связывать точность числа с количеством его верных
значащих цифр и трактовать потерю точности как потерю верных цифр.
Предложение 2.1. 1°. Если число а• содержит N верных знача­
щих цифр, то справедливо неравенство
Б(а•) $ (ION- 1 _ 1)-1"" 10-N+ 1.
2°. Дqя того чтобы число а• содержало N верных значащих цифр,
достаточно чтобы было выполнено неравенство
Б(а•) $ (ION + 1)-1"" 10-N.
3°. Если число а• имеет ровно N верных значащих цифр, то
10-N-I ;SБ(a•);S 10-N+I
и, таким образом, Б(а*) - 10-N. •
Пр им ер 2.4. Что можно сказать об относительной погрешности
числа а·, если известно, что оно содержит три верные значащие цифры?
В силу утверждения 1° имеем Б (а*) ;S 1о-2 = 1%. .._
29

31. Глава 2. Введение в элементарную теорию nоrрешностей
Пр им ер 2.5. С какой относительной точностью следует найти
число а*, чтобы верными оказались шесть его значащих цифр?
Из утверждения 2° следует, что достаточно найти а• с относитель­
ной точностью 6::::: 10-6• .&
Заметим, что границы абсолютной и относительной погрешностей
принято записывать с одной или двумя значащими цифрами. Большая
точность в записи этих величин, как правило, не имеет смысла, так как
обычно они являются довольно грубыми оценками истинных значений
погрешностей, и кроме того, для практического использования часто
бывает достаточно знать только их порядок.
Пр им ер 2.6. Информация о погрешности вида о(а*) ::::: 0.288754 • 1o-s
практически равноценна информации о(а*) ::::: 3. 10-6' причем послед­
няя вызывает больше доверия. Скорее всего, вполне удовлетворитель­
ной в данном случае является и запись о(а*) - 10-6. .&
Неравенство (2.3) эквивалентно двойному неравенству
а• - Л(а*) $а$ а• + Л(а*)
и поэтому тот факт, что число а• является приближенным значением
числа а с верхней границей абсолютной погрешности Л(а*) [с абсо­
лютной точностью i; = Л(а*) ], принято записывать в виде
а= а* ± Л(а*).
Как правило, числа а• и Л(а*) указывают с одинаковым числом
цифр после десятичной точки.
Пр им ер 2.7. Пусть для числа а известны приближенное значение
а•= 1.648 и граница абсолютной погрешности Л(а*) = 0.002832. Тогда
можно записать а= 1.648 ± 0.003. Записи вида а= 1.648 ± 0.002832 или
а = 1.648 ± 0.1 являются неестественными. .&
Из неравенства (2.4) следует, что значение а заключено примерно
между а*(! - 8(а*)) и a*(I + 8(а*)). Поэтому тот факт, что число а•
является приближенным значением числа а с границей относительной
погрешности 8(а*) (с относительной точностью i; = 8(а*) ), принято
записывать в виде а= а• (1 ± 8(а*) ).
Пр им ер 2.8. Оценим точность часто используемого в простейших
расчетах приближения тт* = 3 14 к числу тt. Поскольку тt = 3.14159"" то
7t - тт* = 0.00159... Следовательно, можно принять Л(тт*) = 0.0016
и 8(тт*)::::: 0.0016/3 14::::: 0.00051=0.051 %. Итак, тt = 3.14(1±О051 %). .&
30

32. § 2.2. Приближенные числа. Абсолютная и относительная погрешности
Замечание. Если число а• приводится в качестве результата
без указания значения погрешности, то принято считать, что все
его значащие цифры являются верными. Начинающий пользова­
тель часто слишком доверяет выводимым из компьютера цифрам,
предполагая, что вычислительная машина придерживается того
же соглашения. Однако это совсем не так: число может быть выве­
дено с таким количеством значащих цифр, сколько потребует про­
граммист заданием соответствующего формата. Как правило,
среди этих цифр только небольшое число первых окажутся вер­
ными, а возможно верных цифр нет совсем. Анализировать резуль­
таты вычислений и определять степень их достоверности совсем
непросто. Одна из целей изучения вычислительных методов и
состоит в достижении понимания того, что можно и чего нельзя
ожидать от результатов, полученных на компьютере.
3. Округление. Часто возникает необходимость в округлении числа
а, т.е. в замене его другим числом а• с меньшим числом значащих
цифр. Возникающая при такой замене погрешность называется погреш­
ностью округления.
Существует несколько способов округления числа до п значащих
цифр. Наиболее простой из них - усечение состоит в отбрасывании
всех цифр, расположенных справа от п-й значащей цифры. Более пред­
почтительным является округление по дополнению. В простейшем вари­
анте это правило округления состоит в следующем. Если первая слева
из отбрасываемых цифр меньше 5, то сохраняемые цифры остаются без
изменения. Если же она больше либо равна 5, то в младший сохраняе­
мый разряд добавляется единица.
Абсолютное значение погрешности округления при округлении по
дополнению не превышает половины единицы разряда, соответствую­
щего последней оставляемой цифре, а при округлении усечением -
единицы того же разряда.
Пр и мер 2.9. При округлении числа а = 1.72631 усечением до трех
значащих цифр получится число а•= 1.72, а при округлении по дополне­
нию - число а•= 1.73. .6.
Границы абсолютной и относительной погрешностей принято все­
гда округлять в сторону увеличения.
Пример 2.10. Округление значений Л(а*) = 0.003721 и Б(а*)
= 0.0005427 до двух значащих цифр дает значения Л(а*) = 0.0038
и Б(а*) = 0.00055. •
31

33. Глава 2. Введение в элементарную теорию погрешностей
§ 2.3. Погрешность арифметических операций над
приближенными числами
Исследуем влияние погрешностей исходных данных на погреш­
ность результатов арифметических операций. Пусть а· и ь• - прибли­
женные значения чисел а и Ь. Какова соответствующая им величина
неустранимой погрешности результата?
Пред ложе и и е 2.2. Абсолютная погрешность алгебраической
суммы (суммы или разности) не превосходит суммы абсолютных
погрешностей стюгаемых, те.
Л(а* ± Ь*) ::; Л(а*} + Л(Ь*).
Доказательство. Имеем
Л(а* ± Ь*) = l(a ± Ь)- (а*± b*)I = (а - а•)± (Ь - b*)I ::;
::; Л(а*) + Л(Ь•). 8
Следствие. В силу неравенства (2.8) естественно положить
Л (а* ± Ь*) = Л (а*} + Л (Ь*).
(2.8)
(2.9)
Оценим относительную погрешность алгебраической суммы.
Предложение 2.3. Пусть а и Ь - ненулевые числа одного знака.
Тогда справедливы неравенства
о(а* + Ь*) ::; omax• о(а* - Ь*) ::; vomax• (2. IO)
где omax = max{o(a*), о(Ь°)}, v = la + bl!a - bl.
Доказательство. Используя формулу (2.2) и неравенство (2.8),
имеем
1а± Ь lo(a* ± Ь*) = Л(а* ± Ь*)::; Л(а") + Л(Ь*) =
= ао(а*) + IЪо(Ь*)::; (al+lbl)Omax =а+ bomax·
Из полученного неравенства сразу следуют оценки (2.1 О). 8
Следствие. В силу неравенств (2.10) естественно положить
8(а* + ь·) =8m", 8(а• - Ь*) =v8max,
где 8max = max {8 (а*), 8(Ь•)} , v = 1а + Ь 111 а - Ь 1.
(2.11)
Первое из равенств (2.11) означает, что при суммировании чисел
одного знака не происходит потери точности, если оценивать точность
в относительных единицах. Совсем иначе обстоит дело при вычитании
32

34. § 2.3. Погрешность арифметических операций над приближенными числами
чисел одного знака. Здесь граница относительной погрешности возрас­
тает в v > 1 раз и возможна сушественная потеря точности. Если числа
а и Ь близки настолько, что 1а + Ь 1 » 1а - Ь i, то v » 1 и не исключена
полная или почти полная потеря точности. Когда это происходит, гово­
рят о том, что произошла катастрофическая потеря точности.
Пр им ер 2.11. Пусть решается прикладная задача, в которой окон­
чательный результат у вычисляется по формуле у = 1 - х с помощью
предварительно определяемого значения х. Предположим, что найден­
ное приближение х• = 0.999997 к значению х содержит шесть верных
значащих цифр. Тогда у• = 1 - 0.999997 = 0.000003 и в процессе вычис­
ления оказались потерянными пять верных цифр. Если же учесть, что
б(х•) - 0.0001 %, а б(у•) - 33 %, то следует признать, что произошла
катастрофическая потеря точности.
Подчеркнем, что здесь виновником «катастрофы)) является не опера­
ция вычитания, а предложенный метод решения задачи, где оконча­
тельный результат получается с помощью вычитания двух близких
чисел. Выполнение этой операции лишь делает очевидным то, что дей­
ствительно полезная информация о значении у уже оказалась потерян­
ной до вычитания. Если нет другого варианта расчета, то для получе­
ния приемлемого результата следовало бы предварительно вычислить х
с существенно большим числом верных знаков, учитывая, что пять
старших значащих цифр при вычитании будут потеряны. .А.
Итак, получаем следующий важный вывод. При построении числен­
ного метода решения задачи следует избегать вычитания близких чисел
одного знака. Если же такое вычитание неизбежно, то следует вычис­
лять аргументы с повышенной точностью, учитывая ее потерю при­
мерно в v = la + Ь1а - Ь раз.
Предложение 2.4.Для относительных погрешностей произведе­
ния и частного приближенных чисел верны оценки
б(а* Ь°) $ б(а•)+б(Ь•)+ б(а.)б(Ь•),
8(а•1ь•) $ с(а*)+Б(ь•)
-Б(Ь•) '
в последней из которых считается, что б(Ь*) < 1.
Доказательство. Выполним следующие преобразования;
lаЬjб(а·ь·)=Л(а•ь·)= lаь-а•ь•1 =
1(а - а*)Ь + (Ь - ь·)а - (а - а·)(Ь - ь•) 1 $
(2.12)
(2.13)
$ 1ЬjЛ(а•) + 1а1 Л(Ь•) + Л(а°)Л(Ь°) = 1аЬ1 (8(а*) + б(Ь°) + 8(а*)8(Ь.)).
33

35. Глава 2. Введение в элементарную теорию погрешностей
Разделив обе части полученного неравенства на 1аЬ1. выведем
оценку (2.12).
Для вывода второй оценки предварительно заметим, что
1ь·1=1ь + (Ь. - b)I ~ 1ь1 -Л(Ь.) = lbl(l - о(Ь•)).
Тогда
о(а·1ь·)= lа!ь-а·1ь·1 = lаь·-ьа·1 =
la!bl laь*I
= 1а(Ь* - Ь) + Ь(а - a*)I < 1аlЛ(Ь°) + /ЬIЛ(а*) = S(b*) + S{a*) 8
1аь*I - 1abl(1 -о(ь*)) 1- s(ь*) .
Следствие. Если 8(а*) « 1 и Б(Ь•) « 1, то для оценки границ
относительных погрешностей можно использовать следующие при­
ближенные равенства:
8(а* ь•) ~ 8(а•)+ 8(Ь*), 8(а* !Ь*) ~ 8(а*)+ 8(Ь*). (2.14)
Именно равенства (2.14) чаще всего и используют для практической
оценки погрешности.
Итак, выполнение арифметических операций над приближенными
числами, как правило, сопровождается потерей точности. Единствен­
ная операция, при которой потеря не происходит, - это сложение
чисел одного знака. Наибольшая потеря точности может произойти при
вычитании близких чисел одного знака.
§ 2.4. Погрешность функции
1. Погрешность функции многих переменных. Пусть f(x) =
= f(x 1, х2, •.. , хт) - дифференцируемая в области G функция т перемен­
ных, вычисление которой производится при приближенно заданных зна­
чениях аргументов х~, х;, "., х:. Такая ситуация возникает, например
всякий раз, когда на компьютере производится расчет по формуле. Важно
знать, каково значение неустранимой погрешности, вызванной тем, что
вместо значения у = f(x) в действительности вычисляется значение
у•= f(x•), где х• = (х~, х;, "., х: ).
Введем обозначения: пусть [х, х*] - отрезок1, соединяющий точки
х их*, и r;. = дf/дхj.
J
1 Отрезком, соединяющим точки х их' в m-мерном пространстве, называется множе­
ство точек видаах + ( - а)х', О :5 а :5 .
34

36. § 2.4. Погрешность функции
Предложение 2.5. Для абсолютной погрешности значения
у• = f(x*) справедлива следующая оценка:
т
Л(у0 ) ~ L . max • 11;}х)1 Л(х;).
j=I х Е [х,х ]
(2.15)
До к аз ат ель ст в о. Оценка (2.15) вытекает из формулы конечных
приращений Лагранжа1:
т
f(x)-f(x0
) = L1; (х)(хгхj), хе [х,х0 ]. •
j=I j
Следствие. Если х• ""х, то в силу оценки (2.15) можно положить
- т -
Л(у0
)"" L 11;.(х0 ) 1Л(х/)'
j=I 1
(2.16)
- т
Л(у0 )"" L ll;}x) 1Л(х/). (2.17)
j=I
Равенство (2.16) удобно для практических оценок, а равенством
(2.17) мы воспользуемся в дальнейшем для теоретических построений.
Из (2.16), (2.17) вытекают приближенные равенства для оценки гра­
ниц относительных погрешностей:
- т -
о(у*)"" 2: vjo<x/),
j=I
lxjl IJ;.(x*)/
v• = J
j lt(x0
)I '
- т -
о(у*)"" 2: vjo<xj).
j=I
(2.18)
(2.19)
Пр им ер 2.12. Пусть корни квадратного уравнения х2 + Ьх + с = О
вычисляются при значениях коэффициентов Ь "" 103, с "" 1. Каково влия­
ние погрешностей задания коэффициентов на точность вычисляемых
значений?
Воспользуемся явными формулами для корней:
х1 = f(b, с)= (-Ь- ./d)l2, х2 =g(b, с)= (-Ь + ./d)!2,
где d = Ь2 - 4с.
1 Жозеф Луи Лагранж (1736--1813) - французский математик, механик и астроном.
Одии из создателей математического анализа, вариационного исчисления, классической
аналитической механики.
35

37. Глава 2. Введение в элементарную теорию nоrрешностей
Заметим, что х1 • х2 = с. Тогда при заданных значениях коэффициен­
тов получим:
Jd,,,, Jю6 -4 ::::: 103, х 1 ::::: (-03 - J03)/2 = -J03,
х2 = с/х 1 ::::: 1/(-103) = -J0-3.
Далее, имеем:
f'ь = (-1 - Ы/d)12::::: (-1 - 103/103)/2 = -1, /~ = 11/d::::: 10-3,
g'ь = (-1 + Ы/ёJ)12 = (Ь- /d)l(2/d) = -х2! Jd::::: 10-6,
g~ = -11 Jd ::::: -J0-3.
Применяя первую из формул (2.19), для корня х 1 находим:
v~ 1 = lb*l IJi,l!lx~I ::::: 1, v~. 2 = lc*l l/~l!lx~I ::::: 10-6•
Аналогично для корня х2 имеем:
v;, 1 = lb*l lgi,l!lx;I ::::: 1, v; 2 = lc*l lg~l!lx;I ::::: 1.
Таким образом,
8(х~):::::8(Ь*)+ 10-6 8(с*), 8(х;):::::8(Ь*)+8(с*). (2.20)
Следовательно, точность первого корня практически определяется
только точностью задания коэффициента Ь, в то время как коэффициент с
может быть задан очень грубо. Для второго корня влияние погрешностей
в задании коэффициентов Ь и с практически одинаково. А.
2. Погрешность функции одной переменной. Формулы для гра­
ниц погрешностей функции /(х) одной переменной являются частным
случаем формул (2.16Н2.18) при т = 1:
Л(у*)::::: IJ'(x*)IЛ(x*), Л(у*)::::: lf'(x)JЛ(x*);
8(у*)::::: v• 8(х*), 8(у*)::::: v8(x*),
где v* = ~lx....,.·~11~/~'(x.,....·)~I v = ~lx~l~l/_'("-'x)~
IJ(x*)I , lf(x)I
(2.21)
(2.22)
3. Погрешность неявной функции. Нередко· приходится сталки­
ваться с ситуацией, когда функция у= f(x), где х = (х 1 , х2, "" хт) зада­
ется не явным образом, а как решение нелинейного уравнения F(y, х) =
= О, т.е. неявно. Если для такой неявной функции воспользоваться
известными формулами вычисления частных производных
F;(y,x)I
r; (х) =- _L__() , j = 1, 2, "" т,
J F' у,х
У у=/(х)
(2.23)
36

38. § 2.5. Особенности машинной арифметики
то исследование неустранимой погрешности неявной функции сразу же
сводится к рассмотренному выше случаю.
Пр им ер 2.13. Для проведенного в примере 2.12 исследования совсем
не обязательно было выписывать явные формулы для корней. В этом слу­
чае величины х1 = /(Ь, с) и х2 =g(b, с) можно рассматривать как неявные
функции, заданные уравнением F(x, Ь, с)= О, где F = х2 + Ьх +с.
Здесь F; = 2х + Ь, F'ь = х, F; = 1. Следовательно,
• 1ь1 IF//F;l Iv ------l,i- lxl
х=х;, Ь=1оз, c=I
103
:::::----
12х;+103
Вычисления при i = , х; ::::: -103 и i = 2, х; ::::: -10-3 дают те же зна­
чения коэффициентов v;, 1 , v;, 2 , v;, 1 , v;, 2 , что и в примере 2.12, а
следовательно, те же формулы (2.20). .А.
§ 2.5. Особенности машинной арифметики
Знание основных особенностей машинной арифметики необходимо
для грамотного использования компьютеров при решении научно-тех­
нических задач. Пользователь, не учитывающий эти особенности, вряд
ли может рассчитывать на высокую точность и эффективность вычис­
лений. Невнимание к ним часто приводит к неверным результатам.
Подчеркнем, что в основе причин появления вычислительной погреш­
ности лежит сам способ представления чисел в компьютерах.
1. Системы счисления. Принятый способ записи чисел состоит
в представлении их упорядоченным набором цифр. В привычной нам
десятичной позиционной системе счисления вещественное число х
представляют последовательностью символов, которая начинается со
знака(+ или-) и продолжается цепочкой десятичных цифр а; и pj, раз­
деленных десятичной точкой·
(2.24)
Здесь каждой позиции (разряду), которую занимает цифра относи­
тельно десятичной точки, отвечает определенная степень числа 10.
37

39. Глава 2. Введение в элементарную теорию погрешностей
По существу, равенство (2.24) представляет собой принятую форму
сокращенной записи разложения числах в сумму по степеням 10:
х = ±(ап · 1оп + ". + а1 · 101 +а0 ·10° + р1 · 10-1+
+ Р2 • 10-2 + ".+Рт• 10-т + ".).
Пример 2.14. Запись х = 20.5 означает, что х = 2·101 +О·10° +
+5·10-1.&
Для представления чисел в компьютере также используют позици­
онные системы счисления, однако основаниями систем служат, как пра­
вило, степени числа 2. Это вызвано способом хранения чисел в устрой­
ствах памяти компьютера, каждое из которых можно рассматривать как
набор однотипных элементов, способных находиться только в одном из
двух возможных устойчивых состояний - «ВКЛЮЧеЮ) или «ВЫКЛЮЧеЮ),
Эти состояния интерпретируются соответственно как О или 1 - значе­
ние двоичной цифры. Наиболее распространены системы счисления с
основанием 2 (базисная двоичная система счисления), 8 и 16.
Игнорируя некоторые малосущественные детали, будем считать, что
все вычислительные машины работают в двоичной системе счисления.
В ней вещественное число х по-прежнему записывается в виде (2.24),
однако а, и р1 -уже двоичные цифры (О или 1). В этом случае число х
разлагается в сумму по степеням числа 2:
х = ±(ап. 2п + ". + al. 21 + ао. 20 + Р1. 2-1 + Р2. 2-2 +".+Рт. 2-т + ".).
Пр им ер 2.15. Запишем число х = 20.5 в двоичной системе счисле­
ния. Для этого разложим его в сумму по степеням числа 2:
х = 1· 24 +о· 23 + 1 •22 +о· 21+о· 2° + 1 · 2-1.
Опуская степени числа 2, получаем х = (1О100.1 )2. Здесь нижний
индекс 2 указывает на основание системы счисления. А
Для хранения числа в памяти компьютера отводится поле стандарт­
ной длины (машинное слово), в котором число записывают в виде
последовательности двоичных цифр. По форме представления, способу
хранения и реализации арифметических операций сушественно разли­
чаются два типа используемых в компьютерах чисел: целые числа и
вещественные числа.
2. Представление целых чисел. Целое число п представляют в виде
(2.25)
38

40. § 2.5. Особенности машинной арифметики
где L - некоторое стандартное для компьютера целое число, а, - дво­
ичные цифры. Всего для хранения числа п отводят s = L + 2 разрядов
(один из них для хранения знака).
Из представления (2.25) видно, что максимальное по модулю целое
число, представимое в компьютере, есть п max = 2L + ... + 21 +2о= 2L + 1- l.
Обычно оно не очень велико. Например, при стандартном формате
записи целых чисел в компьютерах s = 32 и пmах = 231 - l ~ 2 • 109.
Операции сложения, вычитания и умножения над целыми числами
реализованы так, что если результат не превышает по модулю число
птах, то он получается точным. Отметим, однако, следующую неприят-
ную особенность. Если модуль результата превышает пmах• то на боль­
шинстве компьютеров эта ситуация не доводится до сведения пользо­
вателя, происходит присвоение результату некоторого значения
(меньшего пmах по модулю) и вычисления продолжаются далее.
3. Представление вещественных чисел. В современных компью­
терах для вещественных чисел принята форма представления с плаваю­
щей точкой, когда каждое число представляют в виде
Х = ±(yl • 2-1 + У2 •2-2 + ". + У1 • 2-1)2Р. (2.26)
Здесь у 1 , у2, "., у1 - двоичные цифры.
Как правило, число х нормализуется так, чтобы у1 = 1, и поэтому в
памяти компьютера хранятся только значащие цифры соответствующеm
нормализованного числа. Числоµ= ±(у 1 · 2-1+ у2 • 2-2 + ". + у1 • 2-1) назы­
вается мантиссой числа х. Количество t цифр, которое отводится для
записи мантиссы, называемое разрядностью мантиссы, зависит от кон­
структивных особенностей конкретной вычислительной машины, но
всегда является конечным. В представлении (2.26) р - целое число,
называемое двоичным порядком. Порядок также записывают как двоич­
ное целое число р = ±(а 1а1 _ 1 ". а 0) 2, для хранения котороm
в машинном слове отводится l + 2 двоичных разрядов. На рис. 2.1 схе­
матически представлена структура машинного слова для хранения
вещественного нормализованного числа.
Мантисса Двоичный порядок
Рис. 2.1
39

41. Глава 2. Введение в элементарную теорию погрешностей
Пример 2.16. Представим число х = 20.5 в виде двоичного нор­
мализованного числа. Так как х= (10100.1)2 (см. пример 2.15), то,
перемещая двоичную точку на пять позиций влево, получаем х =
= (0.101001)2· 2s. .А.
Длительное время различные компьютеры отличались друг от друга
числом разрядов, отводимых для хранения мантиссы и порядка, спосо­
бом округления и имели различные правила машинной арифметики.
Однако в настоящее время большинство компьютеров (в том числе -
все персональные компьютеры) конструируются в соответствии с раз­
работанным в 1985 году IEEE - стандартом двоичной арифметики
(IEEE Floating Point Standard). При стандартном способе записи норма­
лизованного числа х в IEEE арифметике под хранение мантиссы отво­
дится 24 разряда (включая знак), а под хранение двоичного порядка -
8 разрядов. Поскольку для нормализованноm числа всегда у1 = l, то
необходимости в хранении первого значащего разряда нет, и сэконом­
ленный разряд используется для хранения еще одного двоичного раз­
ряда мантиссы.
Поскольку у 1 = l, то для мантиссы нормализованного числа спра­
ведливы оценки 0.5 s 1µ1 < l. В то же время для представления
порядка используется конечное число / + l двоичных цифр и поэтому
-(2 1+ 1 - 2) =Pm10 s р s Ртах = 2 1+ 1 - l. Таким образом, для представи­
мых на компьютере нормализованных чисел имеем О < Х0 s lxl < Х00, где
Pm1n- 1 Ртах
Х0 = 2 , Х"' = 2 . Числа Х0 и Х00 иногда называют порогом
машинного нуля и порогом переполнения.
На компьютерах, удовлетворяющую стандарту IEEE, в арифметике
обычной точности Рmш = -126, Pmax = 127 и поэтому Х0 = 2-127 :о: l0-38,
х"' =2127,., 1038.
Кроме нормализованных чисел IEEE арифметика включает в себя
еще и субнормальные (денормализованные) числа. Субнормальные
числа - очень малые числа из диапазона (-Х0, Х0), которые возникают
в процессе вычислений и не могут быть представлены в нормализован­
ном виде. Они также представляются в виде (2.26), но с у 1 =О и мини-
мально возможным показателем р = Pm10• Напомним, что в IEEE ариф­
метике обычной точности Х0 ,., l0-38.
40

42. § 2.5. Особенности машинной арифметики
Пример 2.17. Число х = 2-130 не может быть представлено в IEEE
арифметике обычной точности как нормализованное число. Оно представ­
ляется как субнормальное число видах= (0.00010 ... 0)2 • 2-126. .&
Заметим, что нуль - особое ненормализуемое число. Оно представ­
ляется в IEEE арифметике как +О и -0. Числа +О и -О считаются рав­
ными, но в некоторых случаях они могут проявлять себя по разному. В
представлении (2.26) нуль имеет нулевую мантиссу и показатель cтe-
Pmin - 1
пени р = Pmin - 1, т.е. ±О = ±(О.ООО ... 0)2 • 2
На основании имеющихся сведений о представлении чисел в ком­
пьютере можно сделать ряд важных выводов.
1°. В компьютере представимы не все числа, а лишь конечный
набор рациональных чисел специального вида. Эти числа образуют
представимое множество компьютера. Для всех остальных чисел х
возможно лишь их приближенное представление с ошибкой, которую
принято называть ошибкой представления (или ошибкой округления).
Обычно приближенное представление числа х в компьютере обозна­
чают как х• = fl(x) 1• В IEEE арифметике округление производится по
дополнению, поэтому для нормализованных чисел граница относитель­
ной погрешности представления равна единице первого отброшенного
разряда мантиссы, т.е. S(х*) = ~;м = 2-1 (порядок числа не влияет на
относительную погрешность представления). Величина ~;м играет в
вычислениях на компьютере фундаментальную роль; ее называют
относительной точностью компьютера, а также машинной точно­
стью (или машинным эпсилон). Всюду в дальнейшем ~;м - это относи-
тельная точность компьютера. Заметим, что значение этой величины
определяется разрядностью мантиссы и способом округления.
Важно с самого начала иметь четкое представление о том, что почти
наверняка в представимом множестве компьютера нет числа у, являю­
щегося решением поставленной задачи. Лучшее, что можно попытаться
сделать, - это найти его представление у*= fl(y) с относительной точ­
ностью порядка ~;м .
Полезно отметить, что среди представимых в компьютере чисел
нет не только ни одного иррационального (в том числе и таких важ-
ных постоянных, как 7t, е, J2 ), но и даже такого широко используе­
мого в вычислениях числа, как 0.1. Дело в том, что двоичная запись
числа 0.1 является бесконечной периодической дробью: 0.1
1 fl - начальные буквы английского слова floatшg - «плавающий».
41

43. Глава 2. Введение в элементарную теорию погрешностей
= (0.0001100110011 ...)2• Поэтому это число всегда представляется в
компьютере приближенно, с погрешностью, вызванной необходимо­
стью округления.
2°. Диапазон изменения чисел в компьютере ограничен. Нормализо­
ванные числа расположены в интервалах (-Х00, -Х0) и ( Х0, Х00), где зна­
чения Х0 и Х00 определяются числом разрядов, отведенных для хранения
двоичного порядка.
3°. Все числа х, по модулю большие Х00 , рассматриваются как
машинная бесконечность и представляются в IEEE арифметике симво­
лами -<YJ или +оо. Получение числа х такого, что lxl > Х0 называют пере­
полнением. Получение числах такого, что lxl < Х0, называют исчезнове­
нием порядка или антипереполнением. Обычно при антипереполнении
генерируется субнормальное число или полагается fl(x) =О и вычисле­
ния продолжаются.
Замечание. Не следует смешивать машинную точность &м,
порог машинного нуля Х0 и минимальное представимое на компью­
тере положительное субнормальное число хтш. Это совершенно раз­
ные числа, причем xmin « Х0 « & м. В IEEE арифметике обычной
точности хmш"' 10-43, х"' 10-зs и &м"' 10-1.
4°. На машинной числовой оси (рис. 2.2) числа расположены нерав­
номерно. Плотность их возрастает по мере приближения к нулю и
падает с удалением от нуля. Чтобы убедиться в этом, заметим, что рас-
стояние от одного нормализованного числа х = µ · 2Р до другого бли­
жайшего нормализованного равно единице последнего разряда ман-
тиссы, умноженной на 2Р, т.е. равно 2Р - t. Так как t фиксированно, то
расстояние уменьшается с уменьшением значения порядка р и возрас­
тает с увеличением р. Субнормальные числа распределены на интер­
вале (-Х0, Х0) равномерно (см. рис. 2.2), расстояние между соседними
Pmin-t
субнормальными числами равно 2
-Х
r -Хо -О +О
+ lr
~~-Оrр--и-ца~те-л-ь-ны_е_~,-С_уб_н_о_рм~ал-ьн_ы_е~-П-ол-ожите~-л-ь_н_ы_е~ +оо
нормалиэованные числа нормалиэованные
числа числа
Рнс. 2.2
42

44. § 2.5. Особенности машинной арифметики
4. Арифметические операции над числами с плавающей точ­
кой. Правила выполнения арифметических операций в двоичной сис­
теме счисления чрезвычайно просты и легко реализуются на компью­
тере. Однако в силу ограниченной разрядности мантиссы операции
сложения, вычитания, умножения и деления над представимыми
в компьютере вещественными числами не могут быть реализованы
точно. Дело в том, что арифметические операции над числами, ман­
тиссы которых содержат t разрядов, приводят, как правило, к резуль­
татам, содержащим более t разрядов. Округление результата до t раз­
рядов и служит главным источником погрешности. Для того чтобы
отличать машинные арифметические операции от идеальных матема­
тических операций +, -, х, :, будем обозначать их через Е!Э, 8, ®, О.
Игнорируя несущественные детали, можно считать, что результат
машинной арифметической операции совпадает с результатом точного
выполнения той же операции с погрешностью, приближенно равной
погрешности округления. Таким образом,
Л(а Е1Э Ь)::::: la + bli:м, Л(а е Ь)::::: la - bli:",
Л(а ® Ь)::::: la х bli:", Л(а ОЬ)::::: la: bli:".
Конечно, в некоторых ситуациях округление может отсутствовать.
Например, полезно знать, что умножение и деление числа на целую
степень числа 2 выполняется на компьютере точно, так как в этом слу­
чае мантисса не меняется.
Пр им ер 2.18. Рассмотрим гипотетический компьютер, в котором
числа представляются всего лишь с шестью двоичными разрядами ман­
тиссы, а округление производится по дополнению. Пусть на таком ком­
пьютере вычисляются сумма и произведение двух представимых на ней
чисел а= 20.5 = (10100.1)2 и Ь = 1.75 = (1.11)2. Производим вычисления в
двоичной арифметике:
а+ Ь = (10100.1)2 + (1.11)2 = (10110.01)2,
ах Ь = (10100.1)2 х (1.11)2 = (100011.111)2•
После округления до шести значащих цифр получим а Е1Э Ь =
=(10110.1)2 = 22.5, а®Ь = (100100.)2 = 36. Очевидно, что эти резуль-
таты отличаются от точных значений а+ Ь = 22.25, ах Ь = 35.875. .&
Заметим, что машинные арифметические операции обладают иными
свойствами, нежели обычные математические операции. Например, не
выполняется известное правило арифметики «ОТ перемены мест слагае­
мых сумма не меняется». Покажем это на примере.
43

45. Глава 2. Введение в элементарную теорию погрешностей
Пр нм ер 2.19. Пусть вычисления производятся на компьютере из
примера 2.17. причем а = (1.)2, Ь = с= (0.000001)2. Тогда а+ Ь =
= (1.000001 )2 и после округления имеем а 0 Ь = (1.00001 )2. Далее,
(а0 Ь)+ с= (1.000011)2 и после округления получим (а 0 Ь) 0 с=
=(1.00010)2• Сложение в ином порядке дает с 0 Ь = (0.000010)2, (с 0 Ь) 0
0 а= (1.00001)2• Таким образом, (а 0 Ь) 0 с:!: (с 0 Ь) 0 а. .&
5. Двойная точность. На компьютерах, удовлетворяющих IEEE
стандарту, при вычислениях с обычной точностью, нормализованные
числа расположены в диапазоне 1о-38 ~ lxl ~ 1038, вполне достаточ­
ном для большинства приложений. Однако разрядность мантиссы t
невелика и поэтому & - 10-7; в десятичной арифметике это эквива­
лентно тому, что мантисса содержит семь десятичных цифр.
На большинстве компьютеров возможна реализация арифметиче­
ских действий над числами, разрядность мантиссы которых примерно
вдвое превосходит стандартную разрядность t. Это приводит к суще­
ственному повышению машинной точности. Например на компьютерах,
удовлетворяющую стандарту IEEE, для представления чисел двойной
точности отводится 53 разряда для хранения мантиссы (включая знак)
и 11 разрядов для хранения порядка. Здесь Х0 "' 10-3°8, Х00 "' 1озо8 и
&14 - 10-16• Для сравнения напомним, что обычная точность этих
компьютеров есть &14 - 10-7, так что следует говорить не об удвоении
точности, а о повышении точности на много порядков.
В IEEE арифметике есть еще режим расширенной двойной точ­
ности, в котором для представления мантиссы отводится 65 разрядов
(включая знак), а для представления порядка - 15 разрядов. В этом
режиме Х0 "' 10-4964, Х00 "' 104964 и&" - 10-19 . Подчеркнем, что исполь­
зование режимов двойной или расширенной двойной точности отнюдь
не позволяет ликвидировать погрешность округления, а только лишь
уменьшает ее значение.
6. Вычисление машинного &. Для приближенного вычисления
величины & м удобно воспользоваться следующим определением.
Машинное эпсилон - это минимальное из представимых на компью­
тере положительных чисел &, для которых 1 GЭ & > 1.
Величину &14 можно оценить непосредственно в ходе вычислитель­
ного процесса. Для этого достаточно включить в программу фрагмент,
реализующий следующий метод. Полагая е<0> = 1, следует вычислять
последовательно е< 1 > = О.5е<О>, e<2J = 0.5&(1>, "., е(п) = 0.5&(п - IJ, ".,
44

46. § 2.5. Особенности машинной арифметики
запоминая получающиеся значения E(n) в памяти компьютера и прове­
ряя каждый раз выполнение неравенства 1 Е0 E(n) > 1. Как только при
некотором п окажется, что 1 Е0 Е (n) = 1, следует положить Е" = Е (n - 1) и
перейти к следующему этапу вычислений. Хотя полученное таким спо­
собом значение может отличаться от Е" в два раза, обычно оно исполь­
зуется так, что эта погрещность не имеет значения.
Пример 2.20. Покажем, что Ем = 2- 6 = (0.000001)2 - машинное
эпсилон для компьютера из примера 2.18. В самом деле, 1 + Ем =
= (1.000001)2 и после округления имеем 1 Е0 Ем= (1.00001)2 > 1. Если же
к 1 добавить любое положительное Е < Ем, то в седьмом разряде резуль­
тата будет стоять нуль и после округления получим 1 Е0 Е = 1. •
Всюду в дальнейшем, приводя конкретные числовые примеры, мы
отказываемся от использования двоичной арифметики. Десятичная
арифметика привычнее, а основные закономерности поведения ошибок
округления не зависят от основания используемой системы. В боль­
щинстве расчетов, которые будут приведены для иллюстрации поведе­
ния ошибок округления, имитируется выполнение вычислений на гипо­
тетическом компьютере, имеющем шесть десятичных разрядов
мантиссы и производящем округление по дополнению. Будем называть
этот компьютер 6-разрядным десятичным компьютершt. Для него Ем=
= 5 · 10-7, так что по точности он сравним со стандартным компьюте­
ром (при вычислениях с одинарной точностью).
7. Дополнительные сведения об IEEE арифметике. Напомним,
что кроме нормализованных чисел IEEE арифметика включает в себя
субнормальные (денормализованные) числа. В отличие от нормализо­
ванных чисел в представлении (2.26) для субнормальных чисел всегда
у1 =О ир = Pmin· Субнормальные числа расположены в интервале (-Х0,Х0).
Расстояние между двумя соседними субнормальными числами посто­
янно. В арифметике обычной точности оно составляет 2-150 ~ 10-45, а в
арифметике двойной точности 2-1075 ~ 10-324.
Одним из приятных следствий наличия субнормальных чисел явля­
ется тот факт, что в IEEE арифметике равенство х е у = О возможно
тогда и только тогда, когда х = у.
Множество нормализованных и субнормальных чисел в IEEE ариф­
метике дополнено символами +ао, -оо и NaN (Not а Number -
НеЧисло). Символы ±ао генерируются в случае, если при выполнении
очередной операции возникает переполнение. Символы ±ао представля-
45

47. Глава 2. Введение в элементарную теорию погрешностей
ются в виде (2.26) с нулевой мантиссой и показателем р =Ртах + l,
т.е. в виде
±оо =±(О.ООО ... О)· 2
Ртах+ 1
Символы ±сх:> ведут себя в соответствии со следующими естествен-
х
ными правилами: +сх:>+оо = +сх:>, (-l)x(+cx:>) = --<X.J, - =О для всякого
±00
+оо
числа х с плавающей точкой, =-- =±сх:> для всякого положительного
х
числах с плавающей точкой, +сх:> ЕВ х = +сх:> и т.д.
Символ NaN генерируется в случае, если результат выполняемой
операции не определен. Например 5= NaN, Д = NaN, Ох(+сх:>) = NaN,
00
+сх:> + (--СХ>) = NaN, ;;;; = NaN, NaN ЕВ х = NaN, NaN е NaN = NaN и т.д.
NaN числа представляются в виде (2.26) с ненулевой мантиссой и с
показателем р =Ртах + l.
Таким образом, IEEE арифметика замкнута относительно арифмети­
ческих операций. Каждая выполняемая на компьютере операция имеет
результатом либо число с плавающей точкой, либо один из символов
+сх:>, --<X.J, NaN. Информация о возникновении символов ±сх:> или NaN
доводится до сведения пользователя выставлением индикатора особого
случая (exception flag), но работа программы при этом не прерывается.
Это позволяет разрабатывать более надежные программы. Любые два
NaN числа считаются различными. Поэтому простейший способ убе­
диться в том, что х =NaN состоит в проверке свойства х *х.
Замечание. Казалось бы, результат выполнения операции о0 в
IEEE арифметике должен получить значение NaN, но в дей­
ствительности принято соглашение, что о0 = l. Это соглашение
очень полезно при работе с многочленами.
§ 2.6. Допоnнитеnьные замечания
1. Более подробно приближенные числа и погрешности арифмети­
ческих операций над ними изложены в известном учебном пособии
[35]. Здесь же приведены правила подсчета оставляемых значащих
цифр, которые рекомендуется применять при массовых «ручных»
вычислениях без точного учета погрешностей.
46

48. § 2.6. Дополнительные замечания
2. Дополнительную информацию об особенностях арифметических
операций над числами с плавающей точкой можно найти, например
в (23, 54, l02, 106].
3. В последнее время в практике вычислений в качестве меры
погрешности приближенного числа а• часто используют величину
1а -1а*11, объединяющую в себе черты абсолютной и относительной
1 + а
погрешностей. Она близка к Л(а*) при 1а1 « l и практически совпа­
дает с 15(а*) при 1а1 » 1.
4. Информацию о IEEE стандарте можно найти в [54, 122, 5*, 15*,
20•, 24*].
5. Для уменьшения погрешностей округления иногда используется
рациональная арифметика. В ней каждое рациональное число пред­
ставляется парой целых чисел (с увеличенным по сравнению со стан­
дартным числом разрядов) - числителем и знаменателем. Арифмети­
ческие операции над такими числами производятся как над обычными
рациональными дробями.
Рациональная арифметика реализована во многих пакетах символь­
ных вычислений, например в пакетах Mathematica и MACSYMA.
6. К настоящему времени разработан интервальный анализ, даю­
щий возможность заставить компьютер следить за совершаемыми
ошибками округления, чтобы затем получить гарантированные оценки
их накопления.
47

49. Глава 3
ВЫЧИСЛИТЕЛЬНЫЕ ЗАДАЧИ, МЕТОДЫ
И АЛГОРИТМЫ. ОСНОВНЫЕ ПОНЯТИЯ
§ 3.1. Корректность вычисnитеnьной задачи
1. Постановка вычислительной задачи. Под вычислительной
задачей будем понимать одну из трех задач, которые возникают при
анализе математических моделей: прямую задачу, обратную задачу или
задачу идентификации (см. § 1.2). Слово «вычислительная» подчерки­
вает, что основные усилия будут направлены на то, чтобы найти
(вычислить) ее решение.
Будем считать, что постановка задачи включает в себя задание мно­
.жества допустимых входных данных Х и множества возможных
решений У. Цель вычислительной задачи состоит в нахождении реше­
ния у е У по заданному входному данному х е Х. Для простоты пони­
мания достаточно ограничиться рассмотрением задач, в которых вход­
ные данные и решение могут быть только числами, наборами чисел
(векторами, матрицами, последовательностями) и функциями. Предпо­
ложим, что для оценки величин погрешностей приближенных входных
данных х" и приближенного решения у" введены абсолютные и относи-
тельные погрешности Л(х"), Л(у"), cS(x"), о(у"), а также их границы Л(х"),
Л(у"), Б(х"), б(у"). Определения этих величин когда х и у - числа,
были даны в § 2.2. В тех случаях, когда входные данные или решение не
являются числами, эти характеристики погрешностей также можно вве­
сти естественным образом; мы будем это делать по мере необходимости.
2. Определение корректности задачи. Анализ важнейших требо­
ваний, предъявляемых к различным прикладным задачам, приводит
к понятию корректности математической задачи, которое было впервые
сформулировано Ж. Адамаром 1 и развито затем И.Г. Петровским 2•
Вычислительная задача называется корректной (по Адамару-Петров­
скому), если выполнены следующие три требования:
1) ее решение у е У существует при любых входных данных х е Х;
1 Жак Адаtар (1865-1963) - французский математик.
2 Иван Георгиевич Петровский (1901-1973) - российский математик.
48

50. § 3.1. Корректность вычислительной задачи
2) это решение единственно;
3) решение устойчиво по отношению к малым возмущениям вход­
ных данных.
В том случае, когда хотя бы одно из этих требований не выполнено,
задача называется некорректной.
Существование решения вычислительной задачи - естественное
требование к ней. Отсутствие решения может свидетельствовать,
например, о непригодности принятой математической модели либо о
неправильной постановке задачи. Иногда отсутствие решения является
следствием неправильного выбора множества допустимых входных
данных Х или множества возможных решений У.
Пр и мер 3.1. Рассмотрим задачу о решении квадратного уравнения
х2 + Ьх + с = О. (3.1)
Старший коэффициент а считается равным единице; этого всегда можно
добиться делением уравнения на а. Если считать входным данным пару
коэффициентов Ь, с и искать решение в множестве вещественных чисел,
то существование решений
х1 = (-b-Jb2 -4c)/2, х2 = (-Ь+ Jь2 -4с)/2 (3.2)
будет гарантировано только в том случае, если ограничить множе­
ство входных данных коэффициентами, удовлетворяющими условию
Ь2 - 4с ~ О. Если же расширить множество возможных решении и счи­
тать, что корни (3.2) могут принимать комплексные значения, то задача
будет иметь решение при любых Ь, с. .А.
Так как математическая модель не является абсолютно точным
отражением реальной ситуации, то даже в случае, когда исходная про­
блема заведомо имеет решение, соответствующая вычислительная
задача может и не оказаться разрешимой. Конечно, такая ситуация
говорит о серьезном дефекте в постановке задачи. Иногда отсутствие
решения математической задачи приводит к пониманию того, что пер­
воначально сформулированная проблема неразрешима и нуждается
в серьезной корректировке.
3. Единственность. Для некоторых вычислительных задач единст­
венность является естественным свойством; для других же решение
может и не быть единственным. Например, квадратное уравнение (3.1)
имеет два корня (3.2). Как правило, если задача имеет реальное содер­
жание, то неединственность может быть ликвидирована введением
дополнительных ограничений на решение (т.е. сужением множества У).
В некоторых случаях проблема снимается тем, что признается целесо­
образным найти набор всех решений, отвечающих входным данным х,
49

51. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
и тогда за решение у принимается этот набор. Например, для уравнения
(3.) решением можно назвать пару (х 1 , х2 ).
Неединственность решения вычислительной задачи - весьма
неприятное свойство. Оно может быть проявлением неправильной
постановки исходной прикладной проблемы, неоднозначности ее реше­
ния или сигналом о неудачном выборе математической модели.
4. Устойчивость решения. Решение у вычислительной задачи
называется устойчивым по входным данным х, если оно зависит от
входных данных непрерывным образом. Это означает, что для любого
Е >О существует 8 = 8(Е) >О такое, что всякому исходному данному х",
удовлетворяющему условию Л(х*) < 8, отвечает приближенное решение
у*, для которого Л(у*) < Е. Таким образом, для устойчивой вычислитель­
ной задачи ее решение теоретически можно найти со сколь угодно
высокой точностью Е, если обеспечена достаточно высокая точность 8
входных данных. Схематически ситуация изображена на рис. 3.1. Мно­
жества тех х• и у*, для которых Л(х") < 8 и Л(у") < Е изображены как
окрестности точек t и у имеющие радиусы 8 и Е. Требование увеличить
точность решения приводит автоматически к повышению требований
к точности данных; соответствующие окрестности на рис. 3.1 отмечены
штрихами.
Неустойчивость решения у означает, что существует такое i:0 > О,
что какое бы малое 8 > О ни было задано, найдутся такие исходные дан­
ные х", что Л(х0 ) < 8, но Л(у*):?: в 0 .
Приведем простейшие примеры устойчивых и неустойчивых задач.
Пр им ер 3.2. Задача вычисления корней квадратного уравнения
(3.1) устойчива, так как корни (3.2) являются непрерывными функ­
циями коэффициентов Ь и с. А
Рис. 3.1
50

52. § 3.1. Корректность вычислительной задачи
Пр и мер 3.3. Задача о вычислении ранга матрицы в общем случае
неустойчива. В самом деле, для матрицы А = [ ~ ~] ранг равен 1,
поскольку det А = О и существует ненулевой элемент а11 = 1. Однако сколь
угодно малое возмущение коэффициента а22 на величину Е * О приводит
к матрице Аt = [~ ~] , для которой detA t = Е *О и, следовательно, ранг
равен 2. А
Пр им ер 3.4. Покажем, что задача вычисления определенного
ь
интеграла/= ffi.x) dx устойчива.
а
Пусть /*(х) - приближенно заданная интегрируемая функция и
ь
/* = ff*(x) dx. Определим абсолютную погрешность функции/* с
а
помощью равенства Л(/*} = sup lf(x)-/*(x}I, в котором знак sup
хе [а,Ь]
можно заменить на max, если f и /* непрерывны. Так как
ь
Л(/*)= IJ-J*I = lf(f(x)-/*(x))dxl ~(Ь-а)Л(/*}, (3.3)
а
то для любого Е >О неравенство Л(/*) < Е будет выполнено, если потре­
бовать выполнение условия Л(/*) < S = El(b - а). .&
Пример 3.5. Покажем, что задача вычисления производной
и(х) = f'(x) приближенно заданной функции является неустойчивой.
Пусть/*(х)- приближенно заданная на отрезке [а, Ь] непрерывно
дифференцируемая функция и и*(х) = (/*)'(х). Определим абсолютные
погрешности с помощью равенств
Л(/*) = maxl /(x}-/*(x)I,
[а,Ь]
Л(и*) = maxl и(х)- u*(x)I.
[a,h]
Возьмем, например/*(х) = /(х) + аsш(х/а2 ), где О< а« .Тогда
и*(х) = и(х) + а- 1 cos(x /а2) и Л(и*) = а- 1 , в то время как Л(/*) = а.
Таким образом, сколь угодно малой погрешности задания функции f
может отвечать сколь угодно большая погрешность производной f'. .&
51

53. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
у
о а
~//1 ["(х)
1 /(х)
JJШШl'-nm.,-~"'. А
----~~ :
Рис. 3.2
1
1
1
1
1
1
1
1
ь х
Различие в ситуациях, возникающих при приближенном задании
функции/в задачах интегрирования и дифференцирования, отражено
на рис. 3.2. Видно, что уменьшение значения б = Л(j*) влечет за собой
уменьшение погрешности Л(j*) (ее значение не превышает заштрихо­
ванной площади), в то время как производные f' и (j* )' могут отли­
чаться сколь угодно сильно.
Одна и та же задача может оказаться как устойчивой, так и неустой­
чивой в зависимости от выбора способа вычисления абсолютных
погрешностей Л(х*) и Л(у*). В реальных задачах этот выбор определя­
ется тем, в каком смысле должно быть близко приближенное решение
к точному и малость какой из мер погрешности входных данных
можно гарантировать.
Пр им ер 3.6. Рассмотрим задачу о вычислении суммы сходящегося
00
ряда S = Lak с приближенно заданными слагаемыми а; :::: ak. Если а;
k=O
определяется таким образом, что гарантируется малость Л (а; ) для всех k,
• • 00 •
то для последовательности а = { ak} k=O естественно положить Л (а ) =
= supj ak - a;J. В такой постановке задача неустойчива. Чтобы убедиться
k~O
в этом, достаточно положить а; = ak + б (где б >О) для k < N и а; = ak
00
для k ~ N. Тогда ДЛЯ суммы ряда s· = Lа; имеем Л(S*) = N б. Следо­
k=О
вательно, как бы ни была мала величина Л(а*) = о, абсолютную
ПОГреШНОСТЬ суммы ряда S* С ПОМОЩЬЮ выбора N МОЖНО сделать СКОЛЬ
52

54. § З. 1. Корректность вычислительной задачи
угодно большой. Если же положить а; = ak + о для всех k, то сумма
ряда s• вообще станет бесконечной, т.е. ряд станет расходящимся.
В то же время, если можно задавать а; так, чтобы оказалась малой
00
величина Л(а*} = L 1 аА - а; 1 • то Л(S *) =
k=O
такой постановке задача устойчива. .А.
00
1L(ak-a;)I $ Л(а*) и в
k=O
5. Относительная устойчивость решения. Часто требование
малости абсолютной погрешности является неоправданным или трудно
проверяемым. В таких случаях полезно рассмотреть относительную
устойчивость решения, определение которой отличается от данного
выше определения устойчивости (абсолютной устойчивости) только
тем, что Л(х") и л(у•) заменяются на о(х•) и о(у•) соответственно.
00
Пример 3.7. Вернемся к задаче вычисления суммы ряда S = Lak
k=O
из примера 3.6. Предположим, что ak -t:. О для всех k. Часто можно
гарантировать малость величины о(а•)= sup{jak-a;J!lakl}. Тогда
k20
00
Л(а;) $ lakl ·о(а·) и поэтому Л(S.) $ L 1akl. о(а·). Таким образом,
k=O
o(S°) $ (f1akl/1fak1) о(а•). (3.4)
k=O k=O
Следовательно, задача вычисления суммы сходящегося ряда S
относительно устойчива, если он сходится абсолютно (т.е. сходится
00
ряд L 1 akl ). Если же ряд сходится только условно, т.е.
k=O
то задача не является относительно устойчивой . .А.
00
= 00
'
Замечание. Так как для решения вычислительных задач
используют компьютеры, точность которых определяется разряд­
ностью мантиссы или эквивалентным значением границы относи­
тельной погрешности округления Е", то представляется более
естественным исс,1едование относительной устойчивости.
6. О некорректных задачах. Длительное время считалось, что некор­
ректные задачи, решения которых неустойчивы, не имеют физического
смысла и не представляют ценности для приложений. Однако это мне­
ние оказалось ошибочным. Как выяснилось, многие важные приклад-
53

55. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
ные задачи некорректны. Не вызывает, например, сомнения практиче­
ская важность решения некорректных задач дифференцирования и
суммирования ряда (см. примеры 3.5., 3.6). К некорректным задачам
относятся также обратные задачи геофизики, астрофизики, спектрогра­
фии, многие задачи распознавания образов, задачи синтеза и ряд дру­
гих прикладных задач.
К настоящему времени разработана теория решения многих классов
некорректных задач. Важная роль в создании методов решения таких
задач принадлежит российским математикам, в первую очередь
А.Н. Тихонову 1 • Эти методы (методы регуляризации) довольно сложны
и выходят за рамки данной книги. Мы ограничимся изложением в
§ 16.7 того, как метод регуляризации может быть применен в случае
некорректной задачи вычисления решения интегрального уравнения
Фредгольма первого ряда. Для первого знакомства с методами регуля­
ризации можно рекомендовать учебные пособия (37, 97].
§ 3.2. Обусловленность вычислительной задачи
1. Определения. Пусть вычислительная задача корректна (ее
решение существует, единственно и устойчиво по входным данным).
Теоретически наличие у задачи устойчивости означает, что ее реше­
ние может быть найдено со сколь угодно малой погрешностью, если
только гарантировать, что погрешности входных данных достаточно
малы. Однако на практике погрешности входных данных не могут быть
сделаны сколь угодно малыми, точность их ограничена. Даже то что
исходные данные нужно будет ввести в компьютер, означает, что их
относительная точность будет заведомо ограничена величиной порядка
Ем (см. § 2.5). В реальности, конечно, уровень ошибок в исходной
информации будет существенно выше. Как же повлияют малые, но
конечные погрешности входных данных на решение, как сильно спо­
собны они исказить желаемый результат? Для ответа на этот вопрос
введем новые понятия.
Под обусловленностью вычислительной задачи понимают чувстви­
тельность ее решения к малым погрешностям входных данных. Задачу
называют хорошо обусловленной, если малым погрешностям входных
данных отвечают малые погрешности решения, и плохо обусловленной,
если возможны сильные изменения решения.
Часто оказывается возможным ввести количественную меру степени
обусловленности вычислительной задачи - число обусловленности.
Эту величину можно интерпретировать как коэффициент возможного
1 Андрей Николаевич Тихонов (1906-1993) - российский математик, один из созда­
телей теории решения некорректных задач.
54

56. § 3.2. Обусловленность вычислительной задачи
возрастания погрешностей в решении по отношению к вызвавшим их
погрешностям входных данных.
Пусть между абсолютными погрешностями входных данных х и
решения у установлено неравенство
Л(v0 ) ~ vлЛ(х0). (3.5)
Тогда величина vл называется абсолютным числом обусловленности.
Если же установлено неравенство
(3.6)
между относительными погрешностями данных и решения, то вели­
чину v0 называют относительным числом обусловленности. В неравен­
ствах (3.5), (3.6) вместо погрешностей Л и 8 могут фигурировать их
границы Л и 8 . Обычно под числом обусловленности v задачи пони­
мают одну из величин vл или v0, причем выбор бывает ясен из смысла
задачи. Чаще все же под числом обусловленности понимают относи­
тельное число обусловленности. Для плохо обусловленной задачи v » 1.
В некотором смысле неустойчивость задачи - это крайнее проявление
плохой обусловленности, отвечающее значению v = оо. Конечно, v -
это максимальный коэффициент возможного возрастания уровня оши­
бок, и для конкретных входных данных действительный коэффициент
возрастания может оказаться существенно меньше. Однако при выводе
оценок (3.5) и (3.6) стремятся к тому, чтобы не завышать значений vл
и v0 и поэтому соотношение v >> 1 все же свидетельствует о реальной
возможности существенного роста ошибок. Грубо говоря, если v - JON,
где v - относительное число обусловленности, то порядок N показы­
вает число верных цифр, которое может быть утеряно в результате по
сравнению с числом верных цифр входных данных.
Каково то значение v, при котором следует признать задачу плохо
обусловленной? Ответ на этот вопрос существенно зависит, с одной сто­
роны, от предъявляемых требований к точности решения и, с другой -
от уровня обеспечиваемой точности исходных данных. Например, если
требуется найти решение с точностью 0.1 %, а входная информация
задается с точностью 0.02 %, то уже значение v = 1О сигнализирует
о плохой обусловленности Однако (при тех же требованиях к точности
результата) гарантия, что исходные данные задаются с точностью не
ниже 0.0001 %, означает, что и при v = 103 задача хорошо обусловлена.
С простым, но очень важным примером плохо обусловленной
задачи мы уже познакомились в § 2.3. Это задача вычитания прибли­
женных чисел одного знака. Оценка (2.10) дает для нее значение отно­
сительного числа обусловленности v = 1а + Ь 1/1 а - Ь 1. Так как в при-
55

57. Глава З. Вычислительные задачи, методы и алгоритмы. Основные понятия
мере 2.11 имеем v"" J1+x*l!J1 - x•I ""7 · 105, то потеря пяти верных
значащих цифр здесь не представляется удивительной.
2. Примеры плохо обусловленных задач. Первым рассмотрим
классический приМJ:р, принадлежащий Дж. Уилкинсону 1 [102].
Пр им ер 3.8. Пусть требуется найти корни многочлена
P(x)=(x- l)(x-2) ... (х-20)=х20_21Ох19+ ...
по заданным значениям его коэффициентов. Из теории известно, что
эта задача устойчива. Возьмем коэффициент а= -210 при х 19 и изме­
ним его значение на а• = -21 О + 2-23• Как повлияет эта, казалось бы,
незначительная погрешность на значения корней? Заметим, что х 1 = 1,
х2 = 2, .. " х20 =20 - точные значения корней.
Вычисленные с высокой точностью корни возмущенного много­
члена таковы:
х; "" 1.00000, х; "" 2.00000, х; "" 3.00000, х; "" 4.00000,
х; ""5.00000, х~ ""6.00001, х; ""6.99970, х; ""8.00727,
х; "" 8.91725, х;0, 11 "" 10.0953 ± 0.643501 i, х;2, 13 "" 11.7936 ± l.65233i,
х;4, 15 ""13.9924±2.51883i, х;6, 17 ""16.7307±2.81262i,
х;8, 19 "" 19.5024 ± 1.94033i, х;0 ""20.8469.
Как нетрудно видеть, корни х1 , ••• , х6 оказались практически нечувстви­
тельны к погрешностям в коэффициенте а. В то же время некоторые
корни превратились в комплексные и имеют относительные погрешно­
сти ОТ 6 ДО 18 %, несмотря на ТО, ЧТО О(а•) "" 6 • 1О-8 %.
В данном случае нетрудно провести анализ чувствительности кор­
ней. Пусть F(x, а) = х20 + ах 19 + .... Будем рассматривать корни xk как
функции параметра а, т.е. xk = xk(a). Равенство F(xk(a), а)= О, выпол­
ненное в окрестности точки а = -21 О, задает xk как неявную функцию
от а. Пользуясь второй из формул (2.22) для границы относительной
погрешности и применяя формулу (2.23) для производной неявной
функции, имеем
1 Джеймс Х. Уилкинсон (1918-1986) - американский математик, внесший значи­
тельный вклад в современное пони'llание вычислительных методов. О деятельности
Джеймса Х. Уилкинсона см. (54].
56

58. § 3.2. Обусловленность вычислительной задачи
ial · IF~/F~i 1
где vk = 1 1
Х x=xk, а=-210
Учитывая, что
дF = х19
да
и
aFJ 20 20 20
дх =P'(x)lx=k = L ТТ (х - i)lx=k = ТТ (k- i) •
x=k, а=-210 j= J /·=~ IJ..=~
получаем
20k 18
v"= 20
Пlk-i
/= 1
i"'k
'"'j i "'k
Вычисление чисел vk дает следующие значения:
v1:::::2·0-15, v2 :::::9·10-8, v3 :::::10-4, v4 :::::0-1, v5 :::::3·01,
v6 :::::2·103, v7 :::::8•104, v8 :::::2·106, v9 :::::2·107, v10 :::::2·108,
Vll ::::: 9 • 109, v12 ::::: 4 • 09, v13 ::::: 1010, v14 ::::: 2 • 1010,
V15::::: 3 • 1010, v16 ::::: 3 • 1010, v17 ::::: 3 • 1010, v18 ::::: 010,
v19 :::::3·109, v20 :::::5•108,
свидетельствующие о чрезвычайно плохой обусловленности старших
корней. А
Следует обратить серьезное внимание на то, что задача вычисления
корней многочленов высокой степени часто оказывается плохо обу­
словленной. Поэтому имеет смысл с определенной настороженностью
относиться к алгоритмам, составной частью которых является вычисле­
ние корней многочленов высокой степени.
К сожалению, эта задача может быть плохо обусловленной и для
многочленов невысокой степени, в особенности, если вычисляются
кратные корни.
Пр им ер 3.9. Пусть ищется решение уравнения (х - 1)4 = О с крат­
ным корнем. Погрешность в младшем коэффициенте, равная 10-8, приво­
дит к уравнению (х - 1)4 = 10-8, имеющему следующие корни: х1 , 2 =
= 1±10-2, х3, 4 = 1 ± 10-2 • i. В этом случае погрешность, равная 10-6 %
в одном из коэффициентов, привела к погрешности решения примерно
в 1 %, что явно говорит о плохой обусловленности задачи. А
57

59. Глава З. Вычислительные задачи, методы и алгоритмы. Основные понятия
3. Обусловленность задачи вычисления значения функции
одной переменной. Пусть задача состоит в вычислении по заданному х
значения у = j(x) дифференцируемой функции f В силу формул (2.21 ),
(2.22) для этой задачи имеем:
Ул== l/'(x)I, (3.7)
lxl · lf'(x)I
V.s"" lf(x)I (3.8)
Воспользуемся этими формулами для оценки обусловленности
задачи вычисления значений некоторых элементарных функций.
Пр им ер 3.1О. Для задачи вычисления значения функции у = еХ в
силу формулы (3.8) относительное число обусловленности v0 прибли-
женно равно 1х1 и при реальных вычислениях оно не может быть очень
большим. Например, при вычислении экспоненты на компьютере типа
IВМ РС всегда 1х1 ::5 88, так как в противном случае возможно пере­
полнение или антипереполнение. Следовательно, задача вычисления
этой функции хорошо обусловлена, однако в случае 1О < /х / < 102 сле­
дует ожидать потери одной-двух верных значащих цифр по сравнению
с числом верных цифр аргумента х. Подчеркнем, что эта потеря точно­
сти объективно обусловлена погрешностью задания аргумента и не
связана с используемым алгоритмом. .&
Пр им ер 3.11. Для задачи вычисления значения функции у = sinx
в силу формулы (3.7) имеем vл = /cosx / ~ 1, что говорит о хорошей
абсолютной обусловленности этой задачи при всех х. Однако если
важен результат с определенным числом верных знаков, то нужно
исследовать относительную обусловленность. Согласно формуле
(3.8) имеем v0 == lx ctgx 1. На рис. 3.3 приведен график этой функ­
ции при х ~ О (она четная).
Так как v0 --+ оо при х -> тт k (для k = ± 1, ±2, ...), то при х == ттk задача
обладает плохой относительной обусловленностью, и можно лишь уте­
шаться тем, что мала абсолютная погрешность значения у• = sinx•.
Если же значение lxl очень велико, то v0 >> 1 и вычислять значение
синуса просто бессмысленно. Например, если вычисления ведутся на
компьютере типа IВМ РС, где &м - 10-7 при вычислениях с одинарной
точностью, то уже для 1х1 - 107 одна только абсолютная погрешность
представления числах есть величина порядка единицы, так как Л(х*) ==
== lxl ·Ем. Нетрудно понять, что при Л(х*) - 1 вычисленное любым
способом значение sinx• не представляет никакой ценности. Вывод,
58

60. § 3.2. Обусловленность вычислительной задачи
у
О 1t/2 1t З1t/2 21t 51t/2 З1t х
Рис. 3.3
который можно сделать, довольно прост: при использовании функции
у = sinx желательно проводить вычисления так, чтобы аргумент нахо­
дился в диапазоне 1х1 < 2, поскольку здесь v0 ~ 1. А
ь
4. Обусловленность задачи вычисления интеграла/= fЛх) dx.
а
Как следует из оценки (3.3), в этом случае абсолютное число обуслов­
ленности имеет вид vл = Ь - а. Если же перейти к рассмотрению отно-
сительных погрешностей и положить fJ(f*) = sup l/*(x)-f(x)l!if(x)I
(а, Ь]
для тех, х, где /(х) *О, то используя неравенство
ь h
Л(/*) ~ ЛJ*(x)-f(x)I dx ~ JIЛx)I dx •fJ(j),
а а
получаем оценку
(3.9)
ь ь
в которой v0 = flf(x) 1dx /1 JЛх) dx 1.
а а
Если подынтегральная функция знакопостоянна, то v0 = 1 и задача
хорошо обусловлена. Если же функция f на отрезке [а, Ь] принимает
значения разных знаков, то v0 > 1. Для некоторых сильно колеблю-
щихся (осциллирующих) около нуля функций может оказаться, что
v0 » 1 и тогда задача вычисления интеграла является плохо обуслов-
ленной.
59

61. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
Иногда причиной появления плохо обусловленных задач становится
отсутствие у пользователя компьютера элементарного представления
об их существовании. В связи с этим заметим, что в последнее время
получила развитие опасная тенденция пренебрежительного отношения
к математическим знаниям вообще и к знанию вычислительной мате­
матики, в частности. Вера в могущество компьютеров и надежность
стандартных программ бывает так велика, что считается совсем ненуж­
ным знать о вычисляемой математической величине что-либо кроме ее
определения и, возможно, геометрического или физического смысла.
Приведем простой пример, иллюстрирующий оценку (3.9) и заодно
показывающий, что иногда аналитическая выкладка бывает эффектив­
нее, чем применение самого современного компьютера.
Пр им ер 3.12. Пусть в распоряжении пользователя имеется высо­
копроизводительный компьютер и стандартная программа для вычис­
ь
ления интегралов вида 1 = jf(x) dx. Предположим, что нужно вычис-
а
1
лить коэффициенты Фурье gn = jg(x) sin(лnx) dx для функции g(x) =
-1
2
= х + А ecos х при п » 1 и А » 1. Использование для вычисления gn
указанной стандартной программы при /(х) = g(x) siп(л nx) автоматиче­
ски означает, что ставится вычислительная задача, рассмотренная
выше. При этом относительная погрешность Ы/*) вычисляемой на ком­
пьютере функции .f :::о/заведомо не может быть меньше1 Ем.
Оценим величину v0. Заметим, что функция А ес0•2х siп(л пх) нечет­
ная и, следовательно, интеграл от нее равен нулю. Поэтому возможно
аналитическое вычисление интеграла:
1 ~ 1 1 1 2
gn= Jxsiп(лnx)dx=--cos(лnx)J +- Jcos(лnx)dx=-(-J)n+1.
- 11п _1 лп_ 1 лп
Кроме того, jg(x)j ~ 1Аec0s2x1 - lxl ~А - 1 и поэтому
1 1 1
jlf(x)I dx= Ji g(x)I · 1 sin(лnx)I dx ~(А - 1) JI sin(лnx)I dx =А - 1.
-1 -1 -
1Если учитывать погрешность вычисления функции sin(л пх), то с,1едует ожидать. что
па погрешность будет значительно бо,1ьше Е ,...
60

62. § 3.3. Вычислительные методы
Таким образом, v15 ~ (А - 1)rtn/2 ~ .5Ап. Если g" вычисляется, напри­
мер при А= 104 и п = 102, то v15 ~ 1.5 · 106. Следовательно, для этих зна­
чений параметров принятое решение о вычислении интеграла по про­
стейшей стандартной программе может обойтись в потерю примерно
шести значащих цифр результата. Если вычисления ведутся на компью­
тере, имеющем лишь около семи десятичных значащих цифр, то воз­
можна катастрофическая потеря точности. Заметим, что в этих рассужде­
ниях никак не учтены погрешность реализованного в программе метода
и вычислительная погрешность, наличие которых усугубляет ситуацию. •
5. Обусловленность задачи вычисления суммы ряда. Рассмот­
рим задачу вычисления суммы абсолютно сходящегося ряда с ненуле­
выми слагаемыми. В силу оценки (3.4) эта задача устойчива, а за отно­
сительное число обусловленности следует принять величину
00 00
V15 = L lakl /1 Lakl · (3.1 О)
k=O k=O
Заметим, что для ряда с положительными слагаемыми имеем v15 = l,
т.е. задача хорошо обусловлена. Если же ряд незнакопостоянный, то
v15 > 1 и при v15 » 1 задача оказывается плохо обусловленной.
§ 3.3. Вычисnитеnьные методы
Обсудив некоторые важные особенности вычислительных задач,
обратим внимание на те методы, которые используются в вычисли­
тельной математике для преобразования задач к виду, удобному для
реализации на компьютере, и позволяют конструировать вычислитель­
ные алгорит"1ы. Мы будем называть эти методы вычислительными.
С некоторой степенью условности можно разбить вычислительные
методы на следующие классы:
1) методы эквивалентных преобразований;
2) методы аппроксимации;
3) прямые (точные) методы;
4) итерационные методы;
5) методы статистических испытаний (методы Монте-Карло).
Метод, осуществляющий вычисление решения конкретной задачи,
может иметь довольно сложную структуру, но его элементарными
шагами, являются, как правило, реализации указанных методов. Дадим
о них общее представление.
1. Методы эквивалентных преобразований. Эти методы позво­
ляют заменить исходную задачу другой, имеющей то же решение.
61

63. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
Выполнение эквивалентных преобразований оказывается полезным,
если новая задача проще исходной или обладает лучшими свойствами,
или для нее существует известный метод решения, а, может быть, и
готовая программа.
Пр им ер 3.13. Эквивалентное преобразование квадратного уравнения
( ь) 2 ь2 -4с
х2 + Ьх +с= О к виду х + 2 = - 4- (выделение полного квадрата)
сводит задачу к проблеме вычисления квадратного корня и приводит
к известным для ее корней формулам (3.2). •
Эквивалентные преобразования иногда позволяют свести решение
исходной вычислительной задачи к решению вычислительной задачи
совершенно иного типа.
Пр им ер 3.14. Задача отыскания корня нелинейного уравнения
/(х) = О может быть сведена к эквивалентной задаче поиска точки гло­
бального минимума функции Ф(х) = (f(x))2. В самом деле, функция
Ф(х) неотрицательна и достигает минимального значения, равного
нулю, при тех и только тех х, для которых /(х) =О. •
2. Методы аппроксимации. Эти методы позволяют приблизить
(аппроксимировать) исходную задачу другой, решение которой в опре­
деленном смысле близко к решению исходной задачи. Погрешность,
возникающая при такой замене, называется погрешностью аппрокси­
мации. Как правило, аппроксимирующая задача содержит некоторые
параметры, позволяющие регулировать значение погрешности аппрок­
симации или воздействовать на другие свойства задачи. Принято гово­
рить, что метод аппроксимации сходится, если погрешность аппрокси­
мации стремится к нулю при стремлении параметров метода к
некоторому предельному значению.
Пр им ер 3.15. Один из простейших способов вычисления инте­
ь
грала / = ff(x) dx состоит в аппроксимации интеграла на основании
а
формулы прямоугольников величиной
Jh = hff(a+(1-~)h).
1~1
Шаг h= (Ь - а)/п является здесь параметром метода. Так как Jh пред­
ставляет собой специальным образом построенную интегральную
62

64. § 3.3. Вычислительные методы
сумму, то из определения определенного интеграла следует, что Jh - 1
при h - О, т.е. метод прямоугольников сходится. .А.
Пример 3.16. Учитывая определение производной функции
f(x +h)-f(x)
f'(x) = lrm h , для ее приближенного вычисления можно
h - о
/(т + h)-f(x)
использовать формулу/' (х) "' h . Погрешность аппроксима-
ции этой формулы численного дифференцирования стремится к нулю
при h - О. .А.
Одним из распространенных методов аппроксимации является дис­
кретизация - приближенная замена исходной задачи конечномерной
задачей, т.е. задачей, входные данные и искомое решение которой
могут быть однозначно заданы конечным набором чисел. Для задач,
которые не являются конечномерными, этот шаг необходим для после­
дующей реализации на компьютере, так как вычислительная машина в
состоянии оперировать лишь с конечным количеством чисел. В приве­
денных выше примерах 3.15 и 3.16 была использована дискретизация.
Хотя точное вычисление интеграла и предполагает использование бес­
конечного множества значений f(x) (для всех х Е [а, Ь]), его прибли­
женное значение можно вычислить, использовав конечное число п зна­
чений в точках а + (i -l/2)h. Аналогично, задача вычисления
производной, точное решение которой предполагает выполнение опе­
рации предельного перехода при h - О (а следовательно, использова­
ние бесконечного множества значений функции/), сводится к прибли­
женному вычислению производной по двум значениям функции.
При решении нелинейных задач широко используют различные
методы линеаризации, состоящие в приближенной замене исходной
задачи более простыми линейными задачами.
Пр им ер 3.17. Пусть требуется приближенно вычислить значение х =
= Га для а > О на компьютере, способном выполнять простейшие ариф­
метические операции. Заметим, что по определению х = Ja является
положительным корнем нелинейного уравнения х 2 - а= О. Пусть x<0J-
некоторое известное приближение к Ja Заменим параболу у= х2 - а пря­
мой у= (x<OJ )2- а + 2х<О>(х - х<О>), являющейся касательной, проведенной
к ней в точке с абсциссой х = x<OJ (рис. 3.4). Точка пересечения этой каса­
тельной с осью Ох дает лучшее, чем x<0J, приближение и находится из
63

65. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
Рис. 3.4
линейного уравнения (х<0>)2 - а + 2х<0>(х - х<0>) = О. Решая его, полу­
чаем приближенную формулу
Ja ""х• = х<О) - (х<О>)2 - а=! (х<О) + ...!!....) .
2.л (О) 2 х<О)
(3. 11)
Например, если для х = J2 взять х<0> = 2, то получится уточненное
значение J2 zx• = ~ (2 + ~) = 1.5. А
При решении разных классов вычислительных задач могут исполь­
зоваться различные методы аппроксимации; к ним можно отнести и
методы регуляризации решения некорректных задач. Заметим, что
методы регуляризации широко используют для решения плохо обу­
словленных задач.
3. Прямые методы. Метод решения задачи называют прямым, если
он позволяет получить решение после выполнения конечного числа
элементарных операций
Пр им ер 3.18. Метод вычисления корней квадратного уравнения
х2 + Ьх +с= О по формулам х 1 , 2 = (- Ь ± JЬ2 - 4с) /2 является прямым
методом. Элементарными здесь считаются четыре арифметические
операции и операция извлечения квадратного корня. А
Замети!, что элементарная операция прямого метода может ока­
заться довольно сложной (вычисление 1начений элементарной или спе­
циальной функции, решение системы линейных алгебраических урав-
64

66. § 3.3. Вычислительные методы
нений, вычисление определенного интеграла и т.д.). То, что она
принимается за элементарную, предполагает во всяком случае, что ее
выполнение существенно проще вычисления решения всей задачи.
При построении прямых методов существенное внимание уделяется
минимизации числа элементарных операций.
Пример 3.19. (схема Горнера1 ). Пусть задача состоит в вычис­
лении значения многочлена
(3.12)
по заданным коэффициентам а0, а1 , "" ап и значению аргумента х.
Если вычислять многочлен непосредственно по формуле (3.12), причем
х2, х 3, "" xn находить последовательным умножением на х, то потребу­
ется выполнить 2п - 1 операций умножения и п операций сложения.
Значительно более экономичным является метод вычисления, назы­
ваемый схемой Горнера. Он основан на записи многочлена в следую­
щем эквивалентном виде:
Расстановка скобок диктует такой порядок вычислений: S0 = ап, S1 =
=S0x + ап_ 1, S2 = S1x + ап_ 2 , "" S, = S,_ 1x + ап_,, "" Sп = Sп_ 1х + а 0 .
Здесь вычисление значения Рп(х) = Sn потребовало выполнения только
п операций умножения и п операций сложения.
Схема Горнера интересна тем, что дает пример оптимального по
числу элементарных операций метода. В общем случае значение Рп(х)
нельзя получить никаким методом в результате выполнения меньшего
числа операций умножения и сложения. А
Иногда прямые методы называют точными, подразумевая под этим,
что при отсутствии погрешностей во входных данных и при точном
выполнении элементарных операций полученный результат также
будет точным. Однако при реализации метода на компьютере неиз­
бежно появление вычислительной погрешности, которая зависит от
чувствительности метода к погрешностям округления. Многие прямые
(точные) методы, разработанные в домашинный период, оказались
непригодными для машинных вычислений именно из-за чрезмерной
чувствительности к погрешностям округления. Не все точные методы
таковы, однако стоит заметить, что не совсем удачный термин «точ­
ный» характеризует свойства идеальной реализации метода, но отнюдь
не качество полученного при реальных вычислениях результата.
1 Вильяме Джордж Горнер (1786--1837) - английский математик.
65

67. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
4. Итерационные методы. Это - специальные методы построе­
ния последовательных приближений к решению задачи. Применение
метода начинают с выбора одного или нескольких начальных прибли­
жений. Для получения каждого из последующих приближений выпол­
няют однотипный набор действий с использованием найденных ранее
приближений - итерацию'. Неограниченное продолжение этого ите­
рационного процесса теоретически позволяет построить бесконечную
последовательность приближений к решению - итерационную после­
довательность. Если эта последовательность сходится к решению
задачи, то говорят, что итерационный метод сходится. Множество
начальных приближений, для которых метод сходится, называется
областью сходимости метода.
Заметим, что итерационные методы широко используются при
решении самых разнообразных задач с применением компьютеров.
Пр им ер 3.20. Рассмотрим известный итерационный метод, пред­
назначенный для вычисления Ja (где а > О), - метод Ньютона. Зада­
дим произвольное начальное приближение х<0> > О. Следующее при-
ближение вычислим по формуле х<1> = ~ (х<0> + x~oJ, выведенной с
помощью метода линеаризации в примере 3.17 (см. формулу (3.11)).
Продолжив этот процесс далее, получим итерационную последователь­
ность х<0>, x(I>, х<2>, ..., х<п>, ..., в которой очередное (k + 1)-е прибли­
жение вычисляется через k-e по рекуррентной 2 формуле
x<k+ I) = ! (x(k) + ..!!....) k <:: О.
2 x<k) '
(3.13)
Известно, что этот метод сходится при любом начальном приближе­
нии х<0> > О, так что его область сходимости - множество всех поло­
жительных чисел.
Вычислим с его помощью значение J2 на 8-разрядном десятичном
компьютере. Зададим х<0> = 2 (как в примере 3.17). Тогда x(I) = 1.5, х<2> =
= 1.4166667, х<3>= 1.4142157, х<4>= 1.4142136, х!5)= 1.4142136. Дальней­
шие вычисления бессмысленны, так как из-за ограниченности разрядной
сетки все следующие уточнения будут давать тот же результат. Однако
сравнение с точным значением J2 = 1.41421356... показывает, что уже
на третьей итерации были получены шесть верных значащих цифр. А
1От латинского слова 1teratю - «повторение».
2 От латинского слова recurrent - «возвращающийся».
66

68. § 3.3. Вычислительные методы
Обсудим на примере метода Ньютона некоторые типичные для ите­
рационных методов (и не только для них) проблемы. Итерационные
методы по своей сути являются приближенными; ни одно из получае­
мых приближений не является точным значением решения. Однако схо­
дящийся итерационный метод дает принципиальную возможность
найти решение с любой заданной точностью Е > О. Поэтому, применяя
итерационный метод, всегда задают требуемую точность Е и итераци­
онный процесс прерывают, как только она достигается.
Хотя сам факт сходимости метода безусловно важен, он недостаточен
для того, чтобы рекомендовать метод для использования на практике. Если
метод сходится очень меД1Iенно (например, для получения решения
с точностью в 1% нужно сделать 106 итераций), то он непригоден для
вычислений на компьютере. Практическую ценность представляют быстро
сходящиеся методы, к которым относится и метод Ньютона (напомним, что
в рассмотренном выше примере точность Е = 1О-5 в вычислении ,fi бЬUiа
достигнута всего за три итерации). Для теоретического исследования ско­
рости сходимости и условий применимости итерационных методов выводят
так называемые априорные' оцетси погрешности, позволяющие еще до
вычислений дать некоторое заключение о качестве метода.
Приведем две такие априорные оценки для метода Ньютона. Пусть
х<О) > Ja. Известно, что тогда х<п) > Ja для всех ~ ~ О и погрешности
двух последовательных приближений связаны следующим неравенством:
(3.14)
Здесь о<п) = - 1- (х<п> - Ja) = .S(х<п)) - величина, характеризующая
2Ja 2
относительную погрешность п-го приближения. Это неравенство говорит
об очень высокой квадратичной скорости сходимости метода: на каждой
итерации «Ошибка» 5(п) возводится в квадрат. Если выразить в<п) через
погрешность начального приближения, то получим неравенство
(3.15)
из которого видна роль хорошего выбора начального приближения.
Чем меньше о(О) = о(х(О) )/2, тем быстрее будет сходиться метод.
Практическая реализация итерационных методов всегда связана
с необходимостью выбора критерия окончания итерационного про­
цесса. Вычисления не могут продолжаться бесконечно долго и должны
быть прерваны в соответствии с некоторым критерием, связанным,
например с достижением заданной точности. Использование для этой
1 От латинского слова a'priori - «до опыта».
67

69. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
цели априорных оценок чаще всего оказывается невозможным или неэф­
фективным. Качественно верно описывая поведение метода, такие
оценки являются завышенными и дают весьма недостоверную количест­
венную информацию. Нередко априорные оценки содержат неизвестные
величины (например, в оценках (3.14), (3.15) содержится величина Ja),
либо предполагают наличие и серьезное использование некоторой
дополнительной информации о решении. Чаще всего такой информа­
ции нет, а ее получение связано с необходимостью решения дополни­
тельных задач, нередко более сложных, чем исходная.
Для формирования критерия окончания по достижении заданной
точности, как правило, используют так называемые апостериорные 1
оценки погрешности - неравенства, в которых значение погрешности
оценивается через известные или получаемые в ходе вычислительного
процесса величины. Хотя такими оценками нельзя воспользоваться до
начала вычислений, в ходе вычислительного процесса они позволяют
давать конкретную количественную оценку погрешности.
Например, для метода Ньютона (3.13) справедлива следующая апо­
стериорная оценка:
lx(n) - Ja 1~ lx(n) -х<п- l) 1. п ~ 1,
позволяющая оценивать абсолютную погрешность приближения через
модуль разности двух последовательных приближений. Она дает воз­
можность сформулировать при заданной точности Е > О очень простой
критерий окончания. Как только окажется выполненным неравенство
1х(п) - х<п - 1) 1 < Е, (3.16)
вычисления следует прекратить и принять х<п) за приближение к Ja
с точностью 6.
Пр им ер 3.21. Если значение Ji требуется найти с точностью Е =
= 10-5, то неравенство (3.16), как видно из приведенных в примере 3.20
вычислений, будет выполнено при п = 4. Так как ix<4J-x(3Ji = 3 · I0-6,
то с учетом погрешности округления можно записать результат: Ji =
= 1.41421±0.00001 ....
5. Методы статистических испытаний (методы Монте-Карло).
Это - численные методы, основанные на моделировании случайных
величин и построении статистических оценок решений задач. Этот класс
1 От латинского слова a'posteriori - «после опыта».
68

70. § 3.4. Корректность вычислительных алгоритмов
методов, как принято считать, возник в 1949 г., когда Дж. фон Нейман 1
и С. Улам2 использовали случайные числа для моделирования с помо­
щью компьютеров поведения нейтронов в ядерном реакторе. Эти
методы могут оказаться незаменимыми при моделировании больших
систем, но подробное их изложение предполагает существенное
использование аппарата теории вероятностей и математической стати­
стики и выходит за рамки данной книги.
§ 3.4. Корректность вычиспитепьных апгоритмов
1. Вычислительный алrоритм. Вычислительный метод, доведен­
ный до степени детализации, позволяющий реализовать его на компью­
тере, принимает форму вычислительного алгоритма.
Определим вычислительный ш~горитм как точное предписание дей­
ствий над входными данными, задающее вычислительный процесс,
направленный на преобразование произвольных входных данных х (из
множества допустимых для· данного алгоритма входных данных Х)
в полностью определяемый этими входными данными результат.
Реальный вычислительный алгоритм складывается из двух частей:
абстрактного вычислительного ш~горитма, формулируемого в обще­
принятых математических терминах, и программы, записанной на одном
из алгоритмических языков и предназначенной для реализации алго­
ритма на компьютере. Как правило, в руководствах по методам вычисле­
ний излагаются именно абстрактные алгоритмы, но их обсуждение про­
водится так, чтобы выявить особенности алгоритмов, которые оказывают
существенное влияние на качество программной реализации.
2. Определение корректности алrоритма. К вычислительным
алгоритмам, предназначенным для широкого использования, предъяв­
ляется ряд весьма жестких требований. Первое из них - корректность
алгоритма. Будем называть вычислительный алгоритм корректным,
если выполнены три условия:
1) он позволяет после выполнения конечного числа элементарных
для вычислительной машины операций преобразовать любое входное
данное х Е Х в результат у;
1 Джон фон Нейман (1903-1957) - американский математик, физик, инженер-изо­
бретатель. Оказал значительное влияние на развитие современной lатематики. Один из
создателей первых компьютеров. Историческую справку о фон Неймане см. в (54].
2 Станислав Улам (1909-1984)-американский математик. Краткий очерк о ero дея­
тельности можно найти в (54].
69

71. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
2) результат у устойчив по отношению к малым возмущениям вход­
ных данных;
3) результат у обладает вычислительной устойчивостью.
Если хотя бы одно из перечисленных условий не выполнено, то
будем называть алгоритм некорректным. Уточним и более подробно
обсудим эти условия.
Необходимость выполнения первого условия понятна. Если для
получения результата нужно выполнить бесконечное число операций
либо требуются операции, не реализованные на компьютерах, то алго­
ритм следует признать некорректным.
Пр им ер 3.22. Известный алгоритм деления чисел «углом» некор­
ректен, так как он может продолжаться бесконечно, если не опреде­
лен критерий окончания вычислений. А
Пр им ер 3.23. Отсутствие критерия окончания делает некоррект­
ным и алгоритм Ньютона вычисления Fa (см. пример 3.20). А
П р и м ер 3.24. Алгоритм вычисления корней квадратного уравнения
(3.1) по формулам (3.2) некорректен, если он предназначен для использо­
вания на вычислительной машине, на которой не реализована операция
извлечения квадратного корня. А
3. Устойчивость по входным данным. Устойчивость результата у
к малым возмущениям входных данных (устойчивость по входным
данным) означает, что результат непрерывным образом зависит от
входных данных при условии, что отсутствует вычислительная погреш­
ность. Это требование устойчивости аналогично требованию устойчи­
вости вычислительной задачи. Отсутствие такой устойчивости делает
алгоритм непригодным для использования на практике.
Отметим, что в формулировку устойчивости алгоритма по входным
данным неявно входит одно весьма важное предположение, а именно,
что вместе с входным данным х в множество допустимых входных дан­
ных Х входят и все близкие к х приближенные входные данные х•.
Пр им ер 3.25. Пусть алгоритм предназначен для вычисления кор­
ней квадратного уравнения (3.1) с коэффициентами, удовлетворяю­
щими условию d = Ь2 -4с <': О. Если в нем используются формулы (3.2),
то этот алгоритм некорректен. В самом деле, значение d•, отвечающее
приближенно заданным коэффициентам Ь• и с•, может оказаться отри­
цательным, если d"" О. Тогда вычисления завершатся аварийным оста­
новом при попытке извлечь квадратный корень из отрицательного
числа. Если же в формуле (3.2) заменить d на max {d, О}, то алгоритм
становится корректным. А
70

72. § 3.4. Корректность вычислительных алгоритмов
4. Вычислительная устойчивость. Из-за наличия погрешностей
округления при вводе входных данных в компьютер и при выполнении
арифметических операций неизбежно появление вычислительной
погрешности. На разных компьютерах она различна из-за различий в раз­
рядности и способах округления, но для фиксированного алгоритма в
основном значение погрешности определяется машинной точностью Ем.
Назовем алгоритм вычислительно устойчивым, если вычислитель­
ная погрешность результата стремится к нулю при Ем --+ О. Обычно
вычислительный алгоритм называют устойчивым, если он устойчив по
входным данным и вычислительно устойчив, и - неустойчивым, если
хотя бы одно из этих условий не выполнено.
Пр им ер 3.26.1 Пусть требуется составить таблицу значений инте-
1
гралов In = Jxn е 1 -х dx для п = 1, 2, ".на 6-разрядном десятичном ком­
о
пьютере.
Интегрируя по частям, имеем
1 1 1
/п= Jxnd(-e 1 -x)=-xnel-xj~+ Je1-.td(x")=-l+ Jnx11 - 1 e1-xdx.
о о о
Следовательно, справедлива формула
Кроме того,
1
10 = J е 1 -х dx=e-1"'/~=1.71828.
о
(3.17)
Воспользуемся формулой (3.17) для последовательного вычисления
приближенных значений интегралов /п:
11"'/~=11~ -1 = 0.71828;
13 "' 1; = 31; - 1 = о.30968;
15 "'1; = 51;-1 = 0.19360;
17"'!;=11;-1 =0.13120;
19"' 1; = 91;- 1 = -0.55360;
12 "' 1; = 21~ - 1 = 0.43656;
14 "' 1; = 41; - 1 = 0.23872;
16 "'1;=61;-1 =О.16160;
fg "' 1; = 81;- 1 = 0.04960;
/ 10 "' 1~0 = 101;- 1 = -6.5360.
1 Идея примера заимствована нз [5, 106].
71

73. Глава З. Вычислительные задачи, методы и алгоритмы. Основные лонятия
Здесь вычисления следует прекратить. Искомые значения интегралов
очевидно, положительны, а найденные значения при п = 9 и п = 1О
отрицательны. В чем причина появления такой большой погрешности?
В данном примере все вычисления проводились точно, а единствен­
ная и, на первый взгляд, незначительная ошибка была сделана при
округлении значения /0 до шести значащих цифр (заметим, что Л 0 =
= 110 - /~ 1:::: 2 • 10-6). Однако при вычислении /1 эта погрешность
сохранилась, при вычислении /2 умножилась на 2!, при вычислении / 3
- на 3!, .",при вычислении /9 - на 9! и т.д.
Таким образом, Лn = lln - /~ 1 = п!Л 0 • Уже при п = 9 имеем 9! =
= 36 880 и поэтому Л 9 = 9! Л 0 :::: О. 73.
Если вычисления производятся без ограничений на число п, то рас­
сматриваемый алгоритм следует признать вычислительно неустойчи­
вым. Погрешности растут пропорционально п! настолько быстро, что
уже при довольно скромных значениях п попытки добиться приемле­
мого результата даже за счет увеличения разрядности мантиссы зара­
нее обречены на неудачу,
Как изменить алгоритм, чтобы сделать его устойчивым? Перепишем
формулу (3.17) в виде
/ + 1
/ =-п__ n~I
п- 1 п
(3.18)
и будем вести вычисления значений /n в обратном порядке, начиная,
1
например с п = 54. Положим /54 :::: /~ = О. Так как !54 :s; е fх54 dx =
о
= е/55, то Л54 :s; е/55 :::: 5 · 1о-2. Однако при вычислении /53 эта погреш­
ность уменьшится в 54 раза, при вычислении /52 - еще в 53 раза и т.д.
В результате значения In при п = 50, ..., 1 будут вычислены с шестью
верными значащими цифрами. Здесь погрешности не растут, а затухают.
Ясно, что модифицированный алгоритм вычислительно устойчив. .А.
Вычислительная неустойчивость алгоритма часто может быть выяв­
лена благодаря анализу устойчивости по входным данным, так как неус­
тойчивость к малым погрешностям округления входных данных автома­
тически свидетельствует о вычислительной неустойчивости алгоритма.
Пример 3.27. Предположим, что значения Уп для п = 1, 2, ...
вычисляются по рекуррентной формуле
(3.19)
72

74. § 3.5. Чувствительность вычислительных алгоритмов к ошибкам окруmения
а величина у0 задана. Пусть у~ - заданное приближенное значение
величины у0. Тогда (если вычисления ведутся абсолютно точно) опреде­
ляемые по формуле (3.19) приближенные значения содержат погрешно­
сти, связанные равенством Уп - у: = ап(уп _ 1 - у:_,). Следовательно,
л(у:) = 1апl л(у:_ 1) и при выполнении условия lап 1~ l алrоритм устой­
чив по входным данным, поскольку Л(у:) ~ Л(у~) для всех п. Если же
laпl ~ q > l, то л(у:)~qпЛ(у~) и абсолютная погрешность неограни­
ченно возрастает при п --+ оо. В этом случае алrоритм неустойчив по вход­
ным данным, а потому и вычислительно неустойчив. .&
Справедливости ради следует заметить, что алгоритм (3.19) был
признан нами неустойчивым в случае 1а п 1 ~ q > l при выполнении
двух условий, на которых не было достаточно акцентировано внима­
ние. Первое из них состоит в предположении о неограниченной про­
должительности вычислительного процесса (п --+ оо), что невозможно
на практике. В действительности такой характер неустойчивости гово­
рит о тенденции к неограниченному росту погрешности при неограни­
ченном продолжении вычислении. Второе условие касается выбранной
меры погрешности. Совсем не обязательно, чтобы рост абсолютной
погрешности всегда был неприемлем в конкретных вычислениях. Если
он сопровождается сильным ростом точного решения и при этом отно­
сительная погрешность остается малой, то алгоритм можно признать
относительно устойчивым. По-видимому, при анализе вычислительной
устойчивости более естественным является рассмотрение относитель­
ных погрешностей.
Пр им ер 3.28. Пусть в формуле (3.19) все ~п = О и а п * О. Тогда
б(у;) = л(y:)llYпl =1ап1л(у;_,)!lапУп-1I =б(у:_1)· Следовательно,
б(у;) = б(у~) и при любых значениях ап *- О алгоритм относительно
устойчив по ВХОДНЫМ данным....
§ 3.5. Чувствительность вычислительных
алгоритмов к ошибкам округления
Выполнение вычислений на компьютере сопровождается появле­
нием вычислительной погрешности, связанной в первую очередь с необ­
ходимостью округления результата каждой арифметической операции.
Даже если разрядность компьютера велика, существует реальная опас­
ность, что выполнение большого числа операций приведет к накопле­
нию погрешностей, способных значительно или даже полностью иска-
73

75. Глава З. Вычислительные задачи, методы и алгоритмы. Основные понятия
зить вычисляемый результат. Однако и при небольшом числе действий
результат вычислений может оказаться совершенно неправильным,
если алгоритм слишком чувствителен к ошибкам округления.
Начинающий вычислитель часто склонен игнорировать ошибки
округления. На первых порах при решении простых задач, в особенно­
сти если новичок не задумывается о точности найденных решений, его
позицию нетрудно понять. Однако решение серьезных задач (когда
число арифметических операций превышает миллиарды, в вычисления
вкладываются значительные средства, а результат следует получить
с гарантированной точностью и за принятые на основании расчетов
решения приходится нести ответственность) предполагает совсем иное
отношение к вычислительной погрешности.
1. Порядок выполнения операций. Решение математической
задачи на компьютере сводится в конечном итоге к выполнению
последовательности простейших арифметических и логических опера­
ций. Однако часто одно и то же математическое выражение допускает
различные способы вычисления, отличающиеся только порядком
выполнения операций. Если вычисления производить точно, то они
(при любом способе вычисления) будут приводить к одному резуль­
тату. Однако результаты вычислений на компьютере уже зависят от
порядка выполнения операций и различие в вычислительной погреш­
ности может быть весьма значительным.
Рассмотрим простой, но полезный пример вычисления на компью­
N
тере суммы SN = Lа;. Пусть а; - положительные представимые на
i=l
вычислительной машине числа. В каком порядке следует их суммиро­
вать для того, чтобы сделать вычислительную погрешность по возмож­
ности минимальной?
k
Пусть Sk = Lа; - частичная сумма, а s; - ее приближенное зна-
i= I
чение, вычисляемое по формуле s; = s;_1 ® ak. Погрешность значе-
ния s; складывается из погрешности значения s;_ 1 и погрешности
выполнения операции s;_, ® ak. Следовательно, Л(s;) = Л(s;_ 1) +
+ (s;_ 1 + ak)e,..::::: Л(s;_ 1) + Ske,... Поэтому Л(S~) ::::: (SNEм + SN- I е" + .
."+S2e,..)=((N- l)a1 +(N- l)a2 +(N-2)a3 + ." +2aN-l +aN)E,...
Так как множитель, с которым входит а; в формулу для оценки
погрешности, убывает с ростом i, в общем случае погрешность ока-
74

76. § 3.5. Чувствительность вычислительных алгоритмов к ошибкам округления
жется наименьшей, если суммировать числа в порядке возрастания их
значений, начиная с наименьшего.
Иногда неудачно выбранный порядок операций либо приводит к
полной потере точности, либо вообще не дает возможности получить
результат из-за переполнения.
Пр им ер 3.29. Пусть на компьютере типа IBM РС требуется вычис­
лить произведение v = а0 х а1 х а2 х ... х а49 х а50, где а;"' 1025 - i. Если
производить вычисления в естественном порядке, то уже а0 х а1 "' 1044
даст значение, равное +оо. Вычисление произведения в обратном порядке
сразу же приводит к исчезновению порядка, так как а50 х а49 "' 10-49 < Х0 .
В данном случае вполне приемлем следующий порядок операций: v =
= а0 х а50 х а 1 х а49 х ... х а24 х а26 х а25, исключающий возможность
переполнения или антипереполнения. ~
2. Катастрофическая потеря точности. Иногда короткая последо­
вательность вычислений приводит от исходных данных, известных
с высокой точностью, к результату, содержащему недопустимо мало
верных цифр или вообще не имеющему ни одной верной цифры.
В этом случае, как было отмечено в§ 3.2, принято говорить о катастро­
фической потере точности.
Пр и мер 3.301• Известно, что функция ех может быть представлена
в виде сходящегося степенного ряда:
оо xk х2 хз
еХ=""' -=l+x+-+-+
~ k' 2' 31k=O • . •
+~+
п'.
(3.20)
Возможность вычисления значения экспоненты прямым суммиро­
ванием ряда (3.20) кажется привлекательной. Пусть для вычислений
используется 6-разрядный десятичный компьютер. Возьмем х = -8.1
и будем вычислять значения частичных сумм до тех пор, пока добавле­
ние очередного слагаемого еще меняет значение суммы:
е-8.1"' 1.00000 е 8.10000 Е9 32.8050 е 88.5737 Е9 179.362 е 290.566 Е9 ...
••• Е!) 16.4111 87.81941 Е!) ••• =0.000649915.
В сумму вошло 36 слагаемых и значение очередного (37-го) слагае­
мого оказалось уже не в состоянии изменить результат. Можно ли счи­
тать результат удовлетворительным? Сравнение с истинным значением
е-8.1 "' 0.000303539 показывает, что найденное значение не содержит ни
одной верной цифры.
'Идея примера заимствована нз [106].
75

77. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
В чем причина катастрофической потери точности? Дело в том, что
вычисленные слагаемые ряда неизбежно содержат погрешности, причем
для некоторых (для слагаемых с 5-го по 13-е) погрешность превосходит
значение самого искомого результата. Налицо явный дефект алгоритма,
к обсуждению которого мы еще вернемся в конце этого параграфа.
В данном случае переход к вычислениям с удвоенной длиной ман­
тиссы позволит получить значение е-8· 1 с шестью верными значащими
цифрами. Однако всего лишь удвоенное значение аргумента х = -16.2
снова возвращает нас к той же проблеме. Поступим иначе. Используя
разложение (3.20), вычисляем е 8·1 "" 1.00000 вэ 8.1 ООО вэ 32.8050 вэ ... =
=3294.47 и тогда е-8· 1 = l/e8•1 "" 0.000303539. Предложенное изменение
алгоритма позволило получить искомое значение на том же 6-разрядном
десятичном компьютере, но уже с шестью верными значащими цифрами.
Заметим тем не менее, что реальные машинные алгоритмы вычисле­
ния еХ устроены совсем иначе. •
Приведем теперь пример, когда к катастрофической потере точности
приводит еще более короткая последовательность вычислений.
Пр им ер 3.31. Пусть при х = l/490 на 6-разрядном десятичном ком­
пьютере вычисляется значение функции
у= cosx- cos2x. (З.21)
Заметим, что при х"" О величины с1 = cosx"" l -х2/2 и с2 = cos2x""
"" 1- 2х2 близки. Так как вычисленные их приближенные значения с~
и с; будут содержать погрешность, то возможна серьезная потеря точ­
ности. Действительно, с~ = 0.999998, с; = 0.999992 и у• = с~ - с; =
= 0.000006. При вычитании старшие разряды оказались потерянными
и в результате осталась только одна значащая цифра.
Вычисление по эквивалентной формуле у = 2 sin(x/2) sin(3x/2),
позволяет избежать вычитания близких чисел и дает значение у* =
= 0.624741·10-5 с шестью верными цифрами.
Интересно отметить, что у "" 1.5х2, причем использование этой при­
ближенной формулы в данном случае дает шесть верных значащих
цифр, в то время как вычисления по формуле (З .21) - только одну
верную цифру. 6.
76
Зам е чан и е. Не всегда катастрофическая потеря точности
в промежуточных вычислениях действительно является катастро­
фой. Все зависит от того, как в дальнейшем используется результат.

78. § 3.5. Чувствительность вычислительных алгоритмов к ошибкам округления
3. Обусловленность вычислительного алгоритма. По аналогии
с понятием обусловленности математической задачи можно ввести
понятие обусловленности вычислительного алгоритма, отражающее
чувствительность результата работы алгоритма к малым, но неизбеж­
ным погрешностям округления. Вычислительно устойчивый алгоритм
называют хорошо обусловленным, если малые относительные погреш­
ности округления (характеризуемые числом Ем) приводят к малой
относительной вычислительной погрешности () (у0 ) результата у•, и
плохо обусловленным, если вычислительная погрешность может быть
недопустимо большой.
Если о(у*) и Ем связаны неравенством о(у0 ) ~ vА Е", то число vА сле­
дует называть числом обусловленности вычислительного алгоритма.
Для плохо обусловленного алгоритма vА » 1.
При очень большом значении числа обусловленности алгоритм
можно считать практически неустойчивым 1•
Применим, например алгоритм, первоначально предложенный в при­
мере 3.26, для вычисления конечной серии из N интегралов /1, / 2, ... , IN.
Тогда коэффициент роста погрешности vА окажется конечным. Иными
словами, при вычислении конечной серии интегралов алгоритм фор­
мально оказывается устойчивым. Тем не менее уже при не очень боль­
ших значениях N он настолько плохо обусловлен, что в практическом
плане может считаться неустойчивым.
Для решения хорошо обусловленной задачи нет смысла применять
плохо обусловленный алгоритм. Именно такими являются алгоритмы,
первоначально предложенные в примерах 3.26 и 3.30.
Вернемся к примеру 3.30. Задача вычисления функции ех хорошо
обусловлена (см. пример 3.10). Можно ли было предвидеть катастрофи­
ческую потерю точности при вычислении значения е-8· 1 прямым сум­
мированием ряда (3.20)?
00
Рассмотрим задачу суммирования ряда L ak со слагаемыми ak =
k=O
xk
= k! . Каждое из этих слагаемых вычисляется с относительной
погрешностью <>(а;) ~ Е". При х <О формула (3.10) с учетом разло-
оо 1 lk 00 k
жения (3.20) дает значение v13 = L ~! / / L ~ /= e21:rl. Рост модулях
k=O k=O
1 Иногда такие плохо обусловленные алгоритмы называют численно неустойчивыми.
п

79. Глава З. Вычислительные задачи, методы и алгоритмы. Основные понятия
(для х < О) приводит к резкому ухудшению обусловленности вычисле­
ний. Для х =-8.1, как в примере 3.30, имеем v15 =е 1 6 2 ~ 107• Поэтому
неудивительна полная потеря точности при вычислениях на 6-разряд­
ном десятичном компьютере.
Рассмотрим теперь обусловленность алгоритма прямого вычисления
по формуле (3.21 ). При малых х вычисленные приближения с~ ~ cos х
и с;~ cos 2х содержат погрешности порядка Ем. Поэтому Л(у*} - 2Ем.
Учитывая, что у ~ 1.5х2 , находим оценку границы относительной
погрешности б (у*} - х-1 Ем. Число обусловленности v - х-1 быстро
растет с уменьшением 1х1. Уже при 1х1 .$ F,. эта оценка дает
б(у*) >> 1, т.е. говорит о катострофической потере точности.
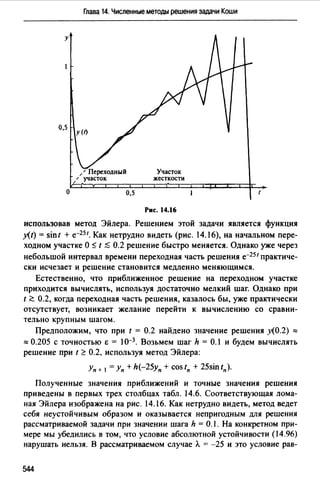
Если алгоритм, предназначенный для решения хорошо обусловленной
задачи, оказался плохо обусловленным, то его следует признать неудов­
летворительным и попытаться построить более качественный алгоритм.
В примерах 3.30 и 3.31 это удалось сделать сравнительно легко.
Однако для плохо обусловленных задач дело обстоит иначе. Ключ
к пониманию дает следующее высказывание [81]: «Если задача плохо
обусловлена, то никакие усилия, потраченные на организацию изо­
щренных вычислений, не могут дать правильных ответов, исключая
случайности». Здесь требуется серьезное переосмысление постановки
вычислительной задачи.
§ 3.6. Различные подходы к анализу оwибок
1. Прямой анализ ошибок. Общий эффект влияния ошибок обычно
учитывают следующим образом. Изучают воздействие ошибок выходных
данных, метода и округлений на получаемый результат у• и пытаются
оценить некоторую меру близости у• к истинному решению у. Такой
метод исследования называют прямым анализом ошибок. В большинстве
случаев в данной книге мы будем следовать этому традиционному пути.
Во многих (но далеко не во всех) случаях оценки погрешности удается
получить; однако довольно часто они оказываются сильно завышенными
и приводят к неоправданному пессимизму в оценке качества приближен­
ного решения. Реальное значение погрешности у - у• часто значительно
меньше, чем ее оценка, рассчитанная на самый неблагоприятный случай
и выведенная с помощью прямого анализа. Особенно трудным является
прямой анализ вычислительной погрешности.
78

80. § 3.6. Различные подходы к анализу ошибок
2. Обратный анализ ошибок. В последнее время получил широкое
распространение другой подход к оценке влияния ошибок. Оказыва­
ется, что довольно часто приближенное решение у• можно трактовать
как точное решение той же задачи, но отвечающее возмущенным вход­
ным данным х·. Оценка такого эквивалентного возмущения входных
данных и является целью обратного анализа ошибок.
В прикладных задачах входные данные, как правило содержат
погрешности. Обратный анализ показывает, что ошибки, внесенные в
решение в процессе его вычисления, оказываются равносильными неко­
торым дополнительным ошибкам внесенным во входные данные. Сопос­
тавление величины этого эквивалентного возмущения и уровня ошибок
входных данных позволяет судить о качестве найденного решения. На
рис. 3.5 представлена графическая иллюстрация обратного анализа оши­
бок. Здесь данное х• таково, что решением задачи, соответствующим х•,
является у• - результат приближенного решения задачи с входным дан­
ным х. На рисунке заштрихована область неопределенности входного
данного; в пределах этой области входные данные для решающего задачу
неразличимы. В представленном случае х· оказалось внутри этой
области, поэтому результат у• следует признать вполне приемлемым.
Каждый из указанных двух подходов к оценке погрешности имеет
свои достоинства и полезным является разумное их сочетание.
Пр им ер 3.32. Пусть на 6-разрядном десятичном компьютера
вычисляется корень уравнения
х5 - 12.5х4 + 62.5хз - 156.25х2 + 195.3125х - 97.65625 =О.
При вводе в компьютер последние два коэффициента будут округлены
до шести значащих цифр и уравнение примет вид:
Р0(х) = х5 - 12.5х4 + 62.5хз - 156.25х2 + I95.3 I3x - 97.6563 = О. (3.22)
Область неопределенности
входного данного
Рис. 3.S
Область неопределенности
решения
79

81. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
Допустим, что некоторый алгоритм, примененный к этому уравне­
нию, дал значение приближенного решения х* = 2.6. Следуя логике пря­
мого анализа ошибок, чтобы оценить качество полученного приближения
нужно было бы задаться вопросом: насколько отличается х* от истинного
решения х уравнения (3.22)? Мы поступим иначе. Подставляя х* в левую
часть уравнения (3.22), получаем значение Р*(х*) = 0.00126. Заметим
теперь, что х* = 2.6 является точным решением уравнений
х5 - 12.5х4 + 62.5хз - 156.25х2 + 195.3125х - 97.65626 =О;
х5 - 12.5х4 + 62.5хз - 156.25х2 + 195.31252х - 97.656312 =О,
которые после округления коэффициентов до шести значащих цифр
совпадают с уравнением (3.22) и становятся неотличимы от исходного
уравнения. Найденное решение следует признать превосходным с
точки зрения «философию> обратного анализа ошибок, так как оно явля­
ется точным решением задачи, лежащей в пределах области неопреде­
ленности задачи (3.22). Рассчитывать на то, что после записи уравнения в
виде (3.22) удастся получить лучший ответ, просто бессмысленно.
Конечно, это немного обидно, особенно если учесть, что исходное уравне­
ние в действительности есть развернутая запись уравнения (х - 2.5)5 = О
и истинным значением корня является х = 2.5. А
Представляется, что значение обратного анализа ошибок недоста­
точно осознанно, в особенности среди непрофессиональных вычисли­
телей. Этот подход показывает на возможность иного взгляда на оценку
качества приближенного решения, а значит, и на качество многих
вычислительных алгоритмов. Сложившийся стереотип заставляет искать
приближенное решение у* математической задачи, мало отличающееся
от ее истинного решения у. Однако для большинства практических
задач в силу неопределенности в постановке и входных данных в дей­
ствительности существует и область неопределенности решения
(рис. 3.5). Поскольку эта область неизвестна, оценить степень близости
вычисленного решения у* к ней очень трудно. Гораздо проще, быть
может, получить ответ на аналогичный вопрос для входного данного х*,
соответствующего решению у*. Поэтому можно сформулировать цель
вычислений и так: «найти точное решение задачи, которая мало отли­
чается от поставленной задачи» или же так: «найти решение задачи
с входным данным х*, находящимся в пределах области неопределенно­
сти заданного входного данного х».
Пр и мер 3.33. Пусть для задачи Коши
у' - JY = а(х)х, у(1) = 2, (3.23)

82. § 3.6. Различные подходы к анализу ошибок
где а(х) = 2.6 + 0.01 е--х, найдено приближенное решение у = 2х2. Как
оценить его качество?
Условие y(l) = 2, очевидно, выполнено. Подставляя у(х) в левую
часть уравнения, убеждаемся, что у(х) удовлетворяет уравнению (3.23)
с коэффициентом а• = 4 - J2 ::::: 2.586 вместо а. Обратим внимание на
то, что «истинное» значение а 0 коэффициента а нам в действительно­
сти неизвестно и а(х) - лишь некоторое его приближение. Числовой
параметр 2.6 в лучшем случае получен округлением «истинного» зна­
чения, и, следовательно, а может отличаться от а 0 и на 0.05. Так как
1а• - а 1 :-::; 0.03, то в силу естественной неопределенности в постановке
задачи функция у = 2х 2 с позиции обратного анализа ошибок может
считаться таким же равноправным решением поставленной задачи, как
и найденное сколь угодно точно решение задачи (3.23). Во всяком слу­
чае теперь для того, чтобы отказаться от найденного приближенного
решения, нужны довольно веские аргументы. .А.
Подчеркнем, что в основе методов решения некорректных и плохо
обусловленных задач также лежит существенное переосмысление
постановок вычислительных задач.
3. Статистический анализ ошибок. Даже для простых алгоритмов
строгий анализ влияния ошибок округления очень сложен. При боль­
шом числе выполняемых операций гарантированные оценки погрешно­
сти, рассчитанные на самый неблагоприятный случай, как правило,
бывают сильно завышенными.
Можно надеяться на то, что появляющиеся в реальном вычислитель­
ном процессе ошибки округления случайны и их взаимное влияние
приводит к определенной компенсации результирующей ошибки. Ста­
тистический анализ ошибок исходящий из предположения об их слу­
чайности, направлен на исследование не максимально возможных,
а наиболее вероятных ошибок.
Для сравнения покажем отличие в результатах на примере задачи
N
вычисления суммы SN = Lak большого числа положительных слагае-
k~1
мых. Гарантированная оценка погрешности дает значение относитель-
ной погрешности o(S~), растущее пропорционально N. 8 ТО же время
статистический анализ показывает, что если ошибки округления явля­
ются случайными с нулевым средним значением, то o(S~) растет про-
порционально JN, т.е. гораздо медленнее. К сожалению, на тех компь-
81

83. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
ютерах, где округление производится усечением, последнее
предположение не выполнено, так как ошибки округления смещены в
одну сторону и поэтому имеют ненулевое среднее значение. Здесь
o(S,~) растет опять пропорционально N.
4. Некоторые нестрогие способы анализа. Распространенным
методом оценки влияния вычислительной погрешности является расчет
с обычной и удвоенной точностью. Если результаты двух вычислений
получаются существенно различными, это является свидетельством
плохой обусловленности алгоритма. В то же время есть надежда на то,
что совпадающие в ответах цифры верны.
Примерно такие же суждения о чувствительности решения к ошибкам
округления можно сделать, если провести вычисления на двух различных
вычислительных машинах или использовать различные компиляторы.
Разумеется, такое исследование имеет смысл провести на одном-двух
типичных примерах до начала массовых однотипных расчетов.
Влияние ошибок во входных данных на результат вычислений
можно увидеть, если решить задачу несколько раз, изменив случайным
образом входные данные в пределах ошибки их задания. Проделав
такой эксперимент несколько раз, можно грубо оценить погрешность
решения, вызванную погрешностями входных данных.
§ 3.7. Требования, предъявляемые
к вычислительным алгоритмам
В § 3.4 и 3.5 были сформулированы два важнейших требования -
корректность и хорошая обусловленность. Кроме них, к алгоритмам
предъявляется еще целый ряд существенных требований.
1. Требования к абстрактным алгоритмам. К числу этих требо­
ваний относятся: экономичность, надлежащая точность, экономия
памяти, простота.
Экономичность алгоритма измеряется числом элементарных опера­
ций, необходимых для его реализации, и в конечном итоге сводится
к затратам машинного времени. Это требование формулируют иногда
как требование максимальной быстроты исполнения алгоритма. Эконо­
мичность особенно важна при массовых расчетах. Естественно, что
при создании алгоритмов большое внимание уделяют минимизации
числа операций Для некоторых задач разработаны алгоритмы, требую­
щие минимально возможного числа операций. Пример такого алго-
82

84. § 3.7. Требования, предъявляемые к вычислительным алгоритмам
ритма - схема Горнера (см. пример 3.19). Отметим, что ряд математи­
ческих алгоритмов, созданных в домашинный период, оказался
удивительно неэкономичным. Приведем классический пример такого
алгоритма.
Пример 3.34 (правило Крамера 1 ). Для решения системы
линейных алгебраических уравнений Ах = Ь порядка т по правилу Кра­
мера предлагается вычислять компоненты вектора х как отношения спе­
циальным образом построенных определителей: х1=Л1/ Л, i = l, 2, .", т.
Если вычислять определитель непосредственно по его определению, то
нужно выполнить (m - 1)m! умножений и m! сложений. Пусть для вычис­
лений используется компьютер с производительностью 106 умножений в
секунду и решается система с числом неизвестных т = 15, весьма
скромным для приложений. Тогда вычисление только одного определи­
теля потребует 14 · 15! "" 1.8 · 1013 умножений, в результате чего на
вычисление решения уйдет около lО лет непрерывной работы компью­
тера. Вместе с тем для решения той же системы на том же компьютере
методом Гаусса (см. гл. 5) потребуется примерно 0.002 с. Естественно, что
как вычислительный алгоритм правило Крамера следует забраковать. _.
Даже для самых простых задач выбор экономичного алгоритма
может дать существенное уменьшение числа операций.
Пр им ер 3.35. Пусть требуется вычислить хп, где п - натуральное
число. Вычисление этой величины последовательным умножением на х
предполагает выполнение п - 1 операций умножения. Нетрудно убе­
диться в том, что этот способ не самый экономичный. Например, х64
можно найти, выполнив не 63, а всего шесть операций умножения, если
последовательным возведением в квадрат вычислить х2, х4, х8, х16, х32, х64.
В общем случае представим п в виде разложения (2.25) по степеням
числа 2 (именно так число п хранится в памяти компьютера). Тогда
La L-ICJ.L 2 а а
Хп = (х2 ) L • (х2 ) - 1 • (Х ) 1 • Х О. (3.24)
Заметим, что в произведении (3.24) следует учитывать при вычисле­
нии только те сомножители, для которых а1 '#О (т.е. а;= l). Алгоритм,
1 Габриэль Крамер (17~1752) - швейцарский математик.
83

85. Глава З. Вычислительные задачи, методы и алгоритмы. Основные понятия
основанный на разложении (3.24), называется бинарным алгоритмом.
Он позволяет найти xn не более чем за 2 log 2п операций умножения. .А.
3 а меч ан и е. Традиционно временные затраты на выполнение
алгоритма оцениваются числом выполняемых им операций с пла­
вающей точкой (флопов). Нужно иметь в виду, что на современ­
ных компьютерах такие оценки не вполне корректны, поскольку
игнорируют временные затраты на передачу данных. В первую
очередь это относится к параллельным компьютерам, но верно
также и для рабочих станций и персональных компьютеров. Вре­
менные затраты на пересылку данных в персональных компьюте­
рах могут превысить время на выполнение арифметических опе­
раций.
Требование точности означает, что вычислительный алгоритм
должен давать решение задачи с заданной или приемлемой для
задачи ТОЧНОСТЬЮ Е.
Важным является требование экономии памяти. Хотя в последнее
время доступная память компьютеров существенно расширилась, для
«больших)) задач требование экономии памяти может в ряде случаев
стать основным. Интерес к экономному размещению информации
в памяти возрастает в связи со все более широким использованием
персональных компьютеров для решения научно-технических и
инженерных задач.
Учитывая необходимость дальнейшей программной реализации
алгоритма, подчеркнем, что простота алгоритма также является
весьма желательным его свойством.
2. Требования к программным реализациям алгоритмов. К
настоящему времени выработан ряд требований к программам, реали­
зующим вычислительные алгоритмы и предназначенным для длитель­
ного и широкого использования. Перечислим некоторые из них:
надежность, работоспособность (робастность), переносимость (порта­
бельность), поддерживаемость, простота в использовании и др. Рас­
смотрим эти требования более подробно.
Надежность программы означает, что она не содержит ошибок
и вычисляет именно тот результат, для которого она предназначена.
Работоспособность (робастность) включает в себя надежность
и предполагает, что программа способна выявлять недопустимые исходные
данные, обнаруживать различные критические для задачи или алгоритма
ситуации. Робастная программа реагирует на такие ситуации приемлемым
для пользователя образом. Она составлена так, чтобы исключить недо-
84

86. § 3.7. Требования, предъявляемые к вычислительным алгоритмам
пустимые операции типа деления на нуль и попытки извлечь квадратный
корень или вычислить логарифм от отрицательного числа.
Алгоритм может <шотерпеть неудачу» при решении задачи, если
заданное входное данное не является для него допустимым. Конечно,
в простых ситуациях пользователь должен сам различать допустимые
для алгоритма входные данные от недопустимых. Однако чаще всего
сделать это до вычисдений очень трудно или невозможно, и в про­
грамме должен быть предусмотрен анализ данных и сообщение пользо­
вателю о недопустимых или сомнительных данных. Необходимо
исключить ситуацию, характерную для некачественных программ,
когда реакцией на задание данных, при которых алгоритм не может по
объективным причинам найти решение Jадачи, является прекращение
работы программы без сообщения причины останова, или же выдача
внешне вполне правдоподобного, но совершенно бессмысленного
результата.
Переносимость (портабельность) означает, что программа может
работать на различных компьютерах без изменения или с незначитель­
ными изменениями. Всякая характеристика компьютера, используемая
в программе (например, значение машинного эпсилон Ем), должна или
вычисляться самой программой, или задаваться пользователем.
1
Замечание. Принятие IEEE стандарта значительно упростило
решение проблемы переносимости.
Поддерживаемость означает прежде всего требование легкости
модификации. Для того чтобы была возможность внесения в про­
грамму изменений с минимальной вероятностью появления ошибок,
она должна быть составлена максимально ясно и логично. Полезно
вносить в текст программы содержательные комментарии. Разобраться
в плохо составленной программе может оказаться труднее, чем создать
новую. Поддерживаемая программа должна быть хорошо документиро­
вана. Плохое описание программы в лучшем случае способно вызвать к
ней недоверие, а в худшем - может не позволить пользователю пра­
вильно ее эксплуатировать. К сожалению, нередка ситуация, когда
предназначенная для широкого использования программа настолько
плохо документирована, что пользователь предпочитает потратить
время на написание аналогичной программы (возможно, гораздо худ­
шего качества) либо вообще отказаться от решения задачи.
Простота в использовании программы - весьма желательное, но
трудно достижимое свойство. Часто добиться простоты в использова­
нии можно только жертвуя надежностью или экономичностью. Сущест­
вует ряд широко используемых программ, которые, в первую очередь,
популярны, благодаря простоте в использовании.
85

87. Глава 3. Вычислительные задачи, методы и алгоритмы. Основные понятия
3. Противоречивость требований. Можно продолжить перечисле­
ние требований к вычислительным алгоритмам, добавив, например
требования универсальности и гибкости. Однако нетрудно понять, что
сформулированные требования противоречивы. Большинство из них
вступает в противоречие с экономичностью, выраженной через затраты
машинного времени. В разных ситуациях на первый план может высту­
пать то или иное требование и, удовлетворяя в большей степени одним
требованиям, программа с неизбежностью в меньшей степени удовле­
творяет другим. Это частично объясняет наличие большого числа про­
грамм, предназначенных для решения одной и той же задачи.
Естественно, что хорошая программа, которую можно предъявить
для широкого использования, не может быть простой. Следует при­
знать, что составление таких программ - это работа, требующая высо­
кой квалификации и специальных знаний. Ее выполняют специалисты
по созданию математического обеспечения компьютеров. Рядовой
пользователь должен по возможности стремиться максимально исполь­
зовать стандартные программы, а не создавать новые.
§ 3.8. Допопнитепьные замечаниw
Учебные пособия [97, 37] можно рассматривать как введение в тео­
рию методов решения некорректных задач. Их удачно дополняют сле­
дующие книги [7, 72, 98]. Отметим, что [98] содержит не только теорию
и алгоритмы, но и тексты соответствующих программ.
2 Весьма содержательное изложение проблемы обусловленности
вычислительных задач и обратного анализа ошибок содержится в (81).
Здесь же подробно обсуждаются проблема создания высококачествен­
ного математического обеспечения и требования, предъявляемые к
вычислительным алгоритмам.
86

88. Глава 4
МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе рассматривается задача отыскания корней нелинейных
уравнений и излагаются методы ее решения. Это делается несколько
подробнее, чем обычно принято в учебниках по численным методам.
Дело в том, что нелинейное уравнение представляет собой редкий при­
мер задачи, которая может быть сравнительно полно исследована эле­
ментарными средствами и допускает наглядные геометрические иллю­
страции. В то же время многие проблемы, возникающие при отыскании
корней нелинейных уравнений, типичны, а некоторые методы их реше­
ния (в особенности метод простой итерации и метод Ньютона) допус­
кают широкие обобщения и играют в вычислительной математике фун­
даментальную роль.
§ 4.1. Постановка задачи. Основные этапы решения
1. Постановка задачи. Задача отыскания корней нелинейного урав­
нения с одним неизвестным вида
f(x) =О (4.1)
имеет многовековую историю, но не потеряла свою актуальность и в
наши дни. Она часто возникает как элементарный шаг при решении раз­
личных научных и технических проблем. Напомним, что корнем (или
решением) уравнения (4.1) называется значение х, при которомf(х) =О.
Для справедливости большинства рассуждений данной главы доста­
точно предположить, что в окрестности каждого из искомых корней
функция f(x) дважды непрерывно дифференцируема.
Корень х уравнения (4.1) называется простым, если f'(x) * О.
В противном случае (т.е. в случае f'(x) = О) корень х называется
кратным. Натуральное число т назовем кратностью корня х, если
j(k)( х )= О для k = 1, 2, ... , т - 1 и j(m)( х )*О. Геометрически корень х
соответствует точке пересечения графика функции у= f(x) с осью Ох.
Корень х является простым, если график пересекает ось Ох под нену­
левым углом, и кратным, если пересечение происходит под нулевым
87

89. Глава 4. Методы отыскания решений нелинейных уравнений
у
х
Рис. 4.1
углом. Функция f(x), график который изображен на рис. 4.1, имеет
четыре корня. Корни х 1 и х3 - простые, х2 и х4 - кратные.
Задача отыскания простых корней является существенно более
простой (и чаще встречающейся), чем задача отыскания кратных кор­
ней В действительности большинство методов решения уравнения
(4.1) ориентировано именно на вычисление простых корней.
2. Уточнение постановки задачи. В конкретной задаче часто инте­
рес представляют не все корни уравнения, а лишь некотор1;.1е из них.
Тогда постановку задачи уточняют, указывая на то, какие из корней
подлежат определению (положительные корни, корни из заданного
интервала, максимальный из корней и т.д.).
В подавляющем большинстве случаев представить решение уравне­
ния (4.) в виде конечной формулы оказывается невозможным. Даже
для простейшего алгебраического уравнения п-й степени
(4.2)
явные формулы, выражающие его корни через коэффициенты с помо­
щью конечного числа арифметических операций и операций извлече­
ния корней степени не выше п, найдены 1 лишь при п = 2, 3, 4. Однако
уже для уравнений пятой и более высоких степеней таких формул не
существует. Этот замечательный факт, известный как теорема Абеля,
был установлен в 30-е годы XIX в. Н. Абелем 2 и Э. Галуа 3.
1 Алгебраические уравнения третьей и четвертой степеней не поддавались усилиям
математиков около 2000 лет. Эту задачу решили итальянские математики эпохи Ренес­
санса Сципион дель Ферро (1456-1526), Никколо Тарталья (1500--1557), Джироламо
Кардано (1501-1576), Людовико Феррари (1522-1565).
2 Нильс Хенрик Абель (1802-1829) - норвежский математик. Теорема, о которой
идет речь, была доказана им в возрасте около 22 лет.
3 Эварист Га ~уа (1811-1832) - французский математик, один из создателей теории
групп. Убит на дуэли в возрасте 21 года. Краткий очерк о его жизни см. в [54].
88

90. § 4.1. Постановка задачи. Основные этапы решения
Невозможность найти точное решение нелинейного уравнения
кажется огорчительной. Однако нужно признать, что желание найти
точное числовое значение решения вряд ли следует считать разумным.
Во-первых, в реальных исследованиях зависимость у = f(x) является
лишь приближенным описанием, моделирующим истинную связь
между параметрами у и х. Поэтому точное решение х уравнения (4.1)
все равно является лишь приближенным значением того параметра х,
который в действительности соответствует значению у = О. Во-вторых,
даже если уравнение (4.1) допускает возможность нахождения решения
в виде конечной формулы, то результат вычислений по этой формуле
почти с неизбежностью содержит вычислительную погрешность и
поэтому является приближенным.
Пример 4.1. Предположим, что исследование некоторого явления
привело к необходимости решить уравнение
х 2 - 3.3х + 2.7 =О. (4.3)
Воспользовавшись формулами (3.2) для корней квадратного уравне­
ния, получим значения х 1 = 1.5, х 2 = 1.8. Найдены ли нами точные
значения параметра х? Очевидно, нет. Скорее всего коэффициенты
уравнения (4.3) известны приближенно и в лучшем случае они пред­
ставляют округленные значения «истинных» коэффициентов. В дейст­
вительности можно лишь утверждать, что х 1 ::::: 1.5, х 2 ::::: 1.8.
Предположим теперь, что «истинный» вид уравнения (4.3) таков:
х 2 - 3.3287х + + 2.6631 = О. Тогда точные значения параметра можно
вычислить по формуле х1 2 = (3.3287 ± J3.32872 - 4 · 2.6631 )/2. Однако
она лишь указывает на то, какие операции и в каком порядке следует
выполнить В данном случае точное вычисление по формуле невоз­
можно, так как она содержит операцию извлечения квадратного корня.
Вычисленные по ней значения х 1 , х 2 неизбежно окажутся приближен­
ными....
В дальнейшем мы откажемся от попыток найти точные значения
корней уравнения (4.1) и сосредоточим внимание на методах решения
более реалистичной задачи приближенного вычисления корней с задан­
ной ТОЧНОСТЬЮ Е.
3. Основные этапы решения. Решение задачи отыскания корней
нелинейного уравнения осуществляют в два этапа Первый этап назы­
вается этапом локализации (или отделения) корней, второй - этапом
итерационного уточнения корней.
89

91. Глава 4. Методы отыскания решений нелинейных уравнений
Локализация корней. Отрезок [а, Ь], содержащий только один
корень х уравнения (4.1 ), называют отрезко.u локализации корня х.
Цель этапа локализации считают достигнутой, если для каждого из
подлежащих определению корней удалось указать отрезок локализации
(его длину стараются по возможности сделать минимальной).
Прежде чем переходить непосредственно к отысканию отрезков
локализации, имеет смысл провести предварительное исследование
задачи для выяснения того, существуют ли вообще корни уравнения
(4.1 ), сколько их и как они расположены на числовой оси.
Способы локализации корней многообразны, и указать универсаль­
ный метод не представляется возможным. Иногда отрезок локализации
известен либо он определяется из физических соображений. В простых
ситуациях хороший результат может давать графический метод (см. при­
мер 4.2). Широко применяют построение таблиц значений функций f
вида У;= f(x; ), i = 1, 2, ..., п. При этом способе локализации о наличии на
отрезке [х; _1, х;] корня судят по перемене знака функции на концах
отрезка (см. пример 4.3). Основанием для применения указанного спо­
соба служит следующая хорошо известная теорема математического ана­
лиза.
Теорема 4.1. Пусть функция/непрерывна на отрезке [а, Ь] и при­
нимает на его концах значения разных знаков, т.е. f(a) · f(b) < О. Тогда
отрезок [а, Ь] содер:ж:ит по крайней мере один корень уравнения f(x) =О. •
К сожалению, корень четной кратности не удается локализовать на
основании перемены знака с помощью даже очень подробной таблицы.
Дело в том, что в малой окрестности такого корня (например, корня х 2
на рис. 4.1) функция f имеет постоянный знак.
Важно подчеркнуть, что далеко не всегда для успешного отыскания
корня х уравнения (4.1) необходимо полное решение задачи локализа­
ции. Часто вместо отрезка локализации достаточно найти хорошее
начальное приближение х<О) к корню х .
Пр им ер 4.2. Локализуем корни уравнения
4(1-х 2 )-ех=о. (4.4)
Для этого преобразуем уравнение к виду 1 - х2 = 0.25 ех и построим
графики функций у = 1 - х2 и у = 0.25 еХ (рис. 4.2). Абсциссы точек
пересечения этих графиков являются корнями данного уравнения. Из
рис. 4.2 видно, что уравнение имее'f два корня х 1 и х2 , расположенные
на отрезках [-1, О] и [О, 1]. Убедимся, что функция f(x) = 4(1 - х2)- ех
90

92. § 4.1. Постановка задачи. Основные этапы решения
у
х
Рис. 4.2
принимает на концах указанных отрезков значения разных знаков. Дей­
ствительно, /(-1) = -е-1 <О, /(О)= 3 >О, /(1) =-е <О.
Следовательно, в силу теоремы 4.1 на каждом из отрезков [-1, О]
и [О, 1] находится по крайней мере один корень. •
Пр им ер 4.3. Локализуем корни уравнения
хз - l.lx2- 2.2х + 1.8 =О.
Для этого составим таблицу значений функции f(x) = хз - l. Jx2 -
- 2.2х + 1.8 на отрезке [-2, 2] с шагом 0.4 (табл. 4.1 ).
Таблица 4.1
х -2.0 -1.6 -1.2 -{),8 -{).4 О.О
f(x) -6.200 -1.592 1.128 2.344 2.440 1.800
Продолжение табл. 4. 1
х 0.4 0.8 1.2 1.6 2.0
f(x) 0.808 -0.152 -0.696 -0.440 1.000
Из таблицы видно, что функция f меняет знак на концах отрезков
[-1.6, -1.2], [0.4, 0.8], [1.6, 2.0]. Теорема 4.1 дает основание утверждать,
что каждый из этих отрезков содержит по крайней мере один корень.
Учитывая, что в силу основной теоремы алгебры многочлен третьей
степени не может иметь более трех корней, заключаем, что полученные
три отрезка содержат ровно по одному корню. Таким образом, корни
локализованы. •
Итерационное уточнение корней. На этом этапе для вычис­
ления каждого из корней с точностью Е > О используют тот или иной
итерационный метод, позволяющий построить последовательность
х<0>, хО>, "., х<11>, ".приближений к корню х.
91

93. Глава 4. Методы отыскания решений нелинейных уравнений
Общее представление об итерационных методах и основные опреде­
ления были даны в § 3.3. Введем дополнительно некоторые определения.
Итерационный метод называют одношаговым, если для вычисления
очередного приближения х<п + 1) используется только одно предыдущее
приближение х<п> и k-шаговым, если для вычисления х<п + l) использу­
ются k предыдущих приближений х<п -k + 1>, х<п-k + 2>, ...,х<п>. Заметим,
что для построения итерационной последовательности одношаговым
методом требуется задание только одного начального приближения х<0>,
в то время как при использовании k-шагового метода - k начальных
приближений х<0>, x(IJ, "., x<k- 1).
Скорость сходимости - одна из важнейших характеристик итера­
ционных методов. Говорят, что метод сходится со скоростью геомет­
рической прогрессии, знаменатель которой О < q < 1, если для всех п
справедлива следующая оценка:
lx(n) - х 1 ~ c0qn. (4.5)
Как нетрудно видеть, из оценки (4.5) действительно вытекает сходи­
мость метода.
Пусть одношаговый итерационный метод обладает следующим
свойством: существует а-окрестность корня х такая, что если прибли­
жение х<п> принадлежит этой окрестности, то справедлива оценка
iх<п + l) - Х 1 ~ Clx(n) _ Х IP, (4.6)
где С > О и р ~ 1 - постоянные. В этом случае число р называют поряд­
ком сходимости метода. Если р = 1 и С < 1, то говорят, что метод обла­
дает линейной скоростью сходимости в указанной а-окрестности корня.
Если р > 1, то принято говорить о сверх.линейной скорости сходимости.
При р = 2 скорость сходимости называют квадратичной, а при р = 3 -
кубической. При наличии оценки (4.6) у k-шагового метода (при k > 1)
число р также будем называть порядком сходимости метода.
Лемма 4.1. Пусть одношаговый итерационный метод обладает
линейной скоростью сходимости в некоторой а-окрестности корня х .
Тогда при любом выборе начального прибли:жения xlO) из а-окрестно­
сти корня х итерационная последовательность х<п) не выходит за
пределы этой окрестности, метод сходится со скоростью геометри­
ческой прогрессии со знаменателем q = С < 1 и имеет место следую­
щая оценка погрешности:
lх<п) - Х 1~ qnlx(O)_ Х I, п ~О. (4.7)
До к аз ат ель ст в о. Заметим, что принадлежность х<п> окрестности
(х - а, х - а) является следствием неравенства (4.7). В самом деле,
92

94. § 4.2. Обусловленность задачи вычисления корня
так как q < 1, то 1х<п) - х 1:S 1х<0> - х 1< а. Сходимость х<п> к х также
вытекает из (4.7).
Справедливость неравенства (4.7) установим методом индукции.
При п =О оно переходит в очевидное: lx<0>- х 1:S lx<0>- х 1.
Пусть неравенство (4.7) выполнено при п = т - 1. Тогда
lx(m)_ Х 1:Sqlx<m-I)_Х1:Sqmlx(O)_Х1.
т.е. неравенство выполнено и при п = т. •
Л ем м а 4.2. Пусть одношаговый итерационный метод в некоторой
а-окрестности корня х имеет р-й порядок сходимости, где р > 1.
Пусть о> О таково, что о :S а и СоР - 1 :S 1, где С - постоянная из
неравенства (4.6). Тогда при любом выборе начального приближения
x<0J из о-окрестности корня х итерационная последовательность х<п)
не выходит за пределы этой окрестности, метод сходится и справед­
лива оценка
lx(n) _ Х 1 :S C1qPn, п ~О,
где q = c;l ix<O) _х 1' С1 = с-1/(р- IJ.
(4.8)
До к аз ат ель ст в о. Заметим, что принадлежность х<п) окрестности
(х - о, х +о) является следствием неравенства (4.8). В самом деле, так
как q < с;1 о :::; 1 и 1 :::; рп, то из (4.8) вытекает, что ix<пJ - х 1 :::; С1 q =
= lx<0>- х 1<о. Сходимость х<п) к х также следует из (4.8).
Справедливость неравенства (4.8) установим методом индукции.
При п = О оно переходит в очевидное: lx<0> - х 1:S lx<0J - х 1. Пусть
неравенство (4.8) выполнено при п = т - 1. Докажем, что оно верно и
при п = т. Используя условие (4.6), получаем
lx(m)_ Х 1:S Clx<m-I)_ Х IP :S C(C1qPm-l)p=C1qPm. 8
С помощью доказанных лемм исследование сходимости итерацион­
ных методов сводится только к получению оценки (4.6).
§ 4.2. Обусnовnенность задачи вычисnени1 корн~
Пусть х - корень уравненич (4.1), подлежащий определению.
Будем считать, что входными данными для задачи вычисления корня
х являются значения f(x) функции f в малой окрестности корня. Так
как значения /(х) будут вычисляться на компьютере по некоторой про­
грамме, то в действительности задаваемые значения являются прибли-
93

95. Глава 4. Методы отыскания решений нелинейных уравнений
женными и их следует обозначать через f°(x). Погрешности в значе­
ниях 1•(х) могут быть связаны не только с неизбежными ошибками
округления, но и с использованием для вычисления значений функции
f приближенных методов. К сожалению, нельзя ожидать, что в окрест­
ности корня относительная погрешность fJ(j•) окажется малой. Доста­
точно обратиться к примерам 2.11 и 3.11, чтобы убедиться в том, что
даже для чрезвычайно простых функций у = 1 - х и у = sшх в окрест-
ности корней х = 1 и х = 7t значения этих функции не могут быть
найдены с малой относительной погрешностью. Реально рассчитывать
можно лишь на то, что малой окажется абсолютная погрешность
вычисления значений функции.
Будем предполагать, что в достаточно малой окрестности корня
выполняется неравенство lf(x) - f•(x)I < Л, где Л = Л(!) - граница
абсолютной погрешности. Сама погрешность корня ведет себя крайне
нерегулярно и в первом приближении может восприниматься пользова­
телем как некоторая случайная величина. На рис. 4.3, а представлена
идеальная ситуация, отвечающая исходной математической постановке
задачи, а на рис. 4.3, б - реальная ситуация, соответствующая вычис­
лениям значений функции f на компьютере.
Если функция f непрерывна, то найдется такая малая окрестность
(х - ё, х + ё) корня х, имеющая радиус ё >О, в которой выполняется
неравенство
l/(x)I ;$ л. (4.9)
у
о)
Рис.4.9
94

96. § 4.2. Обусловленность задачи вычисления корня
Для х е (х - "Е, х + "Е) знак вычисленного значения /°(х), вообще
говоря, не обязан совпадать со знаком /(х) и, следовательно, стано­
вится невозможным определить, какое именно значение х из интервала
(х -Е, х + Е ) обращает функцию f в нуль (рис. 4.3, б).
Будем называть этот интервал интервалом неопределенности
корня х .Найдем оценку величины "Е . Пусть корень х - простой. Для
близких к х значений х справедливо приближенное равенство
f(x) ""f(x) +f'(x)(x- х) = f'(x)(x - х).
Поэтому неравенство (4.9) имеет вид l/'(x){x-x)I ::5 Л, откуда полу­
чаем
- -- л - л
х - lf'(x) 1 ::5 х ::5 х + lf'(x) 1 •
Следовательно,
(4.1 О)
1
Здесь vл = lf'(х) I - число, которое в рассматриваемой задаче играет
роль абсолютного числа обусловленности. Действительно, если х • -
корень уравненияj(х) =О, то х• удовлетворяет неравенству (4.9) и тогда
выполнено неравенство
(4.11)
Заметим, что радиус интервала неопределенности прямо пропор­
ционален погрешности Л вычисления значения f Кроме того, Е воз­
растает (обусловленность задачи ухудшается) с уменьшением lf'(x) 1,
т.е. с уменьшением модуля тангенса угла наклона, под которым график
функции пересекает ось Ох (рис. 4.4, а, 6).
Если же f'(x) =О (т.е корень х - кратный), то формула (4.10) уже
не верна. Пусть кратность корня равна т. Тогда в силу формулы Тей­
лора1 справедливо приближенное равенство
f"(x) 1<т>(х)
f(x) ""f(x) +f'(x)(x- х) + -2,- (х - х)2 + ". + -т-,- (х- х)т.
1 Брук Тейлор (1685-1731) - английский математик и философ. Широко известная
формула разложениJI функции в степенной ряд была получена им в 1712 г.
95

97. Глава 4. Методы отыскания решений нелинейных уравнений
у у
х х
2Л
Рис. 4.4
в правой части которого все слагаемые, кроме последнего, равны нулю.
Следовательно, неравенство (4 9) имеет вид
1 f(m~~x) (х - x)ml ;:; л .
Решая его, получаем аналогично (4 10) оценку радиус интервала неоп­
ределенности:
"E:::::j _т_'_l11mл11m.
f(т>(х)
Эта оценка означает, что для корня кратности т радиус интервала
-11т
неопределенности пропорционален Л , что свидетельствует о пло-
хой обусловленности задачи вычисления кратных корней. С этой
неприятностью мы уже сталкивались при рассмотрении примера 3.9.
Отметим, что Е не может быть меньше 1х1 & м - погрешности
-
представления корня х в компьютере.
В реальной ситуации оценить значение и даже порядок радиуса
интервала неопределенности довольно сложно. Однако знать о его
существовании нужно по крайней мере по двум причинам. Во-первых, не
- -
имеет смысла ставить задачу о вычислении корня х с точностью & < & .
В условиях неопределенности, вызванных приближенным заданием
функции, любое значение х• Е (х - Е, х + "Е) может быть с одной и той
же степенью достоверности принято за решение уравнения. Во-вторых,
нельзя требовать от алгоритмов отыскания корня получения достовер­
ных результатов после того, как очередное приближение попало в
интервал неопределенности или оказалось очень близко от него, в этой
96

98. § 4.3. Метод бисекции
ситуации вычисления следует прекратить и считать, что получен мак­
симум действительно возможного.
Для большинства итерационных методов определить этот момент
можно, поскольку начиная с него поведение приближений х<п) стано­
вится крайне нерегулярным. Если вдали от интервала неопределенно­
сти величина
lx(n) _x(n-1)1
q(n) = -'------'-
1х<п-1) - х<п - 2) 1
(4.12)
обычно бывает меньше единицы ( /х<п) - х<п - I) 1 < 1х<п - 1>- х<п - 2) 1), то
появление при некотором п значения q<11J > 1 свидетельствует, скорее
всего, о начале «разболтки» - хаотического поведения итерационной
последовательности. В этой ситуации вычисления имеет смысл пре­
рвать, чтобы выяснить причину явления и принять правильное реше­
ние. Лучшим из полученных приближений к решению следует считать,
конечно, х<п - 1J. Использование для контроля вычислений величины
(4.12) называют часто правилом Гарвика.
§ 4.3. Метод бисекции
1. Описание метода. Пусть требуется с заданной точностью Е > О
найти корень х уравнения (4.1). Отрезок локализации (а, Ь] (т.е. отре­
зок, содержащий только один корень х) будем считать заданным.
Предположим, что функция/непрерывна на отрезке (а, Ь] и на его кон­
цах принимает значения разных знаков, т.е.
f(a)f(b) <О. (4.13)
На рис. 4.5 изображен случай, когда /(а)< О и /(Ь) >О.
Для дальнейшего будет удобно обозначить отрезок [а, Ь] через
[а<0>, ь<0>]. Примем за приближенное значение корня середину отрезка -
Рис. 4.5
97

99. Глава 4. Методы отыскания решений нелинейных уравнений
точку x<OJ = (a<OJ + ь<О>)/2. Так как положение корня х на отрезке
[a<OJ, ь<0>] неизвестно, то можно лишь утверждать, что погрешность
этого приближения не превышает половины длины отрезка (рис. 4.5):
lx(O) - х 1 ~ (Ь(О) _ а<О>)/2.
Уменьшить погрешность приближения можно, уточнив отрезок
локализации, т.е. заменив начальный отрезок [а<0>, ь<0>] отрезком
[аО>, ь<I)] меньшей длины. Согласно методу бисекции (половинного
деления) в качестве [aOJ, ь< 1 >] берут тот из отрезков [а<О>, х<О>] и [х<О>,
ь<0>], на концах которого выполняется условие /(a(l>)f(b<1>) ~ О. Этот
отрезок содержит искомый корень. Действительно, если fla(l>)flb(I)) <О,
то наличие корня следует из теоремы 4.1; если же f(a(l>)f(bO>) =О, то
корнем является один из концов отрезка. Середина полученного
отрезка x(I) = (a(I) + ЬО>)/2 дает теперь приближение к корню, оценка
погрешности которого составляет
lx<1>- х 1 ~ (b(l)_a(l>)/2 = (Ь - а)/22 •
За очередное уточнение отрезка локализации [ащ, ь<2>] снова берут
тот из отрезков [a(I>, x(I>], [х< 1 >, ь(I>], на концах которого выполняется
условие f(a<2>)f(b<2>) ~ О.
Опишем очередную (п + 1)-ю итерацию метода. Пусть отрезок
[а<п>, ь<п>] уже найден и вычислены значения х<п>, f(а<п>), f(Ь<п>). Тогда
производят следующие действия:
1°. Вычисляют f(x(n) ).
2°. Если f(a<n>)f(x<n>) ~ О, то в качестве отрезка локализации
[а<п+ 1), ь<п+ 1)] принимают отрезок [а<п>, х<п>]. в противном случае
f(x(n))f(b(n>) <о и за [а<п + 1>, ь<п +I)] принимают отрезок [х<п>, ь<п>].
3°. Вычисляют х<п + 1>= (а<п +I) + ь<п + 1))/2.
Неограниченное продолжение итерационного процесса дает после­
довательность отрезков [а(О), Ь(О)], (a(I), b(I)], "., [а<п>, Ь(п)], .",содержа­
щих искомый корень. Каждый из них (за исключением начального)
получен делением пополам предыдущего отрезка.
2. Скорость сходимости. Середина п-го отрезка - точка х<п> =
= (а<п> + ь<п>)/2 дает приближение к корню х, имеющее оценку погреш­
ности
(4.14)
Из этой оценки видно, что метод бисекции сходится со скоростью
геометрической прогрессии, знаменатель которой q = 1/2. По сравне­
нию с другими методами метод бисекции сходится довольно медленно.
98

100. §4.3. Метод бисекции
Однако он очень прост и весьма непритязателен; для его применения
достаточно, чтобы выполнялось неравенство (4.13), функция f была
непрерывна и верно определялся ее знак. В тех ситуациях, где не нужна
сверхвысокая скорость сходимости (а это часто имеет место при про­
стых прикладных расчетах), этот метод весьма привлекателен.
Заметим, что число итераций, которое требуется при применении
метода бисекции для достижения разумной точности Е, не может быть
очень большим. Например, для уменьшения первоначального отрезка
локализации в 106 раз нужно 19 итераций.
3 а меч ан и е. Интересно, что при выполнении условия (4.13)
метод бисекции сходится даже, если на отрезке [а, Ь] находится не
один, а несколько корней уравнения f(x) = О. В результате приме­
нения метода будет найден один из этих корней.
3. Критерий окончания. Итерации следует вести до тех пор,
пока не будет выполнено неравенство ь<п> - а<п> < 2Е. При его выпол­
нении в силу оценки (4.14) можно принять х<п> за приближение к
корню с точностью Е.
Пр им ер 4.4. Найдем методом бисекции с точностью Е = 10-2 поло­
жительный корень уравнения 4( 1 - х2) - ех = О.
В примере 4.2 этот корень был локализован на отрезке [О, 1], причем
/(0) > О, f( 1) < 0. Положим а(О) = 0, Ь(О) = 1, х(О) = (а(О) + Ь(О))/2 = 0.5.
1-я итерация. Вычисляемf(х<0>):::: 1.3512. Так какf(а(О))j(х<0>) >О,
то за очередной отрезок локализации принимаем [а(!>, b(I)] = [0.5, 1].
Вычисляем x(IJ = (а< 1 1 + b(I >)/2 = 0.75.
2-я итерация. Вычисляемf(хО>) ::::-0.3670. Так какf(аО>)J(хО>) <
<О, то [а<2), Ь(2)] = [0.5, О. 75] и х<2) = (а<21 + Ь(21)/2 = 0.625.
Результаты следующих итераций (с четырьмя цифрами после деся­
тичной точки) приведены в табл. 4.2.
Таблица 4.2
Номер ите- Знак
a(n) Ь(•) _x{n) л:х<•)> Ь(п) _ a(n)
рации k f(d")) f(b("))
о 0.0000 1.0000 + - 0.5000 1.3513 1.0000
1 0.5000 1.0000 + - 0.7500 -0.3670 0.5000
2 0.5000 0.7500 + - 0.6250 0.5693 0.2500
3 о 6250 0.7500 + - 0.6875 0.1206 0.1250
4 0.6875 0.7500 + - 0.7187 -0.1182 0.0625
5 0.6875 0.7187 + - 0.7031 0.0222 0.0312
6 0.7031 0.7187 + - 0.7109 - 0.0156
99

101. Глава 4. Методы отыскания решений нелинейных уравнений
При п = 6 имеем Ь(б) -а<б)"' 0.0156 < 2 • 10-2. Следовательно, задан­
ная точность достигнута и можно принять х :::ох<6>. Окончательно полу­
чим х = 0.71 ±О.О . .А
4. Влияние вычислительной погрешности. При использовании
метода бисекции принципиально важным является правильное опреде­
ление знака функции f В случае, когда х<п> попадает в интервал неоп­
ределенности корня (см. § 4.2), знак вычисленного значения] (x<n>) не
обязан быть верным, и последующие итерации не имеют смысла.
Однако этот метод следует признать очень надежным; он гарантирует
точность приближения, примерно равную радиусу интервала неопреде-
ленности &. Как было отмечено в § 4.3, большего требовать нельзя.
§ 4.4. Метод простой итерации
1. Описание метода. Чтобы применить метод простой итерации
для решения нелинейного уравнения (4.1 ), необходимо преобразовать
это уравнение к следующему виду:
х = <р(х). (4.15)
Это преобразование (приведение уравнения к виду, удобному для итера­
ций) можно выполнить различными способами; некоторые из них будут
указаны ниже. Функцию <р далее будем называть итерационной функ­
цией.
Выберем каким-либо образом приближенное значение корня х<0>
и подставим его в правую часть уравнения (4.15). Получим значение
х< 1 > = <р(х<0>). Подставляя теперь х< 1 > в правую часть уравнения (4.15),
имеем х<2> = <р(х< 1 >). Продолжая этот процесс неограниченно, получаем
последовательность приближений к корню, вычисляемых по формуле
х<п + 1) = <p(x<n>), п ~ О. (4.16)
Очевидно, что метод простой итерации - одношаговый (см. § 4.1).
Если существует предел построенной последовательности х =
lim х<п), то, переходя к пределу в равенстве (4.16) и предполагая
функцию <р непрерывной, получаем равенство
х=<р(х).
Это значит, что х - корень уравнения (4.15).
100
(4.17)

102. § 4.4. Метод простой итерации
х
Рис. 4.6
2. Геометрическая иллюстрация. Из рис. 4.6 видно, что корень х
уравнения (4.15) является абсциссой точки пересечения графиков двух
функций: у= х и у= <р(х). Возьмем некоторое начальное приближение
х(О>, которому отвечает расположенная на кривой у = <р(х) точка М(О)
с координатами (х(О>, хО>) (напомним, что хО> = <р(х(О))). Соединим
точку М(О) отрезком прямой у= x(I) с лежащей на прямой у= х точкой
N(I) с координатами (хО>, хО>). Проведем теперь через точку N(I) пря­
мую х =хО> до пересечения с кривой у = <р(х) в точке M(I) с координа­
тами (хР>, х<2>). Продолжая этот процесс далее, получаем ломаную
линию M(O)NP)M0)N(2)M(2) ... , для которой абсциссы точек М(п) пред-
ставляют собой последовательные приближения х<п> к решению х .
3. Сходимость метода. На рис. 4.7, а--г представлена геометриче­
ская иллюстрация поведения итерационного процесса в четырех про­
стейших случаях взаимного расположения прямой у = х и кривой у =
= <р(х).
Рисунки 4.7, а и б иллюстрируют случаи, когда метод простой ите­
рации сходится, причем, как нетрудно заметить, - при произвольном
начальном приближении. Напротив, рисунки 4.7, в и г иллюстрируют
случаи, когда метод расходится при любом выборе начального приближе-
ния х(О) -F- х. Заметим, что на рис. 4.7, а и б /<р'(х)/ < 1 (модуль тангенса
угла наклона кривой у = <р(х) к оси абсцисс меньше единицы), а на
рис. 4.7, в и г, наоборот, /1р'(х)/ > 1. Таким образом, можно предполо­
жить, что сходимость метода простой итерации связана с выполнением
условия /<р'(х) 1 < 1. Действительно, имеет место следующий результат.
101

103. Глава 4. Методы отыскания решений нелинейных уравнений
у
х
х
Рис. 4.7
Теорема 4.2. Пусть в некоторой а-окрестности корнях функция
<р дифференцируема и удовлетворяет неравенству
l<i>'(x)I::;; q, (4.18)
где О ::;; q < l - постоянная.
Тогда независимо от выбора начального приближениях<ОJ из указан­
ной а-окрестности корня итерационная последовательность не выхо­
дит из этой окрестности, метод сходится со скоростью геометриче­
ской прогрессии и справедлива следующая оценка погрешности:
lх<п) - х 1::;; q" lx<0>- х 1. (4.19)
Доказательство. Вычитая из равенства (4.16) равенство (4.17) и
используя формулу конечных приращений Лагранжа, получаем
х<п+ I)_ х = <р(х<11>)-<р(х) = а<п+ 1 >(х<11>- х ). (4.20)
Здесь а<" + 1> = <р'(~ <11>), где ~(п) - некоторая точка, расположенная
между х<п) и х. Если х<п) е (х - cr, х + cr}, то 1а<"+ I) 1 ::;; q в силу усло­
вия (4.18). Тогда на основании равенства (4.20) получаем
lx<n+l) _ _i 1::;;qlx(n)_х1.
102

104. § 4.4. Метод простой итерации
Это означает, что метод простой итерации обладает линейной скоро­
стью сходимости и поэтому доказательство теоремы завершается при­
менением леммы 4.1. •
Оценка погрешности (4.19) является априорной. Она показывает, что
метод простой итерации сходится со скоростью геометрической прогрес­
сии, знаменатель которой равен q. Чем меньше q, тем выше скорость схо­
димости. Видна и роль правильного выбора начального приближения:
чем меньше погрешность начального приближения, тем меньше итера­
ций потребуется сделать для достижения заданной точности е.
Неравенство (4.19), как правило, не используется для практической
оценки погрешности. Одна из причин этого состоит в том, что значение
х ,входящее в правую часть оценки, неизвестно. Кроме того, использо­
вание неравенства (4.19) приводит к существенно завышенной оценке
погрешности.
4. Критерий окончания. Выведем апостериорную оценку погреш­
ности, пригодную для практического применения.
Теорема 4.3. Пусть выполнены условия теоремы 4.2 и x<D> е
е (х - а, х + cr). Тогда верна следующая апостериорная оценка
погрешности:
ix<п>-xi :$-1q iх<п>-х<п- 1 >1, п~ 1.
-q
Доказательство. В силу равенства (4.20) имеем
(4.21)
х<п) _ х = а<п>(х<п - l) _ х) = а<п>(х<п - l) _ x<n>) + а<п>(х<п) _ х ).
Откуда
а(п)
х<п>- х = --- (х<п-1) _х<n>).
1 -а<п)
(4.22)
Взяв модуль от левой и правой частей этого равенства и воспользо­
вавшись неравенством 1~1:$ ~, получим требуемое соотноше-
1- а(п) -q
ние (4.21). 8
Если значение q известно, то неравенство (4.21) дает эффективный
метод контроля погрешности и можно сформулировать следующий
критерий окончания итерационного процесса. Вычисления следует
вести до выполнения неравенства _q_ 1х<п> - х<п- 1J1 < е или равно-
1- q
сильного ему неравенства
1-q
iх<п>-х<п-1) 1< - Е.
q
(4.23)
103

105. Глава 4. Методы отыскания решений нелинейных уравнений
Если это условие выполнено, то найденное значение х<п> является при­
ближением к х с точностью Е.
Пр им ер 4.5. Используем метод простой итерации для вы числе­
ния положительного корнях уравнения4(1 -х 2)-ех =О с точностью
Е = 10-4• Результат примера 4.4 дает для корня отрезок локализации
[а, Ь] = (0.70, 0.72).
Преобразуем уравнение к виду (4.15), где q>(x) = J1- ех/ 4. Заме­
тим, чтоq>'(х) = -ex/(8JI -ex/4),q>"(x) =-ex(1-ex/8)/(8J1 -ех/4)3 .
Так как q>" < О на [а, Ь], то производная q>' монотонно убывает и q =
= maxlq>'(x)I =q>'(b)"" 0.37. Следовательно, условие сходимости (4.18)
[а,Ь]
выполнено. Возьмем х<0> = О.7 и будем вести итерации до выполнения
критерия (4.23). В табл. 4.3 соответствующие приближения приведены
с десятью знаками мантиссы.
п
о
2
3
4
5
х<п)
0.7000000000
0.7046714292
о.7029968319
0.7035984939
о. 7033824994
0.7034600632
Таблица 4.3
3. 10-з
1·10-3
4· J0--4
2· 10--4
5 • 10-5
Критерий окончания выполняется при п = 5. После округления зна­
чения х<5> до четырех значащих цифр получим х = О.7035 ± О.ООО1. .&
104
Замечание. Часто в практике вычислений вместо критерия
(4.23) используется привлекательный своей простотой критерий
lx(n)_x(n-) 1 <Е. (4.24)
В случае О < q ~ 1/2 использование критерия (4.24) оправдано.
Действительно, здесь (1 - q)/q ~ 1 и поэтому выполнение неравен­
ства (4.24) влечет за собой выполнение неравенства (4.23).
В то же время при 1/2 < q < 1 использование критерия (4.24)
может привести к преждевременному прекращению итераций.
Дело в том, что когда значение величины q близко к единице, ите­
рационный процесс сходится медленно и расстояние между двумя
последовательными приближениями х<п) и х<п - I) не характеризует
расстояние от х<пl до решения х (рис. 4.8).

106. § 4.4. Метод простой итерации
Рис. 4.8
Пр им ер 4.6. Пусть метод простой итерации используется для реше­
ния уравнениях= О.9999х + 10-4; J2. Здесь <р(х) = О.9999х + I0-4/ J2,
<р'(х) = 0.9999 и, следовательно, условие (4.18) сходимости метода
выполнено. Для вычислений по формуле (4.16) используем 6-разряд­
НЬ1Й десятичный компьютер. Возьмем х<0> = 0.715010. Тогда x(I) =
= 0.715009 и, если доверять критерию (4.24), то следовало бы считать,
что решение получено с точностью Е = 10-6. Продолжая вычисления,
имеем х<2> = 0.715008, х<3> = 0.715007, х<4> = 0.715006, х<5> = 0.715005,
х<6> = 0.715005. Дальнейшие итерации теряют смысл. Сколько же верных
знаков найдено? Сравнение с точным значением решения х = 1/ J2 =
= 0.707106 ". показывает, что верными в приближении х<6> являются
только две значащие цифры. Использование критерия (4.24) в данном
случае категорически недопустимо. В дальнейшем мы еще вернемся
к обсуждению этого примера. •
Использование критерия (4.23) предполагает знание значения вели­
чины q, входящей в условие (4.18). Однако далеко не всегда это значе­
ние известно, либо может быть легко вычислено. В тех же случаях,
когда удается оценить q, эта оценка оказывается довольно грубой.
Исключим из критерия окончания итераций величину q. Заметим, что
в малой окрестности корня значение производной <р' практически посто-
янно: <р'{х) "'<р'(х ). Поэтому в равенстве (4.22) величину а<п> = <p'(l;<n- I!)
можно приближенно заменить на <р'(х ). Далее в силу равенства
х<п>-х<п-1) =<p(x<n- l>)-<p(x<n-2>) = <р'(~<п>)(х<п- l)_х(п-2)),
105

107. Глава 4. Методы отыскания решений нелинейных уравнений
где ~(п) - промежуточная между х<п - I) и х<п - 2> точка, имеем
x<n) _x(n-1) - _
(i(n) = <р'(~(п)):::;<р'(х).
х<п-1>-х<п-2)
Таким образом, в равенстве (4.22) можно положить а<п> "" (i<п> и
поэтому при определенных условиях можно использовать следующий
практический критерий окончания итерационного процесса:
lх<п>-х<п-1)1~11 ::a<n)IE.
а(п)
S. Дополнительные сведения о характере сходимости. Когда про­
изводная <р' знакопостоянна на отрезке локализации, итерационная
последовательность обладает некоторыми полезными дополнитель-
ными свойствами. Заметим, что при <р'(х) * О в достаточно малой
окрестности корня знак производной <р'(х) действительно постоянен.
Теорем а 4.4. Пусть [а, Ь] - отрезок локализации корня уравнения
(4.15). Предположим, что на этом отрезке функция <р непрерывно
дифференцируема, а ее производная <р'(х) знакопостоянна и удовлетво­
ряет неравенству (4.18) при О< q < 1. Пусть х<0> Е [а, Ь] - произволь­
ное начальное приближение и при <р' < О выполнено дополнительное
условие х< 1 > = <р(х<0>) Е [а, Ь] (первое приближение не выходит за пре­
делы отрезка локализации).
Тогда итерационная последовательность не выходит за пределы
отрезка [а, Ь], метод простой итерации сходится и верны оценки погреш­
ности (4.19), (4.21). Краме того, справедливы следующие свойства:
1°. Если <р' >О на [а, Ь], тох<п) сходится к х, монотонно возрастая
при а ~ х<О) < х ,и монотонно убывая при х < х<О) ~ Ь.
2°. Если <р' <О на [а, Ь], то сходимостьх<п) к х носит колебатель­
ный характер, т.е. при всех п ~ О значения х<п) и х<п + 1) расположены
по разны1: стороны от х, причем последовательности приближений
с четными и нечетными номерами сходятся к х монотонно. В этом
случае верна апостериорная оценка погрешности
lx(n)_ х 1 ~ lx<nJ_x(n- l)I, п ~ 1 (4.25)
и справедлив критерий (4.24) окончания итерационного процесса.
Мы не будем приводить здесь полное доказательство теоремы. Оно
основано на использовании равенства (4.20), установленного при доказа­
тельстве теоремы 4.2. Докажем только справедливость свойств 1° и 2°.
106

108. § 4.4. Метод простой итерации
Доказательство. Если О < q>' ::; q, то знаки величин х<п> - х
и х<п - I) - х совпадают, в то время как lx(n)_ х 1::; q /х<п- I) _ х 1. Сле­
довательно, последовательность монотонно приближается к х с той
стороны, где лежит х<0>. Если же -q < q>' <О, то из равенства (4.20) сле­
дует, что знаки величин х<п> - х и х<п - 1>- х различны. Это подтвер­
ждает колебательный характер сходимости. •
Замечание. Монотонный и колебательный характер сходимо­
сти итерационной последовательности, указанные в теореме 4.4,
иллюстрируют соответственно рис. 4.7, а и 6.
6. Приведение уравнения к виду, удобному для итераций. Клю­
чевой момент в применении метода простой итерации - эквивалент­
ное преобразование уравнения (4.1) к виду (4.15). Конечно, такое пре­
образование имеет смысл только тогда, когда оказывается
выполненным условие (4.18) с О< q < 1. Укажем один из простых спо­
собов такого преобразования.
Предположим, что производная f' на отрезке [а, Ь] непрерывна
и положительна. Тогда существуют положительные постоянные т и М
такие, что О< т::; f(x)::; М, хе [а, Ь]. Приведем уравнение (4.1) к виду
х = х - af(x), (4.26)
где а > О. Здесь итерационная функция q> имеет вид q>(x) = х - af(x).
Как выбрать а, чтобы выполнялось условие (4.18), причем q было бы
по ВОЗМОЖНОСТИ минимальным?
Заметим, что 1 - аМ ::; q>'(x) = 1 - af' (х) ::; 1 - ат и поэтому
lч>'(x)I::; q(a) = max{ l 1-aMI, l I -aml }. Для того чтобы было выпол­
нено неравенство q(a) < 1, достаточно взять любое а е (0,2/М). Кон­
кретный выбор параметра а зависит от наличия информации о числах т
и М. Если известны обе эти величины, то лучшим является выбор а =
=а 0 = 2/(М+ т). В этом случае q(a0 )=(M-m)/(M+ т). Если же известно
только М, то можно положить а= а 1 = IM. В этом случае q (а1 )= 1- т!М.
Кроме того, при а= а 1 производная q>'(x) неотрицательна, и в силу тео­
ремы 4.3 сходимость является монотонной.
1
3 а меч ан и е. Случай, когда производная f' отрицательна, сво­
дится к рассмотренному выше умножением уравнения f(x) = О на -l.
Пример 4.7. Для решения задачи, поставленной в примере 4.5,
можно воспользоваться преобразованием уравнения (4.4) к виду
(4.26). Будем считать известным, что х е [О. 70, О. 72]. Так как на
отрезке локализации выполнено условие (4(1 - х2)- еХ)' =-8х - еХ <О,
107

109. Глава 4. Методы отыскания решений нелинейных уравнений
то перепишем уравнение в видеfj(х) =О, гдеfj(х) = е'" - 4(1 - х2). Тогда
fj (х) = е'" + 8х и для х е [О. 70, О. 72) верны оценки О < т = fj (О. 70) s
s fi (х) $ fj (0.72) = М. Выберем в уравнении (4.26) а= 2/(т + М), возь­
мемх<0> = 0.7 и будем вести итерации по формулех<п + 1) =x(n) - а[е·«п> -
- 4(1 - (х<11>) 2 )]. Выбранному а соответствует q =(М- т)!(М+ т)""
"" О.О 13 и поэтому сходимость должна быть более быстрой, чем в при­
мере 4.6. Действительно, уже первая итерация дает хО> = О.7034025118,
и так как _q_ lx<1>- х<0> 1 "" 5 • 10-5, то итерации следует прекратить
1-q
и считать х = 0.7034 ±О.ООО. А.
§ 4.5. Обусповnенность метода простой итерации
В § 4.4 метод простой итерации был рассмотрен при идеальном
предположении о возможности точного вычисления значений функции
<р(х). В действительности же вычисления на компьютере дают прибли­
женные значения <р•(х). Поэтому вместо последовательности x<n>, удов­
летворяющей равенству х<11 + l) =<р(х(11>), получается последовательность
:Х<11>, для которой
(4.27)
Известно, что метод простой итерации и многие другие итерацион­
ные методы устойчивы к ошибке, допущенной на одной из итерации.
Такая ошибка эквивалентна некоторому ухудшению очередного при­
ближения; если она не вывела приближение за пределы области сходи­
мости, то итерационная последовательность по-прежнему будет схо-
диться к решению х ,а внесенная погрешность - затухать. Поэтому о
таких итерационных методах говорят, что они обладают свойством
самоисправляемости.
Однако погрешности допускаются не на одной, а на всех итерациях
и совокупное их влияние несколько иное.
1. Обусловленность задачи. Прежде чем сформулировать резуль­
тат о поведении метода простой итерации при наличии погрешности в
вычислении функции <р, отметим, что преобразование уравнения f(x) = О
к виду х = <р(х) изменяет обусловленность задачи. Запишем это уравне-
- -ние в виде f(x) =О, где f(x) = х - <р(х), и воспользуемся результатами
§4.2. Заметим, что ЛJ')=Л(<р'), поскольку в действительности при-
108

110. § 4.5. Обусловленность метода простой итерации
ближенно вычисляется только функция <р. Поэтому оценка (4. l l) в дан­
ном случае выглядит так:
Л(х·) ~ &""vЛ(<р•). (4.28)
Здесь v = l/l l -<р'(х )1 - абсолютное число обусловленности корнях.
Грубо оценивая при выполнении условия 1<р'1 ~ q < l величину v чис­
лом v= 1/(1 - q), приходим к оценке
Л(х·);::; Л(<р').
-q
(4.29)
Когда <р' ~ О или <р' о:: О, ее можно уточнить. Действительно, как
нетрудно установить, v :$ l, если <р' :$ О; следовательно,
Л(х·);::; Л<<р.). (4.30)
Заметим, что в оценках (4.28Н4.30) величины Л(х') и Л(<р') можно
заменить на Б(х') и Б(<р') . Чтобы убедиться в этом, дост1ПОчно разде­
лить левую и правую части оценок на величины 1х 1 и 1<р( х) 1, которые
равны между собой. Например, оценка (4.28) преобразуется к виду
(4.3 l)
и, следовательно, абсолютное и относительное числа обусловленности
здесь совпадают.
Сделаем некоторые выводы. Задача вычисления корня х уравнения
х = <р(х) плохо обусловлена, если <р'(х)"" 1. В этом случае следует ожи­
дать, что количество верных цифр корня х по сравнению с количест­
вом верных цифр в вычисляемых значениях <р•(х) должно быть меньше
примерно на N = lgv цифр. Для радиуса интервала неопределенности
Е о:: vЛ( <р') корня х при 1<р' 1 ~ q < 1 справедлива оценка &~ &• =
= Л(<р') . Когда -1 < <р' ~ О, уточненная оценка такова. Е :$ Е• = Л(<р');
-q
здесь потери верных цифр быть не должно.
Пример 4.9. Для уравнениях =<р(х) при<р(х) =О.9999х + 10-4;.fi
имеем <р'(х) = 0.9999 и, следовательно, v = 104. Поэтому при решении
этого уравнения методом простой итерации на компьютере будет поте­
ряно примерно четыре значащих цифры. Вычисления на 6-разрядном
десятичном компьютере (или на близком ему по точности компьютере
типа IBM РС) могут дать всего лишь две верные значащие цифры. Это
вполне согласуется с результатом, полученным в примере 4.6. А
109

111. Глава 4. Методы отыскания решений нелинейных уравнений
2. Чувствительность метода простых итераций к погрешности
вычислений. Сформулируем основной результат данного параграфа.
Теорема 4.5. Пусть выполнены условия теоремы 4.2 и для всех
х е ( х - cr, х + cr) имеет место неравенство 1<р(х) - q) (х)1 s Л(<р•).
-· Л(qi•) - •
Предположим также, что Е =-- < cr (т.е. величина Л(<р ) доста-
1 - q
точно мала).
Если вычисления по формулам (4.16) и (4.27) начинаются с одного
начального приближения х<0> = x<0>e(x-cr1,x+cr1), где cr1=
cr-E -
{ -·}= min cr, -q- , то последовательность х <п> не выходит за пределы
-
а-окрестности корня х и для всех п ~ 1 справедливы следующие
оценки погрешности:
/х<п>-х<п>/ s е·'
/х<п>-х / S qn/x<0>-x 1 + е•,
lх<п>-х/ sс1:Х<п>-:Х<п-1>1 +е•;
(4.32)
(4.33)
(4.34)
здесь С = _q_ .
1-q
Замечание 1. При <р' s О в неравенствах (4.32)-(4.34) можно
положить е·~Л<ч>*), с~ 1.
Замечание 2. При достаточно больших п в оценках (4.32)-
(4.34) величину ё* можно считать приближенно равной радиусу
интервала неопределенности е = Л(~:~).1- q> х
До к аз ат ель ст в о. Докажем по индукции, что для всех п ~ О спра­
ведливы неравенства (4.32), (4.33) и :Х<пJ е (х - cr, х +cr). Очевидно, что
при п = О это верно.
Предположим, что доказываемое утверждение справедливо при
некотором п ~ О. Вычитая из равенства (4.27) равенство (4.16), полу­
чаем
:Х<п + ~>-х<п+ i >=<р'(~<п>н:Х<п>-х<п>) + Л1п>, ~(п> е (х - cr, х + cr),
где Л<п>=<р*(х<п>)-<р(х<п>), /Л!n>/ sЛ(<р*).
110

112. § 4.5. Обусловленность метода простой итерации
Как следствие полученного равенства и сделанных предположе­
ний имеем
lx<n+l)_x(n+l)I ~qlx<n)_x<п>I + 1Л<п>I ~q&•+Д(<р')=&·.
Обьединяя эту оценку с оценкой (4.19), получаем
lx<n+1>-xl ~qп+11;<0>-х +&·.
Учитывая, что х<0>-х <cr1 , имеем
lх<п + 11- х 1< qa1 + &• ~ q(а - е•) +&•=а.
q
Нужное утверждение доказано для номера, равного п + 1, а следова­
тельно, и для всех п 2': О.
Вычитая из равенства (4.27) равенство (4.17), получаем
х<п+ ) _ х = а<п>(х<п) _ х) + Л<п), а<п> = <р'(~<п)), ~(п) Е (х -а, х + cr).
Таким образом,
- - a(n) - - Л<п)
х<п+ I) _ Х = --- (х(п)_х(п+ 1>) + --- .
1- а(п) 1 - а<п)
Из полученного равенства вытекает оценка (4.34). •
Итак, метод простой итерации обладает такой же чувствительно­
стью к погрешностям в вычислении функции <р, что и задача вычисле­
ния корня уравнения х = <р(х). Метод позволяет получить приближен-
-
ное значение корня х с точностью, примерно совпадающей с
радиусом & интервала неопределенности корня. Критерий (4.23) окон­
чания итераций применим, если Ё « в (радиус интервала неопреде­
ленности много меньше заданной точности); это следует из неравен­
ства (4.34) и замечания 2.
Входящую в соотношения (4.29), (4.30) величину Л(<р°) в общем
случае оценить сверху достаточно сложно. Оценка снизу очевидна:
Л(<р•);:: 1х1 Ем. В благоприятной ситуации, когда вычисления ведутся
по простым формулам, можно надеяться на то, что Л(<р•) окажется
величиной порядка 1х 1в м .
111

113. Глава 4. Методы отыскания решений нелинейных уравнений
§ 4.6. Метод Ньютона
Знаменитый метод Ньютона является одним из наиболее эффектив­
ных методов решения самых разных нелинейных задач. Расчетную
формулу метода можно получить, использовав различные подходы.
Рассмотрим два из них.
1. Метод касательных. Выведем расчетную формулу метода для
решения нелинейного уравнения (4.l) из простых геометрических
соображений. Соответствующая иллюстрация приведена на рис. 4.9.
Пусть х<0> - заданное начальное приближение к корню х .В точке
м<0> с координатами (х<0>, J(x<0>)) проведем касательную к графику
функции у = f(x) и за новое приближение х <1) примем абсциссу точки
пересечения этой касательной с осью Ох. Аналогично, за приближение
х<2> примем абсциссу точки пересечения с осью Ох касательной, прове­
денной к графику в точке М(I) с координатами (x(IJ, f(x<1>)). Продолжая
этот процесс далее, получим последовательность х<0>, x(I >, х(2), "., х<11>, ".
приближений к корню х .
Напомним, что уравнение касательной, проведенной к графику
функции у = f(x) в точке (х<11>, f(x<11))), имеет вид
у = f(x<11>) +f'(x<11>)(x - х<11>). (4.35)
Пусть f'(x<11>) *- О. Полагая в равенстве (4.35) у= О, замечаем, что абс­
цисса х<11 + 1> точки пересечения касательной с осью Ох удовлетворяет
равенству
О= J(x<11>) +f'(x<11>)(x<11 + I) -х<11>). (4.36)
Рис. 4.9
112

114. § 4.6. Метод Ньютона
Выражая из него х(п + 1>, получаем расчетную формулу метода Нью­
тона:
х<п + 1) = х<п) - j(x(n>)
f'(х<п)),
п ~О. (4.37)
Благодаря такой геометрической интерпретации этот метод часто
называют методом касательных.
2. Метод линеаризации. С более общих позиций метод Ньютона
можно рассматривать как итерационный метод, использующий специ­
альную линеаризацию задачи и позволяющий свести решение исход­
ного нелинейного уравнения к решению последовательности линейных
уравнений.
Пусть приближение х<п) уже получено. Представим функцию в окре­
стности точки х<п) по формуле Тейлора:
f(x) =J(x<n>) +f'(х<п>)(х -x<n>) +!''~О (х -x<n>)2. (4.38)
Здесь ~ - некоторая точка, расположенная между х и x<nJ. Заменяя
в уравнении f(x) = О функцию /(х) главной линейной частью разложе­
ний (4.38), получаем линейное уравнение
f(x<n>) +f'(x<n>)(x - x<n>) = О. (4.39)
Принимая решение уравнения (4.39) за новое приближение х<п + 1J, при­
ходим к формуле (4.37).
3. Основная теорема о сходимости метода Ньютона.
Теорема 4.6. Пусть х - простой корень уравнения f(x) =О, в
некоторой окрестности которого функция f дважды непрерывно диф­
ференцируема Тогда найдется такая малая а-окрестность корня х ,
что при произвольном выборе начального приближения х<0> из этой
окрестности итерационная последовательность метода Ньютона не
выходит за пределы окрестности и справедлива оценка
lx<n+I)_xl ~а- 1 !х<п>-хl 2 • п~О,
означающая, что метод сходится с квадратичной скоростью.
Следствием оценки (4.40) является априорная оценка
lx(n) _ х 1 ~ aq2", п ~О,
в которой q = a- 1lx(O) _ х j.
(4.40)
(4.41)
113

115. Глава 4. Методы отыскания решений нелинейных уравнений
Доказательство. Так как f'(x) ~ О (по определению простого
корня), то в силу непрерывности функций f' и/" найдется о 0-окрест­
ностъ корня, в которой при некоторых постоянных а и ~ выполнены
неравенства О < а :S 1/'(х) I, lf"(x}1:S ~.
Пусть х<п) е (х - cr, х + cr ), где cr = min{o0 , 2а/~}.
Подставляя х = х в (4.38), получаем равенство
О= f(x<n>) +/'(х<11>)(х -x<n>) + /'~~) (х -x<n))2,
в котором~ е (х - cr, х + cr ). Вычитая из него равенство (4.36), имеем
/' (х<п>)(х<п + 1) - Х ) = !"~~) (Х - x<n>)2.
Тогда, приравнивая модули обеих частей этого равенства и используя
условия ограниченности lf'(х) 1и I/"(х) 1, приходим к неравенству
alx(n+I)_xl :S~lx<п>-xl 2 ,
откуда следует справедливость оценки (4.40). Доказ~rrельство теоремы
завершается применением леммы 4.2. 8
Таким образом, при выборе начального приближения из достаточно
малой окрестности корня метод Ньютона сходится квадратично. Это
означает, грубо говоря, что на каждой итерации число верных цифр
приближения примерно удваивается.
Приведенные в теореме 4.6 оценки погрешности являются априор­
ными (см § 3.3) и их использование в практике вычислений для количе­
ственной оценки погрешности неэффективно или чаще всего невоз­
можно.
4. Критерий окончания. На практике предпочтительнее использо­
вание простой апостериорной оценки
(4.42)
справедливость которой обосновывается следующим утверждением.
Теорем а 4.7. Пусть выполнены условия теоремы 4.6 и 1х<0> - х 1 <
< cr/2. Тогда для всех п ~ 1 верна оценка (4.42).
Доказательство. Из оценки (4.41) следует, что
lx<n-I>-xl :Saq2n-1 :Scrq= lxlO>-xl <~.
114

116. § 4.6. Метод Ньютона
Поэтому, применяя неравенство (4.40), получаем цепочку неравенств
2 lx<n) - х 1s; 2cr-l lx<n -1) _ х 12 s; lx<n-1) _ х 1s;
s; lx(n-l)_x(n)I + lx(n)_ х i,
из которой вытекает оценка (4.42). •
Наличие оценки (4.42) позволяет сформулировать следующий прак­
тический критерий окончания итераций метода Ньютона. При заданной
точности Е > О вычисления нужно вести до тех пор, пока не окажется
выполненным неравенство
lx<п>-x<n-l)I < Е. (4.43)
Пр им ер 4.8. Используя метод Ньютона, найдем с точностью
Е = 1о- 6 положительный корень уравнения 4(1 -х2) - ех = О.
В примере 4.2 корень был локализован на отрезке [О, ).Для f(x) =
=4(1 - х2) - еХ имеем /'(х) = -8х - еХ. Очевидно, что f'(x) * О, т.е.
х - простой корень. Возьмем начальное приближение х<0> = 0.5 и
будем выполнять итерации метода Ньютона по формуле
х<п + 1) = х<п) + 4( 1 - (x<n>)2)- e-"(n)
8х(п) + ex(n)
Результаты первых итераций с десятью знаками мантиссы приведены
в табл. 4.4.
Таблица 4.4
п х<•> /х<•>-х<•- 1 >/
о о. 5000000000
0.7392185177 2.4· 10-1
2 о. 7042444088 3.5. 10-2
3 о. 7034399951 8.0·lo-4
4 1
о. 7034395712 4.3. 10-7
При п = 4 вычисления следует прекратить и после округления полу­
чим х = 0.703440 ± 0.00000.
Сравнение результатов итераций со значением х показывает, что
приближения x<I), хщ, х<ЗJ содержат одну, три, шесть верных значащих
цифр соответственно. Можно показать, что приближение х<4> содержит
десять верных цифр. Это подтверждает отмеченный ранее общий факт:
при каждой итерации метода Ньютона число верных значащих цифр
примерно удваивается. А
115

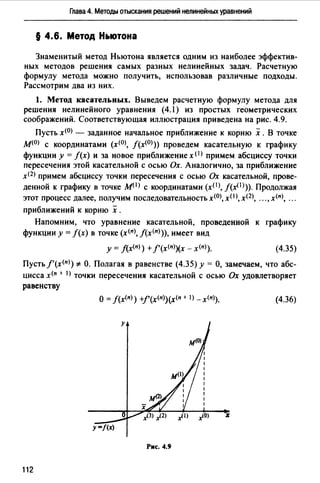
117. Глава 4. Методы отыскания решений нелинейных уравнений
Пр им ер 4.9. Используя метод Ньютона, укажем итерационный
процесс вычисления PJa, где а > О, р - натуральное число.
По определению, х = PJa - это неотрицательная величина, удовле­
творяющая равенству хР = а. Таким образом, задача сводится к вычис­
лению положительного корня уравнения f(x) = О, где /(х) = хР - а.
Итерационная формула метода Ньютона примет вид
(х<">)Р - а - 1
х<" + 1) =х<п) - =Р__ х(п) + а (4.44)
р(х<">)Р - 1 р p(x<n>)p-1
При р = 2 эта формула уже была получена в примере 3.17. А
5. Связь с методом простой итерации. Метод Ньютона можно рас­
сматривать как один из вариантов метода простой итерации, связанный
со специальным преобразованием уравнения f(x) =О к виду
х = q>н(х), (4.45)
где q>н(х) = х - f(x)/f'(x).
Действительно, итерационная формула метода простой итерации
.x(n+ 1) = q>н(х<")) совпадает с (4.37).
Если исходить из этого с учетом оценки (4.19), можно сделать вывод
о том, что метод Ньютона сходится только линейно. Однако заметим,
f"(x)
что q>Л, (х) =f(x) ---2 • Так как f(x) = О, то q>Л,(х) = О и величина
(f'(x))
а<п + I) = 1q>'(~<11))1. определяющая в силу равенства (4.20) коэффициент
сжатия погрешности, стремится к нулю при п ---+ оо. Скорость сходимо­
сти возрастает по мере приближения к корню, отсюда и ее сверхлиней­
ный характер.
В качестве аналога теоремы 4.4 для метода Ньютона приведем сле­
дующий результат.
Теорема 4.8. Пусть [а, Ь] - отрезок локализации простого корня
х уравнения (4.1). Предположим, что на этам отрезке функция f два­
жды непрерывно дифференцируема, а ее производные/'(х) иf''(х) знако­
постоянны. Пусть х<О) е [а, Ь] - произвольное начальное приближение,
и в случае f(x<0))f'(x<0)) < О выполнено дополнительное условие x<I) е [а,
Ь] (первое приближение не выходит за пределы отрезка локализации).
Тогда начиная с п = l итерационная последовательность метода
Ньютона х<11) сходится к х монотонно с той стороны отрезка [а, Ь],
где f(x)f"(x) > О. •
116

118. § 4.6. Метод Ньютона
Иллюстрацией монотонного характера сходимости может служить
рис. 4.9.
Следствие. Пусть уравнение f(x) иuеет корень х, функция f(x)
дважды непрерывно диффере11цируе.ма на всей числовой оси, а ее про­
изводные/' и/" знакопостоянны. Тогда .~1етод Ньютона сходится при
любом 11ачальном приближении х<0> (т.е. является глобально сходя­
щимся), причем начиная с п = 1 последовательность сходится моно­
тонно с той стороны от корня, где f(x)f"(x) > О.
6. Трудности использования. Простота, логическая стройность
и высокая скорость сходимости делают метод Ньютона чрезвычайно при­
мекательным. Однако для его практического применения нужно преодо­
леть две существенные трудности. Одна из них состоит в необходимости
вычисления производной /'(х). Часто бывает невозможно найти аналити­
ческое выражение для f'(x), а определить приближенное значение с
высокой точностью очень трудно. Иногда вычисление f'(x) - вполне
реальная, но весьма дорогостоящая операция. В этих случаях приходится
модифицировать метод, избегая непосредственного вычисления произ­
водной. Некоторые из таких модификаций приведены в§ 4.7.
Более существенно то, что метод Ньютона обладает, вообще говоря,
только локальной сходи:wостью. Эrо означает, что областью его сходимости
-
ямяется некоторая малая а-окрестность корня х и для гарантии сходимо-
сти необходимо выбирать хорощее начальное приближение, попадающее в
эту а-окрестность. Неудачный выбор начального приближения может дать
расходящуюся последоВ<Пельность (рис. 4.1 О) и даже привести к прежде­
временному прекращению вычислений (если на очередной итерации
f' (х<п>) "' О). Для преодоления этой трудности часто используют метод Нью­
тона в сочетании с каким-либо медленно, но гарантированно сходящимся
методом типа бисекции. Такие гибридные алгоритмы находят в последнее
время широкое практическое применение.
у
Рис. 4.10
117

119. Глава 4. Методы отыскания решений нелинейных уравнений
7. Влияние погрешности вычислений. Пусть х - простой
корень. Если метод Ньютона рассматривать как вариант метода простой
итерации, связанный с преобразованием уравнения f(x) = О к виду
(4.45), то можно воспользоваться результатами § 4.4 и 4.5.
Поскольку <рЛr(х) =О, то справедливо неравенство (4.30) и радиус
интервала неопределенности &N корня х преобразованного уравнения
равен примерно Л(<р~). В оценках (4.32Н4.34) можно считать &• ""
"" Л(<р~) и С "" 1. Для того чтобы сделать окончательные выводы, оста­
ется оценить Л(<р~).
Пусть 1• и ([' )• - приближенные значения функций f и f', вычис­
ляемые в малой окрестности корня х .Будем считать, что производная
f' вычисляется хотя бы с точностью до одной-двух верных значащих
цифр. В противном случае (особенно, если неверно определяется знак
f' ) из геометрического смысла метода легко понять, что его применять
не следует. В силу предложения 2.5 в малой окрестности корня имеем
л (L) ""лсr·) + Л<сr·)·) 111 "" лсr·) = &.
cr·)· 11'1 I!'12 lf'(x)1
Так как <р~(х) =х 9 /·~х) ""х то, учитывая погрешность, прибли-
(f') (х)
женно равную 1х1 Ем, вносимую в <р~ вследствие выполнения опера-
ции вычитания, получаем &N = Л(<р~) "" &+ 1х1 Ем.
Таким образом, преобразование уравнения f(x) = О к виду (4.45)
практически не меняет обусловленность и радиус & интервала неопре­
деленности корня х . Итерационный процесс Ньютона дает возмож­
ность вычислить решение с точностью i: ~ &. Отметим, тем не менее,
что эти достоинства метода Ньютона реализуются, вообще говоря,
только в малой окрестности корня.
§ 4.7. Модификации метода Ньютона
В § 4.6 в качестве недостатка метода Ньютона была отмечена необ­
ходимость вычисления значения производной f (х) на каждой итера­
ции. Рассмотрим некоторые модификации метода Ньютона, свободные
от этого недостатка. Заметим, что, по существу, излагаемые в этом
параграфе итерационные методы решения нелинейного уравнения на
каждой итерации используют некоторую процедуру его линеаризации,
118

120. § 4.7. Модификации метода Ньютона
т.е. исходное нелинейное уравнение заменяется приближенно более
простым линейным уравнением.
l. Упрощенный метод Ньютона. Если производная f'(x) непре­
рывна, то ее значение вблизи простого корня х почти постоянно.
Поэтому можно попытаться вычислить/' лишь однажды в точке х<0>, а
затем заменить в формуле (4.37) значение f' (х<п>) постоянной f'(x<0>). В
результате получим расчетную формулу упрощенного метода Ньютона:
х<п + 1) = х<п> - f(х<п>) ' п ~о. (4.46)
f'(x(O))
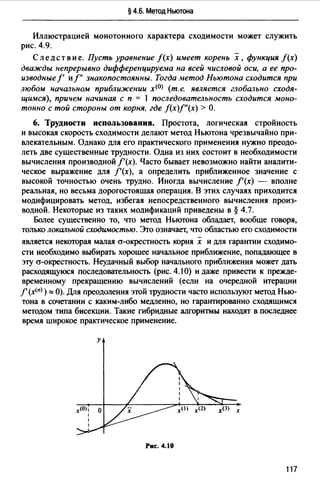
Геометрическая иллюстрация метода приведена на рис. 4.11. В точке
(x<OJ, f(x<O>)) к графику функции у = f(x) проводится касательная /0 и за
приближение xm принимается абсцисса точки пересечения этой каса­
тельной с осью Ох (как в методе Ньютона). Каждое следующее прибли­
жениех<п + 1>получается здесь как абсцисса точки пересечения с осью Ох
прямой, проходящей через точку М(п> с координатами (х<п>, f(х<п> )) и
параллельной касательной /0 •
Упрощение вычислений по сравнению с методом Ньютона достига­
ется здесь ценой резкого падения скорости сходимости. Сходимость
этого метода является уже не квадратичной, а линейной.
Метод (4.46) можно рассматривать как метод простой итерации
с итерационной функцией <р(х) =х - f(x<~> . Так как <р'(х) = 1 - f'(<x]>),
J'(x ) f'(x
то для знаменателя q соответствующей геометрической прогрессии
имеем q "' l 1 - ;~~~~)1 · Следовательно, скорость сходимости тем выше,
чем ближе начальное приближение х<0> к решению х .
у
о х
Рие. 4.11
119

121. Глава 4. Методы отыскания решений нелинейных уравнений
2. Метод ложного положениJ1. В основе этой и следующих двух
модификаций метода Ньютона лежит приближенное равенство
f'(x<n>) ,,,f(z<п>)-f(x(n)) .
z(n) -х<п)
(4.47)
Оно верно при условии z(n) "'х<п> и следует из определения производной:
f'(x) = lim f(z)-f(x).
z-x z-x
Пусть с - фиксированная точка, расположенная в окрестности про­
стого корня х. Заменим в расчетной формуле метода Ньютона (4.37)
производную f'(x<n>) правой частью приближенного равенства (4.47),
полагая z(n) = с. В результате придем к расчетной формуле метода
ложного положения:
с -х<п>
х<п + 1) =х(п) - J(х<п>) п 2 О.
f(c)-f(x<n>) '
(4.48)
Геометрическая иллюстрация метода приведена на рис. 4.12. Очеред­
ное приближение x(n + I) получается здесь как абсцисса точки пересече­
ния с осью Ох прямой, проведенной через расположенные на графике
функции у= f(x) точки ми мп> с координатами (с, f(c)) и (х<п>, лх<п>)).
Метод (4.48) обладает только линейной сходимостью. Его можно рас­
сматривать как метод простой итерации с итерационной функцией
<р(х)= х- ( ;-х( /(х). Так как скорость сходимости определяется
f с -f х
у
Рис. 4.12
120

122. § 4.7. Модификации метода Ньютона
вблизи корня величиной q ~ lчi'(x)I = l•-j(~)x2~~~11 ·то она тем
выше, чем ближе окажется выбранная точка с к х .
3. Метод секущих. Замена в формуле метода Ньютона производной
f(х<п-1 >)-!(x<n>)
f'(х<п>) приближением · приводит к расчетной формуле
х<п-1) _х(п)
метода секущих:
x<n-1) _x(n)
х<п + i >=х<п> - J(х<п>) п ;:: О.
!(х<п - 1>) _!(x<n>) '
(4.49)
Заметим, что этот метод двухшаrовый, так как для нахождения оче­
редного приближения х<п + I) требуется знание двух предыдущих при­
ближений х<п> и х<11 - 1). В частности, для того чтобы начать вычисления,
необходимо задать два начальных приближения х<0> и x(l>. Все рассмот­
ренные ранее методы требовали для вычисления х<п + 1) только знание
х<п>, т.е. были одношаrовыми.
На рис. 4.13 приведена геометрическая иллюстрация метода. Оче­
редное приближение х<п + I) получается здесь как абсцисса точки пере­
сечения с осью Ох секущей, соединяющей точки м<п - 1> и м<п> графика
функции f(x) с координатами (х<п - 1), f(х(п - 1))) и (х<11>, f(х<п>)).
Примечательно то, что эта модификация метода Ньютона сохраняет
свойство сверхлинейной сходимости, если вычисляется простой корень
х .Точнее, верно следующее утверждение.
м<О>
у
о
Рис. 4.13
121

123. Глава 4. Методы отыскания решений нелинейных уравнений
Теорема 4.9. Пусть х - простой корень уравнения f(x) =О, в
некоторой окрестности которого функция f дважды непрерывно диф­
ференцируема, 11ричем f"(x) ~ О. Тогда существует а-окрестность
корня х такая, что при произвольном выборе приближений х<0> и хО) из
.f5+ 1
этой а-окрестности метод секущих сходится с порядком р = 2 :::::
::::: 1.618, т.е для п ~ 1 справедлива оценка
J5 + 1
р =--.2 .
Так как одна итерация метода секущих требует только одного
нового вычисления значения функции f, а метод Ньютона - двух
вычислений значений функций (j и/'), то трудоемкость двух итера­
ций метода секущих приблизительно эквивалентна трудоемкости
одной итерации по Ньютону. Две итерации метода секущих дают
порядок р2 ::::: 2.618 > 2, поэтому его можно расценивать как более
быстрый по сравнению с методом Ньютона.
К сожалению, метод обладает, вообще говоря, только локальной схо­
димостью. Он требует выбора двух близких к х (в общем случае -
очень близких) начальных приближений x<OJ и xOJ. Если эти приближе­
ния выбраны неудачно, то метод расходится (рис. 4.14).
у
х
Рис. 4.14
4. Метод Стеффенеена. Итерационная формула метода Стеффен­
сена имеет вид
f(x<n>)
х<п+)=х<п)_ f(x<n>) п~О.
J(х<п) + J(x<n>))- J(x<n>) '
(4.50)
122

124. § 4.7. Модификации метода Ньютона
у
о х
Рис. 4.15
Можно считать, что она получена в результате замены производной
f'(х<п>), входящей в расчетную формулу метода Ньютона, приближе­
нием (4.47), где z(n) =х<п> + j(х<п>).
Метод Стеффенсена интересен тем, что он является одношаговым,
не требует вычисления производной f' и в то же время, как и метод
Ньютона, сходится квадратично, если корень х - простой, функция f
дважды непрерывно дифференцируема в окрестности корня, а началь­
ное приближение х<0> выбрано близко к х .
Геометрическая иллюстрация метода Стеффенсена приведена на
рис. 4.15. Приближение х<п + 1> получается как абсцисса точки пересе­
чения с осью Ох секущей, проходящей через точки м<п> и №n> с коор­
динатами (x<n), j(x<n>)) и (z<п>, f(z<n>)). Значение z(n) отвечает абсциссе
точки пересечения с осью Ох прямой у =j(х<п>) - (х - х<п>), проходящей
через точку м<п) и параллельной прямой у = -х.
Несмотря на свойство квадратичной сходимости, метод Стеффен­
сена уступает методу секущих, поскольку требует большей вычисли­
тельной работы для достижения той же точности Е. Это связано с тем,
что на каждой итерации рассматриваемого метода вычисление функции
производится дважды, а в методе секущих лишь один раз.
5. Уточнение метода Ньютона для случая кратного корня.
В принципе для вычисления корня уравнения f(x) = О кратности т > 1
можно использовать и стандартный метод Ньютона. Однако в этом слу­
чае скорость его сходимости является только линейной. Можно пока­
зать, что знаменатель q соответствующей геометрической прогрессии
приближенно равен 1 - 1/т.
123

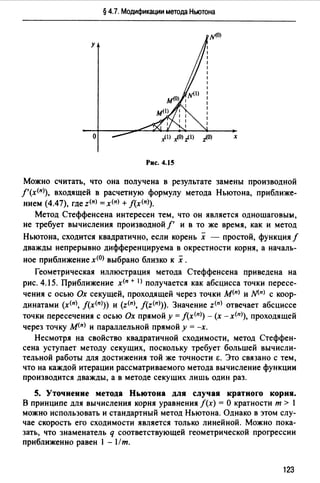
125. Глава 4. Методы отыскания решений нелинейных уравнений
у у
о х х о х х
Рис. 4.16
Для того чтобы сохранить квадратичную скорость сходимости,
метод Ньютона нужно модифицировать следующим образом:
f(x<n))
х<п+l)=х<п>-т--- п~О.
f'(х<п))'
(4.51)
Можно показать (это достигается раскрытием неопределенностей
с помощью формулы Тейлора), что при таком выборе итерационной
функции q>(x) = х - т f((x)) получим q>'(x) =О, и сходимость снова ока­
/' х
жется квадратичной.
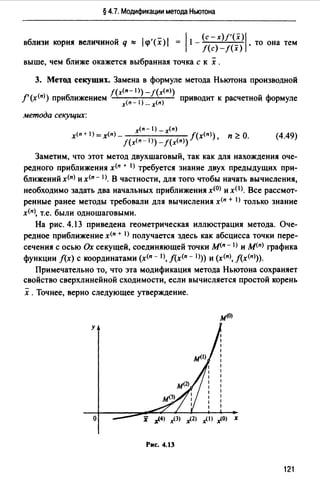
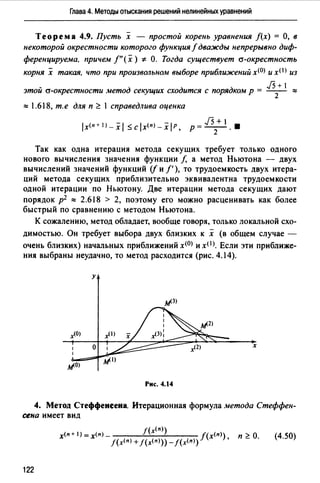
На рис. 4.16, а, б проиллюстрировано поведение последовательных
приближений стандартного метода Ньютона и его модификации (4.51)
для случая отыскания корня кратности т = 2.
Для метода (4.51) значение х<п + I) получается следующим образом.
В точке м<п) с координатами (х<п>, j(х<п>)) к графику функции прово­
дится касательная. Пересечение ее с осью Ох дает вспомогательную
точку :Х<п+ I). Для получения точки х<п + I) нужно воспользоваться
равенством х<п + 1J - х<п) = т( х (п + 1) - x<n>).
Пр им ер 4.10. Применим методы, рассмотренные в данной главе,
для вычисления положительного корня уравнения 4(1 - х2) - еХ = О, счи­
тая известным, что х Е [О, 1] (см. пример 4.2).
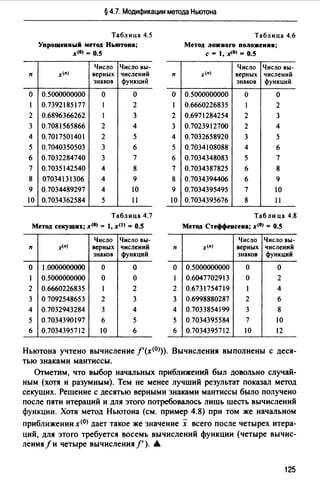
Результаты вычислений приведены в табл. 4.5-4.8. В них для каж­
дого приближения дается число верных знаков и требуемое число вычис­
лений значений функции /(х) = 4(1 - х2 ) - еХ (для упрощенного метода
124

126. § 4.7. Модификации метода Ньютона
п
о
1
2
3
4
5
6
7
8
9
10
Таблица 4.5
Упрощенный метод Ньютона;
х(О) = 0.5
Число Число вы-
x<•J верных числений
знаков функций
0.5000000000 о о
0.7392185177 1 2
0.6896366262 1 3
0.7081565866 2 4
0.7017501401 2 5
0.7040350503 3 6
0.7032284740 3 7
0.7035142540 4 8
07034131306 4 9
0.7034489297 4 10
О.7034362584 5 11
Таблица 4.7
Метод секущн:1; х<01 = 1, x<I) = 0.5
Число Число вы-
п х(•) верных числений
знаков функций
о 1.0000000000 о о
1 0.5000000000 о о
2 0.6660226835 1 2
3 о 7092548653 2 3
4 0.7032943284 3 4
5 0.7034390197 6 5
6 0.7034395712 10 6
п
о
1
2
3
4
5
6
7
8
9
10
п
о
1
2
3
4
5
6
Таблица 4.6
Метод ложноrо положено;
С = 1, х(О) = 0.5
Число Число вы-
x<•I верных числений
знаков функций
0.5000000000 о о
0.6660226835 1 2
0.6971284254 2 3
0.7023912700 2 4
0.7032658920 3 5
О. 7034108088 4 6
0.7034348083 5 7
0.7034387825 6 8
0.7034394406 6 9
0.7034395495 7 10
0.7034395676 8 11
Таблица 4.8
Метод Стеффенсена; х<81 = 0.5
Число Число вы-
x<•J верных числений
знаков функций
0.5000000000 о о
0.6047702913 о 2
0.6731754719 1 4
0.6998880287 2 6
0.7033854199 3 8
0.7034395584 7 10
О. 7034395712 10 12
Ньютона учтено вычисление /'(x<0J)). Вычисления выполнены с деся­
тью знаками мантиссы.
Огметим, что выбор начальных приближений был довольно случай­
ным (хотя и разумным). Тем не менее лучший результат показал метод
секущих. Решение с десятью верными знаками мантиссы было получено
после пяти итераций и для этого потребовалось лишь шесть вычислений
функции. Хотя метод Ньютона (см. пример 4.8) при том же начальном
приближении х<0> дает такое же значение х всего после четырех итера­
ций, для этого требуется восемь вычислений функции (четыре вычис­
ления f и четыре вычисления/'). А
125

127. Глава 4. Методы отыскания решений нелинейных уравнений
Таблица 4.9 Таблица 4.10
Метод Ньютона Уточнение метода Ньютона
х<п)
для случая т = 2
п
о 1.0000000000
п
_x(n)
0.6666666667 о 1.0000000000
2 0.4166666667 0.3333333333
3 0.2442528736 2 0.0476190476
4 0.1354180464 3 0.0011074197
5 0.0720028071 4 0.0000006128
6 0.0372524647 5 0.0000000000
7 о. о 189668249
8 0.0095725027
Пример 4.11. Применим метод Ньютона и его модификацию (4.51)
для вычисления корня х =О кратности т = 2 для уравнения х 2 еХ = О.
Возьмем х<0> = 1. Результаты вычислений даны в табл. 4.9 и 4.1 О.
Как видно из табл. 4.9, погрешность метода Ньютона убывает довольно
медленно и примерно соответствует геометрической прогрессии со знаме­
нагелем q = 112. В то же время пять итераций по формуле (4.51) при т = 2
дают значение решения с погрешностью, меньшей Е = 10-10. .А
6. Чувствительность к погрешностям. Рассмотренные в этом пара­
графе одношаговые методы можно интерпретировать как различные
варианты метода простой итерации. Поэтому исследование их чувстви­
тельности к погрешностям сводится (аналогично тому, как это было сде­
лано в § 4.6 для метода Ньютона) к использованию соответствующих
результатов § 4.5. Например, можно убедиться в хорошей обусловленно­
сти модифицированного метода Ньютона и метода ложного положения.
Высокая скорость сходимости метода секущих делает его привлека­
тельным для применения. Однако вызывает беспокойство тот факт, что
f(х<п - 1>) - f(x<n>)
в формулу (4.49) входит величина х<п- 1) _ х<п) , аппроксимирующая
производную. Вблизи корня, когда х<п) ::::: х<п - I) и J(x<n>) ::::: f(х<п - 1)) ::::: О,
погрешность вычисления функции начинает существенно сказываться
на точности этой величины, и метод секущих теряет устойчивость.
Этим он существенно отличается от методов простой итерации и Нью­
тона, для которых приближения x<n) равномерно устойчивы к погреш­
ности независимо от числа итераций п.
Тем не менее при грамотном использовании метод секущих дает
возможность получить почти столько же верных значащих цифр корня
х, сколько вообще позволяет обусловленность задачи (см. § 4.2). Воз-
126

128. § 4.8. Дополнительные замечания
можная (но не обязательная) потеря точности составляет одну-две вер­
ные цифры. Необходимо лишь прервать итерационный процесс в тот
момент, когда приближения окажутся в опасной близости к интервалу
неопределенности. Один из способов заметить этот момент состоит
в использовании правила Гарвика (см. § 4.2).
Отметим, что при попадании очередного приближения в малую
окрестность решения теряет устойчивость и метод Стеффенсена.
§ 4.8. Допопнитепьные замечани1
1. Метод обратной квадратичной интерполяции. Пусть приближе­
ния х<п - 2), х<п - 1>, х<п) уже найдены, а соответствующие значения функ­
ции f различны (последнее предположение заведомо будет выполнено,
если функция/строго монотонна). Тогда строят такой квадратичный мно­
гочлен Р2(у) от переменной у, что х<1) = P 2(f(x(r))) для i = п - 2, п - 1, п.
За очередное приближение к решению принимается х<п + I) =Р2(0).
Этот трехшаrовый метод обладает локальной сходимостью с поряд­
ком р "" 1.839; для начала ero работы требуется задание трех хороших
начальных приближений.
2. Методы с порядком сходимости выше второrо. Приведем при­
меры одношаrовых методов, обладающих кубической сходимостью.
Таковым является итерационный метод1
Здесь
_ /(х)
и(х)- f'(x)'
v (х) =f(x)f"(x).
[f '(х)]2
Другим примером метода, обладающего кубической скоростью схо­
димости, является метод Галлея2
1 Этод метод часто называют итерационным методом Эйлера.
2 Эдмунд Галлей (1656-1742) - анrлнйскнй астроном, предсказавший периодиче­
ское (с периодом 75 лет) появление кометы, впоследствии названной ero именем.
127

129. Глава 4. Методы отыскания решений нелинейных уравнений
Существуют и другие методы с порядком сходимости выше второго,
теоретически очень быстро сходящиеся вблизи корня. Однако они
редко используются на практике, так как их преимущество в скорости
сходимости начинает проявляться лишь тогда, когда итерации уже
почти сошлись и в действительности осталось сделать одну-две итера­
ции либо вообще пора прекратить вычисления. Чтобы ощутить преиму­
щество таких методов над методами Ньютона и секущих, нужны ком­
пьютер с очень высокой разрядностью и желание получить решение с
чрезвычайно высокой точностью.
3. Вычисление корней многочленов. Вычисление корней много­
членов Рm(x) степени т - специальная задача, для решения которой раз-
работано большое число эффективных алгоритмов. Укажем на один из
них - метод Мюллера. В нем по трем ранее найденным приближениям
х<п - 2), х<п - 1>, х(п) строят интерполяционный многочлен второй степени
Q2 (х), т.е. такой многочлен, для которого Q2 (x(l)) = Рт(хИ) при 1 = п - 2,
п - 1, п. За очередное приближение х<п + 1> принимают тот из двух кор­
ней многочлена Q2 (х) (в общем случае являющихся комплексными),
который расположен ближе к х<п>. Метод Мюллера сходится с поряд­
ком р "" 1.839.
3 а меч ан и е. Метод Мюллера считается также эффективным
методом отыскания комплексных корней функций комплексной
переменной.
Вплоть до начала 60-х годов ХХ в. задача отыскания корней много­
членов была весьма распространенной. Одна из основных причин
состояла в том, что к отысканию корней характеристического много­
члена сводилась одна из важнейших задач алгебры - задача вычисле­
ния собственных чисел матриц. В настоящее время существуют другие,
гораздо более эффективные методы вычисления собственных значений
(см. гл. 8), и, по-видимому, задача вычисления корней многочлена во
многом потеряла свою актуальность.
Как было отмечено ранее, к задаче отыскания корней многочлена
высокой степени с приближенно заданными коэффициентами следует
отнестись очень осторожно. она может оказаться плохо обусловленной
(см. в гл. 3 пример Уилкинсона). Вообше, можно посоветовать избегать
применения методов решения вычислительных задач, в которых
используются многочлены высокой степени.
4. Гибридные алгоритмы. В последние годы получили признание
алгоритмы, которые называют гибридными (или регуляризованны,wи).
Они представляют собой комбинации надежных, но медленно сходя-
128

130. § 4.8. Дополнительные замечания
щихся методов типа бисекции с недостаточно надежными, но быстро
сходящимися методами типа секущих или Ньютона. Результирующие
алгоритмы обладают высокой надежностью и гарантированной сходимо­
стью. В тех же случаях, когда в окрестности простого корня функция/­
гладкая, сходимость становится сверхлинейной.
Алгоритм ZEROIN, изложенный в [106], является примером эффек­
тивного гибридного алгоритма. на каждом шаге которого принимается
решение о том, какой из трех методов: бисекции, секущих или обрат­
ной квадратичной интерполяции - следует использовать для вычисле­
ния очередного приближения.
5. Л2-процесс Эйткена. Пусть {х<п>},~0 - последовательность
приближений к корню х ,полученная линейно сходящимся итерацион­
ным методом (например, методом простой итерации). Использовав три
последние найденные приближения х<п - 1), х<п>, х<п + 1>, можно получить
более точное приближение к решению
_ (х<п + 1) _ х<п))2
х<п + 1) =х<п + J) _ -~----~-­
t'(n + 1) _ 2х<п) + х<п - 1) ·
Этот способ ускорения сходимости используется на завершающем
этапе итераций и называется Л2-процессом Эйткена.
6. Критерии окончания. Проблема выбора правильного критерия
окончания итерационного процесса часто оказывается достаточно
сложной. Следует также иметь в виду, что наряду с обсуждавшимся в
предыдущих параграфах условием /х<п>-х<п- I) 1 < Е 1 нередко исполь-
зуется следующее условие: /J(х<п>)/ < Е2.
129

131. Глава 5
ПРЯМЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 5. 1. Постановка задачи
В вычислительной линейной алгебре традиционно выделяют четыре
основные задачи:
1) решение систем линейных алгебраических уравнений;
2) вычисление определителей;
3) нахождение обратных матриц;
4) определение собственных значений и собственных векторов.
В последние десятилетия к первым четырем задачам добавились
еще две:
5) линейная задача метода наименьших квадратов;
6) вычисление сингулярных чисел и сингулярных векторов.
Задачи 2 и 3 обсуждаются в § 5.6, последней по порядку (но не по зна­
чению) задаче 4 посвящена гл. 8. Задачи 5 и 6 рассматриваются в§ 5.12.
В основном же данная глава посвящена задаче 1, а более точно -
прямым методам решения систем линейных алгебраических уравнений
с вещественными коэффициентами:
0 11 х 1 + о 12х2 + о 13х3 + ... + о 1 тхт = Ь 1 ,
021 х, + О22Х2 + О23Х3 + ... + О2тхт = Ь2,
аз1Х1 + О32Х2 + аз3Х3 + ... + О3тхт = Ь3, (5.l)
ОтХ + атr2 + От3Х3 + ··· + От~т = Ьт.
В матричной форме записи эта система принимает вид
где
130
А=
0 11 а 12 0 13
а2 а22 а23
О31 О32 О33
Ах=Ь, (5.2)
, х=

132. § 5.2. Нормы вектора и матрицы
Итерационные методы решения системы (5.1) будут рассмотрены в rn. 6.
Уделим основное внимание задаче вычисление вектора х, являюще­
гося решением системы (5.2), по входному данному - вектору Ь. Будем
предполагать, что матрица А задана и является невырожденной.
Известно, что в этом случае решение системы существует, единственно
и устойчиво по входным данным. Это означает, что рассматриваеfая
задача корректна.
Хотя задача решения системы (5.1) сравнительно редко представ­
ляет самостоятельный интерес для приложений, от умения эффективно
решать такие системы часто зависит сама возможность математиче­
ского моделирования самых разнообразных процессов с применением
компьютера. Как будет видно из дальнейшего изложения, значительная
часть численных методов решения различных (в особенности - нели­
нейных) задач включает в себя решение систем (5.1) как элементарный
шаг соответствующего алгоритма.
Пустьх* = (х;,х;, ...,x:)r - приближенное решение системы (5.1).
В этой и следующих главах мы будем стремиться к получению реше­
ния, для которого погрешность е = х - х• мала (количественные
характеристики «величины» погрешности будут введены в следую­
щем параграфе). Тем не менее заметим, что качество полученного реше­
ния далеко не всегда характеризуется тем, насколько мала погрешность
х - х*. Иногда вполне удовлетворительным является критерий малости
невязки r = Ь - Ах*. Вектор r показывает, насколько отличается правая
часть системы от левой, если подставить в нее приближенное решение.
Заметим, что r =Ах - Ах*= А(х - х*) и поэтому погрешность и невязка
связаны равенством
е=х-х* =A- 1r. (5.3)
§ 5.2. Нормы вектора и матрицы
1. Норма вектора. Решением системы линейных алгебраических
уравнений является вектор х = (х 1 , х2, ... , хт)т, который будем рассматри­
вать как элемент векторного пространства вт. Приближенное решение
х* = (х;,х;, ..., x:)r и погрешность е = х - х* = (х 1 - х;, ..., хт - х: )Т
также являются элементами пространства Rт. Для того чтобы анализи­
ровать методы решения систем, необходимо уметь количественно оце­
нивать «величины» векторов х· их - х•, а также векторов Ь и Ь - ь•, где
ь· = сь;, ь;, ...,ь:)т - вектор приближенно заданных правых частей.
Удобной для этой цели количественной характеристикой является
широко используемое понятие нормы вектора.
131

133. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Говорят, что в ят задана норма, если каждому вектору х из Rm
сопоставлено вещественное число llxl , называемое нормой вектора х
и обладающее следующими свойствами:
1) lxll ~ О, причем lxll = О тогда и только тогда, когда х = О;
2) llaxll = lal llxll для любого векторах и любого числа а;
3) llx +yll $ llxll + lyll для любых векторов х и у;
последнее неравенство принято называть неравенством треугольника.
Заметим, что такими же свойствами обладает обычная геометриче­
ская длина вектора в трехмерном пространстве. Свойство 3) в этом слу­
чае следует из правила сложения векторов и из того известного факта,
что сумма длин двух сторон треугольника всегда больше длины третьей
стороны.
Существует множество различных способов введения норм. В
вычислительных методах наиболее употребительными являются сле­
дующие три нормы:
т
llxll1=rlx1I. lxl00 = max lx"I .
l<;i<;m
(5.4)
i= 1
Первые две из них являются частными случаями более общей нормы:
р ~ 1 (5.5)
(при р = 1 и р = 2), а последняя, как можно показать, получается из
нормы (5.5) предельным переходом при р --+ оо.
Замечание 1. Норма llxll2 = lxl является естественным обоб­
щением на случай т-мерного пространства понятия длины вектора
в двух- и трехмерных геометрических пространствах. Поэтому ее
называют евклидовой нормой или модулем векторах.
Замечание 2. Справедливы неравенства
llxllоо $ llxll2 $ llxll 1 $ т llxll оо , (5.6)
указывающие на то, что в определенном смысле все три введенные
нормы эквивалентны: каждая из них оценивается любой из двух
других норм с точностью до множителя, зависящего от т.
Пр и мер 5.1. Найдем llxll 1 , llxll2 , llxll 00 для вектора х
= (0.12, -0.15, 0.16)~
132

134. § 5.2. Нормы вектора и матрицы
По формулам (5.4) определяем llxll 1 = 0.12 + 0.15 + 0.16 = 0.43, llxll2 =
=(О.12 2 +0.152+0.16 2 )112 =0.25, llxll00 =max{0.12,0.15,0.16} =О.16. А
2. Скалярное произведение. Напомним, что скалярным произве­
дением векторов х = (х1 , х2, "., хт)т и у= (у1 , у2, "., Ут)Т называется
величина
т
(х,у)=х1У1 +х2у2+ ". +хтут= LX1Y1·
i=
Нетрудно заметить, что llxll2 = (х, х) 112 •
(5.7)
Когда векторы х, у имеют комплексные компоненты, скалярное про­
изведение понимают так:
т
(х, У)= Х1У1 + Х2У2 + ". + ХтУт = LX1Y1 ·
/=
3. Абсолютная и относительная погрешности вектора. Далее
будем всюду считать, что в пространстве т-мерных векторов Rm вве­
дена и фиксирована некоторая норма llxll (например, одна из норм
llx!IP, l s р s оо). В этом случае в качестве меры степени близости век-
торов х и х• естественно использовать величину llx - х* 11 , являющуюся
аналогом расстояния между точками х и х•. Введем абсолютную и
относительную погрешности вектора х• с помощью формул
• ll *ll " • llx - х*11
Л(х) = х-х , u(x) = -llx-ll-. (5.8)
Выбор той или иной конкретной нормы в практических задачах дик­
туется тем, какие требования предъявляются к точности решения. Выбор
нормы llxll 1 фактически отвечает случаю, когда малой должна быть сум-
марная абсолютная погрешность в компонентах решения; выбор llxll2
соответствует критерию малости среднеквадратичной погрешности, а
принятие в качестве нормы llxll= означает, что малой должна быть мак­
симальная из абсолютных погрешностей в компонентах решения.
4. Сходимость по норме. Пусть {x<nJ}~ 1 - последовательность
векторов x<nJ = (xn>, х~п), ..., х~){. Говорят, что последовательность
векторов x<nJ сходится к вектору х при п --> оо (x(n) --> х при п --> оо),
если Л(х<пJ) = llx<nJ_xll -->О при п--> оо.
133

135. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Замечание. Сам факт наличия или отсутствия сходимости х<п)
к х при п -+ оо в конечномерных пространствах не зависит от
выбора нормы. Известно, что из сходимости последовательности
по одной из норм следует сходимость этой последовательности по
любой другой норме. Например, для норм llxll 1, llxll2 , llxll00 это
вытекает из неравенств (5.6). Более того, х<п) -+ х при п -+ оо
тогда и только тогда, когда для всех i = 1, 2, ..., т имеем х~п) ---+ Х;
при п---+ оо, т.е. сходимость по норме в вт эквивалентна покомпо­
нентной (покоординатной) сходимости.
S. Норма матрицы. Величина
llAxll
llAll =r;i~~ Тхf (5.9)
называется нормой матрицы А, подчиненной норме векторов, введен­
ной в вт.
Заметим, что множество всех квадратных матриц размера т х т
является векторным пространством. Можно показать, что введенная
в этом пространстве формулой (5.9) норма обладает следующими свой­
ствами, аналогичными свойствам нормы вектора:
1) llA11 ~ О, причем llA 11 = О тогда и только тогда, когда А = О;
2) llaAll = lal llAll для любой матрицы А и любого числа а;
3) llA + Bll s llAll + llBll для любых матриц А и В.
Дополнительно к этому верны следующие свойства:
4) llA ·Bll s llAll · llBll для любых матриц А и В;
5) для любой матрицы А и любого векторах справедливо неравенство
llAxll s llAll · llxll. (5.10)
Докажем, например, свойство 5). Если llxll ~О, то неравенство (5.10)
эквивалентно неравенству llAxll / llxll s llA11 , справедливость которого
следует из определения (5.9). Если же llxll =О, то неравенство (5.10)
превращается в верное числовое неравенство О s О.
Как следует из определения (5.9), каждой из векторных норм llxll
соответствует своя подчиненная норма матрицы А. Известно, в частно­
сти, что нормам llxll 1, llxll2 и llxll00 подчинены нормы llAll 1, llAll2
и llA1100 , вычисляемые по формулам
т
llAll 1 = ~~; L laijl,
J _;_m i=I
(5.11)
llAll2 = max J'Л.iATA),
1 SjSm
(5.12)
134

136. § 5.2. Нормы вектора и матрицы
где Л}АТА) - собственные числа 1 матрицы АТА;
т
IJAlloo = max L la;;I. (5.13)
1 $ {$ т ]= 1 .
Нормы llAll 1 и llAll 00 вычисляются просто (см. ниже пример 5.2).
Для получения значения первой из них нужно найти сумму модулей эле­
ментов каждого из столбцов матрицы А, а затем выбрать максимальную
из этих сумм. Для получения значения llAll00 нужно аналогичным
образом поступить со строками матрицы А.
Как правило, вычислить значение нормы llAll2 бывает трудно, так
как для этого следует искать собственные числа Л1. Для оценки вели­
чины llAll2 можно, например, использовать неравенство
(5.14)
Здесь llAllE= J,,~I laul 2- величина, называемая евклидовой нормой
матрицы А. Часто эту же величину называют нормой Фробениуса 2 и
обозначают llA 11F.
Норма (5.9) имеет простую геометрическую интерпретацию. Для того
чтобы ее привести, заметим, что операцию умножения матрицы А на век­
тор х можно рассматривать как преобразование, которое переводит вектор
х в новый вектор у = Ах. Если значение llxll интерпретируется как длина
векторах, то величина llAxll / llxll есть коэффициент растяжения векторах
под действием матрицы А. Таким образом, величина
llAxiJ
kmax = llA11 = ~:~ bl (5.15)
представляет собой максимальный коэффициент растяжения векторов
под действием матрицы А. Полезно отметить, что для невырожденной
матрицы А минимальный коэффициент растяжения kmin отвечает норме
обратной матрицы и вычисляется по формуле
k - 11л-111-1 - . llAxll
mln - - ~~~ Тхf · (5.16)
Заметим, что в случае llA 11 < 1 происходит сжатие векторов под дей­
ствием матрицы А.
1 Напомним, что число Л. называется собственным числом матрицы А, если существует
вектор х ~ О такой, что Ах= J..x. Каждая матрица порядка т имеет ровно т собственных
чисел (вообще говоря, комплексных) с учетом их кратности.
~ Фробениус Фердинанд Георг (1849-1917) - не'lецкий математик.
135

137. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Пр и мер 5.2. Для матрицы
r
O.I -0.4 О ]
А= 0.2 О -0.3
о 0.1 0.3
найдем llA11 1 , llA 11 оо и оценим llA112 •
В соответствии с формулами (5.11), (5.13) и неравенством (5.14) имеем
llAll 1 = max{O.I + 0.2 +О; 0.4 +О+ 0.1; О+ 0.3 + 0.3} = 0.6;
llAll00 = max{O.I + 0.4 +О; 0.2 +О+ 0.3; О+ 0.1+0.3} = 0.5;
§ 5.3. Типы используемых матриц
Эффективность вычислений в линейной алгебре существенно зави­
сит от умения использовать специальную структуру и свойства исполь­
зуемых в расчетах матриц. Напомним некоторые важные типы матриц.
Квадратная матрица А называется диагональной, если ее элементы
удовлетворяют условию а11 = О для i "# j (все отличные от нуля элементы
расположены на главной диагонали):
а11 о о о
о а22 о о
А= о о а33 ." о
.................
О О О ... атт
Диагональную матрицу, у которой все элементы а11 главной диаго­
нали равны единице, называют единичной и обозначают буквой Е:
1 о о ". о
о 1 о ... о
Е= о о 1 ." о
. . . . . . . . . . . .
о о о ". 1
136

138. § 5.3.Типы используемых матриц
Пр им ер 5.3. Вычислим норму единичной матрицы Е.
llExll llxll
По определению, llEll = ~~~ ТхiГ =~~~ llxll = l . Следовательно,
llEll = 1. .А
Важную роль в численном анализе играют треугольные матрицы.
Квадратная матрица А называется нижней треугольной, если все ее
элементы, расположенные выше главной диагонали, равны нулю
(о11 = О для i < }). Если же равны нулю все элементы матрицы, распо-
ложенные ниже главной диагонали (o1j = О для i > }), то она называ­
ется верхней треугольной.
Нижняя и верхняя треугольная матрицы имеют соответственно сле­
дующий вид:
0 11 о о о 0 11 0 12 °13 0 1т
0 21 0 22 о о о 0 22 О23 02т
й31 О32 й33 о о о О33 03т
.. .. .. .......... . .................
0тt 0т2 °т3 •.. 0тт о о о ... 0тт
Треугольные матрицы обладают рядом замечательных свойств. Напри­
мер, для таких матриц определитель легко вычисляется по формуле
(5.17)
Квадратная матрица А называется симметричной, если она совпа­
дает со своей транспонированной матрицей Ат (или, что то же, oij = 011
для всех i,j).
Будем называть симметричную матрицу А положительно опреде­
ленной и писать А > О, если для всех векторов х ;tO квадратичная форма
т
(Ах, Х) = L Ol]XIXJ
i,]=I
принимает положительные значения.
Обозначим через Л.mtn и Л.mах минимальное и максимальное собст­
венные значения матрицы А. Известно, что для симметричной матрицы
Л.miпllxll; ~ (Ах,х) ~ Л.maxllxll;
и матрица А положительно определена тогда и только тогда, когда все
ее собственные значения положительны.
137

139. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Одна из трудностей практического решения систем большой размер­
ности связана с ограниченностью оперативной памяти компьютера Хотя
объем оперативной памяти вновь создаваемых вычислительных машин
растет очень быстро, тем не менее еще быстрее возрастают потребности
практики в решении задач все большей размерности (напомним, что для
хранения в оперативной памяти компьютера матрицы порядка т требу­
ется т2 машинных слов). В значительной степени ограничения на раз­
мерность решаемых систем можно снять, если использовать для хране­
ния матрицы внешние запоминающие устройства. Однако в этом случае
многократно возрастают как затраты машинного времени, так и слож­
ность соответствующих алгоритмов. Поэтому при создании вычисли­
тельных алгоритмов линейной алгебры большое внимание уделяют спо­
собам компактного размещения элементов матриц в памяти компьютера.
Заметим, что для хранения диагональной матрицы достаточно отвести
массив длины т и расположить в нем элементы а 11 , а22, "., атт· Для хра­
нения треугольной матрицы достаточно т(т + 1)/2 ячеек памяти, что
примерно вдвое меньше места, отводимого для хранения матрицы
общего вида. Столько же ячеек используется для хранения симметричной
матрицы, поскольку такая матрица полностью определяется, например,
заданием своей нижней треугольной части.
К счастью, приложения очень часто приводят к матрицам, в кото­
рых число ненулевых элементов много меньше общего числа элемен­
тов матрицы. Такие матрицы принято называть разреженными. Напро­
тив, матрицы общего вида называют плотными (или заполненными).
Разреженность матрицы является очень ценным свойством, поскольку
объем информации, который следует обрабатывать и хранить в памяти
компьютера, для таких матриц даже очень большого размера может
оказаться не слишком большим. Для хранения всех ненулевых элемен­
тов и информации об их расположении оказывается достаточным
использовать только оперативную память компьютера. Иногда эле­
менты матрицы известны либо вычисляются по простым формулам и
необходимость в их хранении отпадает.
Одним из основных источников разреженных матриц являются
математические модели технических устройств, состоящих из большого
числа элементов, связи между которыми локальны. Простейшие при­
меры таких устройств - сложные строительные конструкции и боль­
шие электрические цепи Другой важный источник разреженности -
метод конечных разностей и метод конечных элементов, используемые
для решения уравнений математической физики.
Известны примеры решенных в последние годы задач, где число
неизвестных достигало сотен тысяч Естественно, это было бы невоз­
можно, если бы соответствующие матрицы не являлись разреженными
(число элементов матрицы при т = 1os равно т х т = 1О 1 0).
138

140. § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений
Рис. 5.1
Простой пример разреженной матрицы дает трехдиагональная
матрица
all 0 12 о о о о о
0 21 0 22 0 23 о о о о
о О32 О33 034 о о о
о о о о ". 0т-1,т-2 0т-1,т-1 0т-1,т
о о о о о 0т,т-1 0тт
все ненулевые элементы которой расположены на главной и двух сосед­
них с ней диагоналях. Число этих элементов равно 3т - 2, что при боль­
шом т много меньше общего числа т2 элементов матрицы.
Многие приложения приводят к системам уравнений с так называе­
мыми ленточными матрицами. Матрица А называется ленточной с полу­
шириной ленты, равной /, если aij = О для 1i - j 1 > /. Все ненулевые эле­
менты такой матрицы расположены на s = 21 + 1 ближайших к главной
диагоналях матрицы; число s принято называть шириной ленты. Схема­
тически ленточная матрица представлена на рис. 5.1. Частным случаем
ленточной матрицы при s = 3 является трехдиагональная матрица. Ясно,
что в случае s « т ленточная матрица является разреженной.
§ 5.4. Обусловленность задачи реwени1 системы
линейных алгебраических уравнений
Оказывается, что решения различных систем линейных алгебраиче­
ских уравнений обладают разной чувствительностью к погрешностям
входных данных. Так же как и другие задачи (см. § 3.2), задача вычис­
ления решения х системы уравнений
Ах=Ь (5.18)
может быть как хорошо, так и плохо обусловленной.
139

141. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Исследование обусловленности задачи начнем со случая, когда эле­
менты матрицы А считаются заданными точно, а вектор-столбец пра­
вой части - приближенно.
Л ем м а 5.1. Для погрешности приближенного решения системы
(5.18) справедлива оценка
Л(х*) S llA-111 · llrll, (5.19)
где r = Ь -Ах* - невязка. отвечающая х*.
Для доказательства достаточно взять норму левой и правой частей
равенства (5.3) и воспользоваться свойством (5.1 О). 8
Теорема 5.1. Пусть х• - точное решение системы Ах*= ь•, в
которой правая часть ь• является приближением к Ь. Тогда верны сле­
дующие оценки абсолютной и относительной погрешностей:
Л(х*) S vлЛ(Ь*),
о(х°) s voo(b*),
(5.20)
(5.21)
где vл = 1/А-1 1/, v0(x) = 1/А-1 1/ • llbll/ l/xll = llA-111 • llAx/I / l/xll .
Доказательство. В рассматриваемом случае r = Ь-Ах* = Ь-Ь* и
неравенство (5.19) принимает вид (5.20). Разделив теперь обе части
неравенства (5.20) на l/xll и записав его в виде
л(х*) llл- 1 1/ • llьll л(ь*)
Тхf S l/xll lЬf'
приходим к оценке (5.21). 8
140
Замечание 1. Величина Vл = llA-111 для задачи (5.18) играет
роль абсолютного числа обусловленности (см. § 3.2).
Замечание 2. Величина v0(x) = llA-111 • llbll/llxll называется
естественным числом обусловленности. Она зависит от конкрет­
ного решения х и характеризует коэффициент возможного возрас­
тания относительной погрешности этого решения, вызванного по­
грешностью задания правой части. Это означает, что v0 (x) для за-
дачи вычисления решения х системы (5.18) играет роль относи­
тельного числа обусловленности (см. § 3.2).
Замечание 3. Полученные в теореме 5.1 оценки точны в том
смысле, что для системы Ах = Ь с произвольной невырожденной
матрицей А и любой заданной правой частью Ь 7- О найдется сколь
угодно близкий к Ь приближенно заданный вектор ь• 7- Ь, для кото­
рого неравенства (5.20) и (5.21) превращаются в равенства.

142. § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений
Вычислим максимальное значение естественного числа обусловлен­
ности, использовав определение (5.4) нормы матрицы:
llA-111 • llAxll
max v0(x) =max ll ll = llA-111 · llAll.
х~О х~О х
(5.22)
Полученную величину принято называть стандартным числом обу­
словленности (или просто числом обусловленности) матрицы А и обо­
значать через v(A) или сопd(А). Таким образом,
v(A) = сопd(А) = llA-111 • llA 11 . (5.23)
Сформулируем важное следствие из теоремы 5.1.
Следствие. В условиях теоремы 5.1 справедлива оценка
о(х*) :::::: cond(A) · о(Ь•). (5.24)
Для ее доказательства достаточно воспользоваться оценкой (5.21)
и заметить, что в силу равенства (5.22) верно неравенство v0 :::::: cond(A). 8
Замечание. Оценка (5.24) точна в том смысле, что для сис­
темы (5.18) с произвольной невырожденной матрицей А найдутся
правая часть Ь * О (и отвечающее этой правой части решение х)
и сколь угодно близкий к ь приближенно заданный вектор ь· * ь
такие, что неравенство (5.24) превращается в равенство.
Величина cond(A) является широко используемой количественной
мерой обусловленности системы Ах = Ь. В частности, систему и матрицу
А принято называть плохо обусловленными, если cond(A) » 1. В силу
оценки (5.24) и последнего замечания для такой системы существуют
решения, обладающие чрезвычайно высокой чувствительностью к
малым погрешностям задания входного данного Ь. Тем не менее заме­
тим, что не для всякого решения х коэффициент v0 (х) роста относи­
тельной погрешности достигает значений, близких к максимально воз­
можному значению cond(A).
Отметим следующие свойства числа обусловленности.
1°. Для единичной матрицы cond(E) = 1.
Доказательство. Пользуясь тем, что Е- 1 = Е и llEll = 1 (см. при-
мер 5.3), получаем cond(E) = llE-111 • llEll = 1. 8
2°. Справедливо неравенство cond(A) ~ .
Доказательство. Из равенства Е =А· А- 1 , свойства 4° норм мат-
риц и равенства llEll = 1 следует, что 1 = llEll:::::: llA-111 • llAll =cond(A). 8
3°. Число обусловленности матрицы А не меняется при умноже­
нии матрицы на произвольное число а * О.
141

143. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Доказательство. Заметим, что (а.А)-1 = а-1А- 1 . Поэтому
сопd(а.А) = llaAll · ll(aA)-111 = 1ai · l!All I aJ-1l!A-111 = сопd(А). 8
Замечание. Пользуясь приведенной в § 5.2 геометрической
интерпретацией норм матриц А и А- 1 (см. формулы (5.15) и (5.16)),
число обусловленности можно интерпретировать как отношение
максимального коэффициента растяжения векторов под действием
матрицы А к минимальному коэффициенту. сопd(А) = kmax/kmin·
Величина сопd(А) зависит, вообще говоря, от выбора нормы векто­
ров в пространстве Rm. Фактически это есть зависимость максимального
коэффициента роста погрешности от способа измерения величины вход­
ных данных и решения. В частности, выбору нормы llxllp (1 $ р $ оо)
отвечает сопdР(А) = l!A-1llP · llAllP.
Пр им ер 5.4. Вычислим сопd 00 (А) для матрицы
A=[l.03 0.991]·
0.991 0.943
Сначала найдем обратную матрицу
А-1 "'[-87.4 91.8 ] .
91.8 -95.4
(5.25)
Тогда сопd 00 (А) = llAll 00 • llA-111 00 "'2.о21·187.2 "'378. Если вход­
ные данные для системы уравнений с матрицей (5.25) содержат относи­
тельную погрешность порядка 0.1-1 %, то систему можно расценить
как плохо обусловленную. •
Пр им ер 5.5. Рассмотрим систему уравнений
1.03х 1 +0.99lx2 = 2.51,
(5.26)
О.991х 1 + О.943х2 = 2 41
с матрицей (5.25). Ее решением является х 1 "' 1 981, х2 "' 0.4735. Правая
часть системы известна в лучшем случае с точностью до 0.005, если
считать, что числа 2.51 и 2.41 получены округлением «истинных)) зна­
чений при вводе в память трехзначного десятичного компьютера. Как
влияет погрешность во входных данных такого уровня на погрешность
решения? Возмутим каждую из компонент вектора правой части Ь =
= (2 51, 2.4J)T на 0.005, взяв ь• = (2.505, 2.415)r. Решением системы,
142

144. § 5.4. Обусловленность задачи решения системы линейных алгебраических уравнений
отвечающим Ь*, является теперь х~ ::::: 2.877, х~ ::::: -0.4629. Таким обра­
зом, решение оказалось полностью искаженным. Относительная
погрешность задания правой части о(Ь*) = llb- b*ll оо / llbll00 =0.00512.51 :::::
::::: 0.2 % привела к относительной погрешности решения о(х*) =
= llx-x·llooillxll00 ::::: 0.9364/1.981 ::::: 47.3 %. Следовательно, погреш­
ность возросла примерно в 237 раз.
Можно ли внести в правую часть системы (5.26) такую погрешность,
чтобы получить существенно большее, чем 237, значение коэффициента
роста погрешности? Вычислим естественное число обусловленности,
являющееся максимальным значением рассматриваемого коэффициента,
отвечающим решению х ::::: (1.981, 0.4735)r и получим v0(x)
= llA-1lloollbll00 /llxll 00 ::::: 187.2 · 2.51/1.981 ::::: 237. Таким образом, на
поставленный вопрос следует ответить отрицательно.
Можно дать следующую геометрическую интерпретацию рассмот­
ренного примера. Каждому уравнению системы (5.26) соответствует
прямая на плоскости Ох 1х2. По коэффициентам при х 1 и х2 в этих урав­
нениях вндно, что прямые почти параллельны. Так как вблизи точки
пересечения прямые почти сливаются, то даже незначительная
погрешность в задании положения этих прямых существенно меняет
положение точки пересечения (рис. 5.2). •
Рис. 5.2
Пр им ер 5.6. Традиционным примером очень плохо обусловленной
матрицы является матрица Гильберта 1 -матрица Нс элементами hlJ =
= 1/(i + j - 1).
1 Давид Гильберт (1862-1943) - немецкий математик, исследования которого ока­
зали большое влияние на развитие современной математики.
143

145. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Таблица 5.1
Порядок матри- 2 3 4 5 6 7 8 9 10
цы Гильберта
Приближенное 2. 101 5. 102 2. 104 5 · 105 2. 107 5 · 108 2. 1010 5. 1011 2. JOIЗ
значение числа
обусловленности
Из табл. 5.1, заимствованной из (107), видно, что для матрицы Н даже
сравнительно невысокого порядка число обусловленности оказывается
чрезвычайно большим. .&
До сих пор мы предполагали, что матрица А задана точно. Однако
на практике это часто не так. Как выясняется, введенная выше вели­
чина cond(A) характеризует также и чувствительность решений сис­
темы к малым погрешностям задания элементов матрицы А. В подтвер­
ждение сказанного приведем следующий результат.
Теорема 5.2. Пусть х• - точное решение системы А.х• = Ь с
приближенно заданной матрицей А• . Тогда верна следующая оценка
относительной погрешности:
о• (х*) ~ cond(A) •о(А. ), (5.27)
где о*(х*} = llx-x•ll!llx*ll, о(А.) = /IA-A.ll/llAll.
Доказательство. В данном случае невязка r имеет вид r = Ь -Ах*=
=А.х• - Ах* =(А. - А)х*. Применяя неравенство (5.19), получаем
цепочку неравенств
• • _x-x*ll < A-11 • l(A.-A}x•ll < A-1l • IA.-A · x*
0 (х )-li711- llx*ll - llx*ll
=cond(A) • о(А. ). 8
Следствие. В условиях теоремы 5.2 справедливо приближенное
неравенство
144
о(х*) ~ cond(A) •о(А. ). (5.28)
Замечание 1. Когда с погрешностью заданы как правая часть
системы, так и матрица (т.е. х• является решением системы А.х• =
= Ь*), причем cond(A) •о(А.) « 1, можно доказать справедливость
неравенства
о(х*) ~ cond(A)(o(b*) + о(А. )).

146. § 5.5. Метод Гаусса
Замечание 2. Распространенным является представление о
том, что по значению определителя матрицы А можно судить о сте­
пени близости системы уравнений к вырожденной или об обуслов­
ленности системы. Для того чтобы убедиться в ошибочности этого
мнения, умножим каждое из уравнений системы (5.1) на постоян­
ную а "*' О. Ясно, что такое преобразование никак не меняет решение
системы и его чувствительность к малым относительным погрешно­
стям в данных. Однако определитель умножается на число ат
и поэтому с помощью выбора а может быть сделан как угодно боль­
шим или малым. Подчеркнем, что число обусловленности cond(A)
при таком преобразовании системы не меняется в силу свойства 3°.
Замечание 3. Вычисление чисел обусловленности vв(х) =
llA-111 • llbll/llxll и cond(A) = llA-111 • llA 11 непосредственно по ука-
занным формулам предполагает предварительное вычисление обрат­
ной матрицы А- 1 . Вследствие большой трудоемкости этой операции
(как показано в § 5.6, для ее выполнения в общем случае требуется
примерно 2т3 арифметических операций) на практике избегают та­
кого способа вычисления. При этом важно отметить, что в большин­
стве случаев доС1аточно лишь грубой оценки числа обусловленности
с точностью до порядка. С эффективными методами, дающими оцен­
ки величин vь(х) иcond(A), можно познакомиться в (81, 106, 54).
Проверить чувствительность решения системы Ах = Ь к погрешно­
стям можно и экспериментально. Для этого достаточно решить задачу
несколько раз с близкими к Ь правыми частями b(l), Ьщ, "" ь<пJ. Можно
б(х<I))
ожидать, что величина v0= max --(1-1 даст оценку значения vв(х).
1 S/Sn б(Ь )
Во всяком случае она дает оценку снизу, так как v0 :::; Vв(х):::; cond(A).
§ 5.5. Метод Гаусса
Рассмотрим один из самых распространенных методов решения сис­
тем линейных алгебраических уравнений - метод Гаусса 1• Этот метод
(который называют также методо;и последовательного исключения
неизвестных) известен в различных вариантах уже более 2000 лет.
1 Карл Фридрих Гаусс (1777-1855) - не-.~ецкий мате-.~атик и физик, работы которого
оказали большое влияние на дальнейшее развитие высшей алгебры, геометрии, теории
чисел, теории электричества и магнетизма.
145

147. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Во всяком случае, его использовали китайские математики примерно за
250 лет до новой эры.
Вычисления с помощью метода Гаусса состоят из двух основных
этапов, называемых прямым ходом и обратным ходо,w (обратной
подстановкой). Прямой ход метода Гаусса заключается в последова­
тельном исключении неизвестных из системы (5.1) для преобразования
ее к эквивалентной системе с верхней треугольной матрицей. Вычисле­
ния значений неизвестных производят на этапе обратного хода.
1. Схема единственного деления. Рассмотрим сначала простейший
вариант метода Гаусса, называемый схемой единственного деления.
Пр я мой ход состоит из т - 1 шагов исключения.
l - й шаг. Целью этого шага является исключение неизвестного х1 из
уравнении с номерами i = 2, 3, ..., т. Предположим, что коэффициент
а11 *О. Будем называть его главным (или ведущим) элементом 1-го шага.
Найдем величины
(5.29)
называемые множителями 1-го шага. Вычтем последовательно из вто­
рого, третьего, ..., т-го уравнений системы (5.1) первое уравнение,
умноженное соответственно на µ 21 , µ 31 , .•. , µт 1. Это позволит обратить
в нуль коэффициенты при х1 во всех уравнениях, кроме первого. В
результате получим эквивалентную систему
а11Х1 + а12Х2 + а13Х3 + ··· + а1тхт = Ь1 •
(1) (1)
а22 Xz + аzз Хз +
(5.30)
v <1> ь< 1> <. . 2 3 ) Фв которои aij и i 1,1 = , , ... , т вычисляются по ормулам
(1) (1)
a;j =а;гµ;1 а 1j, Ь; =Ь;-µ; 1 Ь 1 • (5.31)
2 - й шаг. Целью этого шага является исключение неизвестного х2
v ( 1) ( 1)
из уравнении с номерами 1 = 3, 4, ..., т Пусть а22 * О, где а22 -
коэффициент, называемый главным (или ведущим) элементом 2-го
шага. Вычислим множители 2-го шага
( 1) ( 1)
µ;2 = а;2 la22 (i = 3, 4, ..., т)
146

148. § 5.5. Метод Гаусса
и вычтем последовательно из третьего, четвертого, "., т-го уравнений
системы (5.30) второе уравнение, умноженное соответственно на
µ 32 , µ 42 , "., µm2 В результате получим систему
а11Х1 + а12Х2 + а13Х3 + ". + almxm = Ь1,
+а0 1х = ь< 1 >2т т 2 •
(2) <2> = ь<2>
а33 Х3 + ··· + а3тХт 3 • (5.32)
Здесь a~j> и ь~2 > (i,j = 3, 4, "., т) вычисляются по формулам
<2> (1) <I> ь~2) = ь~1> - . ь<1>
aij =а;/ - µ;2а2] , , µ,2 2 ·
Аналогично проводятся остальные шаги. Опишем очередной k-й шаг.
k-й шаг. В предположении, что главный (ведущий) элемент k-го
шага ai~- I) отличен от нуля, вычислим множители k-го шага
{k-1) {k-1)
µik=a;k lakk (i=k+,".,т)
и вычтем последовательно из (k + 1)-го, ..., т-го уравнений полученной
на предыдущем шаге системы k-e уравнение, умноженное соответст­
венно на µk + 1, k• µk + 2, k• "., µmk·
Гlосле (т - 1)-ro шага исключения получим систему уравнений
а11Х1+а12Х2+ а13Х3+".+а1тХт = h1,
(2)
а33 Х3 + (5.33)
(т-1) - ь<т-1)
0тт Хт - т '
матрица А (т - 1) которой является верхней треугольной. На этом вычис­
ления прямого хода заканчиваются.
Об ратный ход. Из последнего уравнения системы (5.33) находим
х т. Подставляя найденное значение х т в предпоследнее уравнение,
получаем х т _ 1• Осуществляя обратную подстановку, далее nоследова-
147

149. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
тельно находим хт _ 2,хт _ 3, ... , х1 . Вычисления неизвестных здесь про­
водятся по формулам
- ь<т-)1 (m-1)
хт- т 0тт '
(k-) (k-)
bk -akk+IXk+I
xk = , (k-1)
akk
(5.34)
(k=m-1, ...,).
Труд о ем к о ст ь метод а. Оценим число арифметических опера­
ций, необходимых для реализации схемы единственного деления.
Вычисления -го шага исключения по формулам (5.29), (5.31) тре­
буют выполнения т - 1 деления, (т - )т умножений и (т - l)m
вычитаний, т.е. общее число арифметических операций составляет Q1 =
= 2(т - 1)2 + З(т - ).Аналогично, на 2-м шаге требуется Q2 = 2(т - 2)2 +
+ 3(т - 2) операций, а на k-м шаге - Qk = 2(т - k)2 + 3(т - k) операций.
Подсчитаем теперь приближенно общее число Q арифметических
операций прямого хода, считая размерность системы т достаточно
большой:
m-1 m-1 m-1 m-1 m-1
Q= L Qk=2 L (m-k)2 +3 L (m-k)=2 L k2 +3 L k=
k= k=I k=I ~=! k=I
_ 2(т - 1)т(2т - 1) З(т - 1)т 2 3
- б + 2 ~зт.
Как нетрудно видеть, для реализации обратного хода по формулам
(5.34) нужно всего т2 операций, что при больших т пренебрежимо
мало по сравнению с числом операции прямого хода.
Таким образом, для реализации метода Гаусса требуется примерно
(2/3)т3 арифметических операций, причем подавляющее число этих
действий совершается на этапе прямого хода.
Пример 5.7. Методом Гаусса решим систему
Прямой ход.
Ох 1 + бх2 + 2х3 = 25,
5х 1 + х2 - 2х3 + 4х4 = 14,
3х 1 + 5х2 + х3 - х4 = 10,
6х2 - 2х3 + 2х4 = 8.
(5.35)
1-й шаг. Вычислим множители µ 21 = а21 /а 11 = 5/10 = 0.5, µ 31
=а31 /а11 = 3/10 =0.3, µ 41 = а41 /а 11 = 0/10 =О. Вычитая из второго,
148

150. § 5.5. Метод Гаусса
третьего и четвертого уравнений системы (5.35) первое уравнение,
умноженное на µ21' µ 31 и µ41 соответственно получаем:
!Ох 1 + 6х2 + 2х3 = 25,
2х2 - 3х3 + 4х4 = 1.5,
3.2х2 + О.4х3 - х4 = 2.5,
6х2 - 2х3 + 2х4 = 8.
(5.36)
2 () (1) 3-й шаг. Вычислим множители µ32 = а32 /а22 = .2/(-2) = -1.6,
µ 42 = 6/(-2) = -3. Вычитая из третьего и четвертоm уравнений системы
(5.36) второе уравнение, умноженное на µ 32 и µ 42 соответственно, при­
ходим к системе
25,
- 2х2 - 3х3 + 4х4 = 1.5,
- 4.4х3 + 5.4х4 = 4.9,
(5.37)
- l lx3 + 14х4 = 12.5.
3- й шаг. Вычисляя множитель µ43 = (-11)/(--4.4) = 2.5 и вычитая из
четвертоm уравнения системы (5.37) третье уравнение, умноженное на
µ43, приводим систему к треуmльному виду:
= 25,
- 2х2 - 3х3 + 4х4 = 1.5,
- 4.4х3 + 5.4х4 = 4.9,
(5.38)
О.5Х4 = 0.25.
Обратный ход. Из последнего уравнения системы находим
х4 ~ 0.5. Подставляя значение х4 в третье уравнение, находим х3 =
= (4.9 - 5.4х4)/(--4.4) = -0.5. Продолжая далее обратную подстановку,
получаем х2 = (1.5 + 3х3 - 4х4)/(-2) = 1, х 1 = (25 - 6х2 - 2х3)/10 = 2.
Итак, х 1 =2, х2 = 1, х3 =-0.5, х4 = 0.5.
Результаты вычислений приведены в табл. 5.2. А
Необходимость выбора главных элементов. Заметим, что
вычисление множителей, а также обратная подстановка предполагают
(k - 1)
деление на главные элементы akk Поэтому если один из главных
149

151. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Таблица 5.2
Наименование а,1 а,2 а,3 а,4 ь, µ,1' х1
Исходная система 10 6 2 о 25 -
5 1 -2 4 14 -
3 5 1 -1 10 -
о 6 -2 2 8 -
1-й шаг прямого хода 10 6 2 о 25 -
о -2 -3 4 1.5 0.5
о 3.2 0.4 -1 2.5 0.3
о 6 -2 2 8 о
Z-й шаг прямого хода 10 6 2 о 25 -
о -2 -3 4 1.5 -
о о -4.4 5.4 4.9 -1.6
о о -11 14 7.5 -3
3-й шаr прямого хода 10 6 2 u 25 2
и обратный ход о -2 -3 4 1.5 1
о о -4.4 5.4 4.9 -0.5
о о о 0.5 0.25 0.5
элементов оказывается равным нулю, то схема единственного деления
не может быть реализована. Здравый смысл подсказывает, что и в
ситуации, когда все главные элементы отличны от нуля, но среди них
есть близкие к нулю, возможен неконтролируемый рост погрешности.
Пр им ер 5.8. Используя метод Гаусса, решим систему уравнений
2х 1 - 9х2 + 5х3 = -4,
1.2х 1 - 5.3999х2 + 6х3 = 0.6001, (5.39)
Х1 - Х2 - 7.5х3 = -8.5
на 6-разрядном десятичном компьютере.
Прямой ход.
1-й шаг. Вычисляем множители µ21 = 0.6 и µ31 = O.S и преобразуем
систему к виду
2х 1 - 9х2 + 5х3 = -4,
О.0001х2 + 3х3 = 3.0001,
3.5х2 - 10х3 = -6.5.
Все вычисления на этом шаге выполняются без округлений.
(5.40)
2-й шаг. После вычисления множителя µ32 = 3.5/0.0001 = 35 ООО
последнее уравнение системы должно быть преобразовано к виду
150

152. § 5.5. Метод Гаусса
а~;>хз = ь~2 >. где а~;) = -10- 3· µ 32 = -105 010, Ь~2 ) =-6.5 - 3.0001· µ 32 =
= -105 010. Однако на используемом компьютере будет получено
уравнение
-105 010х3 = -!05 011. (5.41)
Действительно, коэффициент а~;> определяется точно, так как при его
вычислении не возникает чисел, мантиссы которых имеют более шести
разрядов. В то же время при вычислении b~2 J умножение коэффициента
3.0001 на µ32 дает 7-разрядное число !05 003.5, после округления кото-
рого до шести разрядов получится 105 004. Вычисление Ь~2 ) завер­
шается выполнением операции вычитания: Ь~2 ) ,., -6.5 - 105 004 =
= -105 О 10.5. После округления последнего числа до шести разрядов
мантиссы приходим к уравнению (5.41).
Обратный ход. Из уравнения (5.41) находим х3 ,., 1.00001. Срав­
нение с истинным значением х3 = 1 показывает, что эта величина полу­
чена с очень высокой для используемого компьютера точностью.
Дальнейшие вычисления дают
х2 = (3.0001 - 3х3)/О.ООО = (3.0001 - 3.00003)/0.0001 = 0.7;
х1 = (--4 + 9х2 - 5х3)/2 = (--4 + 6.3 - 5.00005)/2 = -1.350025.
После округления. имеем х 1 = -1.35003.
Как нетрудно видеть, найденные значения неизвестных имеют мало
общего с истинными значениями решения х 1 = О, х2 = 1, х3 = 1.
В чем же причина появления такой значительной погрешности?
Говорить о накоплении ошибок округления не приходится, так как
всего было выполнено 28 арифметических операций и лишь в четырех
случаях потребовалось округление. Предположение о плохой обуслов­
ленности системы не подтверждается; вычисление cond =(А) дает зна-
чение, равное примерно 100.
В действительности причина состоит в использовании на 2-м шаге
малого ведущего элемента ai;> =О.ООО. Следствием этого стало появле­
ние большого множителя µ 32 и существенное возрастание коэффициен­
тов в последнем уравнении системы. •
Таким образом, изложенный выше вариант метода Гаусса (схема
единственного деления) оказался некорректным и, следовательно, непри­
годным для вычислений на компьютере. Этот метод может привести
151

153. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
к делению на нуль (если ai~-1) = О при некотором k), и вычисления по
нему могут оказаться неустойчивыми.
2. Метод Гаусса с выбором главного элемента по столбцу (схема
частичного выбора).
Оп и с ан и е метод а. На k-м шаге прямого хода коэффициенты урав­
нений системы с номерами l = k + 1, .", т преобразуются по формулам
(k) <k-1) (k-1) ь<kJ_ь<*-'> ь<*-'> . k 1 <542>0u =аи -µ;kakj • ; - ; -µik k • 1 = + , "., т. ·
Интуитивно ясно, что во избежание сильного роста коэффициентов
системы и связанных с этим погрешностей нельзя допускать появления
больших множителей µik·
В методе Гаусса с выбором главного элемента 1 по столбцу гаранти­
руется, что /µikl ~ 1 для всех k = 1, 2, "., т - 1 и z= k + 1, "., т. Отли­
чие этого варианта метода Гаусса от схемы единственного деления
заключается в том, что на k-м шаге исключения в качестве главного
(k- 1)
элемента выбирают максимальный по модулю коэффициент а; k при
k
неизвестной xk в уравнениях с номерами i = k, k + l, "., т. Затем соот­
ветствующее выбранному коэффициенту уравнение с номером ik
меняют местами с k-м уравнением системы для того, чтобы главный
(k- l)
элемент занял место коэффициента akk .
После этой перестановки исключение неизвестного xk производят,
как в схеме единственного деления.
Пример 5.9. Решим систему уравнений (5.39) методом Гаусса с
выбором главного элемента по столбцу на 6-разрядном десятичном
компьютере.
Прямой ход.
1- й шаг. Максимальный в первом столбце элемент матрицы нахо­
дится в первой строке, поэтому перестановка уравнений не нужна.
Здесь 1-й шаг проводится точно так же, как и в примере 5.8.
2-й шаг. Среди элементов а~~) = 0.0001 и а~~) = 3.5 матрицы сис­
темы (5.40) максимальный по модулю принадлежит третьему уравне­
нию. Меняя местами второе и третье уравнения, получаем систему
152
2х 1 - 9х2 + 5х3 = -4,
3.5х2 - 10х3 = -6.5,
О.0001х2 + Зх3 = 3.0001.
1 Выбор главного элемента иногда называют пивотированием.

154. § 5.5. Метод Гаусса
После вычисления µ 32 = 0.0001/3.5 "'2.85714 • 10-5 последнее урав­
нение системы преобразуется к виду 3.00029х3 = 3.00029.
Обратный ход. Из последнего уравнения находим х3 = 1. Далее,
имеем х2 =(-б.5 + 1Ох3)/3.5 = 1, х1 = (--4 + 9х2 - 5х3)/2 = (--4 + 9 - 5)/2 = О.
В данном случае ответ получился точным. •
Заметим, что дополнительная работа по выбору главных элементов
в схеме частичного выбора требует порядка т2 действий, что практиче­
ски не влияет на общую трудоемкость метода.
Вычислительная устойчивость схемы частичного
в ы бор а. Детальное исследование метода Гаусса показывает, что дейст­
вительной причиной неустойчивости схемы единственного деления явля­
ется возможность неограниченного роста элементов промежуточных мат­
риц А (1 >, А <2>, "., А (т -- 1>в процессе прямого хода. Так как на k-м шаге
схемы частичного выбора 1µ ik 1~ 1, то для вычисленных по формулам
(5.42) элементов а~:) справедлива оценка la~1k)j ~ la~:- 1 >1 + la~~- 1 >1.
Следовательно, максимальное по модулю значение элементов матрицы
возрастает на одном шаге не более чем в 2 раза и в самом неблагоприятном
случае т - 1 шаг прямого хода даст коэффицие11т роста <р(т) = 2т - 1•
Гарантия ограниченности роста элементов матрицы делает схему
частичного выбора вычислительно устойчивой. Более того, для нее ока­
зывается справедливой следующая оценка погрешности:
(5.43)
Здесь х* вычисленное на компьютере решение системы; о(х*)
= //x-x*ll 21llx//2 - его относительная погрешность; condE(A)
= llAllEllA-111E - число обусловленности матрицы А; &м - машинное
эпсилон; наконец, /(т) = С(т) <p(m), где С(т) - некоторая медленно
растущая функция, зависящая от порядка т системы (типа степенной
функции с небольшим показателем).
Наличие в оценке (5.43) множителя <р(т) = 2т - 1 указывает на то,
что при большом т схема частичного выбора может оказаться плохо
обусловленной и возможна существенная потеря точности. Однако
практика матричных вычислений показывает, что существенный рост
элементов матрицы происходит крайне редко. В подавляющем боль­
шинстве случаев действительное значение коэффициента роста не пре­
вышает 8-1 О. Если система хорошо обусловлена, то погрешность
вычисленного решения оказывается, как правило, малой.
Иногда для проверки качества приближенного решения х* вычис­
ляют невязку r = Ь -Ах* и о степени близости приближенного решения
153

155. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
к точному пытаются судить по тому, насколько мала невязка. Этот
метод ненадежен по отношению к схеме частичного выбора, так как
известно, что она гарантированно дает малые невязки. Более точно это
утверждение можно сформулировать так: справедлива оценка
(5.44)
где f(m) то же, что и в оценке (5.43). Заметим, что в неравенство (5.44)
не входит число обусловленности.
3. Метод Гаусса с выбором главного элемента по всей матрице
(схема полного выбора). В этой схеме допускается нарушение естест­
венного порядка исключения неизвестных.
На 1-м шаге метода среди элементов aij определяют максимальный
по модулю элемент а; 1· . Первое уравнение системы и уравнение с
1 1
номером i 1 меняют местами. Далее стандартным образом производят
исключение неизвестного xj 1 из всех уравнений, кроме первого.
(k- 1)
На k-м шаге метода среди коэффициентов a;j при неизвестных
в уравнениях системы с номерами i = k, ..., т выбирают максимальный
(k-1)
по модулю коэффициент а; 1· . Затем k-e уравнение и уравнение,
k k
содержащее найденный коэффициент, меняют местами и исключают
неизвестное xjk из уравнений с номерами i = k + 1, ..., т.
На этапе обратного хода неизвестные вычисляют в следующем
порядке: xjm, xjm- I, "., xj1.
Пример 5.10. Решим систему (5.39), использовав схему полного
выбора на 6-разрядном десятичном компьютере.
Прямой ход.
1- й шаг. Максимальный по модулю элемент а 12 =-9 содержится в
первом уравнении, поэтому перестановка уравнений не нужна. Исклю­
чаем неизвестное х2 из второго и третьего уравнений, используя мно-
жители µ 21 = -5.3999/(-9)::::: 0.599989 и µ 31 = -1/(-9)::::: 0.111111. В
результате получаем систему
2х 1 - 9х2 + 5х3 = -4,
О.000022х 1 + 3.00006х3 = 3.00006,
О.777778х 1 - 8.05556х3 = -8.05556.
154

156. § 5.5. Метод Гаусса
2- й шаг. Среди коэффициентов при неизвестных во втором и тре­
тьем уравнениях максимальным по модулю является коэффициент а~~> =
= - 8.05556. Переставляя местами второе и третье уравнения и исключая
неизвестное х3 (соответствующий множитель µ32 = 3.00006/(-8.05556) "'
"' -0.372421 ), приходим к системе
2х 1 - 9х2 + 5х3 = -4,
О.777778х 1 - 8.05556х3 = -8.05556,
О.289683х 1 = 2.89240. 10-7 .
Обратный ход. Из последнего уравнения находим х1
= 2.89240 · 10-7/0.289683 "'9.98470 · 10-7. Далее, имеем х3 = (-8.05556 -
- О.777778х 1 )/(-8.05556)"' 1.00000, х2 = (-4 - 2х 1 - 5х3)/(-9)"' 1.00000.
Округляя найденные значения до пяти цифр после десятичной
точки, получим ответ: х1= 0.00000, х2 = 1.00000, х3 = l .00000. Заметим,
что в данном случае получено решение, совпадающее с точным. .&
Схема полного выбора по сравнению со схемой частичного выбора
дает существенное замедление роста элементов матрицы. Доказано, что
для нее коэффициент роста <p(m), входящий в оценку (5.43), не превы­
шает значения т112 (21.3112.4113 ". mI/(m-1))112 ~ l.8ml12m025lnm (что
значительно меньше соответствующего значения <р(т) = 2т - 1 для
схемы частичного выбора). Более того, длительное время существовала
гипотеза Уилкинсона, согласно которой для схемы полного выбора
<р(т) ~ т. Только в 1991 г. была найдена1 матрица 13-го порядка, для кото­
рой <р(JЗ) = 13.025 > 13. Таким образом, для хорошо обусловленных систем
этот вариант метода Гаусса является хорошо обусловленным.
Однако гарантия хорошей обусловленности достигается здесь ценой
значительных затрат на выбор главных элементов. Для этого дополни­
тельно к (2/3)т3 арифметическим действиям требуется произвести при­
мерно т3/3 операций сравнения, что может ощутимо замедлить про­
цесс решения задачи на компьютере2 . Поэтому в большинстве случаев
на практике предпочтение отдается все же схеме частичного выбора.
Как уже отмечено выше, ситуации, когда при использ.>вании этого
варианта метода Гаусса происходит существенный рост элементов,
1 N. Gould. Оп growth in Gaussian elimination with complete pivoting // SIAM J. Matrix
Anal. Арр. 1991. Vol. 12 (2). Р.354-361.
2 Заметим, что на современных высокопроизводительных компьютерах операции
с плавающей точкой выполняются почти так же быстро, как и операции сравнения.
155

157. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
встречаются чрезвычайно редко. Более того, эти ситуации могут быть
легко выявлены с помощью заложенных в современных программах
эффективных методов слежения за ростом элементов матриц.
4. Случаи, когда выбор главных элементов не нужен. Известно
что, для некоторых классов матриц при использовании схемы единст­
венного деления главные элементы гарантированно располагаются на
главной диагонали и потому применять частичный выбор нет необхо­
димости. Так, например, обстоит дело для систем с симметричными
положительно определенными матрицами, а также с матрицами, обла­
дающими свойством строчного диагонального преобладания:
т
L /aij/ </а;;/, i = 1, 2, ..., т.
j= 1
j"'i
(5.45)
Матрицы, удовлетворяющие условию (5.45), таковы, что в каждой
из строк модуль элемента а", расположенного на главной диагонали,
больше суммы модул~й всех остал.J>ных элементов строки.
5. Масштабирование. Перед началом решения целесообразно мас­
штабировать систему так, чтобы ее коэффициенты были величинами
порядка единицы.
Сушест11уют два естественных способа масштабирования' системы
Ах = Ь. Первый заключается в умножении каждого из уравнений на
некоторый масштабирующий множитель µ1 • Второй состоит в умноже-
нии на масштабирующий множитель а.1 каждого }-го столбца матрицы,
-1
что соответствует замене переменных xj = a.j xj (фактически - это
замена единиц измерения). В реальных ситуациях чаще всего масшта­
бирование может быть выполнено без существенных трудностей.
Однако подчеркнем, что в общем случае удовлетворительного способа
масштабирования пока не найдено.
На практике масштабирование обычно производят с помощью деле­
ния каждого уравнения на его наибольший по модулю коэффициент
либо на евклидову норму соответствующей строки матрицы А. Это
вполне удовлетворительный способ для большинства реально встре­
чающихся задач.
1 Иногда эту операцию называют уравновешиванием.
156

158. § 5.6. Метод Гаусса и решение систем уравнений, обращение матриц
§ 5.6. Метод Гаусса и реwение систем уравнений
с несколькими правыми частями, обращение матриц,
вычисление определителей
Рассмотрим применение метода Гаусса к решению следующих задач
линейной алгебры:
1) вычисление решений системы уравнений с несколькими пра-
выми частями;
2) вычисление обратной матрицы;
3) вычисление определителя.
1. Вычисление решений системы уравнений с несколькими
правым частями. Довольно часто на практике встречается ситуация,
когда нужно решить несколько систем уравнений
Ах= d(l)' Ах= d(2)' ... , Ах= d(p) (5.46)
с одной матрицей А и различными правыми частями d(I)' d(Z)• ..., d(p)·
Конечно, применив метод Гаусса к каждой из систем (5.46) незави­
симо от других, можно найти соответствующие решениях0 ),х(Z)• ...,х(р)•
затратив примерно (2/З)рт 3 арифметических операций. Однако при
одновременном решении систем (5.46) число операций можно сущест­
венно сократить. Как было отмечено в § 5.5, основные вычислитель­
ные затраты в методе Гаусса связаны с преобразованием матрицы
к треугольному виду. Преобразование же правой части производится
параллельно и требует примерно т2 арифметических операций. Если
параллельно с приведением матрицы А к треугольному виду преобра­
зовать по однотипным формулам все р правых частей, то на прямой
ход метода будет затрачено только примерно (2/З)т 3 + рт 2 операций.
С учетом обратного хода общие вычислительные затраты составят
примерно (2/З)т3 + 2рт2 арифметических операций.
Преобразование правых частей не обязательно производить парал­
лельно. Каждую из правых частей d(I)• d(Z)• ..., d(p) можно обработать
последовательно, если после приведения матрицы А к треугольному виду
А (т - 1) сохранить в памяти компьютера множители µ11 и матрицу А <т - 1>.
2. Вычисление обратной матрицы. Прежде чем переходить к
изложению метода вычисления обратной матрицы А-1 для квадратной
невырожденной матрицы А, отметим, что в действительности про­
блема вычисления обратной матрицы возникает не так часто, как это
можно предполагать.
К сожалению, нередко обращение матрицы А производится с единст­
венной целью вычислить по известному вектору Ь вектор х видах= л- 1 ь.
Умножение матрицы А- 1 на вектор требует примерно 2т 2 арифметиче­
ских операций. Однако вычисление А-1 обходится (как будет показано
157

159. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
ниже) примерно в 2т3 операций. Это означает, что на вычисление
решения системы Ах = Ь по формуле х = А-1 ь будет затрачено при­
мерно 2т3 операций. В данном случае х можно найти в 3 раза быстрее
методом Гаусса и вычисление А-1 не нужно. Более того, можно ожи­
дать, что вычисленное методом Гаусса решение окажется точнее, так
как потребуется выполнение меньшего числа операций.
Может показаться особенно выгодным предварительное вычисле­
ние матрицы А-1 , если далее потребуется найти большое число векто­
ров по формулам
x(I) =A-1d11 ), хщ =A-1d<2>, .. " х(р) =A-1d(p)" (5.47)
Однако суммарные затраты при таком подходе составят примерно
2т3 + 2рт2 операций, в то время как при одновременном решении мето­
дом Гаусса эквивалентных систем (5.46) получаем значения x(l)• х(2), ".
"" х(р) примерно за (2/3) т3 + 2рт2 операций. Следовательно, и в этом
случае вычисление л-1 нецелесообразно.
Иногда в пользу необходимости вычисления л- 1 приводится сле­
дующий довод. Если известно, что в течение длительного времени
потребуется неоднократно решать системы уравнений вида (5.46) с
фиксированной матрицей А и различными правыми частями d(k)• то
имеет СМЫСЛ предварительно вычислить л-1 . Записав л-1 в память
компьютера можно затем по мере необходимости быстро вычислить
x(k) по формуле хщ = A-1d(k). Однако использование LU-разложения
матрицы А (см. § 5.7) позволяет вычислять x(k) столь же быстро, а
предварительная работа на этапе разложения дает трехкратную эконо­
мию. Таким образом, и этот довод в пользу необходимости вычисле­
ния обратной матрицы неубедителен.
Довольно часто при решении различных задач средствами линейной
алгебры возникают выражения типа
v = в-1cл-1 wv-1 w. (5.48)
Если у исследователя нет достаточного опыта решения задач линейной
алгебры на компьютере, то он может принять решение о необходимо­
сти вычислять матрицы в-1,л-1, D- 1, чтобы действовать далее по фор­
муле (5.48). Однако и в этом случае, можно поступить иначе и найти v
с меньшими затратами. Решив систему Dx = w, найдем х = D-1w. Затем
вычислим у= Wx и, решив систему Az =у, найдем z = л- 1у. Наконец,
вычислим и= Cz и, решив систему Bv =и, найдем v = в- 1 и.
Сказанное выше вовсе не означает, что нет ситуаций, когда вычис­
ление матрицы л-1 необходимо и оправдано. В ряде технических при­
ложений и статистических задач непосредственный интерес представ­
ляет анализ свойств именно обратной матрицы. Тем не менее, как мы
158

160. § 5.6. Метод Гаусса и решение систем уравнений, обращение матриц
видим, в матричных вычислениях можно и следует обходиться без
вычисления обратных матриц. Авторы настоятельно рекомендуют не
вычислять обратные матрицы, если только в дальнейшем не предпола­
гается анализ элементов этих матриц.
Покажем, как вычисление обратной матрицы можно свести к рас­
смотренной выше задаче решения системы уравнений с несколькими
правыми частями. Обозначим матрицу А- 1 через V, ее столбцы - через
v 1, v2, "" vm и столбцы единичной матрицы Е - через е1 , е2, "" ет.
Согласно определению обратной матрицы верно равенство AV = Е,
эквивалентное совокупности равенств
Av1= е1 , Av2 = е2, "" Avm = ет. (5.49)
Таким образом, столбцы матрицы V = А- 1 (а следовательно, и саму
матрицу), можно найти, решив т систем уравнений с общей матрицей
А. Согласно изложенному выше, для этого потребовалось бы при­
мерно (8/З)т3 арифметических операций, однако учет специального
вида правых частей системы (5.49) позволяет вычислять матрицу А-1
примерно за 2т3 операций.
3. Вычисление определителя. Воспользуемся алгоритмом метода
Гаусса с выбором главного элемента по столбцу и заметим, что иско­
мый определитель и определитель полученной треугольной матрицы
А(т - I) связаны равенством
detA = (-1 )5 det А(т - 1),
где s - число потребовавшихся перестановок строк. Остается восполь­
зоваться формулой (5.17), и тогда получим
_ , (О) (1) (m-1)
detA - (-1) а 11 а22 ". атт , (5.50)
где а~> = а11 • Отметим, что вычисление по формуле (5.50) требует осо­
бой аккуратности, в особенности если число т велико. Как мы убеди­
лись в примере 3.29, при вычислении произведений следует специаль­
ным образом упорядочивать сомножители. Неудачный порядок их
расположения может привести к получению результата, равного ±оо, или
к существенной потере точности.
Этого можно избежать, если для вычисления det А воспользоваться
формулой
Однако следует иметь в виду, что ее использование может привести к
некоторой потере точности.
159

161. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
3 а меч ан и е. Действительная необходимость в вычислении
определителей возникает довольно редко Во всяком случае осtю­
ванные на их использовании алгоритмы оказываются весьма неэф­
фективными (как в примере 3.34, где обсуждалось правило Кра­
мера), и поэтому вычисление определителей давно уже не является
элементом современных алгоритмов линейной алгебры. Кроме
того, из результатов в § 5.4 следует, что использование величины
detA для определения степени близости системы уравнений к
вырожденной дает весьма ненадежный и сомнительный критерий.
Пр им ер 5.11. Использовав метод Гаусса с выбором главного эле­
мента по столбцу, вычислим определитель матрицы
r
2 -9 51А= 1.2 -5.3999 6
1 -) -7.5
на 6-разрядном десятичном компьютере.
Повторив преобразования из примера 5.9, получим матрицу
r
2 -9 5 1А(2> = О 3.5 -10 ·
о о 3.00029
Так как была сделана одна перестановка строк, то формула (5.50) дает
det(A) "" (-1) • 2 · 3.5 · 3.00029 "" -21.0020. _.
Можно с достаточной степенью уверенности предположить, что во
многих технических науках, где традиционно используются определи­
тели, в ближайшее время неизбежен переход к использованию других,
более содержательных характеристик линейных моделей. Такими есте­
ственными характеристиками могут служить, например, собственные
числа и собственные векторы матриц (см. гл. 8).
§ 5.7. Метод Гаусса и разложение матрицы
на множители. LU.разложение
Вернемся еще раз к методу Гаусса, чтобы рассмотреть его с более
обших позиций. Излагаемый ниже подход оказался чрезвычайно плодо­
творным и привел не только к более глубокому пониманию метода, но и
позволил со1дать высокоэффективные машинные алгоритмы его реализа­
ции, а также рассмотреть другие точные методы с единой точки зрения.
160

162. § 5.7. Метод Гаусса и разложение матрицы на множители. Ш-разложение
Рассмотрим сначала простейший вариант метода Гаусса для реше­
ния системы линейных алгебраических уравнений
Ах=Ь. (5.51)
1. Схема единственного деления и LU-раЗJiожение. При выполне­
нии вычислений 1-го шага исключения по схеме единственного деле­
ния система уравнений приводится к виду
А (l)x = b(I), (5.52)
где
0 11 0 12 °13 ··· 0 1т Ь1
о
( 1) ( 1) ( 1) b(l)
0 22 °23 02т 2
A(I)=
о
( 1) ( 1) ( 1)
'
ьо>= b(I)
'О32 О33 03т 3
( 1) ( 1) ( 1)
О От2 От3 · · · Отт
b(I)
т
а ~оэффициенты 0< 1> b(I) (" · 2 3 ) ф" ,1 , , 1,1 = , , ..., т вычисляются по ормулам
(5.29), (5.31).
Введем матрицу
о о ... о
-µ21 1 о ... о
М1 = -µ31 О 1 ... О
-µml О О ... l
Как нетрудно проверить, справедливы равенства
A(I) = М 1 А, b(l) = М1Ь,
т.е. преобразование системы (5.51) к виду (5.52) эквивалентно умноже­
нию левой и правой частей системы на матрицу М1 .
Аналогично можно показать, что вычисления 2-го шага исключения
приводят систему (5.52) к виду
А(2 >х = Ь(2),
где
161

163. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
0 11 0 12 0 1з ... о1,,.
о о ... о
Ь1
о
( 1) ( 1) (1)
о о ... о
b(I)
022 °23 ··· о2,,. 2
А(2)=
о о
(2) (2)
'
М2= о -µ32 1 ... о
'
ь<2> = ь<2>
033 О3,,, 3
............. . . . . ... . ... ....
(2) (2) о -µ,,,2 о ... 1 ь<2>о о о,,. 3 ... о,,.,,. т
После (т - 1)-го шага, завершающего прямой ход, система оказыва­
ется приведенной к виду
А<т- l>х = ь<m-1) (5.53)
с верхней треугольной матрицей А <т - 1). Здесь
л<m-1) =М,,,_1А"'-2, ь<т-1) =М,,,_1ь<т-2>,
где
0 11 0 12 0 13 ... 0 1т
о о1 о о
о
( 1) ( 1) ( 1)
0 22 °23 02т о 1 о о о
(2) (2)л<m-1)=
о о О33 ••. о3,,.
.М,,,_1= ................... '
о о
(m-1)
О ... о,,.,,.
Ь1
b~I)
ь<т-1)= ь<2)
3
ь<т- 1)
т
о о о о
О О О ... -µт,т-1 l
Заметим, что матрица А(т - I) получена из матрицы А последова­
тельным умножением на М1, М2, ..., М,,, _ 1:
А(т-I>=М,,,_ 1 ... М2М1 А. (5.54)
Аналогично,
ь<т-1) = М,,,_ 1 ." М2 М1 Ь. (5.55)
Из равенства (5.54) вытекает следующее представление:
_ -1 -1 -1 (m-l)
А-М1 М2 ... М,,,_ 1А . (5.56)
162

164. § 5.7. Метод Гаусса и разложение матрицы на множители. Ш-разложение
Как легко проверить,
о о о
µ21 1 о о
-1
М1 = µ31 О 1 ". О ,
µml О О ." 1
1 о о
о 1 о
о о о
м-1_
2 -
1 о о о
о о о
о µ32 о
............
О µm2 О ." 1
о о
о о
о
О О О ". µm, т - 1 1
' ...,
-1
Для этого достаточно перемножить матрицы Mk и Mk (k = 1, ."
.. " т - 1), в результате чего получится единичная матрица.
Введем обозначения и= А (т - 1>, L = M1-I M2-I ". м,;;-~ 1. Вычисляя
матрицу L, убеждаемся в том, что она имеет следующий вид:
о о о
µ21 о о
L= µ31 µ32 о (5.57)
...............
µml µm2 µmЗ ". 1
Тогда равенство (5.56) в новых обозначениях примет вид
А = LU. (5.58)
Это и есть 1 LИ-разложение матрицы А - представление матрицы
А в виде произведения нижней треугольной матрицы L и верхней тре­
угольной матрицы U.
Таким образом, прямой ход метода Гаусса без перестановок можно
рассматривать как процесс вычисления LИ-разложения матрицы сис­
темы, на k-м шаге которого определяются элементы k-го столбца мат­
рицы L и k-й строки матрицы U.
Возможность LИ-разложения обосновывается следующей теоремой.
1 Обозначения треугольных матриц буквами L и U вызваны тем, что эти буквы явля­
ются начальными в английских словах lower - «нижний» и upper - «верхний».
163

165. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Теорем а 5.3. Если все главные миноры матрицы А отличны от
нуля, то существуют единственные ни:жняя треугольная матрица L
вида (5.57) и верхняя треугольная матрица U такие, что А = LU. •
Структура матриц L и U позволяет организовывать компактное раз­
мещение элементов этих матриц в памяти компьютера по мере их
вычисления. На k-м шаге исключения в области памяти, где первона­
чально располагалась матрица А, размещается матрица
al,k+ 1
( 1)
a2,k+ 1
(k-1) (k-1)
akk ak,k+ 1
(k)
µk+l,k ak+l,k+I
(k)
am,k+
(k- 1)
akm
(k)
ak+ 1,m
При этом вся необходимая для дальнейших вычислений информация
сохраняется.
Пр им ер 5.12. Проиллюстрируем LU-разложение на примере реше­
ния системы (5.35). На основании данных табл. 5.2 можно записать
L = r~.5 ~0.3 -1.6
о -3
о
о
1
2.5
01 [ 10 6 2 о 1О U= О -2 -3 4
о ' о о -4.4 5.4 .
1 о о о 0.5
Следовательно, LU-разложение матрицы системы имеет вид
[~о 6 -~ ~1=[~.5 о ~ ~1·[~0-~ _: ~ 1·.
3 5 -1 0.3 -1.6 1 о о о -4.4 5.4
о 6 -2 .2 о -3 2.5 1 о о о 0.5
2. Использование LU-разложения. В современных программах,
реализующих метод Гаусса на компьютере, вычисления разбивают на
два основных этапа. Первый этап - это вычисление LU-разложения
матрицы системы. Второй этап - обработка правых частей и вычисле­
ние решения.
164

166. § 5.7. Метод Гаусса и разложение матрицы на множители. Ш-разложение
Смысл выделения первого этапа состоит в том, что он может быть
выполнен независимо, для его проведения не нужна информация о пра­
вой части системы. Это как бы этап предварительной подготовки к
быстрому вычислению решения. Именно для получения LU-разложе­
ния производится основная масса вычислений (примерно (2/3)m3 ариф­
метических операций).
На втором этапе выполняют следующие действия:
1°. Преобразуют правую часть Ь по формулам прямого хода; необхо­
димые для вычисления коэффициенты µ ,1 берут из матрицы L. В резуль-
тате получают вектор ь<т - 1>, связанный с вектором Ь формулой (5.55).
2°. С помощью обратной подстановки решают систему Ux = ь<т - 1>.
Для непосредственного вычисления решения х на втором этапе тре­
буется примерно 2m2 арифметических операций.
В случае, если необходимо решить р систем уравнений (5.46) с фик­
сированной матрицей А и различными правыми частями d(I)' d(2), ..., d(p)'
первый этап проводят лишь один раз. Затем последовательно р раз про­
водят вычисления второго этапа для получения решенийх( 1 )'х(2)' ...,х(р)·
Для этого, как и в§ 5.6, требуется примерно (2/3)m2 + 2рт2 арифмети­
ческих операций.
Пр им ер S.13. Решим систему
10х 1 + 6х2 + 2х3 = 8,
5х 1 + х2 - 2х3 + 4х4 = 7,
3х 1 + 5х2 + х3 - х4 = 2,
6х2 - 2х3 + 2х4 = 2.
Воспользуемся LИ-разложением матрицы системы, указанным в
примере 5.12. Сначала преобразуем вектор правой части Ь = (8, 7, 2, 2)т
по формулам прямого хода.
1-й шаг. Ь~1 ) =Ь2 -µ 21 Ь1 =7-0.5·8=3, Ь~1 ) =b3 -µ 3ib1 =2-
- 0.3 · 8 = -0.4, Ь~1 > = Ь4 - µ 41 Ь1 =2- О· 8 = 2. После 1-го шага получим
ь< 1 > = (8, 3, -0.4, 2)т.
2-й шаг. ь~2 >=ь~1 >-µ32Ь~1 > = -0.4 - (-1.6)·3 = 4.4, Ь~2 >=ь~1 > -
- µ42Ь~1 > = 2 - (-3) · 3 = 11. После 2-го шага найдем ь<2> = (8, 3, 4.4, 11)7:
165

167. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
3 -й шаг. Ь~3 ) =ь~2> - µ43Ь~2) = 11 - 2.5. 4.4 =о. в результате прямого
хода получен вектор Ь(З) = (8, 3, 4.4, О)Т и система приведена к виду
10х 1 + 6х2 + 2х3 = 8,
- 2х2 - 3х3 + 4х4 = 3,
- 4.4х3 + 5.4х4 = 4.4,
О.5Х4 =о.
Обратный ход дает значения неизвестных х4 =О, х3 =-1, х2 =О, х1 = 1. •
3. Метод Гаусса с выбором главного элемента и разложение мат­
рицы на множители. В отличие от схемы единственного деления
схема частичного выбора предполагает на k-м шаге прямого хода пере­
становку уравнений системы с номерами ik и k (при выборе в качестве
(k- 1)
главного элемента k-го шага элемента а, k ). Это преобразование
k
эквивалентно умножению системы на матрицу Pk, которая получается
из единичной матрицы перестановкой ik-й и k-й строк (см. пример
5.14). Исключение неизвестного на k-м шаге по-прежнему эквива­
лентно умножению системы на матрицу Mk.
Таким образом, после 1-го шага система Ах = Ь преобразуется к
виду A(l>x = ьо>, где А< 1 > =М1Р1А, ь< 1 > =М1Р1Ь. После 2-го шага сис-
тема преобразуется к виду А<2>х = Ь(2), где А<2> = М2Р2АО>, ь<2> =
=M2P2b<I>.
После завершающего (т - 1)-го шага прямого хода система оказывается
приведенной к виду А<т - 1 >х = ь<т - 1>, где А<т - 1>= Мт _ 1 Рт_ 1 А<т - 2>,
ь<т-1) = Мт- iPт- 1ь<т-2)_
Как нетрудно видеть,
А<т-1)=Мт-1Рт-1 ... М2Р2М1Р1А, (5.59)
(5.60)
Равенство (5.59) равносильно следующему разложению матрицы А
на множители:
(5.61)
где U =А (т - 1>- верхняя треугольная матрица.
Разложение (5.61) не является LИ-разложением матрицы А. Однако
прямой ход по-прежнему равносилен LИ-разложению, но уже не самой
166

168. § 5.7. Метод Гаусса и разложение матрицы на множители. Ш-разложение
матрицы А, а матрицы А , полученной из нее в результате соответст­
вующей перестановки строк. Это разложение имеет вид
A=LU, (5.62)
- -где А =Рт_ 1Рт- 2 ... Р2 Р1 А, L - нижняя треугольная матрица, отли-
чающаяся от матрицы (5.57) перестановкой множителей в столбцах.
Пр им ер 5.14. Найдем разложение вида (5.62) для матрицы сис­
темы (5.39), используя результаты вычислений примера 5.9. Так как 1-й
шаг прямого хода не потребовал перестановки, а на 2-м шаге были
переставлены второе и третье уравнения, то
[
1 о 01 [ 1 о 01Р1 = О 1 О , Р2 = О О 1 ,
о о 1 о 1 о
[
2 -9 51
А= 1 -1 -7.5 ·
1.2 -5.3999 6
Для матрицы А прямой ход уже проводится по схеме единствен­
ного деления. Отличие от вычислений примера 5.9 состоит в том, что
на 2-м шаге множители µ 21 и µ 31 , а также второе и третье уравнения
системы (5.40) меняются местами. В результате получим разложение
вида (5.62), где
i = r~.50.6
01 [2 -9 5 11 О , U= О 3.5 -10 · "°
2.9. 10-5 1 о о 3.00029
о
После получения разложения вида (5.62) для решения системы Ах= Ь
выполняют следующие действия.
1°. Правую часть перестановкой элементов приводят к виду
Ь=Рт-lрт-2 ... Р2Р1Ь.
2°. Преобразуют вектор Ь по формулам прямого хода; необходи­
мые для вычислений множители µ,, берут из матрицы i. В результате
получают вектор ь<т - lJ.
3°. Обратной подстановкой решают систему Ux = ь<т - 1>.
Заметим, что матрица перестановки Pk полностью определяется
заданием номера ik уравнения, которое переставляется с k-м уравне­
нием. Поэтому для хранения всей информации о перестановках доста­
точно целочисленного массива длины т - 1.
167

169. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Пр им ер 5.15. Решим систему (5.39), использовав полученное
в примере 5.14 разложение матрицы А.
Здесь вектор Ь = (-4, 0.6001, -8.5)r преобразуется в вектор Ь
= (- 4, -8.5, 0.6001 )r перестановкой второго и третьего элементов.
Прямой ход.
- (1) - - - (1) - - -
1-и шаг. Ь2 =Ь 2 -µ21 Ь 1 =-8.5-0.5(-4)=-6.5, Ь3 =Ь 3 -µ31 Ь 1
= 0.6001 - 0.6 · (-4) = 3.0001. В результате l-го шага имеем ь< 1 >
= (-4, -6.5, 3.ОООl)Т.
2-й шаг. b~2 )=b~1 )-ji32b~1 ) = 3.0001 - 2.9· l0-5 ·(-6.5)"' 3.00029.
В результате прямого хода правая часть оказалась приведенной к виду
ь(2) = (-4, -6.5, 3.ооо29)Т.
Обратный ход проводится точно так же, как в примере 5.9, и дает
значения х3 = 1, х2 = 1, х1 =О. А.
§ 5.8. Метод Хопецкого (метод квадратных корней)
1. Описание метода. Пусть требуется решить систему линейных
алгебраических уравнений
Ах=Ь (5.63)
с симметричной положительно определенной матрицей А. Системы
уравнений такого типа часто встречаются в приложениях (например,
в задачах оптимизации, при решении уравнений математической
физики и др.). Для их решения весьма часто применяется метод Холец­
кого1 (другое название - метод квадратных корней)2.
В основе метода лежит алгоритм построения специального LU-раз­
ложения матрицы А, в результате чего она приводится к виду
А= LLТ. (5.64)
В разложении Холецкого (5.64) нижняя треугольная матрица
(5.65)
1 Андре-Луи Холецкиii (1875-1918) - французскнй математик и геодезист, лейте­
нант артиллерии. Погиб во время Первой мировой войны.
2 Идея метода была опубликована Гауссом в 1806 г.
168

170. § 5.8. Метод Холецкого (метод квадратных корней)
уже не обязательно должна иметь на главной диагонали единицы, как
это было в методе Гаусса, а требуется только, чтобы диагональные эле­
менты l;; были положительными.
Если разложение (5.64) получено, то решение системы (5.63) сво­
дится к последовательному решению двух систем с треугольными мат­
рицами:
Ly = Ь, LTx =у. (5.66)
Для решения систем (5.66) требуется выполнение примерно 2т2
арифметических операций.
Найдем элементы матрицы L. Для этого вычислим элементы мат­
рицы LLT и приравняем их соответствующим элементам матрицы А. В
результате получим систему уравнений
2
l11=a11;
1;1111 =ail, i=2,3, ...,m;
~1 +1;2 =0 22;
1;1/21 +1;2122 =а;2, i =3, 4, ..., т;
(5.67)
.2 2 2
1k1 + lk2 + ··· + lkk = akk;
1;1lk1 +l;zlk2+ ... +l;klkk=a;k• i=k+ l, ...,т;
2 2 2
/ml +lm2+ ··· +/тт=атт·
Решая систему (5.67), последовательно находим
111 =~;
lil=a;11111 , i=2,3, ...,m;
/22 = Jа22 - z;I;
1;2 =(а;2 - 1;1/ 21 )//22 , i =3, 4, ..., т; (5.68)
/kk = Jakk- IZ1 -IZ2- ... -IZ,k-1;
l;k=(a;k-lillk1 -l;2lk2- ... -/i.k-llk.k-1)!/kk, i=k+ l, ...,т;
169

171. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Заметим, что для вычисления диагональных элементов используется
операция извлечения квадратноm корня. Поэтому метод Холецкого
называют еще и методом квадратных корней. Доказано, что положи­
тельность соответствующих подкоренных выражений является следст­
вием положительной определенности матрицы А.
Замечание. Как следует из формул (5.68), матрица L, входящая
в разложение Холецкого (5.64), определяется по матрице А одно­
значно.
2. Достоинства метода. Метод Холецкоm обладает рядом ценных
качеств, которые позволяют предпочесть его методу Гаусса, если тре­
буется решить систему линейных алгебраических уравнений с симмет­
ричной и положительно определенной матрицей.
Как нетрудно подсчитать, число операций, выполняемых в ходе
вычисления разложения (5.64) по формулам (5.68), равно примерно
т3!3. Учитывая, что для решения систем (5.66) требуется примерно 2т2
арифметических операций, убеждаемся, что при больших т метод
Холецкого требует вдвое меньше вычислительных затрат по сравнению
с методом Гаусса.
Учет симметричности матрицы А позволяет экономно использовать
память компьютера при записи исходных данных задачи и результатов
вычислений. Действительно, для задания матрицы А достаточно ввести
в память компьютера только элементы alJ (1 ~ J), расположенные на
главной диагонали и под ней. В формулах (5.68) каждый такой элемент
alJ используется лишь однажды для получения 1,1 и далее в вычислениях
не участвует. Поэтому в процессе вычислений найденные элементы 1,1
могут последовательно замещать элементы а ,1 .
В результате нижняя треугольная матрица L может быть располо­
жена в той области памяти, где первоначально хранилась нижняя тре­
угольная часть матрицы А. Применение для решения системы (5.63)
метода Гаусса потребовало бы использования примерно вдвое боль­
шего объема памяти.
Безусловным достоинством метода Холецкого является также em
гарантированная устойчивость.
Пр им ер 5.16. Использовав метод Холецкого, найдем решение сис­
темы уравнений с симметричной положительно определенной матрицей:
170
6.25х 1 -
-XI +
х2 + О.5х3 = 7.5,
5х2 + 2.12х3 = -8.68,
О.5х 1 + 2.12х2 + 3.6х3 = -0.24.

172. § 5.9. Метод прогонки
По формулам (5.68) последовательно находим:
/11 = Ji;'i = J6.25 = 2.5, /21 = а21 //11 = -1/2.5 = -0.4;
/31 = а31 //11 = 0.512.5 = 0.2, /22 = Ja22 -1;1= J5-0.16 = 2.2;
132 = (а32 - /31121 )//22 = (2.12 - 0.2(-0.4))/2.2 = !;
133=Ja33 -/;1 -/;2 =JЗ.6-0.22 -1 2 =1.6.
Следовательно, матрица L такова:
L = -0.4 2.2 О ·l2.5 о о ]
0.2 1 1.6
Система Ly = Ь имеет вид
2.5у, = 7.5,
-О.4у1 + 2.2у2 = -8.68,
О.2у1 + у2 + 1.6у3 = -0.24.
Решая ее, получаем у1 = 3, у2 = -3.4, у3 = 1.6.
Далее из системы Lтх =у, которая имеет вид
2.5х 1 - О.4х2 + О.2х3 = 3,
2.2Х2 + Х3 = -3.4,
1.6Х3 = 1.6,
находим решение х 1 = 0.8, х2 = -2, х3 = 1. А
§ 5.9. Метод прогонки
Рассмотрим метод прогонки 1 - простой и эффективный алгоритм
решения систем линейных алгебраических уравнений с трехдиагональ­
ными матрицами
Ь1Х1 + С1Х2
a-r1 + br2 + c-r3
й;Х; - 1 + Ь;Х; + С;Х; + 1 =d,,
ат - 1Хт - 2 + Ьт - 1Хт - 1 + Ст - Хт = dm - !•
йmХт - 1 + ЬтХт = dm.
(5.69)
1 Метод прогонки был предложен в начале 50-х годов независимо несколькими авто­
рами, в том числе российскими учеными И.М. Гельфандом, О.В. Локуцневскнм, В.С. Вла­
димировым, АС. Кронродом.
171

173. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Системы такого вида часто возникают при решении различных
задач математической физики, а также при решении других вычисли­
тельных задач (например, приближения функций сплайнами).
1. Вывод расчетных формул. Преобразуем первое уравнение сис­
темы (5.69) к виду
(5.70)
где а 1 = -с/Ь 1 , /31 = d/b1•
Подставим полученное для х1 выражение во второе уравнение сис­
темы:
aia1X2 + /31) + br2 + Cr3 = d2.
Преобразуем это уравнение к виду
Х2 = а2хз + /32, (5.71)
где а2 = -с2 /(Ь2 + а2а 1 ), /32 = (d2 - a2j31)/(b2 + а2а 1 ).
Выражение (5.71) подставляем в третье уравнение системы и т.д.
На i-м шаге этого процесса (1 < i < т) i-e уравнение системы преоб-
разуется к виду
(5.72)
где а;= -c;l(b; + а;а;_ 1), /3; = (dг а;/3;_ 1)/(Ь; + а;а;_ 1).
На т-м шаге подстановка в последнее уравнение выраженияхт _ 1 =
= ат - 1Хт + 13т - 1 дает:
0т(ат - 1Хт + 13т- 1) + Ьтхт = dm.
Откуда можно определить значение х т:
хт = 13т = (dm - 0т/3т - 1)/(Ьт + атат- 1)·
Значения остальных неизвестных х; для i = т - 1, т - 2, ..., l теперь
легко вычисляются по формуле (5.72).
2. Алгоритм прогонки. Сделанные преобразования позволяют
организовать вычисления метода прогонки в два этапа.
Прямой ход метода прогонки (прямая прогонка) состоит в вычисле­
нии прогоночных коэффициентов а; (l $ i < т) и /3; (l $ i $ т). При
i = l кюффициенты вычисляют по формулам
а 1 = --с1 /у1 , /31 = d1/y1• у 1 = Ь 1 , (5.73)
а при i = 2, 3, ..., т - 1 - по рекуррентным формулам
(5.74)
172

174. § 5.9. Метод прогонки
При i = т прямая прогонка завершается вычислением
Рт= (dm - атРт- 1)/ут, Ут = Ьт + атат - 1• (5.75)
Обратный ход метода прогонки (обратная прогонка), дает значения
неизвестных. Сначала полагают хт = Рт· Затем значения остальных
неизвестных вычисляют по формуле
х;=а;Х;+ 1 +р;, i=m-l,m-2, ...,l. (5.76)
Вычисления ведут в порядке убывания значений i от т - 1 до 1.
Пример 5.17. Использовав метод прогонки, решим систему
5xl - Х2 = 2.0,
2х 1 + 4.6х2 - х3 = 3.3,
2х2 + 3.6х3 - О.8х4 = 2.6,
3х3 + 4.4х4 = 7.2.
Прямой ход. Согласно формулам (5.73Н5.75) получаем:
у1 = Ь 1 = 5, а1 = -с 1/у 1 = 1/5 = 0.2, 1}1 = d1/y1 = 2.0/5 = 0.4;
у2 = Ь2 + а2а 1 = 4.6 + 2 · 0.2 = 5, а2 = -с2 1у2 = 1/5 = 0.2;
Р2 = (d2 - а2/} 1 )/у2 = (3.3 - 2 · 0.4)/5 = 0.5;
Уз= Ь3 + а3а2 = 3.6 +2 •0.2 = 4, а3 = -с3 /у3 = 0.8/4 =0.2;
Рз =(d3 - а3Р2)/у3 = (2.6 - 2 •0.5)/4 = 0.4;
у4 = Ь4 + а4а3 =4.4 + 3 •0.2 = 5;
Р4 =(d4 - а4Р3)/у4 =(7.2 - 3 •0.4)/5 = 1.2.
Обратный ход. Полагаем х4 =1}4 = 1.2. Далее находим:
х3 =а3 х4 + Рз =0.2 • 1.2 + 0.4 =0.64;
Х2 =С12Х3 + Р2 = 0.2. 0.64 + 0.5 =0.628;
Х1 = С11Х2 + Р1 =0.2. 0.628 + 0.4 = 0.5256.
Итак, получаем решение:
Х1 = 0.5256, Х2 = 0.628, Х3 = 0.64, Х4 = .2....
3. Свойства метода прогонки. Непосредственный подсчет показы­
вает, что для реализации вычислений по формулам (5.73Н5.76) тре­
буется примерно 8т арифметических операций, тогда как в методе
Гаусса это число составляет примерно (2/З)т3 . Важно и то, что трех­
диагональная структура матрицы системы позволяет использовать для
ее хранения лишь Зт - 2 машинных слова.
Таким образом, при одной и той же производительности и оператив­
ной памяти компьютера метод прогонки позволяет решать системы
173

175. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
гораздо большей размерности, чем стандартный метод Гаусса для сис­
тем уравнений с заполненной матрицей.
Приведем простые достаточные условия на коэффициенты системы
(5.69), при выполнении которых вычисления по формулам прямой про­
гонки могут быть доведены до конца (ни один из знаменателей у1 не
обратится в нуль). В частности, это гарантирует существование реше­
ния системы (5.69) и его единственность. При выполнении тех же
условий коэффициенты а, при всех 1 удовлетворяют неравенству а, S
S 1, а следовательно, обратная прогонка по формуле (5.76) устойчива
по входным данным (см. пример 3.27). Положим а 1 =О, ст= О.
Теорема 5.4. Пусть коэффициенты системы (5.69) удовлетво­
ряют следующим условиям диагонального преобладания:
bkl ~ ak + ck, bk > ak (1 SkSт). (5.77)
Тогда у1 *О и а, S 1 для всех i = 1, 2, ..., т.
До к аз ат ель ст в о. Воспользуемся принципом математической
индукции. Из условий теоремы имеем у1 = Ь1 *О и а1 = с1 / Ь1 S 1.
Пусть теперь yk _1 *О и 1ak _11 S 1 для некоторого k > 1. Тогда
Из полученной оценки в силу условий (5.77) вытекает справедли­
вость неравенств yk >Ои yk ~ сk.Следовательно,уk*Ои ak
= cklyk $ 1.•
4. Метод прогонки и разложение матрицы на множители. Опи­
санный вариант метода прогонки можно рассматривать как одну из
схем метода Гаусса (без выбора главного элемента), в результате пря-
мого хода которого исходная трехдиагональная матрица
Ь1 CI о о ... о о о
а2 Ь2 С2 о ... о о о
А=
о аз Ьз С3 ... о о о
.............................
о о о о ··· ат-1 ьт-1 ст-1
о о о о ... о ат ьт
представляется в виде произведения двух двухдиагональных матриц:
A=LU. (5.78)
174

176. § 5.9. Метод прогонки
Здесь
У1 о о ." о о 1 -а1 о ". о о
а2 У2 о ".о о о -а2 ". о о
L= о а3 Уз ." о о U=
о о о 1 -am-1
о о о ".ат Ут о о о о
Так как для определения L и U нет необходимости вычислять коэф­
фициенты Р,, то общее число операций на получение разложения (5.78)
составляет примерно Зт.
Подобно тому как это описано в § 5.7, разложение (5.78) можно
использовать для решения систем с многими правыми частями. Если
нужно решить р систем с матрицей А, то общее число операций соста­
вит примерно Зт + 5тр.
К сожалению, при обращении матрицы А теряется ее трехдиаго­
нальная структура. Обратная матрица является заполненной, однако
для ее вычисления с помощью разложения (5.78) требуется примерно
лишь 2.5 т2 арифметических операций.
Так как det А = det L · det U, а det U = l, то определитель трехдиаго­
нальной матрицы, после того как получено разложение (5.78), вычисля­
ется по элементарной формуле
5. Некоторые варианты метода прогонки. Наряду с изложенным
выше «стандартным)) вариантом метода прогонки (правой прогонкой)
существует большое число других вариантов этого метода. Это методы
левой прогонки, встречных прогонок, немонотонной прогонки, потоко­
вый вариант метода прогонки. В ряде случаев эти модификации могут
существенно улучшить обусловленность прогонки.
Для систем уравнений, обладающих близкой к (5.69) структуре, раз­
работаны методы циклической прогонки, матричной прогонки и др.
С указанными вариантами метода прогонки можно подробно озна­
комиться в [50, 89].
175

177. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
§ 5.10. QR-разnожение матрицы.
Методы вращений и отражений
Метод Гаусса не является единственным методом исключения,
используемым для решения систем линейных уравнений и приведения
матриц к треугольному виду. Рассмотрим два метода исключения, обла­
дающих в отличие от метода Гаусса гарантированной хорошей обуслов­
ленностью - метод вращений и метод отражений. Оба этих метода
позволяют получить представление исходной матрицы А в виде произве­
дения ортогональной 1 матрицы Q на верхнюю треугольную матрицу R:
A=QR. (5.79)
Представление (5 79) - это QR-разложение матрицы на множители
1. Метод вращений. Опишем прямой ход метода. На 1-м шаге
неизвестное х 1 исключают из всех уравнений, кроме первого. Для
исключения х 1 из второго уравнения вычисляют числа
(5.80)
обладающие следующими свойствами:
2 2
С12 +S12 = , -S12011 + С12021 =0. (5.81)
Затем первое уравнение системы заменяют линейной комбинацией пер­
вого и второго уравнений с коэффициентами с12 и s12, а второе уравне­
ние - аналогичной линейной комбинацией с коэффициентами -s12 и с 12.
В результате получают систему
(1) ( 1) ( 1)
+ 0< 1 >х = ь< 1 >011 Х1 + 012 Х2 + О13 Х3 + '"' т 1 •
() ()
+ а11 >х = ь0 >0 22 Х2 + О23 Х3 + 2т т 2 •
О31Х1 + О32Х2 + О33Х3 + + о3,,,х,,, = Ьз'
(5.82)
1 Напомним, что веwественнu матрица Q называется ортогональноli, если для нее
выполнено условие QT = Q-•, что эквивалентно равенствам QTQ = QQT= Е. Важное своli­
ство ортогонш~ьного прео6разо11ания векторов (т.е. преобраэованИJJ векторов с помощью их
умножения на ортогональную матрицу Q), состоит в том, что это преобразование не
'llеняет евклидову норму векторов 11Qx112 = llxll2 для всех х Е JRm.
176

178. § 5.10. ОR-разложение матрицы. Методы вращений и отражений
в которой
( 1) (1)
о,1 =c,2011+s,2021• 021 =-s,2011+c12021• (ls;Js;m);
Ь1>=с,2Ь1 +s12b2, b~1J=-s,2b1 +с12Ь2
(5.83)
Заметим, что о~> = -s12o11 + с12о21 =О в силу специального выбора
чисел с 12 и s12 (см. (5.81)).
Естественно, что если 0 21 = О, исходная система уже имеет вид
(5.82) и в исключении неизвестного х 1 из второго уравнения нет необ­
ходимости В этом случае полагают с 12 = 1 и s12 =О.
Как нетрудно видеть, преобразование исходной системы (5.) к виду
(5.82) эквивалентно умножению слева матрицы А и правой части Ь на
матрицу Т12, имеющую вид
С12 S12 о о .. о
-s,2 С12 о о ... о
Т12= о о о ... о
о о о 1 ... о
о о о о ". 1
Дrtя исключения неизвестногох1 из третьего уравнения вычисляют числа
(1)
all
с 13 =-;::::====
(а1>2 +а;,
(5.84)
2 2 (1)
такие, что с 13 + s 13 1, -s13o11 + с 13 о31 "'О. Затем первое уравнение
системы (5.82) заменяют линейной комбинацией первого и третьего
уравнений с коэффициентами с 13 и s13, а третье уравнение - аналогич-
ной комбинацией с коэффициентами -s13 и с 13. Это преобразование
системы эквивалентно умножению слева на матрицу
177

179. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
С13 о 5 13 о о
о 1 о о о
Т13 = -S13 о С13 о ... о
о о о 1 ... о
.................
о о о о ... 1
и приводит к тому, что коэффициент при х1 в преобразованном третьем
уравнении обращается в нуль.
Таким же образом х1 исключают из уравнений с номерами i = 4, ..., т.
В результате 1-го шага (состоящего, как мы видели, из т - 1 «малых))
шагов) система приводится к виду
(m-1) (m-1)
+ 0 12 Х2 + О13 Х3 +
+ (m-1) - ь<т-1)
0 1т Хт - 1 •
(1) ( 1)
022 Xz + 023 Х3 + ... + о0 >х = ь< 1 >2т т 2 •
( 1) ( 1)
О32 Х2 + О33 Х3 + ··· +
(S.8S)
от(13)х3 + ... + o(I) х = ь< 1 >тт т т.
В матричной записи получаем:
АО>х = ьо>,
где А <1> = Т1т ... Т13 Т12А, b(I) = Т1т ..• Т13 Т12Ь.
Здесь и далее через Tkl обозначена матрица элементарного преобра­
зования, отличающаяся от единичной матрицы Е только четырьмя эле­
ментами. В ней элементы с индексами (k, k) и (/, [) равны ckl, элемент
с индексами (k, [)равен skl• а элемент с индексами(/, k) равен-sk/• при­
чем выполнено условие
(5.86)
Действие матрицы Tk1 на вектор х эквивалентно его повороту вокруг
оси, перпендикулярной плоскости Oxkx1 на угол Pk/ такой, что ckl =
=cos PkJ• skl = SIП(f)н (существование такого угла гарантируется равен­
ством (5.86)). Эта геометрическая интерпретация и дала название
методу вращений. Операцию умножения на матрицу Tkl часто назы-
178

180. § 5.10. QR-разложение матрицы. Методы вращений и отражений
вают плоским вращением (или преобразованием Гивенса). Заметим, что
т -1
Tkz = Tk1 и, следовательно, матрица Tk1ортогональная.
На 2-м шаге метода вращений, состоящем из т - 2 «малых» шагов,
из уравнений системы (5.85) с номерами / = 3, 4, "" т исключают неиз­
вестное х2• Для этого каждое 1-е уравнение комбинируют со вторым
уравнением. В результате приходим к системе
(m-1) (m-1) (m-1) (m-1) _ (m-1)
а11 Х1 + а12 Х2 + а13 Х3 + ". + alm Хт - Ь1 •
(m-1) (m-1)
а22 Х2 + а23 Х3 +
(m-1) (m-1)
... + а2т Хт = Ь2 '
(2)
а33 Х3 + + а(2)х = ь<2)
". 3т т 3 •
а<2 >х + + а<2 >х = ь<2>т3 3 ". тт т т ·
В матричной форме записи получаем
А(2)х = Ь(2),
гдеА<2> = Т2т ". T24T23 A(I>, Ь(2) = Т2т ". T24T23 b<I).
После завершения (m - 1)-го шага система принимает вид
(т - 1) (m - 1) (m - 1) (m - 1) (m - 1)
а11 Х1 + а12 Х2 + а13 Х3 + ". + alm Хт = Ь1 •
(m-1) (m-1) (m-1) _ (m-1)
а22 Х2 + а23 Х3 + "· + а2т Хт - Ь2 •
(т - 1) (m - 1) _ (т - 1)
а33 Х3 + "· + а3т Хт - Ь3 •
(m-1) - ь<т-1)
атт Хт - т •
или в матричной форме записи
л<т- l)x = ь<т- 1),
гдеА<m-1) = Т л<т-2) ь<т-1) = Т ь<т-2)_
т - 1, т ' т - 1, т
Введем обозначение R для полученной верхней треугольной мат­
рицы А (т - 1). Она связана с исходной матрицей А равенством
R=TA,
где Т= Tm- I, т ". Т2т ". Т23 Т1 т ". Т13 Т12 - матрица результирующего
вращения. Заметим, что матрица Т ортогональна как произведение
ортогональных матриц. Обозначая Q = т- 1 = ТТ, получаем QR-разложе­
ние матрицы А.
179

181. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Обратный ход метода вращений проводится точно так же, как и для
метода Гаусса.
Метод вращений обладает замечательной численной устойчивостью.
Для него оценка (5.43) справедлива с коэффициентом /(т} = 6т.
Однако этот метод существенно более трудоемок по сравнению с мето­
дом Гаусса. Получение QR-разложения для квадратной матрицы А
общего вида требует примерно 2т3 арифметических операций.
Пр им ер 5.18. Использовав метод вращений, решим на 6-разряд­
ном десятичном компьютере систему уравнений
2х 1 - 9х2 + 5х3 = -4,
1.2х 1 - 5.3999х2 + 6х3 = 0.6001,
Прямой ход.
1-й шаг. Исключим х 1 из второго уравнения. Для этого вычислим
с12 и s12 по формулам (5.80):
St2 1·2 =0.514495.
J22+ 1.22
Преобразуя коэффициенты первого и второго уравнений по форму­
лам (5.83), приходим к системе
2.33238х1 - 10.4957х2 + 7.37444х3 = -3.12122,
7.85493 • I0-5x2 + 2.57248х3 = 2.57256,
7.5х3 = -8.5.
Далее вычислим коэффициенты с 13 и s13 по формулам (5.84):
2.33238 1
С13 = 0.919087, S13 = 0.394055.
J2.з323s2 + 12 J2.3323s2 + 12
Заменяя первое и третье уравнения их линейными комбинациями
с коэффициентами с13, s13 и -s13, с13 соответственно, получаем систему
2.53772х 1 -
180
10.0405х2 + 3.82234х3 = -6.21814,
7.85493 • I0-5x2 + 2.57248х3 = 2.57256,
3.21680х2 - 9.79909х3 = -6.58231.

182. § 5.10. QR-разложение матрицы. Методы вращений и отражений
2-й шаг. В полученной системе имеем а~;> = 7.85493 • 10-s, а~;>
=3.21680. Поэтому
( 1)
й22
С23= ::::2.44185 • I0-5 , S23"' 1.00000.
(а~;»2 + (а~~»2
Заменяя второе и третье уравнения системы их линейными комби­
нациями с коэффициентами с23, s23 и -s23, с23 соответственно, прихо-
дим к системе
2.53772х 1 - 10.0405х2 + 3.82234х3 = -6.21814,
3.21680х2 + 9.79903х3 = -6.58225,
- 2.57272х3 = -2.57272.
Обратный ход дает последовательно значения х3 = 1, х2 =
=0.999994, х 1 =-1.58579·10-s. .А.
2. Метод отражений. Матрицами Хаусхолдера (или отражений)
называются квадратные матрицы вида
V= E-2wwт,
где w - вектор-столбец в яm, имеющий единичную длину: llwll2 = 1.
Матрица Хаусхолдера симметрична и ортогональна. Действительно,
vт = (Е - 2wwT)T =вт - 2(wT)T wт = Е - 2wwт = V;
vтv = VV = (Е - 2wwT)(E - 2wwт) = Е - 4wwт + 4wwтwwT = Е.
Здесь учтено, что w7w = llwll; = 1.
Умножение на матрицу V называют преобразованием Хаусхолдера
(или отражением). Действие V на вектор х можно интерпретировать
как ортогональное отражение вектора в R"' относительно гиперплоско­
сти, проходящей через начало координат и имеющей нормальный век­
тор, равный w.
Как и вращения, отражения используются для обращения в нуль
элементов преобразуемой матрицы. Однако здесь с помощью одного
отражения можно обратить в нуль уже не один элемент матрицы, а
целую группу элементов некоторого столбца или строки. Поэтому,
являясь почти столь же устойчивым, как и метод вращений, метод
отражений позволяет получить QR-разложение квадратной матрицы
общего вида примерно за (4/З)т3 арифметических операций, т.е. в пол­
тора раза быстрее. Изложение самого метода можно найти, например,
в [9).
181

183. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Поясним, как получается QR-разложение матрицы А с помощью
преобразований Хаусхолдера. Пусть а = (а1 , а2, "" ат)т - произволь­
ный вектор, у которого одна координат а2, ", ат отлична от нуля.
Покажем, что вектор w в преобразовании Хаусхолдера может быть
выбран так, чтобы обратились в нуль все координаты вектора Va кроме
первой: Va = се 1 =с(!, О, "" О)т. Поскольку ортогональное преобразо-
вание не меняет евклидову норму вектора, то с = llall2 и искомое пре­
образование таково, что
Va = (Е - 2wwT)a =а - 2(w, a)w =а - aw = llall2e1 ,
где а= 2(w, а). Таким образом, вектор w следует выбрать так, чтобы
aw1 - а1 = ±llall2 , aw2 = а2, "" аwт =ат,
что эквивалентно равенству w = а-1 (а ± lla/12e1 ). Вспоминая, что а =
= 2(w, а) = 2(w1a 1 + w2a2 + ". + wтат), имеем
v
Таким образом w = llvll2
, где v =а± llall2e1 •
Взяв а= а 1, где а1 - первый из столбцов матрицы А, и положив Р1 = V,
получим
( 1)
а11
()
а,2
( 1)
013
( 1)
ат
о
( 1)
0 22
( 1)
аzз
( 1)
02т
A<1J = Р1 А =
о
( 1)
О32
( 1)
О33
( 1)
азт
..................
о
( 1)
ат2
( 1) ( 1)
ат3 ". атт
д ( (1) ( I >)т вт I обалее, взяв вектор а2 = а22 , .• " ат2 Е - , с помощью пре разо-
вания Хаусхолдера Vт _ 1 в пространстве (т - l)-мерных векторов можно
обнулить все координэ:rы вектора Vт _ 1а2 кроме первой. Положив
P=(l О)
2 о vm- l '
182

184. § 5.10. QR-разложение матрицы. Методы вращений и отражений
получим:
(1)
0 11
(1)
0 12
(1)
0 13
(1)
0 1т
о
(2)
022
(2)
0 23
(2)
02т
А (2) = P:zA (J} =Р2Р1А =
о о
(2)
0 23
(2)
02т
о о
(2) (2)
0т3 ". 0тт
Заметим, что первый столбец и первая строка матрицы при этом
преобразовании не меняется.
Выполнив т - 1 шаг этого метода, приходим к верхней треугольной
матрице
(1)
0 11
(1)
0 12
(1)
0 13
(1)
0 1т
о
(2)
0 22
(2)
0 23
(2)
02т
А (111- J> =рт - 1 ". Р2Р1А =
о о
(3)
О33
(3)
03т
о о
(т-1)
О ". отт
Поскольку матрицы Р1, "., Рт_ 1 симметричны и ортогональны,
получено разложение
A=QR,
где матрица Q= Р1Р2 ".Рт- 1 - ортогональная, а матрица R =А (т-1) _
верхняя треугольная.
Пример 5.19. Применим метод отражений для решения системы
уравнений из примера 5.18
2х 1 - 9х2 + 5х3 = -4,
1.2х 1 - 5.3999х2 + 6х3 = 0.6001,
Х1 - Х2 - 7.5Х3 = -8.5.
Прямой ход. Возьмем первый столбец матрицы системы а 1 -=
= (2, 1.2, l)т, положим v = а 1 + lla1ll2e1 = (2 + J6.44, 1.2, 1/ ""
""(4.53772, 1.2, l)r и выберем
w = vl llvll2 ""(0.945545, 0.250049, 0.208375)7:
183

185. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Построим матрицу Хаусхолдера
V=E-2wwT=
[
1 о
= о 1
о о
о] [О.945545]о - 2 0.250049 (о 945545 о 250049
1 0.208375
0.208375) ::::
о о] [ о.894055 о.236433 0.197028 ]
l о - 2 0.236433 0.0625245 0.0521040 ""
о 1 0.197028 0.0521040 0.0434201
[
-0.788110 -0.472866 -0.394056]
:::: -0.472866 0.874951 -0.104208 .
-0.394056 -0.104208 О.913160
Применим к левой и правой частям системы преобразование Хаус­
холдера и получим эквивалентную систему
-2.53772х 1 + 10.0405х2 + 3.82233х3 = 6.21815,
- О.364646х2 + 3.66694х3 = 3.30229,
3.19606х2 - 9.44423х3 = -6.24817.
Возьмем теперь а2 = (--Q.364646, 3.l9606)r и построим двумерное
преобразование Хаусхолдера. Здесь уже v = а2 + lla211 2(l, О)Т =
= <-о.364646 + Jo.3646462 + 3.196062, 3.19606{ "" (2.85215, 3 19606)
w= v/llvl/2 ::= (0.665824, 0.746109)7: Двумерная матрица Хаусхолдера
имеет вид
v = r1 ol _J0.6658240665824,0.746109):::: [ 0.113357 -0.993555l.
2 lo 1J lo.746109J -О.993555 -O.ll3357j
Умножив обе части системы на матрицу
о о J0.113357 -0.993555 '
-0.993555 -0.113357
184

186. § 5.11. Итерационное уточнение
получим
-2.53772х 1 + 10.0405х2 - З 82233х3 = 6.21815,
- З.21680х2 + 9.79904х3 = 6.58224,
- 2.57274х3 = -2.57273.
Обратный ход последовательно дает значения х3 :::: 0.999996, х2 ::::
:::: 0.999988, х 1 :::: -3.35721 • I0-5. .А,
§ 5.11. Итерационное уточнение
В большинстве случаев метод Гаусса с выбором главного элемента
позволяет получить приближенное решение с довольно высокой точно­
стью. Однако иногда возникает необходимость найти решение с боль­
шей точностью. Полезно знать, что существует метод, позволяющий
найти приближенное решение с относительной точностью, сравнимой
с &м, если только число обусловленности не слишком велико. Этот
метод, называемый итерационным уточнением, требует небольшого
(примерно на 25 %) увеличения машинного времени по сравнению с
затратами на получение решения методом Гаусса.
Пусть х<0> - найденное на компьютере приближенное решение сис­
темы Ах = Ь. Напомним (см. § 5.1), что невязка r<0> = Ь - Ах<0> и
погрешность е<0> = х - х<0> связаны равенством
Ае<0> = r<0>. (5.87)
Если бы удалось найти е<0> как точное решение системы (5.87). то
векторхО> =х(О) + е<0> дал бы точное решение системы Ах= Ь. Однако в
действительности вычисленное на компьютере значение х< 1 > неизбежно
будет содержать погрешность. Тем не менее можно ожидать, что х< 1 >
окажется лучшим приближением, чем х<0>. Использовав приближение
хО >, аналогичным образом можно найти приближение х12)_
Опишем более подробно очередной (k + 1)-й шаг метода.
1°. Вычисляют r<k> :::: Ь - Ax<k>. Исключительно важно, чтобы
вычисление r(k) производилось с повышенной точностью. Дело в том,
что Ь :::: Ax(k) и поэтому при вычислении невязки неизбежно вычитание
близких чисел, а следовательно, потеря большого числа значащих
цифр. Одна из возможностей состоит в использовании для вычисления
Ax<k> и Ь - Ax<k> арифметики удвоенной точности.
2° Вычисляют решение системы Ae<k> = r(k). Так как матрица А не
меняется, то получение очередного приближения с использованием
185

187. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
однажды вычисленного LU-разложения матрицы А (с учетом необходи­
мых перестановок строк) требует сравнительно небольшого числа
(примерно т2 ) арифметических действий.
3°. Вычисляют x<k + 1> "'x<k) + e<k).
Если число обусловленности не очень велико (например,
-1
cond (А) « Ем , то метод довольно быстро сходится. Сходимость харак-
теризуется постепенным установлением значащих цифр в приближениях
~k)_ Если же процесс расходится, то в приближениях не устанавлива­
ются даже старшие значащие цифры.
3 а меч ан и е. Итерационное уточнение не следует рассматривать
как средство, позволяющее справиться с плохой обусловленностью
системы. Ero применение для решения плохо обусловленных систем
целесообразно только, если матрица А и вектор правых частей Ь
в компьютере заданы точно или с повышенной точностью.
Необходимо отметить одну интересную особенность. В процессе
итерационного уточнения невязки ,щ обычно не уменьшаются, а даже
несколько возрастают по величине.
Кроме тоrо, как оказывается, приближения x(k) могут быть использо­
ваны для грубого по порядку оценивания естественного числа обуслов­
ленности v0(x). Для этого достаточно воспользоваться приближенной
формулой
(5.88)
Пр им ер S.20. Используя алrоритм итерационного уточнения, най­
дем решение системы
1.03х 1 + 0.99lx2 = 2.51,
0.99lx1 + О.94Зх2 = 2.41
(5.89)
на 3-разрядном десятичном компьютере, считая, что режим вычисле­
ний с удвоенной точностью на нем эквивалентен использованию 6-раз­
рядноrо десятичного компьютера.
Вычислим множитель первого (и в данном случае последнего) шага
прямоrо хода метода Гаусса: µ = 0.991/1.03 "'0.962. Так как при вычис­
лении на 3-разрядном компьютере имеем 0.943 - 0.991 · 0.962 "' -0.01
и 2.41 - 2.51 · О. 962 "' О, то второе уравнение системы (5.89) приводится
к виду -O.Olx2 =О.
186

188. § 5.11. Итерационное уточнение
Обратная подстановка дает приближенное решение х0> 2.44,
х~О) = 0.
Итерационное уточнение.
1- й шаг. Вычислим (с удвоенной точностью) компоненты невязки:
r0> = 2.5 l - 1.03х0> - 0.99lxi0> = -0.00320,
r~O) = 2.41 - 0.991х0> - 0.943xi0> = -0.00840.
Вычислив методом Гаусса решение системы
1.03е0> + 0.99lei0> = -0.00320,
О.991е0> + 0.943ei0> = -0.00840,
получим е0> = -0.481, ei0> = 0.496. Завершается 1-й шаг вычислением
х1 = х0> + е0>, х2 = xi0>+ ei0>, приводящим на 3-разрядном компьютере
к значениям х1 > = 1.96, xi1> = 0.496.
2-й шаг дает значения r1> = -0.000336, r~1 > = -0.000088, е1 >
- (!)_ (2)_ х<2>_
-0.0223, е2 - -0.0235 И Х1 - 1.98, 2 - 0.473.
3- й шаг дает значения r2> = 0.00186, ri2> 0.00178,
(2) (3) (3)
=0.00084, е2 = 0.001 и х 1 = l .98, х2 = 0.474.
Сравнивая х<2> и х(З), замечаем, что последние значащие цифры прак­
тически установились и, следовательно, процесс следует завершить,
приняв х 1 ""' 1.98, х2 ""' 0.474.
Использование формулы (5.88) с Ем = 5 · l0-4 дает следующую
оценку естественного числа обусловленности:
v0 (x)""' E~1 lle<0>llcx,!llx<0>iloo ""'2 · 103 • 0.496/2.44 ""'409.
Приведем для сравнения действительные значения решения и есте­
ственного числа обусловленности: х 1 ""' l.9812, х2 ""'0.4735, v0(x)""' 273
(см. пример 5.5). А
187

189. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
§ 5. 12. Линейная задача метода наименьших квадратов
1. Линейная задача метода наименьших квадратов и переопреде­
ленные системы. Метод наименьших квадратов широко используется
в самых разных предметных областях при обработке эксперименталь­
ных данных. В статистике этот метод принято называть линейной рег­
рессией. Инженеры приходят к нему, занимаясь оцениванием парамет­
ров или фильтрацией. Мы встретимся с методом наименьших
квадратов в гл. 11 при изучении методов приближения таблично задан­
ных функций. Автором метода является Гаусс, который изобрел его в
1795 г. при решении поставленной перед ним немецким правитель­
ством задачи обновления координат землемерных вех из государ­
ственной базы данных.
Независимо от того, для решения какой прикладной задачи исполь­
зуется метод наименьших квадратов, в плане вычислений он сводится к
следующей ключевой задаче, которую принято называть линейной зада­
чей метода наименьших квадратов. Пусть А - прямоугольная матрица
размера пхт с элементами alJ, а Ь е JRn - заданный вектор. Требуется
найти вектор х е JRm, минимизирующий величину l!Ax- bll2 , т.е.
такой вектор х , что
11Ax-Ыl 2 =min 11Ax-bll2 • (5.90)
хе Rm
Линейная задача метода наименьших квадратов естественным обра­
зом возникает и при решении систем линейных алгебраических уравне­
ний. Предположим, что требуется решить систему п линейных алгебра­
ических уравнений с т неизвестными, где п > т
а11Х1 + а12Х2 +
а21Х1 + а22Х2 +
+ а1тХт = Ь1,
+ а1тХт = Ь2,
(5.91)
Системы уравнений (5.91 ), в которых число уравнений превышает
число неизвестных, называют переопределенны.тwи. Для переопределен­
ной системы, вообще говоря, нельзя найти вектор х, точно удовлетворя­
ющий уравнениям системы. Однако, хотя уравнения системы нельзя
удовлетворить точно, можно попытаться удовлетворить их как можно
точнее, минимизируя величину вектора невязки r = Ь - Ах. Выбор в
качестве минимизируемой величины евклидовой нормы невязки 11r112 =
188

190. § 5.12. Линейная задача метода наименьших квадратов
= /lb-Ax/1 2 приводит к методу наименьших квадратов решения пере­
определенных систем. Другими словами, в этом методе предлагается за
решение переопределенной системы принять решение х линейной
задачи метода наименьших квадратов, обладающее свойством (5.90).
2. Нормальная система метода наименьших квадратов. Простей­
шим подходом к решению линейной задачи метода наименьших квадра­
тов является использование нормальной системы метода наименьших
квадратов
(5.92)
Обоснованием такого подхода является следующий результат.
Теорема 5.5. Вектор х минимизирует величину llAx - Ь11 2 тогда и
только тогда, когда он является решением нормальной системы (5.92).
Доказательство. Для любых векторов х, х Е JRm имеем
Ах-Ь =Ах -Ь+ А(х- х).
Оrсюда
llAx-bll; = llAx -bll; + 2(Ах -Ь, А(х- х)) + i~(x- x)ll; =
= llAx -ь11; + 2(z, х- х) + l~(x- x)ll;,
где z=AT(Ax-b)=ATAx-Arb.
Если х удовлетворяет нормальной системе (5.92), то z =О и
/1Ах-ь11; = /1Ах-ь11; + l~<x- x)ll; ~ llAx -ь11;
для всехх Е JRm. Это означает, что х минимизирует /1Ax-bll2 .
Если же х не является решением нормальной системы (5.92), то z Ф О.
Возьмем х = х -&z и заметим, что
/1Ах-ь11;= /1Ax-ь11;-2&11zll;+&2 1/Azll;< llAx-ь11;
для всех достаточно малых & > О. Это означает, что х не обладает
свойством (5.90).•
Обратим внимание на то, что вектор Ах представляет собой линей­
ную комбинацию столбцов а 1 , а2, ••• ,ат матрицы А с коэффициентами
Хр Х2, ... , Хт:
189

191. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
т
Ах= ~:Х1а1 .
1=1
Таким образом, справедливо следующее утверждение.
Л ем м а 5.2. Столбцы матрицы А линейно зависимы тогда и
только тогда, когда существует ненулевой вектор х такой, что Ах = О.
Столбцы матрицы А линейно независимы тогда и только тогда, когда
Ах '!:- О для всех х '!:- О. •
Рассмотрим некоторые свойства матрицы АТА и нормальной сис­
темы (5.92). Заметим, что матрица АТА - квадратная размера тхт.
Лемм а 5.3. Матрица АТА - симметричная, причем
(АТАх, х) ~О Ух е JRm.
Если столбцы матрицы А линейно независимы, то матрица АТА
положительно определенная.
До к аз ат ель ст в о. Матрица симметрична, так как
(АТА)Т = АТ(АТ )Т = АТА.
Кроме того,
(АтАх, х) =(Ах, Ах)= llAxll; ~ О Ух е JRm. (5.93)
Если столбцы матрицы А линейно независимы, то в силу леммы 5.2
имеем Ах'!:- О для всех х '!:- О. Поэтому
(АтАх, х) = llAxll; >О Ух'!:- О, х е JRm,
что означает положительную определенность матрицы АТА. •
Лемм а 5.4. Вектор х е JRm является решением однородной сис­
темы
АТАх = 0
тогда и только тогда, когда Ах= О.
(5.94)
Доказательство. Если х является решением системы (5.94), то из
равенства (5.93) следует, что 11Axll2 =О, то есть Ах= О.
Если же Ах = О, то умножив обе части этого равенства слева на Ат,
придем к (5.94). •
Лемма 5.5. Матрица АТА вырождена тогда и только тогда, когда
столбцы матрицы А линейно зависимы.
190

192. § 5.12. Линейная задача метода наименьших квадратов
Доказательство. Напомним, что квадратная матрица АТА вырож­
дена тогда и только тогда, когда однородная система (5.94) имеет нетри­
виальное решение х "1= О.
Пусть матрица АТА вырождена их - нетривиальное решение сис­
темы (5.94). Тогда Ах= О в силу леммы 5.4, и в силу леммы 5.2 столбцы
матрицы А линейно зависимы.
Пусть теперь столбцы матрицы А линейно зависимы. Тогда в силу
леммы 5.2 существует вектор х -1= О такой, что Ах= О и поэтому х явля­
ется решением системы (5.94). Следовательно, матрица АТА вырож­
дена.•
Теорем а 5.6. Нормальная система метода наименьших квадратов
(5.94) имеет решение Это решение единственно тогда и только
тогда, когда столбцы матрицы А линейно независимы.
Доказательство. Пусть х е JR.m - произвольное решение одно­
родной системы (5.94). Тогда в силу леммы 5.4 Ах = О и поэтому
(Ать, х) = (Ь, Ах) = (Ь, О) = о.
Таким образом, правая часть нормальной системы (5.92) ортого­
нальна всем решениям однородной системы (5.94). Следовательно, в
силу теоремы Фредгольма система (5.92) имеет решение.
Напомним, что решение системы линейных алгебраических уравне­
ний с квадратной матрицей единственно тогда и только тогда, когда
матрица системы невырождена. Из леммы 5.5 следует, что решение
нормальной системы единственно тогда и только тогда, когда столбцы
матрицы А линейно независимы. •
В силу теоремы 5.5 решения линейной задачи метода наименьших
квадратов и нормальной системы (5.94) совпадают. Поэтому теорему
5.6 можно переформулировать следующим образом.
Теорема 5.7. Линейная задача метода наи-иеньших квадратов
имеет решение Это решение единственно тогда и только тогда,
когда столбцы матрицы А линейно независимы. •
Как следует из леммы 5.3, в случае, когда столбцы матрицы А
линейно независимы, матрица АтА - симметричная и положительно
определенная. Поэтому решение нормальной системы (5.94) можно
найти методом Холецкого примерно за т3 / 3 арифметических операций.
Правда, для формирования системы (с учетом симметричности мат­
рицы АТА) нужно примерно п2т арифметических операций. Если п » т,
191

193. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
то основные затраты машинного времени будут произведены на этапе
формирования матрицы лrл.
3 а меч ан и е. Если т <К п, то матрица АТА и вектор лть содер­
жат т2 <К п и т <К п элементов. Поэтому процесс их формирования
можно рассматривать как сжатие данных.
2. Алrоритм Грама-Шмидта и QR-разложение матрицы А.
С представлением квадратной матрицы А в виде произведения ортого­
нальной матрицы Q на верхнюю треугольную матрицу R, то есть в виде
A=QR (5.95)
мы уже встречались в § 5.1 О.
В случае, когда А - прямоугольная матрица размера пхт, будем
называть QR-разложением матрицы А ее представление в виде (5.95),
где Q - прямоугольная матрица размера пхт с ортонормированными
столбцами q1, q2, ... , Чт• а R - верхняя треугольная квадратная матрица
размера тхт с элементами rij.
3 а меч ан и е. Ортонормированность столбцов матрицы Q озна­
чает, что (q;. qj) =О для всех i '# j и (qj, q) = 1 для всехj, что экви­
валентно выполнению равенства
QTQ= Е,
где Е - единичная матрица порядка т.
(5.96)
Заметим, что равенство (5.95) означает, что существуют векторы q1,
q2, .. " Чт е Rm и коэффициенты rik• 1 s i s k s т такие, что для всех
k = 1, 2, .. " т столбцы ak матрицы А могут быть представлены в виде
линейной комбинации
k
ak= L'ikЧi·
i=I
Применим классический алгоритм Грама 1-Шмидта2 для ортого­
нализации столбцов а 1 , а2, •• " ат матрицы А, предполагая, что они
линейно независимы. Напомним, что этот алгоритм состоит из т шагов,
192
1 Иорген Педерсен Грам (1850--1916) - датский математик.
2 Эрхард Шмидт (1876-1959) - немецкий математик.

194. § 5.12. Линейная задача метода наименьших квадратов
на каждом из которых вычисляются очередной вектор qk и коэффици­
енты rik' 1$ i $ k.
На первом шаге полагают r11 = lla1ll2 и q1 = a1/r11 •
Пусть на (k-1 )-м шаге найдена ортонормированная система векторов
q1, q2, ... , Чk-J· Тогда на k-м шаге производят следующие вычисления:
k-1
'iik = ak - L r;k Ч;'
i=I
(5.97)
(5.98)
(5.99)
Заметим, что qk '*О и rkk = 11 ikll2 '*О, так как в противном случае
k-l
ak = Lr;kЧ; ·
1=!
(5.100)
Так как каждый из векторов Ч;. 1 $ i < k является линейной комбина­
цией векторов а 1 , а2, ... , ak- 1, то равенство (5.100) означает, что век­
тор ak является линейной комбинацией векторов а 1 , а2, ... , ak _ 1, что
противоречит предположению о том, что столбцы матрицы А линейно
независимы.
Обратим внимание на то, что llчkll 2 = 1 и (qk, q) =О для всехj = 1, 2,
..., k - 1. Действительно, в силу формул (5.98), (5.99) имеем
k- l
rkk(Чk• Ч) = ( qk, Чj) = (ak, Чj)- Lr;k(q;, Чj) = rjk -r;k =О·
i=I
Таким образом, полученная на k-м шаге алгоритма система векторов q1,
q2, ... , qk также является ортонормированной.
Теорем а 5.8. Пусть А - матрица размера пхт, столбцы которой
линейно независимы Тогда существуют единственная матрица Qраз­
мера пхт с ортонормированными столбцами и верхняя треугольная
матрица R с положительными диагональными элементами r;; (1 $ i $ т)
такие, что справедливо представление (5.95).
193

195. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
До к аз ат ель ст в о. Воспользуемся алгоритмом Грама-Шмидта
(5.97Н5.99) и получим матрицу Q с ортонормированными столбцами
q1, q2, ... , Чти верхнюю треугольную матрицу R с элементами rik• 1$ i $
$ k $ т (при k < i полагаем r;k = О).
Запишем формулу (5.98) в виде
k-1 k
ak = 'iik + L r;kЧ1 = LrikЧ, ·
i=I i=
Последнее равенство и означает, что алгоритм Грама-Шмидта дает
QR-разложение матрицы А.
Докажем теперь единственность матриц Q и R. Используя разложе­
ние (5.95) и равенство (5.96), имеем
АТА = [QR]TQR = RTQTQR = RTR.
Заметим, что матрица L = Rт - нижняя треугольная. Поэтому для мат­
рицы АТА мы получили разложение Холецкого (см. § 5.8):
(5.101)
Как следует из результатов § 5.8, матрица L в этом разложении опреде­
ляется едиственным образом. Поэтому матрицы R = Lт и Q = A.R-1
также определяются однозначно. •
З. Модифицированный алгоритм Грама-Шмидта. К сожалению,
классический алгоритм Грама-Шмидта обладает чрезмерно высокой
чувствительностью к вычислительной погрешности. Поэтому для чис­
ленной ортогонализации столбцов матрицы А используется модифици­
рованный алгоритм Грама-Шмидта, устойчивый к вычислительной
погрешности.
При отсутствии вычислительной погрешности этот алгоритм дает те
же матрицы Q и R, что и алгоритм (5.97)---(5.99).
На k-м шаге этого алгоритма получают очередной столбец qk мат-
рицы Q, модифицированные столбцы aik1 1
коэффициенты rkj для}= k, k + ," , т.
На первом шаге полагают
r11=lla1ll2· ч1=a1lr11•
a~I) = Q· • 2J J' 1= ,".,т.
194
(k)
ат матрицы А и

196. § 5.12. Линейная задача метода наименьших квадратов
Пусть на (k - 1)-м шаге получены столбцы q1, q2, ..., qk _ 1 и модифи-
(k- 1) (k-1) (k-1)
цированные столбцы ak , ak+ 1 , ".,ат . Тогда на k-м шаге про-
изводятся следующие вычисления:
rн = llaik-IJll2• Чk = a~k-I)lrн,
(k)
rk1= (а1 , qk), J = k + 1, "., т,
(k) (k-1)
а1 = а1 - rk;Чk, j = k + 1, "., т.
Замечание. Для получения QR-разложения матрицы А могут
быть применены и другие методы. Часто используется метод отра­
жений, основанный на преобразованиях Хаусхолдера (см.§ 5.10) и
обладающий лучшими, чем модифицированный алгоритм Грама­
Шмидта свойствами вычислительной устойчивости.
4. Использование QR-разложения для решения линейной задачи
метода наименьших квадратов. Пусть QR-разложение матрицы А
найдено. Тогда согласно теореме 5.5 вектор х, являющийся решением
линейной задачи метода наименьших квадратов, удовлетворяет нор­
мальной системе (5.92). Используя разложения (5.95) и (5.101), запи­
шем нормальную систему в виде
Положив с = Qть и умножив левую и правую части этой системы на
(RT)-1, приходим к системе линейных алгебраических уравнений с
верхней треугольной матрицей
Rx =с, (5.102)
решение которой совпадает с решением линейной задачи метода
наименьших квадратов.
Таким образом, для решения линейной задачи метода наименьших
квадратов можно сначала модифицированным методом Грама-Шмидта
найти QR-разложение матрицы А, затем вычислить вектор с = QТЬ и,
наконец, найти х как решение системы (5.102).
Однако, если формально действовать по этой схеме, то на этапе
вычисления вектора с умножением матрицы QT на вектор Ь можно поте­
рять все преимушества в вычислительной устойчивости, которые были
получены переходом от классического алгоритма Грама-Шмидта к его
модифицированному варианту.
195

197. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Для сохранения хороших свойств вычислительной устойчивости
вектор с= (с 1 , с2, •. "ст)т вычисляют иначе. Сначала полагают r (О)= Ь,
а затем для k = 1, 2, "" т проводят следующие вычисления
(k-1) (А) (k-1)
ck=(r ,qk), r =r -ckqk.
В результате получают вектор с и невязку r = r (т) = Ь - Ах .
Обратим внимание на то, что основные вычислительные затраты при
решении линейной задачи метода наименьших квадратов производятся
на этапе получения QR-разложения. В итоге время, необходимое для
решения задачи с помощью QR-разложения примерно вдвое превышает
время, необходимое для решения с использованием нормальной сис­
темы.
5. Сингулярное разложение матрицы. Пусть А - вещественная
матрица размера пхт, где п ~ т. Тогда существуют такие ортогональ­
ные матрицы U и V размера пхп и тхт соответственно, что
А= ur.vr. (5.103)
Здесь
а I о о о
о а2 о о
о о аз о
t=
............... "
о о о ат
о о о о
о о о ". о
диагональная матрица размера пхт с элементами а 1 ~ а2 ~ а3 ••• ~ат~ О
на главной диагонали.
Разложение (5.103) называется сингулярным разложением матрицы
А или SVD-разложением 1• Числа а1 , "" ат называются сингулярными
числа111и матрицы А. Эти числа определяются по матрице А однозначно
и являются важными ее характеристиками. Например, число ненуле­
вых сингулярных чисел совпадает с рангом матрицы.
1 От английского singular value decomposition.
196

198. § 5.12. Линейная задача метода наименьших квадратов
Сингулярное разложение существует более 100 лет. Оно было неза­
висимо открыто в 1873 г. Бельтрами 1 и в 1874 г. Жорданом 2 для квад­
ратных матриц. В 30-е годы ХХ в. оно было распространено на прямо­
угольные матрицы. В вычислительную практику SVD вошло в 60-е
годы и стало важнейшим инструментом вычислений.
6. Использование сингулярного разложения для решения
линейной задачи метода наименьших квадратов. Пусть разложение
(5.103) получено. Пусть ранг матрицы А равен r, т.е. пусть cr1 ~ ". cr, >О
и cr, + 1 = ... = crm = О. Нашей целью является минимизация величины
iirll2 = llb-Axll2.
Так как матрица U ортогональна, то норма невязки r не изменится
после ее умножения слева на сfГ. Таким образом,
llAx-bll; = llUr(Ax-b)ll; = iiuтm:vrx- uть11; = ll1:VТx- uтьll~.
Обозначая у = vтх и d = UТЬ, мы приходим к эквивалентной задаче
минимизации величины
... + (а,у, - d,)2 + d?+ 1 + ". + d~.
2 2
Ясно, что минимум равен d,+ 1 + ... + dm и достигается он при у 1 =
= d1/cr1, ".,у,= d,la,. После того как оказался найденным вектор у,
осталось положить х = Vy. Если r = т, то решение найдено одно­
значно. Если же r < т, то компоненты у,+ 1, ••• , Ут могут быть выбраны
произвольным образом и, следовательно, задача имеет бесконечно
много решений. Выбор у,+ 1 = ". = Ут =О дает решение х с минималь­
ной нормой (это решение называется псевдорешением системы (5.91).
Понятно, что наличие малых сингулярных чисел а, приводит к тому,
что малые погрешности в задании величин d, приводят к большим
погрешностям в вычислении компонент у1 = d, /а,. В этом случае задача
является плохо обусловленной. Правильное использование SVD пред­
полагает наличие некоторого допуска а• > О. Все сингулярные числа
1 Эудженио Бельтрами (1835-1900) - итальянский математик.
3 Камиль Мари Эдмон Жордан (1838-1922) - французский "dаТе"dатик, внесший зна­
чительный вклад в алгебру, теорию чисел, теорию функций, геометрию, топологию и
днфференцнальные уравнения.
197

199. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
cr, S cr. считаются пренебрежимо малыми и заменяются нулями, а соот­
ветствующее значения у, полагаются равными нулю.
Заметим, что увеличение значения параметра cr. приводит к увели­
чению нормы невязки; однако при этом уменьшается норма решения
и оно становится менее чувствительным к входным данным.
7. Дополнительная информация о сингулярном разложении. Обо­
значим столбцы матрицы U через и 1 , "., "п• а столбцы матрицы V -
через v1 "" vm. Векторы и, и v, называются соответственно левыми
и правыми сингулярными векторами матрицы А.
Равенство (5.90) можно записать в виде AV = ur. или Ати = VI:Т.
Сравнивая эти матричные равенства по столбцам, видим, что сингуляр­
ные векторы обладают следующими свойствами:
А v, = cr, и,, Ати, = cr, v,, 1 :5 i :5 т.
Из этих равенств следует, в частности, что
т - 2
А Av, - cr,v,, 1 :5 i :5 т.
Таким образом, квадраты сингулярных чисел матрицы А совпадают
с собственными значениями матрицы АтА. Для симметричных матриц
сингулярные числа просто равны модулям собственных значений.
Обратим теперь внимание на норму матрицы А. Делая замену у= Vx
и учитывая, что умножение вектора на ортогональную матрицу не
меняет его евклидовую норму, имеем:
llAll2 = max 11Axll2 = max llUTAxll 2 = max llr.VТxll 2 =
llxli2 = 1 llxll2 = 1 llxll2 = 1
= max llr.yll2 = max JcriYi + ". + cr~y~ = cr1 •
1И 2 = 1 11у11 2 = 1
Отметим также, что отношение cr1lcrm часто используется в качестве
числа обусловленности матрицы А. Для квадратной невырожденной
матрицы А действительно cond2(A) = crifcrm.
Более подробно о сингулярном разложении и его разнообразных
приложениях см. в [31, 54).
8. Сравнение различных методов решения линейной задачи
метода наименьших квадратов. Мы рассмотрели следующие методы
решения линейной задачи метода наименьших квадратов:
1) использование нормальной системы метода наименьших квадратов;
198

200. § 5.13. Дополнительные замечания
2) использование QR-раэложения~
3) использование сингулярного разложения матрицы А.
Какой метод следует предпочесть при решении линейной задачи
метода наименьших квадратов? Наиболее быстрым является метод нор­
мальных уравнений. Затем идет метод, основанный на использовании
QR-разложения. Наконец, наибольших вычислительных затрат требует
использование сингулярного разложения.
Если матрица А хорошо обусловлена, то следует предпочесть метод
нормальных уравнений. Однако, если матрица А плохо обусловлена,
нормальная система имеет число обусловленности, примерно равное
квадрату числа обусловленности матрицы А. Поэтому можно ожидать,
что при использовании этого метода будет потеряно вдвое больше зна­
чащих цифр по сравнению с методами, основанными на QR-раэложении
или сингулярном разложении матрицы.
В случае, когда матрица А плохо обусловлена, но система её столб­
цов линейно независима и не близка к линейно зависимой, наиболее
подходящим методом является, по-видимому, использование QR-разло­
жения.
Наиболее медленным, но наиболее надежным методом является
использование сингулярного разложения. Особенно важно использова­
ние сингулярного разложения в случае, когда система столбцов мат­
рицы А линейно зависима или близка к линейно зависимой.
Таким образом, выбор метода решения зависит от того, что важнее
для пользователя: скорость решения задачи или надежность получен­
ных результатов.
§ 5. 13. Допоnнитеnьные замечания
1. Более подробное и в то же время доступное изложение рассмот­
ренных в этой главе вопросов можно найти, например, в [46, 47, 81,
107, 5*, 16*, 20•]. Особое внимание следует обратить на книгу [31],
представляющую собой удачное сочетание учебного пособия и спра­
вочника по методам матричных вычислений.
2. Для решения систем линейных алгебраических уравнений
создано высококачественное и бесплатно распространяемое програм­
мное обеспечение. Пакеты BLAS, LINPACK, EISPACK и LAPACK,
ориентированные на системы уравнений с заполненными матрицами,
доступны по адресу http://www.пet1b.org. Пакет SPARSКIT, предназ­
наченный для решения систем уравнений с разреженными матри­
цами, доступен по адресу http://www.cs.umn.edu/Research/arpa/SPARSKIТ/.
199

201. Глава 5. Прямые методы решения систем линейных алгебраических уравнений
Обратим также внимание на пакет LinPar, доступный по адресу
http://www.ict.nsc.ru/linpar/.
3. Интересной модификацией метода Гаусса является алгоритм
Краута, основанный на изменении порядка выполнения арифметиче­
ских операций. Существуют два случая, когда эта модификация может
иметь преимущества. Во-первых, алгоритм Краута выгоден тогда, когда
для вычислений используется калькулятор, так как алгоритм позволяет
избегать выписывания промежуточных результатов. Во-вторых, он при­
вqр:ит к наименьшей вычислительной погрешности при условии, что
вычисления ведутся на компьютере, обладающем сравнительно быст­
рой арифметикой с расширенной точностью или особенно быстрой
т
операцией вычисления скалярных произведений (х, у) = Lх, у,. Обсу-
1=1
ждение модификации Краута можно найти, например, в [81, 107].
4. Иногда вместо метода Гаусса используют метод Гаусса-Жордана,
отличающийся от метода Гаусса тем, что на k-м шаге прямого метода
обнуляются не только элементы k-го столбца матрицы, находящиеся под
главной диагональю, но и элементы k-го столбца, находящиеся над
главной диагональю. В результате матрица системы приводится не к
нижнему треугольному виду, а к диагональному виду.
Отметим, что прямой ход метода Гаусса-Жордана требует при­
мерно т3/2 арифметических операций и по затратам машинного вре­
мени проигрывает методу Гаусса примерно в полтора раза.
5. Следует отметить, что в данной главе оказались практически не
отраженными прямые методы решения систем уравнений с разрежен­
ными матрицами (исключение составляет § 5.9, посвященный методу
прогонки). Желающим найти доступное изложение современных пря­
мых методов, предназначенных для решения очень больших линейных
систем с разреженными матрицами, можно посоветовать обратиться
к [48]. Укажем также на книги [38, 77, 116], специально посвященные
технологии разреженных матриц.
6. Предположим, что после того, как было найдено решение х сис-
темы Ах = Ь, возникла необходимость решить систему Ах = Ь с матри­
цей А , отличающейся от матрицы А несколькими элементами. Напри­
мер, могло выясниться, что заданные ранее элементы содержали
грубые ошибки. Возможно также, что решаемая задача такова, что в
ней элементы матрицы последовательно меняются, а правая часть оста­
ется неизменной.
200

202. § 5.13. Дополнительные замечания
Разумеется, х можно найти, решив систему снова и проигнорировав
полученную на предыдущем этапе информацию. Однако в рассматри­
ваемом случае можно найти поправку Лх = х -х к найденному ранее
решению, использовав всего О(т2) операции.
Пусть А = А - иvТ, где и и v - векторы размерности т. Справед­
лива фор.мула Шерманна-Моррисона
А- 1 = А-1 + a(A-lu)(vтA- 1 ),
где а= 1/(1 - vTA-1u). Применяя ее, приходим к следующему алгоритму:
1°. Систему Ау = и решают относительно у.
2°. Систему ATz = v решают относительно z.
3°. Вычисляют а= 1/(1 - vту), р = zTb и Лх =ару.
4°. Полагают х = х + Лх.
Суммарное число операций будет действительно составлять О{т2),
если для решения систем Ау = и и АТz = v применить обратную под­
становку с использованием LU-разложения матрицы А, найденного
ранее на этапе решения системы Ах = Ь.
В случае, когда матрица А отличается от матрицы А только одним
элементом а,1 = а,1 + Ла,1 , можно положить и= Ла1Jе1 , v = е1, а указан­
ный алгоритм упростить следующим образом:
1°. Систему Ау = ЛalJ е, решают относительно у.
2°. Систему Атz = е1 решают относительно z.
3°. Вычисляют а= 1/(1 - у), Р = zть и Лх =ару.
4°. Полагают х = х + Лх.
Основываясь на формуле Шерманна-Моррисона, можно указать
и способ пересчета LU-разложения матрицы.
О формуле Шерманна-Моррисона и ее применениях см. [54, 31].
201

203. Гла во 6
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Системы линейных алгебраических уравнений можно решать как с
помощью прямых, так и итерационных методов. Для систем уравнений
средней размерности чаще используют прямые методы.
Итерационные методы применяют главным образом для решения
задач большой размерности, когда использование прямых методов невоз­
можно из-за ограничений в доступной оперативной памяти компьютера
или из-за необходимости выполнения чрезмерно большого числа ариф­
метических операций. Большие системы уравнений, возникающие
в приложениях, как правило, являются разреженными. Методы исклю­
чения для решения систем с разреженными матрицами неудобны,
например тем, что при их использовании большое число нулевых эле­
ментов превращается в ненулевые и матрица теряет свойство разрежен­
ности. В противоположность им при использовании итерационных
методов в ходе итерационного процесса матрица не меняется, и она,
естественно, остается разреженной. Ббльшая эффективность итераци­
онных методов по сравнению с прямыми методами тесно связана с воз­
можностью существенного использования разреженности матриц.
Применение итерационных методов для эффективного решения
большой системы уравнений требует серьезного использования ее
структуры, специальных знаний и определенного опыта. Именно
поэтому разработано большое число различных итерационных
методов, каждый из которых ориентирован на решение сравнительно
узкого класса задач, и существует довольно мало стандартных про­
грамм, реализующих эти методы.
В этой главе будут рассмотрены наиболее простые и известные
итерационные методы, позволяющие решать достаточно широкий
класс систем.
§ 6.1. Метод простой итерации
1. Приведение системы к виду, удобному для итераций. Для того
чтобы применить метод простой итерации к решению системы
линейных алгебраических уравнений
Ах=Ь (6. 1)
202

204. § 6.1. Метод простой итерации
с квадратной невырожденной матрицей А, необходимо предварительно
преобразовать эту систему к виду
х= Вх+с. (6.2)
Здесь В - квадратная матрица с элементами Ь,1 (i, j = 1, 2, .. " т); с -
вектор-столбец с элементами с, (i = 1, 2, .. " т).
В развернутой форме записи система (6.2) имеет следующий вид:
Х1 = Ь11Х1 + Ь12Х2 + Ь13Х3 + ". + Ь1тХт + CI,
Х2 = Ь21Х1 + Ь22Х2 + Ь23Х3 + ". + Ь2тХт + с2,
(6.3)
Как правило, операция приведения системы к виду, удобному для
итераций (т.е. к виду (6.2)), не является простой и требует специ­
альных знаний, а также существенного использования специфики
системы. В некоторых случаях в таком преобразовании нет необходи­
мости, так как сама исходная система уже имеет вид (6.2). 1
Самый простой способ приведения системы к виду, удобному для
итераций, состоит в следующем. Из первого уравнения системы (6.l)
выразим неизвестное х 1 :
-1
Х1 = а11 (Ь1 - a1r2 - а13Х3 - ." - al тхт),
из второго уравнения - неизвестное х2 :
-1
Х2 = а22 (Ь2 - 021Х1 - а23Х3 - ". - 02тхт),
и т.д. В результате получим систему
Х1 = Ъ12Х2 + Ь13Х3 + ". + ьl,m-lxm-1 + Ь1тХт + С1,
Х2 = bz1X1 + bz3X3 + + b2,m- lxm- I + bzmXm + Cz,
Х3 = Ь31Х1 + Ь32Х2 + + Ъз,т-lхт-1 + Ь3тХт + С3,
(6.4)
хт = Ьт1Х1 + Ьт2Х2 + Ьт3Х3 + ". + ьт,т- lхт-1 + ст,
в которой на главной диагонали матрицы В находятся нулевые эле­
менты. Остальные элементы вычисляются по формулам
ь,} =-a,J/all, с,= b,lall (i,J = , 2, "" т,j *' i). (6.5)
1 Такие системы возникают, например, при аппроксимации интегральных уравнений
Фредгольма второго рода (см. гл. 16).
203

205. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Конечно, для возможности выполнения указанного преобразования
необходимо, чтобы диагональные элементы матрицы А были нену­
левыми.
Часто систему (6. J) преобразуют к виду х = х - т (Ах - Ь), где т -
специально выбираемый числовой параметр (см. § 6.4).
2. Описание метода простой итерации. Выберем начальное прибли­
жение х<0> = (х0>, х~0>, .. .,х~> ). Подставляя его в правую часть системы
(6.2) и вычисляя полученное выражение, находим первое приближение
хО) = Вх<0> + с.
Подставляя приближение х< 1 > в правую часть системы (6.2), получаем
х<2> =ВхО> + с.
Продолжая этот процесс далее, получаем последовательность
х<0>, хО), ..., х(п), . " приближений, вычисляемых по формуле
x(k+l)=Bx(k)+c, k=O, 1,2, .... (6.6)
В развернутой форме записи формула (6.6) выглядит так:
Когда для итераций используется система (6.4) с коэффициентами,
вычисленными по формулам (6.5), метод простой итерации принято
называть методом Якоби 1.
3. Сходимость метода простой итерации
Теорема 6.1. Пусть выполнено условие
llBll < 1. (6.8)
Тогда:
1) решение х, системы (6.2) существует и единственно;
1 Карл Густав Якоб Якоби (1804-1851) - немецкий математик.
204

206. § 6.1. Метод простой итерации
2) при произвольном начальном приближении x(OJ метод простой
итерации сходится и справедлива оценка погрешности
llx(nJ_xll $ 11Bllnllx(0J-xll. (6.9)
Доказательство. 1) Из курса линейной алгебры известно, что
система линейных алгебраических уравнений имеет единственное
решение при любой правой части тогда и только тогда, когда соответст­
вующая однородная система имеет только нулевое решение. Пусть х -
решение однородной системы х = Вх. Тогда llxll = llBxll $ llBll · llxll . Так
как по условию llBll < l, это неравенство возможно только при llxll = О.
Следовательно, х = О и тем самым первое утверждение теоремы
доказано.
2) Вычитая из равенства (6.6) равенство х = Вх +с, получаем
x(k+ 1 >-х =B(x<kJ _х). (6.10)
Вычисляя норму левой и правой частей этого равенства и используя
неравенство llB(x<*>-x)ll $ llBll llx<k)_xll, имеем llx(k+ 1>-xil $
$ llBll lix<k) - х 11 . Так как это неравенство верно для всех k ~ О, то
llx<п>-xll $ llB!lllx<п- 1 >-xll $ llBll2 11x<n-2>-xi1 $ ...
... $ llBlln- t llxO)- xll $ llBllnllx<0>- xll.
Справедливость неравенства (6.9) установлена. Учитывая, что
llx<OJ _xll не зависит от п, а llBlln --+ О при п --+ оо, получаем из него,
что llx<п>-xll --+О при п--+ оо. 8
Замечание 1. Теорема 6.1 дает простое достаточное условие
(6.8) сходимости метода простой итерации. Грубо это условие
можно интерпретировать как условие достаточной малости эле­
ментов bij матрицы В в системе, приведенной к виду (6.2).
Замечание 2. Если llBll = llBll00 , то условие (6.8) принимает
вид
т
llBll 00 = m~x L bu < 1.
1S1Sm j=I
Для метода Якоби это условие в силу равенств Ь;; = О, b;j =
= - aijla;; для i * j эквивалентно условию строчного диагональ­
ного преобладания (5.45).
Таким образом, для сходимости метода Якоби достаточно,
чтобы матрица А была близка к диагональной.
205

207. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Отметим еще одно условие столбцового диагонального преобла­
дания
т
L /а,1 / < /aJI/, j = 1, 2, "., т. (6.11)
1= 1
'"'1
Правда, оно не является достаточным для сходимости метода Якоби.
Замечание 3. Из оценки (6.9) следует, что при выполнении
условия (6.8) метод простой итерации сходится со скоростью гео­
метрической прогрессии, знаменатель которой q = llBll. Скорость
сходимости тем выше, чем меньше величина llBll . Хотя метод схо­
дится при любом начальном приближении х(О), из оценки (6.9)
можно сделать полезный вывод: начальное приближение жела­
тельно выбирать близким к решению.
Замечание 4. Оценка погрешности (6.9) является априорной.
Ее использование для формулировки критерия окончания итера-
ций затруднительно, так как значение llx<0J- х 11 неизвестно, а
его грубое оценивание заведомо приведет к завышению необхо­
димого числа итераций.
4. Апостериорная оценка погрешности
Предложение 6.1. Если выполнено условие (6.8), то справедлива
апостериорная оценка погрешности
(6.12)
Доказательство. Запишем равенство (6.10) при k = п - 1 в виде
х(п) _х = В(х<п- 1 >-х<п)) + В(х<п) _ х).
Тогда
lix<пJ - xll = llB(x<п- IJ -х<пJ) + В(х<п> - x)ll ~
::5: llBll llx<n-IJ_x(nJll + llBll llx<n)_ xll.
Для завершения доказательства осталось заметить, что полученное
неравенство эквивалентно неравенству (6.12). 8
206
Замечание. Величину, стоящую в правой части неравенства
(6.12), можно легко вычислить после нахождения очередного при­
ближения х<п>. Если требуется найти решение с точностью Е, то
в силу (6.12) следует вести итерации до выполнения неравенства
__l!!L llx(n)_x(n-IJll<E. (6.13)
1-llвll

208. § 6.1. Метод простой итерации
Таким образом, в качестве критерия окончания итерационного про­
цесса может быть использовано неравенство
lx(n)_x(n-1)11 <Е 1 , (6.14)
1-llвll
где Е 1 = /iВiГ Е.
В практике вычислений иногда используют привлекательный своей
простотой критерий окончания
llx(n)_x(n-l)I <Е. (6.15)
Отметим, что для метода простой итерации его применение обос­
новано только тогда, когда llBll ~ 1/2 (в этом случае (l - llBll )/ llBll ~ l
и выполнение неравенства (6.15) влечет за собой выполнение нера­
венства (6.14)). Однако в большинстве реальных случаев величина llBll
оказывается близкой к единице и поэтому (l - 11В11 )/ 11В11 « l . В этих
случаях Е 1 « Е и использование критерия (6.15) приводит к существенно
преждевременному окончанию итераций. Величина llx(n) -х<п- 1>11 здесь
оказывается малой не потому, что приближения х<п - I) и х<п> близки к
решению, а потому, что метод сходится медленно (ер. с замечанием
на с. 104).
Пр им ер 6.1. Использовав метод простой итерации в форме Якоби,
найдем решение системы
х2 + О.5х3 = 7.5.
5х2 + 2. l2x3 = -8.68,
О.5х 1 + 2. l2x2 + 3.6х3 = -0.24,
с точностью Е = lо-3 в норме 11 •11 00 •
(6.16)
Вычислив коэффициенты по формулам (6.5), приведем систему к
виду (6.4)
х 1 = O.l6x2 - О.08х3 + 1.2,
х2 = О.2х 1 - О.424х3 - l.736, (6.17)
х3 = -О. 389х 1 - О.5889х2 - 0.0667.
В последнем уравнении коэффициенты даны с точностью до погреш­
ности округления. Здесь
[
о
В= 0.2
-0.1389
0.16 -0.08]
о -0.424 ,
-0.5889 о
[
1.2 Jс= -1.736 .
-0.0667
(6.18)
207

209. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Достаточное условие сходимости метода простой итерации
выполнено, так как llBll00 = max{0.24, 0.624, 0.7278} = 0.7278 < 1.
Примем за начальное приближение к решению векторх<0J =(О, О, О)Т
и будем вести итерации по формуле (6.6) до выполнения критерия
окончания (6.14), где в данном случае i: 1 = (1 - 0.7278)/0.7278· I0-3 ::::
:::: 0.37 · 10-3. Значения приближения в табл. 6.1 приводятся с четырьмя
цифрами после десятичной точки.
Таблица 6.1
п о 1 2 3 4
(п)
Х 0.0000 1.2000 0.9276 0.9020 0.8449
(п)
Х2 0.0000 -1.7360 -1.4677 -1.8850 -1.8392
(п)
Х3 0.0000 4>.0667 0.7890 0.6688 0.9181
l/x(n) _x(n- l)lloo - 1.7360 0.8557 0.4173 0.2493
Продолжение табл. 6)
п
." 12 13 14 15
(п
0.8006 0.8003 0.8002 0.8001х ...
(п)
-1.9985 -1.9993 -1.9995 -1.9998Х2 ...
(•)
0.9987 0.9990 0.9995 0.9997Х3 ...
llx<•>-x<n- 1>1100 ... 0.0018 0.0008 0.0005 0.0003
При п = 15 условие (6.14) выполняется и можно положить х 1 =
=-0.800 ± 0.001, х2 = -2.000 ± 0.001, х3 = 1.000 ± 0.001. В данном
случае точные значения решения х1 =-0.8, х2 =-2, х3 = 1 нам известны
(см. пример 5.16).
Заметим, что в действительности решение с точностью до Е = 1о-3
было получено уже при п = 13. А
S. Необходимое и достаточное условие сходимости. Поскольку
условие (6.8) является лишь грубым достаточным условием сходи­
мости метода простой итерации, представляет интерес формулировка
необходимого и достаточного условия сходимости.
208

210. § 6.1. Метод простой итерации
Пусть Л. 1 , Л.2, •••, Л.т - собственные значения матрицы В. Спек­
тральным радиусом матрицы В называется величина р(В) = max 1Л,1 .
1 S1Sm
Теорема 6.2. Метод простой итерации (6.6) сходится при любом
начальном приближении х(О) тогда и только тогда, когда р(В) < 1, т.е.
когда все собственные значения матрицы В по _wодулю меньше единицы.
•
Замечание. Для симметричной матрицы В ее спектральный
радиус р(В) совпадает с llBl2• Поэтому для сходимости метода
простой итерации с симметричной матрицей В условие llB12 < 1
является необходимым и достаточным.
6. Влияние ошибок округлении. Из-за наличия ошибок округ­
ления реально вычисляемые на компьютере приближения .Х<п> отли­
чаются от идеальных приближений х<п>. Поэтому нельзя утверждать,
что для любого Е >О найдется номер п 0 (Е), начиная с которого все при-
ближения будут находиться в Е-окрестности решения.
-
В действительности же существует некоторая Е -окрестность
решения, после попадания в которую приближения .Х<п> дальнейшего
уточнения при выполнении итераций не происходит. В подтверждение
сказанного приведем следуюший результат.
Теорема 6.3. Пусть llBll < 1. Предположим, что вычисляемая на
ко,wпьютере с помощью метода простых итераций последователь-
ность .Х<п> удовлетворяет равенствам
(6.19)
где ~(п) е Rm, jj~(n)jj <Б. Если вычисления по формулам (6.6) и (6.19)
начинаются С одного начального приближения х(О) = х(О) , то для всех
п ~ l справедливы следующие оценки погрешности:
llx<п) -х<п>I $ Е, (6.20)
11.Х<п> - х 11 s llBll п llx<0>- х 11 + Ё, (6.21)
llx<n> - х11 S J!!L 11.Х<п) -.Х<п - 1>11 + i ·
1- llвll '
здесь Е = __б_ •
1- llвll ·
(6.22)
209

211. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Таким образом, метод простых итераций устойчив, но гарантиро­
ванная точность метода ограничена снизу величиной &. Критерий
окончания (6.13) применим, если Ё « &.
§ 6.2. Метод Зейде111
1. Описание метода. Пусть система (6.1) приведена к виду (6.4)
с коэффициентами, вычисленными по формулам (6.5).
Метод Зейделя 1 можно рассматривать как модификацию метода
Якоби. Основная идея модификации состоит в том, что при вычислении
очередного (k + 1)-го приближения к неизвестному х, при i > 1
используют уже найденные (k + 1)-е приближения к неизвестным х1, .. "
х, _ 1, а не k-e приближения, как в методе Якоби.
На (k + 1)-й итерации компоненты приближениях(k+ I) вычисляются
по формулам
(k+ 1)
Х1 =
(k)
Ь12Х2 +
(k)
Ь13Х3 +
(k)
... + ьтхт + с,
(k+ )
Х2
ь (k +1)
2Х +
(k)
Ь23Х3
(k)
+ ... + Ь2тХт + С2,
(k+ 1)
Х3 =
ь (k +1)
ЗIХ
+ ь (k+ 1)
32Х2
(k)
+ ·" + ЬзтХт + С3,
(k+I) = Ь (k+I) + Ь (k+I) + Ь (k+I) +
Хт т1Х1 т2Х2 тзХз ···
Введем нижнюю и верхнюю треугольные матрицы
о о о о о Ь12 Ь1з
Ь21 о о о о о Ь23
В1= Ьз1 Ьз2 о ... о 1 В2= о о о
о о о ... о
Тогда расчетные формулы метода примут компактный вид:
х<* + I) = В 1 х<* + I) + B2x<k> +с.
1Людвиг Зейдель (1821-1896)- немецкий астроном и математик.
210
(6.23)
(6.24)

212. § 6.2. Метод Зейделя
Заметим, что В= В 1 + В2 и поэтому решение х исходной системы
удовлетворяет равенству
(6.25)
Метод Зейделя иногда называют также методом Гаусса-Зейделя,
процессом Либмана, методом последовательных замещений.
2. Достаточные условия сходимости.
Теорема 6.4. Пусть В< 1, где 1В - одна из норм В1 00, В1 1 •
Тогда при любом выборе начального приближения х<0> метод Зейделя
сходится со скоростью геометрической прогрессии. знаменатель
которой q ~ lBll. •
Доказательство этой теоремы опускаем. Оно довольно громоздкое,
хотя и не сложное. Приведем более компактное доказательство сле­
дующей теоремы, близкое к доказательству теоремы 6.1.
Теорем а 6.5. Пусть выполнено условие
(6.26)
Тогда при любом выборе начального приближения метод Зейделя схо­
дится и верна оценка погрешности
x<п>-xll ~ qnx<0>-xI,
где q = llB2ll/(l - lB111) < 1.
(6.27)
Доказательство. Вычитая из равенства (6.24) равенство (6.25),
имеем:
(6.28)
Вычисляя нормы левой и правой частей этого равенства и используя
свойства нормы, получаем:
lx(k+ 1J- х1 =llB 1 (х<*+ 1 > - х) + В2(х<*> - x)ll ~
~ llB111llx<k+ 1>-xll + llB211 llx<*>- xl/.
Следовательно,
x(k+ l) _ xll ~ qx(k) _xll,
где q= IB2ll/(I - llB11).
Так как это неравенство верно для всех k ~ О, то из него следует
оценка (6.27). В силу условия (6.26) имеем О ~ q < 1. Поэтому х<п) - х
при п - оо. •
211

213. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Особо выделим часто встречающийся на практике случай систем с
симметричными положительно определенными матрицами.
Теорема 6.6. Пусть А - симметричная положительно опреде­
ленная матрица. Тогда при любом выборе начального приближения х<0>
метод Зейделя сходится со скоростью геометрической прогрессии. •
Отметим, что никаких дополнительных априорных условий типа
малости нормы некоторой матрицы здесь не накладывается.
3. Апостериорная оценка погрешности
Предложение 6.2. Если выполнено условие llBll < 1, то для
метода Зейделя справедлива апостериорная оценка погрешности
llв2 ll
llx<nJ _.Xll ~ 1 - llвll llx<nJ _x(n- IJll, п ~ 1. (6.29)
Доказательство. Положим k = п - 1 и запишем равенство (6.28)
в следующем виде:
х<п>- х =В(х<пJ-х) + B2(x<n- 1 J-x<п>).
Тогда
llx<п>-xll ~ llBll llx<nJ _.Xll + llB211 llx<n- l) _x(nJll,
откуда и следует неравенство (6.29). •
Полученное неравенство позволяет сформулировать простой кри­
терий окончания итерационного процесса. Если требуется найти
решение с точностью Е > О, то итерации метода Зейделя следует вести
llв211
до выполнения неравенства l - llвll llx<n-l)_x(nJll < Е или эквива-
лентного ему неравенства
1 - llвll
где в2 = Тв;iГ в .
(6.30)
4. Геометрическая интерпретация метода. Приведем геометри­
ческую интерпретацию метода Зейделя при т = 2, т.е. когда он приме­
няется для решения системы
212
а 11х1 + a 1r-2 = Ь1 ,
az1X1 + a2r2 = h2.

214. § 6.2. Метод Зейделя
Рис. 6.1
Первое уравнение задает на плоскости х1 0-с2 прямую /1, второе -
прямую /2 (рис. 6.1 ). Расчетные формулы метода принимают вид:
(k + 1)
Х1 =
(k+l)_b (k+I)
Х2 - 21XI
где h12 = -a12la11• с1 = b1la11• Ь21 = -a21la22• с2 = b2la22·
Пусть приближение x(k) уже найдено. Тогда при определении x~k+ l)
координата х2 = x~k) фиксируется и точках перемещается параллельно
оси Ох 1 до пересечения с прямой /1. Координата х 1 точки пересечения
(k + 1) з -принимается за х 1 • атем точках перемещается вдоль прямои х 1 =
= x~k+ 1> до пересечения с прямой /2. Координата х2 точки пересечения
(k+ )
принимается за х2 •
На рис. 6.1, а, б приведены геометрические иллюстрации, отве­
чающие сходящемуся и расходящемуся итерационному процессу
Зейделя. Видно, что характер сходимости может измениться при пере­
становке уравнений.
Пр им ер 6.2. Использовав метод Зейделя, найдем решение системы
(6.16) С ТОЧНОСТЬЮ Е = J0-3.
После приведения системы к виду (6.17) убеждаемся, что 11Bll00
= 0.7278 < 1 и поэтому в силу теоремы 6.4 метод Зейделя сходится.
213

215. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Положим х<0> = (О, О, О)Т и будем вычислять последовательные при­
ближения по формулам
Здесь
x<k+ I) =
1
(k + 1) - о 2 (k + 1)
Xz - , Х1
(k) (k)
О.16х2 - О.08х3 + 1.2,
(k)
- О.424х3 - 1.736,
x~k + 1) = -O. l389x~k + 1) - 0.5889x~k + 1) - 0.0667.
[о 0.16 -o.o8j
В2 = О О -0.424
о о о
и llB21100 = 0.424. Будем вести итерации до выполнения критерия окон­
чания (6.30), где Е2 = 10-3 • (1 - 0.7278)/0.424 :::: 0.64 • 10-3. Значения
приближений с четырьмя цифрами после десятичной точки приведены
в табл. 6.2.
Таблица 6.2
п о 1 2 3 4
(11)
х, 0.0000 1.2000 0.9088 0.8367 0.8121
(п)
Х2 0.0000 -1.4960 -1.8288 -1.9435 -1.9813
(п)
Х3 0.0000 0.6476 0.8841 0.9616 0.9873
llx<•J -х<• - 1>11 оо - 1.4960 0.3328 0.1147 0.0378
Продолжение табл. 6.2
п 5 6 7 8
(п)
х, 0.8040 0.8013 0.8004 0.8001
(п)
Х2 -1.9938 -1.9980 -1.9993 -1.9998
(п)
Х3 0.9958 0.9986 0.9995 0.9998
llx<•> -х<• - 1>11 оо 0.0125 0.0041 0.0014 0.0005
При п = 8 критерий окончания выполняется и можно положить х 1 =
= 0.800 ± 0.001, х2 = -2.000 ± 0.001, х3 = 1.000 ± 0.001. Заметим, что
в действительности решение с точностью Е = 10-3 было получено уже
при п = 7. .6
214

216. § 6.3. Метод последовательной верхней релаксации
5. Необходимое и достаточное условие сходимости. Метод
Зейделя (6.24) может быть записан в эквивалентном виде
х<* + I) = Bx(k) + с,
где В = (Е - В1)- 1В2, с= (Е - В1 )- 1 с. В такой форме записи он пред­
ставляет собой метод простой итерации. Поэтому в силу теоремы 6.2
необходимым и достаточным условием сходимости метода является
выполнение неравенства р(В) < 1. Поскольку собственные числа
матрицы В совпадают с числами Л., являющимися решениями обоб­
щенной задачи на собственные значения В2х = Л.(Е - В 1 )х, спра­
ведлива следующая теорема.
Теорема 6.7. Метод Зейделя сходится при любом начальном при­
ближении х<0> тогда и только тогда, когда все решения обобщенной
задачи на собственные значения В2х = Л.(Е - В 1 )х по модулю меньше
единицы. 8
Замечание. Существует устойчивое заблуждение, связанное
с представлением о том, что метод Зейделя сходится быстрее, чем
метод Якоби. Это действительно так, если матрица А симметрична
и положительно определена (мы убедились в преимуществе
метода Зейделя для системы уравнении с такой матрицей, решив
примеры 6.1 и 6.2). Однако в общем случае возможны ситуации,
когда метод Якоби сходится, а метод Зейделя сходится медленнее
или вообще расходится. Возможны и противоположные ситуации.
Дело в том, что эти методы ориентированы на решение разных
классов систем: метод Якоби - на системы с матрицами, близ­
кими к диагональным, а метод Зейделя - на системы с матри­
цами, близкими к нижним треугольным.
§ 6.3. Метод последовательной верхней релаксации
Метод последовательной верхней релаксации является одним из наи­
более эффективных и широко используемых итерационных методов для
решения систем линейных алгебраических уравнений с симметричными
положительно определенными матрицами А. Этот метод часто называют
SОR-методом 1. Частично популярность SОR-метода можно объяснить
его простотой и тем, что он хорошо известен широкому кругу специа­
листов, занимающихся решением прикладных задач.
1 Or англ. successive over relaxation.
215

217. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Суть метода релаксации состоит в следующем. После вычисления
очередной 1-Й компоненты (k + 1)-го приближения по формуле метода
Зейделя
-(k + 1) - ь (k + 1) + ь (k + 1) + + ь (k + 1) + ь (k) +
Х; - ;1Х1 i2X2 ··· i,i-IXi-1 i,i+IXi+I ··•
... + b;mxj~ +С;
производят дополнительно смещение этой компоненты на величину
-(k+ 1) (k) .
(ro- )(х; -х; ), где ro - параметр релаксации. Таким образом, 1-я
компонента (k + 1)-го приближения вычисляется по формуле
xik+ 1) =X'jk + 1) + ((1) - 1)(x~k-+ 1) - x:k» = roxjk + 1) + (1 - (1) )xik).
На рис. 6.2 показано несколько первых итераций метода при зна­
чении параметра релаксации ro = 1.25.
Рис. 6.2
В обозначениях, используемых в § 6.2, компактная формула для
вычисления x<k + IJ записывается следующим образом:
x<k + I) = (1 - ro)x<kJ + roB 1x<k + I) + roB2x(k) + roc.
Как нетрудно видеть, при ro = 1 метод релаксации совпадает с
методом Зейделя. При ro > 1 его было принято называть методом после­
довательной верхней релаксации, а при ro < 1 - методом последова­
тельной нижней релаксации. В последнее время метод релаксации
216

218. § 6.3. Метод последовательной верхней релаксации
называют методом последовательной верхней релаксации для любых
значений ro.
Если А - симметричная положительно определенная матрица, то
при любом значении параметра ro (0 < ro < 2) метод релаксации схо­
дится. Часто оказывается возможным выбрать параметр ro > 1 так,
чтобы SОR-метод сходился существенно быстрее, чем методы Якоби и
Зейделя. Однако выбор параметра релаксации - довольно трудная
задача. Во многих случаях она решается экспериментальным путем.
Существуют различные модификации метода релаксации. Распро­
страненный вариант метода связан с использованием различных пара­
метров ro, для вычисления различных компонент х; очередного (k + 1)-го
приближения к решению.
Метод симметричной последовательной верхней релаксации (SSOR)
заключается в чередовании итераций по методу SOR с такими же итера­
циями, осуществляемыми для системы, в которой уравнения зануме­
рованы в обратном порядке.
Пр и мер 6.3. Использовав метод последовательной верхней релак­
сации с параметром ro = 1.12, найдем решение системы (6.16) с точ­
ностью Е = J0-3.
Приведем систему к виду (6.17), положим х<О) = (О, О, О)Т и будем
вычислять последовательные приближения по формулам:
xk+ 1>= (1-ro)xk> + ro(0.16x~k) _0.08x~k) + 1.2),
x~k+ J) = ro · 0.2xk+ IJ + (1-ro)x~k) + ro(-0.424x~k) _ l.736),
x~k + 1>= ro(- 0. l389xk + 1) - 0.5889x~k + 1»+ ( 1- ro)x~k) - ro · 0.0667.
Значения приближений с четырьмя цифрами после десятичной
точки приведены в табл. 6.3.
Таблица 6.3
п о 1 2 3 4 5
(п)
х, 00000 1 3440 о 8166 о 8094 о 7995 о 8001
(п)
Х2 о 0000 -1 6433 -1 9442 -1 9973 -1 9998 -2 0000
(п)
Х3 00000 о 8001 о 9846 о 9986 1 0001 1 0000
Сравнение с точным решением х 1 = 0.8, х2 = -2, х3 = 1 показывает,
что для получения приближения к решению с точностью Е = 1о-3 потре­
бовалось всего четыре итерации. Напомним, что для достижения той
же точности при том же начальном приближении методами Якоби и
Зейделя потребовалось соответственно тринадцать и семь итераций.
217

219. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
§ 6.4. Другие двухслойные итерационные методы
Наряду с методами простой итерации, Зейделя и последовательной
верхней релаксации существует большое число иных итерационных
методов, предназначенных для решения систем линейных алгебраи­
ческих уравнений
Ах=Ь. (6.31)
Особенно глубоко разработана теория итерационных методов для
систем с симметричными положительно определенными матрицами.
Рассмотрим некоторые из них.
Всюду в этом параграфе будем считать, что матрица А - симмет­
ричная и положительно определенная. Напомним, что для такой
матрицы все ее собственные значения А. 1 , ••• , А.т положительны. Кроме
того, справедливы неравенства
A.min llxll; -;::; (Ах, х) -;::; A.maJxll; для всех х Е JRт,
A.min llxl/ 2-;::; llAxll 2-;::; A.max llxl/2 для всех х Е IRт,
(6.32)
(6.33)
где A.min и A.max - минимальное и максимальное собственные значения.
Из неравенств (6.32), в частности, следует, что величина llxllA =
= J(Ах, х) является нормой в JRт; эту норму принято называть энерге­
тической. Неравенства (б.33) позволяют увидеть, что llAll 2= A.max,
llA-% = A.~1in И поэтому cond2(A) = llAll2llA-% = A.max/A.min·
1. Двухслойные итерационные методы. Итерационный метод
называют одношаговым или двухслойныw если для вычисления очередного
приближения x(k + 1) к решению х системы (6.31) используется только одно
предыдущее приближение x(k). Например, методы простой итерации,
Зейделя и последовательной верхней релаксации - двухслойные.
Многие двухслойные итерационные методы могут быть записаны в
каноническом виде
x(k+l)_x(k)
В +Ах<*>= Ь k = О, 1, ....
'k- 1
(6.34)
Здесь В - некоторая невырожденная матрица, tk + 1 > О - итераци­
онные параметры. Матрица В может, вообще говоря, зависеть от k, то
есть меняться от итерации к итерации. В случае, когда параметры
tk+ 1 =•(и матрица В) не зависят от номера итерации, метод называют
стационарным.
218

220. § 6.4. Другие двухслойные итерационные методы
Если В = Е - единичная матрица, итерационный метод принимает
вид
x(k+ l) _x(k)
- - - - +Ax<k> = Ь k= О, 1, ".
tk+ 1 '
и называется явным, поскольку в нем очередное приближение явным
образом выражается через предыдущее:
(6.35)
В общем случае, при В '#: Е, метод является неявным, так как на
каждой итерации требуется решать систему уравнений
Bx<k+l)=Bx(k)_тk+ 1 (Ax<k>-b), k=O, , " ..
Конечно, матрица В должна быть такой, чтобы каждая из этих систем
решалась значительно быстрее, чем исходная система (6.31 ). Например,
матрица В может быть диагональной, трехдиагональной, треугольной
или разреженной.
Замечание. При численной реализации неявного метода
(6.34) обычно сначала вычисляется невязка r(k) = Ь - Ax<k>, затем
x(k+l)_x(k)
относительно вектора w<k> = , пропорционального
tk+ 1
поправке к решению, решается система уравнений
вw<k> = r(k)' (6.36)
после чего находится очередное приближениех(k+ I) =x(k) +'k+ 1w(k).
2. Каноническая форма записи методов Якоби, Зейделя и после­
довательной верхней релаксации. Представим матрицу А в виде
суммы А = D + А 1 + А 2, где D - диагональная матрица с диаго­
нальными элементами d11 = а11 для 1 :$ i :$ т, матрица А 1 - нижняя тре-
угольная с элементами а~)> =аlJ для 1 :$ j < i :$ т и а~)> = О для 1 :$ i <
. < А (2)
<1 _ т; наконец, матрица 2 - верхняя треугольная с элементами а,1
= alJ для 1 :$ i < j :$ т и а~}> = О для 1 :$ j < i :$ т.
Рассмотренные в предыдущих параграфах методы могут быть запи­
саны в каноническом виде (6.34). Метод Якоби соответствует выбору В= D
и 'tk + 1 = 1. Метод Зейделя может быть записан в виде (6.34), если взять
В = D + А 1 (т.е. выбрать в качестве В нижнюю треугольную часть
219

221. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
матрицы А) и tk + 1 = 1. Метод последовательной верхней релаксации
соответствует выбору В= D + roA 1 и tk + 1 = ro.
3. Явный стационарный итерационный метод с оптимальным
параметром. Рассмотрим явный стационарный итерационный метод
x(k + 1) = x(k) - t (Ах<*>- Ь), k =О, 1, ... . (6.37)
Как нетрудно видеть, он представляет собой метод простой итерации
x<k+l)=Stx<k>+tb, k=O, 1, ...,
где St = Е - tA - матрица, называемая матрицей перехода. Эrа матрица
симметрична, причем ее собственные значения Л.1 (St) вычисляются через
собственные значения матрицы А по формуле Л.,(St) = 1 - tЛ.,. Поэтому
спектральный радиус матрицы St совпадает с /IStll 2 = llE - tAll2 и вычис-
ляется по формуле p(St) = q(t) = max 11 - tA., I.
15,15,т
В силу теоремы 6.2 метод (6.37) сходится тогда и только тогда, когда
q(t) < 1, причем справедлива оценка погрешности
lix<n>-xil2 :Sq(t)"iix<0>-xil2 , п'?.1.
Скорость сходимости метода зависит от t и она тем выше, чем
меньше величина q(t). Можно показать, что функция q(t) принимает
свое минимальное значение q0 при
2
(6.38)t=t = - - - -
опт лmш + лmах
(В этом смысле выбор параметра (6.38) является оптимальным.) При этом
т.е.
сопd2(А)- 1
q =о сопd2(А) + 1 ·
Таким образом, справедлив следующий результат.
(6.39)
Теорема 6.8. Явный стационарный итерационный метод (6.37)
с оптимальным выбором параметра (6.38) сходится с оценкой
погрешности
lix<">- xil2 :S q~lix<0>-xil 2 , п '?. 1,
где q0 определяется формулой (6.39). •
220
(6.40)

222. § 6.4. Другие двухслойные итерационные методы
Заме чан и е 1. Оценка (6.40) позволяет оценить число итераций,
достаточное для того, чтобы уменьшить начальную погрешность в
нужное число раз, т.е. добиться выполнения неравенства
llx(n>-xll2 sellx<0>-xll2 (6.41)
при фиксированном е > О. Это неравенство выполнено, если q~ s е,
т.е. если
> _ n(/E)
п _ п0 (е) - ( / ) .
ln 1 q0
Замечание 2. Из формулы (6.39) видно, что q0 растет с ростом
2
cond2 (A), причем q0 = 1 - ( ) --+ 1 при cond2 (A)--+ оо. Ta-
cond2 А + 1
ким образом, скорость сходимости метода с ростом числа обуслов­
ленности матрицы А замедляется. Кроме того,
1
п 0 (е) ~ 2 cond2(A)ln(l/e) при cond2(A) » 1. (6.42)
Следует обратить внимание на то, что в прикладных задачах
часто встречаются системы уравнений с матрицами, для которых
число обусловленности cond2 (А) » 1. В таких задачах число ите-
раций, определяемое по формуле (6.42), недопустимо велико.
Замечание 3. Выбор оптимального параметра t00т предпола­
гает знание собственных значений Л.mш и Л.mах· Часто они неизвест­
ны, но имеются их оценки О< µ s Л.mш s Л.mах s М В этой ситуации
2
оптимальным является выбор параметра t опт = - - , а метод схо­
µ + М
М-µ М/µ-1
дится с оценкой (6.38), в которой q0 = -- = / . Кроме того,
М+µ М µ+
1
п 0(е) ~ 2 (М/ µ) ln(l/e) при М/ µ » 1. (6.43)
4. Явный итерационный метод с чебышевским набором пара­
метров. Заметим, что погрешность явного итерационного метода
x<k + IJ = x<k> - tk + 1(Ax<k> _ Ь), k = О, 1, ". (6.44)
удовлетворяет равенству
x(k + 1>- х = S (x<k> - х), k ~О,
'k+ 1
221

223. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
где St = Е - tk + 1А. Поэтому для погрешности, полученной на п-й
k + 1
итерации справедливо равенство
(п) - _ (0) -
х - х - st st ." st (х - х)
п п-1 1
и, как следствие, - оценка
llx(nJ -xll2 ~ qпllx<OJ -xll2,
где qп = llSt St ". St 11 .
п п-1 1 2
Зададимся фиксированным числом итераций п и поставим задачу
выбора таких итерационных параметров t 1, t 2, "., tn, для которых
величина qn минимальна. Известно, что такими параметрами являются
tопт
tk= - - - , k = 1, 2, "., п,
1 + чоµk
где tопт и q0 задаются формулами (6.38) и (6.39), а числа
jk1t
µk=cos-, k=1,2".,п
2п
(6.45)
(6.46)
- это занумерованные в некотором порядке корни многочлена
Чебышева Тп'· Здесь Jn = (j1, j 2, "., iп) - упорядоченный набор
нечетных чисел из множества {1, 3, ..., 2п - 1}, определяющий
порядок, в котором берутся корни.
Метод (6.44) с итерационными параметрами (6.45) называется
явным итерационным методом с чебышевским набором параметров
или методом Ричардсона.
Теорема 6.9. Для явного итерационного метода с чебышевским
набором параметров справедлива оценка погрешности
(6.47)
Jcond2(A)- 1
в которой р = . •
Jcond2(A) + 1
Используя оценку (6.47), определим число итераций, достаточное
для того, чтобы добиться выполнения неравенства (6.41 ), т.е.
уменьшить начальную погрешность в 1/r. раз. Заметим, что неравенство
1 Определение н свойства многочленов Чебышева рассматриваются в § 11.6.
222

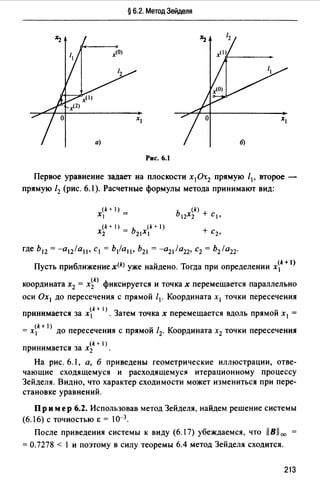
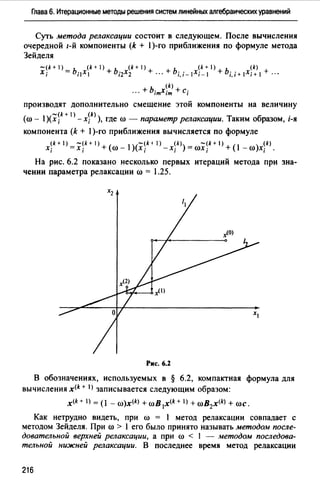
224. § 6.4. Другие двухслойные итерационные методы
-2рп
~ Е выполнено, если р" ~ Е/2. Отсюда п ~ п 0(Е)
1 + р2п
2
Поскольку р = 1- то
JcondiA) + 1'
п 0(Е) ~ ~ Jcond2(A) ln(2/E) при cond2(A) » 1.
In(2/e)
ln(I/p).
(6.48)
Сравнение значения (6.48) со значением п 0(Е), определяемым фор­
мулой (6.42) показывает, что метод с чебышевским набором пара­
метров требует примерно в Jcond2(A) меньшее число итераций, т.е. он
обладает существенным преимуществом в числе итераций перед
методом простой итерации с оптимальным выбором параметра.
Замечание 1. Следует обратить внимание на то, что число ите­
раций п для итерационного метода с чебышевским набором парамет-
ров заранее фиксируется и за приближение к решению х принима­
ется именно х<п>. Значения х<* полученные на промежуточных
шагах с О < k < п, плохо аппроксимируют решение. При необходимо­
сти уточнить приближение цикл из п итераций повторяется, и за сле­
дующее приближение к решению принимается х<2п).
Замечание 2. При п = 1 метод с чебышевским набором пара­
метров превращается в явный стационарный итерационный метод
(6.37) с оптимальным параметром (6.38).
Замечание 3. Метод Ричардсона длительное время не исполь­
зовался на практике из за серьезных проблем с вычислительной
устойчивостью. Как оказалось, для вычислительной устойчивости
рассматриваемого метода очень важен порядок, в котором берутся
нули многочлена Чебышева. Устойчивость метода имеет место
только при специальной нумерации нулей. В противном случае
наблюдается резкий рост вычислительной погрешности, который
может привести к полной потере точности.
В настоящее время известны наборы чисел 1 Jn = (j1, j2, "., jn),
обеспечивающие вычислительную устойчивость метода, и алгоритмы
их построения для любого п. Приведем такие наборы для п = 4, 8, 16.
14 = (1, 7, 3, 5), lg = (1, 15, 7, 9, 3, 13, 5,11),
Jlб = (1, 31, 15, 17, 7, 25, 9, 23, 3, 29, 13, 19, 5, 27, 11, 21).
1 Алгоритмы их построения были опубликованы практически одновре!енно в статье
В.А. Лебедев, С.А. Финогенов // Журн. вычисл. матем. и матем. физ. 1971. Т. 11. № 2.
С. 425-438 и в монографии А.А. Самарский. Теория разностных схем. М.: Наука, 1971.
Дополнительную информацию можно найти также в [62, 89].
223

225. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Замечание 4. Если вместо собственных значений Лmш и Лmах
известны лишь их оценки о<µ~ лm1n ~ лmах ~ М, ТО чебышевский
набор параметров может быть вычислен по формулам (6.45), (6.46)
2 М-µ
с •опт = -- , q0 =-- . Для построенного таким образом метода
µ+ н м+ µ
- Jij/µ-1будет справедлива оценка (6.47), в которои р = г.;-;- . Кроме
-1М/µ+ 1
того, число итераций, достаточное для уменьшения погрешности в
1/i: раз составит
n0(i:),,.iJM/µln(l/i:) при М/µ»1
(ер. с (6.43)).
6. Неявный итерационный метод с оптимальным выбором
параметра. Пусть В - симметричная положительно определенная
матрица. Известно, что существует единственная симметричная поло­
жительно определенная матрица С такая 1 , что С2 =В. Положим у<*>=
= Сх<*> и запишем неявный итерационный метод (6.34) в виде эквива­
лентного явного метода
y<k + 1) - y(k) - -
------'-- +Ау<*>= Ь, k = О, 1, ...,
1 k + 1
где А = с- 1лс- 1 , Ь = с-1 ь.
Поскольку матрицы А и с- 1 - симметричные и положительно
определенные, то и матрица А - симметричная и положительно
определенная. Обозначим через ~min и ~max ее минимальное и макси­
мальное собственные значения. Заметим, что у= Сх является
решением системы Ау= Ь .
Из теоремы 6.8 следует, что явный стационарный итерационный
метод
y(k+ 1) _ y(k) - -
"--~-+Ay<k>=b, k=O, 1, ...,
1
с оптимальным выбором параметра
(6.49)
1 Матрица С называется корнем квадратным иэ матрицы А и обозначается через JA.
224

226. § 6.4. Другие двухслойные итерационные методы
сходится с оценкой погрешности
11/п) - yJl2 $ q~Jl/O) - yll2, n ~ ,
в которой
_ сопd2(А) - 1
qo= - .
сопd2(А) + 1
Как следствие, эквивалентный неявный стационарный метод
x<k+l)_x(k)
в +Ах<k>=ь k=O, , ...t ,
(6.50)
(6.51)
с оптимальным выбором параметра (6.49) сходится с оценкой погреш­
ности
llx<п>_xll2$Jcond2(B) q~llx<0>-xll2, п~ ,
в которой q0 определяется формулой (6.50).
(6.52)
Для того, чтобы этот метод обладал преимуществом в скорости схо­
димости перед явным методом (6.37) с оптимальным выбором пара­
метра, нужно, чтобы число q0 было существенно меньше числа q0, т.е.
нужно выполнение условия cond2(A) « cond2(A).
Матрицу В, гарантирующую существенное уменьшение числа обу­
словленности, часто называют предобусловливателем 1, а процесс ее
построения - предобусловливанием. Предобусловливание является
весьма сложным делом, поскольку предобусловливатель В обязан
обладать еще одним важным свойством: он должен иметь такую
структуру, чтобы системы вида (6.36) решались достаточно быстро.
Как правило, найти собственные значения матрицы А = c-IAC- 1
являющиеся решениями обобщенной задачи на собственные значения
Ах= Л.Вх, весьма сложно. Значительно проще найти оценки µ1 и М1
минимального и максимального собственных значений: о< µ1 $ rm1n $
$ rmax $ М1 или, ЧТО то же самое, - найти числа о < µ1 $ М1 такие, что2
µ 1(Вх, х) $ (Ах, х) $ М1 (Вх, х) для всех х Е Rm. (6.53)
1 Иногда ее называют переобуславливателе.w.
2 Матрицы В н А, связанные неравенством (6.53), называют спектрально эквивалент­
ны.wи или энергетически эквивалентныwи.
225

227. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
В этом случае можно использовать итерационный метод (6.51) с
2
t= - - , (6.54)
µ, +м,
для которого справедлива оценка погрешности (6.52) с
_ М1 -µ 1 М1 /µ 1 -1
Чо = - - = . (6.55)
М1 +µ 1 М/µ 1 +1
Замечание. Следует подчеркнуть, что для реализации метода
(6.51) нет необходимости в вычислении матриц С и А. Они нужны
лишь для теоретического исследования свойств метода.
6. Неявный итерационный метод с чебышевским набором пара­
метров. Аналогичные соображения приводят к пониманию того, что
в неявном методе (6.34) с симметричной положительно определенной
матрицей В возможен выбор чебышевского набора параметров
'опт
tk= - • k= 1,2, ...,п,
1 + чоµk
(6.56)
в котором tопт• q0 и µk вычисляются по формулам (6.49), (6.50)
и (6.46). Этот метод представляет собой неявный итерационный метод
с чебышевским набором параметров. Для него справедлива оценка
погрешности
(6.57)
_ JrondiA)- 1
в которой р = -;::=::::::;;;=--
Jcond2(A) + 1
Если вместо значений ):.m•n и ):.max известны лишь их оценки О < µ1 ~
~ im•n ~ ):.max ~ М1, удовлетворяющие неравенству (6.53), то в формуле
2 - м, -µ,
(6.56) следует взять tопт =--- , q0 =--- . Для метода (6.34) с
µ, + м, м, + µ,
таким набором параметров будет справедлива оценка погрешности
~-
(6.57) с р = - - - -
Jм, 1µ,+1
Конечно, при реализации неявного метода с чебышевским набором
параметров необходимо использовать порядок выбора нулей много­
члена Чебышева, гарантирующий вычислительную устойчивость.
226

228. § 6.4. Друmе двухслойные итерационные методы
7. Методы минимальных невязок и поправок. Запишем двух­
слойный итерационный метод (6.35) в виде
(6.58)
где r(k) = Ь - Ах<*> - невязка, полученная на k-й итерации. Умножив
слева обе части равенства (6.58) на -А, получим соотношение
(6.59)
Выберем параметр t k + 1 таким образом, чтобы минимизировать евк­
лидову норму невязки llr<k+l)ll 2 =llr<*>-tн 1Ar<*>ll 2 • Заметим, что
функция
k 2 *2 k 2 2<p(tk+ 1) = llr< >-tk+ 1Ar<*>ll2= llr< Ъ-2tk+ 1(Ar<*>, r< >) + •k+ 1llAr<*>ll2
является квадратичной по '* + 1 и достигает своего минимума при зна­
чении
(Ar<*>, r<*>)
't =
k+ 1 llAr<*>ll~ .
(6.60)
Теорема 6.10. Для метода минимальных невязок (6.58)-(6.60)
справедлива оценка
(6.61)
где q0 определяется формулой (6.39). Как следствие, метод сходится
с оценкой погрешности
llx<п> - xll2 s cond2(A) q~llx<0> - xll2, п ~О. (6.62)
Доказательство. В силу специального выбора параметра '* + 1
справедливо неравенство
llr<* + 1)112 = ll(E - •н 1A)r<*>ll2=min ll(E - tA)r<*>ll2 S ll(E - •on~)r<*>ll 2.
t>O
Принимая во внимание, что llE- •оп~11 2 =q0 (см. п. 3), имеем
llr<k+ 1 Ъ S llE - •0nтA11 2 llr<*>il2 =Чollr<*>ll2, k ~О.
Как следствие, справедлива оценка (6.61 ).
Поскольку llr<п>ll 2 = llA(x<п> - x)ll2, то
лm1n llx(n) - х 112 s llr<п>112' llr<0>112 s Лma,.llx(O)
и неравенство (6.62) следует из неравенства (6.61). •
227

229. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
3а меч ан и е Метод минимальных невязок сходится с той же
скоростью, что и явный итерационный метод с оптимальным выбо­
ром параметра Однако он обладает тем существенным преимуще­
ством, что не требует для своей реализации знания собственных
значений Л.min и Л.mах или их оценок
Неявный итерационный метод
x<k+ 1) =x<*J + tk+ 1w<*>, Bw<k) = Ь-Ах<*>, k =О, 1, ...,
являющийся аналогом метода минимальных невязок, называется
методом минимальных поправок. В этом методе итерационные пара­
метры вычисляются по формуле
(А w<*>, w<k>)
"tk+I = (в-IAw<k>,Aw<k>)' k= О, 1, ...,
а очередное значение поправки по формуле
w<k+ 1) = w<k>-"tk+ iB-'Aw<k>
Если матрицы А и В спектрально эквивалентны, т.е. связаны нера­
венством (6.53) с О < µ 1 < М1 , то для метода минимальных поправок
справедлива оценка
- м, -µ,
где q0 =--- . Как следствие, справедлива оценка поrр'еmвосrи
м,+µ1
llx<nJ - xll2 ~с q~llx<0> -xll2, п?. 1,
где с= Jcond2(B) (М1 /µ 1 )
8. Метод наискорейшего спуска. Покажем, что задача решения
системы уравнений (6.31) с симметричной положительно опреде­
ленной матрицей А эквивалентна задаче поиска точки минимума квад­
ратичной функции
1
F(x) = 2 (Ах, х) - (Ь, х). (6.63)
Действительно, пусть х - решениесистемы (6.31). Тогда для х =
= х + Лх при Лх * О имеем
228

230. § 6.4. Друrие двухслойные итерационные методы
- 1 - - 1 -- -
F(x)-F(x) = '2 (А(х + ЛХ), х + ЛХ)-(Ь,х)- 2 (Ах, х) + (Ь, х) =
- 1 - - 1 - -
=(Ах -Ь, Лх) + '2 (АЛх, ЛХ)=l (АЛх, ЛХ) >О.
Таким образом, всякий итерационный метод минимизации квадра­
тичной функции (6.63) одновременно .являете.я итерационным методом
решени.я системы (6.31). Например, метод покоординатного спуска,
примененный к функции (6.63), дает ту же последовательность прибли­
жений, что и метод Зейдел.я. Подробнее об этом будет сказано в § 10.2;
см. также [9].
В методе наискорейшего спуска итерации осуществляются по тем
же формулам
x<k + 1>=x<k> + 'tk + 1r(k), r<k+ I) = r<k> - 'tk+ 1 А r<k>, k?:. О, (6.64)
что и в методе минимальных нев.язок. Но параметр 'tk + 1 вычисляете.я
иначе:
llr<k>ll~
'tk + 1 = (Ar<k), r<k>).
(6.65)
Именно при этом значении достигает минимума функция <pk(a) =
= F(x<k> + ar<k>) (см. § 10.3).
Теорема 6.11. Метод наискорейшего спуска (6.64), (6.65) сходится
с оценкой погрешности
llx(n) -.XllA s q~llx(OJ -.XllA, п?:. 1,
где q0 определяется формулой (6.39). Как следствие,
llx(n) _.Xll2 s Jcond2(A) q~llx(O) -.Xll2, п?:. 1. •
(6.66)
Замечание 1. Как и метод минимальных невязок, метод наис­
корейшего спуска сходится с той же скоростью, что и явный ите­
рационный метод с оптимальным выбором параметра. Однако он
обладает тем существенным преимуществом перед явным итера­
ционным методом с оптимальным выбором параметра, что не тре­
бует для своей реализации знания собственных значений Лmш
и лmах или их оценок.
Заме чан и е 2. Дополнительную информацию о методе наиско­
рейшего спуска можно найти в § 10.3.
229

231. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
§ 6.5. Метод сопря•енных rрадиентов
1. Метод сопряженных градиентов. 1 Совместная статья Хестенса
и Штифеля2 появилась в 1952 году после того, как они независимо
открыли метод сопряженных градиентов.
Первоначально этот метод рассматривался как один из прямых мето­
дов решения систем линейных алгебраических уравнений
Ах=Ь
с самосопряженными положительно определенными матрицами
порядка т.
Было доказано, что в точной арифметике этот метод дает точное
решение за т шагов. Однако на практике точная сходимость за т шагов
не наблюдалась, поэтому метод сопряженных градиентов расценили как
неустойчивый и интерес к нему на многие годы был утрачен: Только
после того, как в 1971 году Рейд3 продемонстрировал значимость
метода сопряженных градиентов как итерационного метода решения
систем с разреженными матрицами, началось его широкое применение.
В настоящее время метод сопряженных градиентов по праву рассматри­
вается как один из наиболее эффективных итерационных методов реше­
ния систем уравнений с самосопряженными положительно определен­
ными матрицами.
Рассмотрим этот метод. Пустьх<0> - начальное приближение к реше­
нию, r(O) == Ь -Ах<0> - начальное значение невязки ир(О) = r<0>. Прибли­
жения x<k + I) и невязки r<k + I) = Ь - Ax(k + I) при k ~ О вычисляются по
следующим формулам:
r<k+ I) = ,щ - akAp<k),
llr(k+ 1 111~
~ =---k llr(k)ll; .
(6.67)
(6.68)
(6.69)
1 В § 10.3 метод сопряженных граднентов рассматривается как lетод минимизации
квадратичной функции (6.63). Там же можно найти объяснение названия метода.
2 Hestenes M.R" Stiefel Е. L. Methods of conjugate gradients for solving linear systems //
J. Res. Nat. Bur. Stand" Section В. 1952. V. 49. Р. 409---436.
3 Reid J .К. Оп the method ofconjugate gradients for the solution oflarge sparse systems of
1inear equations ff 1n: J. К. Re1d, editor. Large Sparse Sets of Linear Equations, Academic Press.
1971. рр. 231-254.
230

232. § 6.5. Метод сопряженных градиентов
Теорем а 6.11. Справедлива следующая оценка погрешности
метода сопряженных градиентов:
!!х(п) - xl!A ~ ~ l!x(O) - xllA
1+ p2n '
Jcond2(A )- 1
где Р = ~===-- .Как следствие, справедлива oчeнltQ
Jcond2(A) + 1
llx(n)_xll2~Jcond2(A) 2 Рп2 llx<0>-xll2·. 8
1 + р п
(6.70)
(6.71)
Скорость сходимости метода сопряженных градиентов та же, что и у
явного итерационного метода с чебышевским набором параметров, но
в отличие от последнего для его реализации не нужна информация
о значениях лmlП и лmах.
Интересно, что метод сопряженных градиентов имеет все черты
быстро сходящегося итерационного метода, но в то же время он
является и прямым (точным) методом.
Теорема 6.12. Метод сопряженных градиентов позволяет найти
точное решение системы Ах = Ь с симметричной положительно опре­
деленной матрицей порядка т не более чем за т итераций. •
Хотя теоретически одно из приближений х<п> с номером п ~ т
должно совпасть с точным решением х, на практике при решении
систем высокого порядка т этим свойством не удается воспользо­
ваться. Во первых, получение точного решения невозможно из-за
вычислительной погрешности. Во-вторых, как правило, для систем
большого порядка т применение итерационного метода целесообразно
только, если требуемое число итераций п много меньше т.
2. Сверхлинейная скорость сходимости. Классическая априорная
оценка (6.70), казалось бы, указывает на то, что метод сопряженных
градиентов обладает линейной скоростью сходимости. Однако эта
оценка часто бывает чрезмерно пессимистичной и не объясняет тонких
свойств сходимости, присущих методу сопряженных градиентов.
Для метода с линейной скоростью сходимости отношение
lk(k+ ) - xllA
qk = llx(k) _:жllA практически не меняется с ростом k. Тем не менее,
опыт применения метода сопряженных градиентов показал, что это
отношение обычно убывает с ростом k, и в ходе итерационного про­
цесса наблюдается ускорение скорости сходимости метода.
231

233. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Первое объяснение этого эффекта, получившего название сверхли­
нейной сходимости, на качественном уровне было дано в 1976 г. 1 В
1986 г. Вандерслюис и Вандерворст2 дали его теоретическое обоснова­
ние. Оказалось, что метод сопряженных градиентов (в точной арифме­
тике) через некоторое время начинает вести себя так, будто в матрице А
исчезли крайние собственные значения Л 1 = Лmш(А) и Л" = ЛmaiA);
затем - так, будто исчезли собственные значения Л2 и Л" _1 и так далее.
Таким образом, влияние крайних собственных значений сказывается
только на первых итерациях и существенным оказывается распределе­
ние основной части собственных значений.
Исследование феномена сверхлинейной сходимости продолжается.
3. Метод сопряженных граднеюов с предобусловлнваннем. Метод
сопряженных градиентов сходится очень быстро, если cond2(A) "" 1.
Напротив, метод сходится довольно медленно, если cond2 (A) » 1.
Поэтому возникает естественное желание выполнить предобусловли­
вание - заменить исходную систему уравнений Ах= Ь эквивалентной сис­
темой
Ау=Ь (6.72)
с матрицей А , число обусловленности которой много меньше числа
обусловленности матрицы А.
Пусть В - некоторая невырожденная матрица. Положим у = Вх и
умножим слева левую и правую части системы Ах = Ь на (Вт)-1 •
В результате получится система (6.72), в которой А = (ВТ)-1АВ- 1 , Ь
= (BT)-lb.
Заметим, что построенная таким образом матрица А - симмет­
ричная и положительно определенная. Если cond2(A) « cond2(A), то
имеет смысл применить метод сопряженных градиентов (6.67Н6.69)
к преобразованной системе. Пусть у<0> - начальное приближение,
q<0>= s<0>, где s<O> = Ь -Ау<0> - начальное значение невязки. Прибли-
1 Concus Р, Golub G.H" O'Leary D.P. А generalized conjugate gradient method for the
numerical solution ofelliptic partial differential equations // In:J.R. Bunch and D.J.Rose, editors,
Sparse Matr1x Computatюns Academ1c Press, New York. 1976.
2 Van der Slu1s А" van der Vorst Н.А. The rate of convergence of conjugate gradients //
Numer. Math .1986. V. 48. рр. 543-560.
232

234. § 6.5. Метод сопряженных градиентов
женияу<kJ к решению и невязки s<kJ = Ь -Ay<k> при k ~ 1 вычисляются
по формулам:
s<k+ 1) = s<kJ _ akAq<kJ,
iis(k+ l)jj~
13 =---
k lls<kJll; .
Используя теперь формулы связи y(k) = Bx<~J. s<kJ = (BT)-lr(k), q(k) =
= Вр (k), приходим к методу сопряженных градиентов с предобуслов-
ливанием:
, (О) = ь -А.х(О), втs(О) =,(О), Вр(О) = s<O>,
lls<k>ll~
x<k + 1) =x<k> + akp<k>, а = - - - -
k (Ap<k>, p<k>)'
r<k+ 1) = ,щ - akAp<k>,
вrs(k+l)=r<k+I), B:z(k+l)=s<k+I>,
lls<k+ 1>11;
p<k + 1) = :z<k + 1) + 13kp(k), 13 = ___
k lls<k>ll; .
(6.73)
(6.74)
(6.75)
(6.76)
(6.77)
Теорема 6.13. Для метода сопряженных градиентов с предобу­
словливанием (6.73Н6.77) справедливы оценки погрешности (6.70),
Jcond/A)-1
(6.71) с р= - .•
Jcond2(A) + 1
Обратим внимание на то, что платой за ускорение сходимости
методе стала необходимость решать на каждой итерации системы
(6.76). Поэтому эффективность работы метода самым существенным
образом зависит от того, как быстро могут решаться эти системы.
Нет общего рецепта, как построить предобусловливатель В. Более
того, его построение предполагает выполнение противоречивых свойств.
С одной стороны, матрица В должна быть такой, чтобы величина
cond2(A) была, по возможности, минимальной. В этом смысле иде­
альным был бы выбор В = LТ, где L - невырожденная нижняя тре­
угольная матрица, входящая в разложение Холецкого А= LLт (см.§ 5.8).
233

235. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
При таком выборе А = Е, cond2(A) = 1 и метод сопряженных гради­
ентов даст точный результат за один шаг. Однако, если мы уже имеем
матрицу L и можем быстро решать системы вида LTy = Ь, Lx =у, то в при­
менении итерационного метода нет необходимости.
С другой стороны, необходимо, чтобы структура матрицы В была
достаточно простой, чтобы быстро решать системы (6.76).
Ясно также, что вычисление предобусловливателя В не должно тре­
бовать большой вычислительной работы.
Одна из наиболее важных стратегий предобусловливания состоит в
использовании неполного разложения Холецкого, в котором вт= i -
аппроксимация матрицы L, входящей в разложение Холецкоrо.
Простой метод вычисления L указан в [31).
Замечание. Свойство сверхлинейной сходимости (см. п. 2)
подсказывает и другую стратегию предобусловливания. Предобус­
ловливатель нужно выбирать не так, чтобы число обусловленности
матрицы А было много меньше числа обусловленности матрицы
А, а так, чтобы большая часть собственных значений матрицы А
сконцентрировалась (кластеризовалась) вблизи единицы, то есть в
интервале (1 - Е1' 1 + е2). Если вне этого интервала окажется лишь
небольшой набор собственных значений, то после нескольких ите­
раций метод сопряженных градиентов начнет вести себя так, как
1+е 1
будто число обусловленности матрицы А не превышает
) - Е2.
При этом возможно, что даже cond2(A) > cond2(A).
§ 6.6. Допоnнитеnьные замечани•
1. В этой главе были рассмотрены лишь основные итерационные
методы решения систем линейных алгебраических уравнений. -Вне
нашего поля зрения остались многие известные и популярные методы.
Среди них методы расщепления (неявные методы переменных направ­
лений), блочные итерационные методы, методы подпространств
Крылова, метод сопряженных невязок, обобщенный метод мини­
мальных невязок (GMRES), методы MINRES, QMR, Bi-CGSTAB.
Эrи методы изложены, например, в учебниках [9, 88, 100, 122, 2°, 5°,
16*] и в специальной литературе [24, 89, 110, 121, 123, 24°, 26°].
234

236. § 6.6. Дополнительные замечания
2. В гл. 1О мы еще раз вернемся к методам наискорейшего спуска и
сопряженных градиентов в связи с задачей минимизации квадратичной
функции (6.63). Обсуждение некоторых интересных особенностей
метода сопряженных градиентов можно найти в [100, 5*], см. также [31].
3. В настоящее время наиболее глубоко развиты методы решения
систем уравнений с симметричными положительно определенными
матрицами. Однако часто встречаются задачи, в которых матрица А -
несимметричная или симметричная, но не является положительно
определенной. Ряд эффективных методов решения систем уравнений
с несимметричными матрицами рассмотрен в [89, 110, 122, 123, 2*, 26*].
В принципе, всегда существует возможность симметризовать любую
систему Ах = Ь с невырожденной матрицей, т.е. свести ее к эквива­
лентной системе с симметричной положительно определенной мат­
рицей. Для этого достаточно умножить обе части системы на матрицу
Ат. В полученной таким образом системе
АТА.х =Ать (6.78)
матрица А = АТА обладает всеми нужными свойствами. Однако, как
правило, это делать не рекомендуется. Дело в том, что при переходе от А
к А может быть потеряно свойство разреженности. Как следствие, воз­
растут вычислительные затраты на одной итерации. Кроме того, как
правило, существенно ухудшается обусловленность системы. Например,
для матриц, близким к симметричным, cond(A)"" (cond(A))2 . В силу
этого даже самые быстрые методы решения систем с симметричными
матрицами в применении к системе (6.78) могут стать очень неэффек­
тивными.
4. Как уже было отмечено, одно из важнейших достоинств итераци­
онных методов заключается в возможности эффективного использо­
вания разреженности матрицы системы. Поясним сказанное на примере
метода простой итерации (6.6).
В случае, когда матрица В - заполненная, для вычисления по
формуле (6.6) требуется выполнить примерно 2т2 арифметических
операций. Однако для разреженной матрицы с М (М « т2) нену­
левыми элементами требуется лишь примерно 2М арифметических
операций (одно умножение и одно сложение на каждый ненулевой
элемент). Таким образом, общее число операций составляет примерно
2Мп(Е), где n(E) - число итераций, необходимое для достижения
заданной точности Е.
5. В случае, когда препятствием для быстрой сходимости итераци­
онного метода является плохая обусловленность матрицы А, для уско­
рения сходимости систему Ах = Ь заменяют эквивалентной системой
- - - -1 -1
Ау= Ь с матрицей вида А= В1 АВ, , которая имеет существенно
меньшее число обусловленности. Этот подход, называемый предобу­
словливание.м, уже обсуждался в § 6.4.
235

237. Глава 6. Итерационные методы решения систем линейных алгебраических уравнений
Как правило, матрицу А явным образом не вычисляют, используя
в итерационном процессе наряду с исходной матрицей А невырожденные
матрицы В1 и Br, которые называют левым и правым неявным пред­
обусловливателями. Неявными предобусловливатели называют потому,
-1
что их использование сводится к вычислению векторов вида w = 8 1 z,
-1
w = Вr z, т.е. к решению систем В1w = z, В r w = z. Если в преобразо-
ванной системе матрица А имеет вид А = B1ABr, то предобусловли­
ватели называются явными, так как их применение сводится к явному
умножению В1 и В, на соответствующие векторы. Возможны варианты
- -1 - -1
А= В1 ABr или А= в,Авr , когда ОДИН из предобусловливателей
является явным, а другой неявным. Часто один из предобусловлива­
телей отсутствует; это не противоречит общей ситуации, а означает,
что В1 = Е либо Вr = Е.
При построении неявного метода с оптимальным параметром (6.51)
теоретически система Ах = Ь преобразовывалась к эквивалентной
системе с матрицей А= с-1 АС-1 , где С= .[В играет роль левого и
правого неявного предобусловливателей. Однако при численной реали­
зации метода фактически система преобразуется к виду в-1 Ах = в-1 Ь,
т.е. роль неявного левого предобусловливателя играет матрица В, а
правый предобусловливатель отсутствует. Так же используются предобу­
словливатели в неявном методе с чебышевским набором параметров.
В методе сопряженных градиентов с предобусловливанием исполь-
зуется преобразование к виду (6.72), где А= (ВТ)-1АВ-1 , т. е. оба пред­
обусловливателя В1 = вт и Br = В - неявные. Важно то, что матрица
А = (BT)-IAB- 1 - симметричная и положительно определенная, если
исходная матрица А - симметричная и положительно определенная.
Обычно неявные предобусловливатели 8 1 и Br выбираются так,
чтобы системы уравнений с ними легко решались. В то же время жела­
тельно, чтобы в определенном смысле матрица А была как можно
ближе к единичной матрице Е, т.е. матрица B1Br в некотором смысле
должна приближать матрицу А.
6. Иногда, используя информацию о уже полученных прибли­
жениях к решению, удается построить уточненное приближение без
существенных дополнительных вычислительных затрат.
Пусть, например, х<п - 2>, х<п - l) и х<п) - три последовательных при­
ближения, полученных с помощью стационарного двухслойного итера-
236

238. § 6.6. Дополнительные замечания
ционного метода. Согласно о2-процессу ускорения сходимости уточ­
ненное приближение х(п) имеет ВИД
_( ) ( ) х(п) _ х<п - 1)
xn =хп +----
1 -уп
(х<п- ) _х(п-2),х(п)_х(п-1))
Уп= llx<п>-x<n-IJ!j; .
Приближение х(п) может быть использовано далее как начальное ДЛЯ
следующих итераций. Как критерий применимости о2-процесса может
быть использовано приближенное равенство
1(х<п-1) -х<п -2), х<п) _х<п - 11) 1
"" l.llx<n - 1) - х<п -2>1i 2lix<n) - х<п - 1>ii2
Подробнее о о2-процессе см. в [9].
Приближения х<п - 2>, х<п - I) и х<п> могут быть использованы и иначе.
Будем искать уточненное приближение к решению в виде
,Х<п> =х<п-2) + а(х<п-l)_х(п-2)) + р(х<п>-х<n-2>), (6.75)
где параметры а и р определяются из условия минимума евклидовой
нормы невязки ;:<п> =Ь-Ах<11>. Заметим, что
;<п> =,.<11-2) +алr<п-1) + рл,.<п)'
где r<п> =Ь -Ах<п>, лr<п-1) =r<п-1) _ r<п-2>, лr<п> =r<п> _r<п-2).
Необходимое условие экстремума для функции
ср(а, р) = lir<11 - 2>+ алr<п-I) + рлr<11>11~.
приводит к системе уравнений
(Лr<п-1>, лr<n- l))a + (Лr<п-1>, лr<п>)р =-(r<п-2>, дr<п-1>),
(Лr<11 - 1>, лr<11>)а + (Лr<11>, Лr<11>)р =-(r<п-2>, Лr<11>)
относительно параметров а и р. Найденное приближение (6.75) таково,
что
11r<11>il2 s min{11 r<11 - 2ъ, 11r<11 - 1>112, 11r<11>ll2} .
Дальнейшее развитие этой идеи приводит к обобщенному методу
минимальных невязок (MINRES).
237

239. Глава 7
МЕТОДЫ ОТЫСКАНИЯ РЕШЕНИЙ
СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе рассматривается задача отыскания решений систем
нелинейных уравнений, существенно более сложная, нежели задачи
отыскания решения одного нелинейного уравнения или системы
линейных алгебраических уравнений. Тем не менее достаточно под­
робное знакомство с содержанием гл. 4 и 6, а также § 5.1-5.3
позволяет увидеть соответствующие аналогJ.fи в постановках проблем и
методах их решения для нелинейных систем.
Будем считать, что в множестве т-мерных векторов введена неко­
торая норма, порождающая соответствующую норму для квадратных
матриц порядка т (см. § 5.2).
§ 7. 1. Постановка задачи. Основные этапы реwения
1. Постановка задачи. Задача отыскания решения системы неJJR­
нейных уравнений с т неизвестными вида
f1(X1,X2, ...,xm)=O,
/2(Х1, Х2, ... , хт) =О,
(7.1)
fm(X1, Х2, ..., Хт) = 0
является существенно более сложной, чем рассмотренная в гл. 4 задача
отыскания решения уравнения с одним неизвестным. Однако на
практике она встречается значительно чаще, так как в реальных иссле­
дованиях интерес представляет, как правило, определение не одного, а
нескольких параметров (нередко их число доходит до сотен и тысяч).
Найти точное решение системы, т.е вектор х = (х 1 , х2, ••• , хт)т, удов­
летворяющий уравнениям (7.1 ), практически невозможно. В отличие от
случая решения систем линейных алгебраических уравнений использо­
вание прямых методов здесь исключается. Единственно реальный путь
решения системы (7.1) состоит в использовании итерационных методов
для получения приближенного решениях = (х~, х;, ..., х~)т, удовлетво-
ряющего при заданном е > О неравенству llx' - х 11 < е.
238

240. § 7.1. Постановка задачи. Основные этапы решения
Прежде чем перейти к изучению методов решения системы (7.1 ),
подчеркнем важность понимания того факта, что эта задача может
вообще не иметь решения, а если решения существуют, их число может
быть произвольным. В общем случае весьма сложно выяснить, имеет
ли система решения и сколько их.
Пр им ер 7.1. Рассмотрим систему уравнений
2 2
4х 1 +х2 =4,
2
Х1 - Х2 + t = О.
Здесь х 1 , х2 - неизвестные; t - параметр.
Первое уравнение задает на плоскости х1 0х2 эллипс, второе урав­
нение - параболу. Координаты точек пересечения этих кривых дают
решения системы. Если значения параметра t изменяются от -2 до 2, то
возможны, например, следующие ситуации (рис. 7.1):
а) t = -2 - решений нет; б) t = -1 - одно решение;
в) t = О - два решения; r) t = 1 - три решения;
д) t = 2 - четыре решения. А
о
а)
Рис. 7.1
239

241. Глава 7. Методы отыскания решений систем нелинейных уравнений
Для дальнейшего удобно использовать сокращенную векторную
форму записи систем. Наряду с вектором неизвестных х = (х1, х2, •.. , хт)т
рассмотрим вектор-функцию/= (f, h, ...,fт)Т. В этих обозначениях
система (7.1) примет вид
/(х) =О. (7.2)
Будем считать функции f, (х) непрерывно дифференцируемыми в
некоторой окрестности решения х. Введем для системы функций/.,, h,
...,fm матрицу Якоби
д/1 (х) д/1 (х) дf1(х)
дх1 дх2 дхт
дf2(х) д/2(х) дf2(х)
/'(х) = дх1 дх2 дхт (7.3)
....................
дfт(х) дfт(х) дfт(х)
дхl дх2 дхт
которu будет использована в дальнейшем.
2. Основные этапы решения. Как и для уравнения с одним неиз­
вестным (см. гл. 4), отыскание решений начинают с этапа локализации.
Для каждого из искомых решений х определяют множество, содер­
жащее только одно это решение и расположенное в достаточно малой
его окрестности. Часто в качестве такого множества выступает парал­
лелепипед или шар в т-мерном пространстве.
Иногда этап локализации не вызывает затруднений; соответствующие
множества могут быть заданными, определяться из физических сообра­
жений, из смысла параметров х; либо быть известными из опыта
решений подобных задач. Однако чаше всего задача локализации
(в особенности при больших m) представляет собой сложную проблему,
от успешного решения которой в основном и зависит возможность
вычисления решений системы (7. l). На этапе локализации особое зна­
чение приобретают квалификация исследователя, понимание им
существа решаемой научной или инженерной проблемы, опыт решения
этой или близких задач на компьютере. Во многих случаях полное
решение задачи локализации невозможно и ее можно считать решенной
удовлетворительно, если для х удается найти хорошее начальное при-
240

242. §7.1. Постановка задачи. Основные этапы решения
ближение x<0J В простейших ситуациях (например, для системы двух
уравнений с двумя неизвестными) могут быть использованы графи­
ческие методы (см. пример 7.1)
На втором этапе для вычисления решения с заданной точностью Е
используют один из итерационных методов решения нелинейных систем.
Будем считать, что определения § 4.1, связанные с характеризацией
сходимости итерационных методов, остаются в силе, причем в нера­
венствах (4.5) и (4.6) знак модуля заменен на знак нормы, а о-окрест-
ность решения х понимается как множество точек х, удовлетво­
ряющих условию llx - х 11 < о.
Пример 7.2. Произведем локализацию решений системы
3 3
Х1 + Х2 = 8Х1Х2,
(7.4)
х 1 lnx2 =х2 lnx1•
На плоскости х10х2 построим графики уравнений системы. График
первого уравнения - это лист Декарта 1 (рис. 7.2, а). График второго
уравнения состоит из луча - биссектрисы первого координатного угла
и кривой, пересекающей эту биссектрису в точке (е, е)Т (рис. 7.2, б).
Из рис. 7.3 видно, что эти кривые пересекаются в трех точках А, В, С,
т.е. система имеет три решенИJ1. Так как оба графика симметричны относи­
тельно прямой х1 = х2, то координаты точки В равны и их легко вычислить:
4
2
х
Рис. 7.:Z
1 Рене Декарт (1596-1650) - французский философ, математик, физик, физиолог.
Впервые ввел понятие переменной величины и функции. В аналитической геометрии соз­
дал метод прямоугольных координат.
241

243. Глава 7. Методы отыскания решений систем нелинейных уравнений
Рис. 7.3
х1 = 4, х2 = 4. В силу этой же симметрии достагочно определить только
координаты х 1, х2 точки С, так как точка А имеет координаты х1 = х2 и
х2 = х 1 • Из рис. 7.3 замечаем, что точка С содержится в прямоугольнике
П= {(х,у): 3.5 Sx1 s4, 1.5 sx2 $ 2.5} и х 1 ~ 3.8, х 2 ~ 2. •
Подчеркнем, что только по виду уравнений системы (7.4) без исполь­
зования графического метода установить число решений и найти прибли­
жения к ним было бы весьма трудно. К сожалению, при числе уравнений
т > 3 геометрические иллюстрации теряют свою эффективность.
Замечание. Иногда удается понизить порядок т системы,
выразив одно или несколько неизвестных из одних уравнений сис­
темы и подставив соответствующие выражения в другие уравнения.
Пример 7.3. Система уравнений
х3 + у3 = 8.ху,
xny = lnx
сводится к одному нелинейному уравнению х3 + x3lx = 8xl +llx после
того, как из второго уравнения выражается у= xl1r_ •
3. Корректность и обусловленность задачи. Будем считать, что
система (7.l) имеет решение х, причем в некоторой окрестности этого
решения матрица Якоби f' (х) невырождена. Выполнение последнего
условия гарантирует, что в указанной окрестности нет других решений
системы (7.1 ). Случай, когда в точке х матрица f (х) вырождена,
242

244. § 7.2. Метод простой итерации
является существенно более трудным и нами рассматриваться не будет.
В одномерном случае первая ситуация отвечает наличию простого
корня уравнения /(х) =О, а вторая - кратного корня.
В § 4.2 было показано, что погрешность вычисления функции/ при­
водит к образованию вокруг корня уравнения /(х) = О интервала неоп­
ределенности, внутри которого невозможно определить, какая из точек
является решением уравнения.
Аналогично, погрешности в вычислении вектор-функции/приводят
к появлению области неопределенности D, содержащей решение х
системы (7.1) такой, что для всех х Е D векторное уравнение /(х) = О
удовлетворяется с точностью до погрешности. Область D может иметь
довольно сложную геометрическую структуру (рис. 7.4). Мы удовле-
творимся только лишь оценкой радиуса Е этой области.
Рис. 7.4
Предположим, что для близких к х значений х вычисляемые зна­
чения j (х) удовлетворяют неравенству llЛ:x)-/.(x)ll -5. Л(/0 ).
Тогда Е можно приближенно оценить с помощью неравенства
Е ~ ll(f'(x))-1llЛ(/"). Таким образом, в рассматриваемой задаче роль
абсолюrного числа обусловленности играет норма матрицы, обратной
матрице Якоби f (х ).
§ 7.2. Метод простой итерации
1. Описание метода. Предположим, что требуется найти решение
х = (х1. Х2, ..., хт)Т системы (7.1) с заданной точностью Е >о. Преоб­
разуем систему (7.1) к следующему эквивалентному виду (к виду,
удобному для итераций):
Х1 =(/)1(Х1,Х2, •.. ,хт),
Х2 = (/)2(Х1, Х2, ••. , хт),
(7.5)
243

245. Глава 7. Методы отыскания решений систем нелинейных уравнений
Если ввести вектор-функцию q> = (q>1, ip2, "" ч>т)т, то система (7.5)
запишется так:
х = <р(х). (7.6)
(О) (О) (О) (0) Т
Пусть начальное приближение х = (х 1 , х2 , •• " хт ) задано.
Подставляя его в правую часть системы (7.6), получаем хО> = <р(х<0>).
Подставляя х< 1 > в правую часть (7.6), находим х<2> = <р(хО>) и т.д. Про­
должая вычисления по формулам
x<k + I) = q>(x<k>), k ~ О, (7.7)
получаем последовательность х<0>, хО>, .", х<п>, приближений к
решению х.
Запись (7.7) означает, что очередное приближение x<k + 1> вычис­
ляется через предыдущее приближение x<k> следующим образом:
(k+ ) - ( (k) (k) (k)
х 1 -<р 1 Х1 ,Х2 , ".,Хт ),
(k+ 1) _ ( (k) (k) (k)
Х2 -q>2 Х ,Х2 '".,х,,, ),
(k+ 1) - ( (k) (k) (k)
х,,, -q>,,, Х ,Х2 , ".,Х,,, ).
Отметим существенную аналогию с методами простой итерации для
решения одного нелинейного уравнения (см. гл. 4) и системы линейных
алгебраических уравнений (см. гл. 6).
1. Сходимость метода. Пусть q>'(x) - матрица Якоби, отвечающая
вектор-функции q>(x) (см. § 7.1 ). Сформулируем теорему о сходимости
метода простых итераций, являющуюся аналогом теорем 4.2 и 6.1.
Теорема 7.1. Пусть в неl(()торой а-окрестности решения .i
функции q>,(x) (i = 1, 2, "., m) дифференцируемы и выполнено нера­
венство
llq>'(x)ll ~ q, (7.8)
где О ~ q < l, q - постоянная.
Тогда независимо от выбора начального приближения х<0> из ука­
занной а-окрестности корня итерационная последовательность не
выходит из этой окрестности, метод сходится со скоростью геомет­
рической прогрессии и справедлива следующая оценка погрешности:
1/х<11> -xl/ s q11 //x<0>- xl/. • (7.9)
244

246. § 7.2. Метод простой итерации
Замечание l. Условие (7.8), грубо говоря, означает, что в
окрестности решения производные д~;fдхj для всех i и j должны
быть «достаточно малы по модулю». Иными словами, систему
(7. l) следует преобразовать к такому виду (7.5), чтобы функции ~.
слабо менялись при изменении аргументов, т.е. были <<почти
постоянными». Каких-либо общих рецептов, как это следует
делать, в общем случае нет.
Замечание 2. В условиях теоремы 7.1 верна апостериорная
оценка погрешности
l/x<11>-xl/ ~ _q_ /lx<11>-х<11 - 1 >11,
l-q
которая удобна для формулирования критерия окончания итера­
ций, если известна величина q. Однако найти значение q, удовле­
творяющее неравенству (7.8) для всех х из некоторой а-окрестно­
сти корня, далеко не просто. В ряде случаев при наличии
достаточно хорошего начального приближения х<0> можно, считая,
что q "" q0 = ll~'(x<0>)11 , использовать следующий практический
критерий окончания итерационного процесса:
11 (11) (11-I)ll < _ 1-qo
Х -Х -Ei---E.
qo
(7.10)
Пр и мер 7.4. Используя метод простой итерации,
ностью Е = 10-3 решение х 1 , х 2 системы (7.4).
найдем с точ-
Приведем систему к виду, удобному для итераций:
х1 = зj8х1х2 -х~.
v 3 Х2 XI
здесь ~ 1 (х 1 , х2) = 3 8х 1х2 -х2 , ~ix 1 , х2) = х2 + - - - .
lnx2 lnx1
Проверим выполнение условия
рис. 7.3). Вычислим матрицу Якоби
сходимости вблизи точки С (см.
'( ::: ::~1- 3(8x1x:x~x~)2/J~ XI, Х2) =
дЦ>2 дq>2 _1_ - _1_
дх 1 дх2 In2x1 ln:t1
3 213
3(8т 1 х2 -х2 )
l+-1___1_
lnx2 ln2x2
245

247. Глава 7. Методы отыскания решений систем нелинейных уравнений
Так как х 1 ""3.8 и х 2 ""2, то для х"" х ""(3.8, 2) имеем
<р'(х , х ) ""<р'(3.8, 2)"" [ 0.379 0.4361
1 2 -О 188 О 36 Jj
Тогда llqi'(x1,x2)1i 00 o:llqi'(3.8,2)11 00 ""0.379 + 0.436 =0.815.Следова­
тельно, метод простой итерации
(k+ 1) _ з /8 (k) (k) ( (k))З
XI - 't.J х 1 Х2 - Х2 ,
(k) (k)
(k+ 1) (k) Х2 ~1
Х2 =х2 +W-W
lnx2 lnx1
(7.11)
будет сходиться со скоростью геометрической прогрессии, знаменатель
которой примерно равен 0.815, если начальные приближения брать
в достаточно малой окрестности решения
Возьмем х0> = 3.8, х~0> = 2 и будем вести итерации по формулам (7.11),
используя критерий окончания (7.10), в котором Е = ю-3, q0 = 0.815.
Результаты вычислений с шестью знаками мантиссы приведены в табл. 7.1.
Таблица 7.1
k о 1 2 3 4
(k)
Х 3 80000 3 75155 3 74960 3 75892 3 76720
(k)
Х2 2 00000 2 03895 2 06347 2 07498 2 07883
Продолжение табл. 7. 1
k 5 6 7 8 9
(!)
х, 3 77198 3 77399 3 77450 3 77440 3 77418
(k)
Х2 2 07920 2 07850 2 07778 2 07732 2 07712
При k = 9 критерий окончания выполняется и можно положить
х 1 = 3 774 ±О 001, х 2 = 2.077 ± 0.001. А
3. Влияние поrрешности вычислений. В силу наличия погреш­
ностей при вычислении на компьютере получается не последователь-
ность x<k), удовлетворяющая равенству (7 7), а последовательность ;щ,
удовлетворяющая равенству
х<*+ 1) = <р*(х<*»· (7.12)
246

248. § 7.2. Метод простой итерации
Будем считать, что абсолютная погрешность вычисляемых значений
<р*(х) вектор-функции <р мала и что ll<p(x)-<p*(x)ll s;Л(<р*). Наличие
погрешности вычисления <р приводит к появлению области неопреде­
ленности решения х ,радиус & которой можно приближенно оценить,
воспользовавшись неравенством & ~ Е •= Л(<р*)!( 1- q) в том случае,
если ll<p'(x)ll :$ q.
Сформулируем следующий результат, являющийся аналогом теорем
4.5 и 6.3.
Теорема 7.2. Пусть выполнены условия теоремы 7.1 и для всех х
-
из а-окрестности решения х выполнено неравенство
-· Л(qi*)Е =--<а
1-q
ll<p(x)- <p*(x)ll :S Л(<р*). Предположим также, что
(т.е. величина Л(<р*) достаточно мала). Тогда если вычисления по
формулам (7.7) и (7.12) начинаются с одного начального приближения
х<0> = .Х<0> , принадлежащего а1-окрестности решения х (где а1 =
= mш {а, (а - Е •)/q} ), то последовательность .Х<п> не выходит за
пределы а-окрестности решения х и для всех п ~ 1 справедливы
оценки
llx<п>-.X<п>ll :$ &*,
11.X<п>-.Xll s; qnll.X<0>-xll + &*,
11.X<п>- xll :$ _q_ 11.Х<п>-.Х<п- 1>11 + &*. 8
1-q
4. Модификации метода простой итерации. В некоторых случаях
для ускорения сходимости полезно использовать следующий аналог
метода Зейделя (см. § 6.2):
(k + 1) - ( (k)
х, -<р, х, ' (k)
Х3 '
(k+I)_ ( (k+I) (k) (k)
Х2 -<р2Х1 ,Х2 • Х3 •
(k+I)_ ( (k+I) (k+I) (k)
Х3 -<р3Х1 ,Х2 ,Х3,
(k)
"" хт ),
(k)
"" хт ),
(k)
... ,Хт ),
(k + 1) - ( (k + 1) (k + 1) (k + 1) (k))
Хт -<pmxl ,Х2 ,Х3 ,""Хт.
247

249. Глава 7. Методы отыскания решений систем нелинейных уравнений
Другой вариант метода Зейделя состоит в следующем: i-я компо­
нента решения (i = 1, 2. ..., т) на (k + 1)-й итерации метода опреде­
ляется как решение нелинейного уравнения
F;(x~k + 1»= 0,
(k+l) (k+l) (k) (k)
где F;(x;) = f;(x 1 , ..., Х;_ 1 , Х;, Х;+ 1, ••• , хт ).
Преимущества этого метода1 состоят в возможности использования
методов решения уравнений с одним неизвестным и в отсутствии необ­
ходимости приведения системы уравнений к виду, удобному для ите­
раций. Указанный метод сходится, если для матрицы Якоби f (х)
выполнены условия строчного диагонального преобладания.
Иногда существенный выигрыш дает использование нелинейного
SОR-метода, являющегося аналогом метода релаксации (см. § 6.3). В
нем после вычисления очередной i-й компоненты (k + 1)-го прибли­
жения по формуле метода Зейделя
Л(k+ 1) (k + 1) (k + 1) (k) (k)
Х; =<J1;(X1 , .•.,Xi-1 ,Х; , ...,Хт)
б (k + 1)
при лижение х; вычисляют по формуле
x~k + 1) = ~~k+ 1) +(ro _ 1)( ~~k + 1) _ x~k>)
1 l J 1 '
где ro - параметр релаксации.
§ 7.3. Метод Ньютона дп• реwениt1
систем нелинейных уравнений
1. Описание метода. Обобщим метод Ньютона, изложенный в § 4.6
для решения одного нелинейного уравнения, на решение систем нели­
нейных уравнений (7.1 ). При этом будем исходить из трактовки метода
Ньютона как метода линеаризации.
Предположим, что исходя из начального приближения х<0> к
решению х построены приближения x(l), хщ, ..., х<п>. Заменим в
системе (7.1) каждую из функций!, (i = 1, 2, ..., т) главной линейной
частью ее разложения по формуле Тейлора в точке х<п);
т дf;(x<n>)
f;(x) o::f;(x<n>) + L ~ (хгх}п».
j=l 1
1 Эrот метод иногда называют нелинейным методом ЗейделR.
248

250. § 7.3. Метод Ньютона для решения систем нелинейных уравнений
В результате придем к системе линейных алгебраических уравнений
т дf1(х(п))
/ 1(x(n)) + L дх (х1 -xj"» =О,
;=1 }
т дf (x(n))
f2(x<n>) + L 2дх (х1 -xj">) =О,
;=1 }
т дf. (х(п))
fт(х<п>) + L тдх (х1 -xj">) =О,
;=1 }
имеющей в матричной форме записи следующий вид:
ftx<п>) +f'(х<п>)(х -х<п>) =О; (7.13)
здесь/'- матрица Якоби (7.3).
Предположим, что матрица f'(х<п>) невырожденная, т.е. существует
обратная матрица (f'(x<n>))-1• Тогда система (7.13) имеет единственное
решение, которое и принимается за очередное приближение х<п + 1> к
решению х. Таким образом, приближениех<n + 1>удовлетворяет равенству
flx(n)) +f'(х<п>)(х<п + 1) -x(n)) = О, (7.14)
выражая из которого х<п + 1>, выводим итерационную формулу метода
Ньютона:
(7.15)
3а меч ан и е. Формула (7.15) предполагает использование трудо­
емкой операции обращения матрицы (см. гл. 5), поэтому непосредст­
венное ее использование для вычисления х<п + l) в большинстве слу­
чаев нецелесообразно. Обычно вместо этого решают эквивалентную
системе (7.14) систему линейных алгебраических уравнений
f'(х<п>)лх<п+ 1) = -ftx<п>) (7.16)
относительно поправки Лх (п + 1>= х<п + 1>- х<п>. Затем полагают
х<п + 1) =x(n) + лх<п + 1), (7.17)
2. Сходимость метода. Сформулируем основную теорему о сходи­
мости метода Ньютона.
Теорем а 7.3. Пусть в некоторой окрестности решения х системы
(7.1) функции!, (1 = l, 2, ", т) дважды непрерывно дифференцируемы и
матрица f'(x) невырождена. Тогда найдется такая мш~ая о-окрест-
249

251. Глава 7. Методы отыскания решений систем нелинейных уравнений
ность решения х , что при произвольном выборе начш~ьного прибли­
жения х<О> из этой окрестности итерационная последовательность
метода Ньютона не выходит за пределы окрестности и справедлива
оценка:
Эта оценка означает, что метод сходится с квадратичной скоростью.
Квадратичная скорость сходимости метода Ньютона позволяет
использовать простой практический критерий окончания итераций
lx(n) _x(n- l>j < Е. (7.18)
Пример 7.S. Использовав метод Ньютона, найдем с точностью i: =
= 10-4 решение х 1, х2 системы (7.4).
Возьмем х~0> = 3.8, х~0> = 2 и будем вести вычисления по формулам
(7.16), (7.17), в которых
Результаты вычислений с шестью знаками мантиссы приведены
в табл. 7.2.
Таблица 7.2
k о 1 2 3
(k)
Х1 3.80000 3. 77258 3.77388 3.77389
(k)
Х2 2.00000 2.07189 2.07708 2.07710
При k = 3 критерий окончания итераций x<k> - x<k - 1> 00 < Е = lо- 4
выполняется и можно положить Х 1 = З.7739 ± О.ООО 1, Х 2 = 2.0771 ±
± 0.0001 .•
3. Трудности использования метода Ньютона. Изложенные в § 4.6
трудности использования метода Ньютона не только сохраняются при
применении его к решению систем нелинейных уравнений, но
и усугубляются. Во-первых, возникает проблема вычисления на каждой
итерации матрицы f'(x) из т2 частных производных, что само по себе
может оказаться весьма сложным делом. Во-вторых, обостряется про-
250

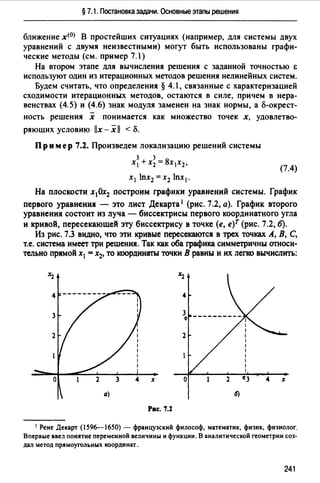
252. § 7.4. Модификации метода Ньютона
блема нахождения хорошего начального приближения. Ее решить
в многомерном случае гораздо труднее, чем в одномерном.
4. Модифицированный метод Ньютона. Модифицированный
метод Ньютона призван существенно ослабить требования к
начальному приближению. Опишем одну его итерацию.
Сначала, как и в классическом варианте метода, решают систему
f'(х<п>)лх<п + 1) = -f(x(n))
относительно вектора лх<п + 1).
Затем находят число ап, решая задачу одномерной минимизации
Fn(an) = min Fn(a); Fn(a) = llf(x(n) + аЛх(п+ 1>)11.
а
Следующее приближение вычисляют по формуле
х<п + 1) =х<п) + аплх<п + 1).
Подробнее с модифицированным методом Ньютона можно ознако­
миться в [104].
5. Влияние погрешности вычислений. Пусть f' и (/')• - вычис­
ляемые на компьютере приближенные значения вектор-функции / и
матрицы Якоби f'. Пусть для решения системы линейных алгебраических
уравнений (7.16) используется схема частичного выбора (см. § 5.5). Будем
считать, что матрицаf достаточно хорошо обусловлена (cond(/')E,.. « 1)
и вычисляется не слишком грубо ( 11/' -(/').11 « 11/'11 ). Тогда при
выборе начального приближения из малой окрестности решения метод
Ньютона является устойчивым и дает возможность найти решение с
гарантированной точностью Е <':: Е"• = ll(f'(x))-1llЛ(/").
§ 7.4. Модификации метода Ньютона
Если оценивать качество метода Ньютона только по числу необхо­
димых итераций, то следовало бы сделать вывод о том, что этот метод
стоит применять всегда, когда он сходится. На практике для достижения
разумной точности Е при выборе достаточно хорошего начального при­
ближения х<0> требуется, как правило, три-пять итераций.
Однако при оценке общей трудоемкости метода следует учитывать,
что на каждой итерации требуется выполнение следующей дополни­
тельной работы:
1) вычисление т компонент вектора f(x<n>);
2) вычисление т2 компонент матрицы Якоби f' (x<n>);
3) решение системы линейных алгебраических уравнений (7.16}.
251

253. Глава 7. Методы отыскания решений систем нелинейных уравнений
Существует большое число модификаций метода Ньютона, позво­
ляющих в тех или иных ситуациях снизить его трудоемкость либо
избежать необходимости вычисления производных. Рассмотрим кратко
некоторые из таких модификаций, с учетом того, что их одномерные
аналоги были изучены более подробно в § 4.7.
l. Упрощенный метод Ньютона. Заменим в расчетных формулах
метода Ньютона (7.16), (7.17) матрицу/' (х<п>), зависящую от п, посто­
янной матрицей А =f'(x<0)). В результате получим расчетные формулы
упрощенного метода Ньютона:
АЛх(п + ) = -J(x<n>),
х<п + ) = х<п) + Лх(п + 1).
(7.19)
(7.20)
Можно показать, что этот метод сходится со скоростью геометри­
ческой прогрессии, если начальное приближение х<0> выбрано доста­
точно близким к решению х , причем знаменатель прогрессии q тем
меньше, чем ближе х<0> к х .
По сравнению с методом Ньютона число итераций, необходимое
для достижения заданной точности Е:, существенно возрастает. Тем не
менее общие вычислительные затраты могут оказаться меньше.
Причины этого состоят в следующем. Во-первых, вычисление матрицы
Якоби производится здесь только один раз; во-вторых, как нетрудно
видеть, при использовании упрощенного метода Ньютона (7. 19), (7.20)
многократно решается система линейных уравнений с фиксированной
матрицей А и различными правыми частями. Это означает, что при
решении систем (7.19) методом Гаусса возможно применение LU-раз­
ложения матрицы А, которое резко уменьшает число операций, необхо­
димых для вычисления Лх<п + 1) (см. гл. 5).
2. Использование формул числениоrо дифференцирования.
Довольно часто вычисление производных дf;!дхj• являющихся эле­
ментами матрицы /', затруднено или вообще невозможно. В такой
ситуации для приближенного вычисления производных можно попытаться
использовать формулы численного дифференцирования (см. гл. 12).
Например, можно использовать следующую конечно-разностную аппрок­
симацию производной·
дf; (п)
- (х<п)) ::::::J.. =
дхj '1
252

254. § 7.4. Модификации метода Ньютона
Параметры hy> '#О (j = 1, 2, ..., т) - это конечно-разностные шаги.
Если в расчетных формулах метода Ньютона (7.16), (7.17) заменить
матрицу f (x(n>) аппроксимирующей ее матрицей .J(n) с элементами
l;jп> , то получим следующий итерационный метод:
J(n)дх(п + ) = -f(х<п>),
х<п + 1) =x(n) + дх<п + 1)_
(7.22)
(7.23)
В простейшем варианте этого метода шаги hj (j = 1, 2, "" т) не
зависят от п. Отметим, что выбор величины шагов представляет собой
не очень простую задачу. С одной стороны, они должны быть доста­
точно малыми, чтобы матрица .J(n) хорошо приближала матрицу
f (x<n>), с другой, они не могут быть очень малы, так как в этом случае
влияние погрешностей вычисления функций fj на погрешность
формулы (7.21) численного дифференцирования становится катастро­
фическим (выполняется вычитание близких приближенных чисел).
Следующие три метода можно рассматривать как варианты метода
(7.22), (7 23), в которых реализованы специальные подходы к вычис-
лению вектора h(n) = (h~n>, h~n>, "" h~>{. Для того чтобы приведенные
ниже рассуждения были формально корректными, в формуле (7.21)
(n) дf; (n)
положим Jij = - (x<nJ), если оказалось, что hj = О.
дхj
3. Метод ложного положения. Пусть с - фиксированный вектор.
Положим h(nJ = с - х<п>. Тогда формулы (7.21Н7.23) определяют
метод ложного положения, обладающий линейной скоростью сходи­
мости, если вектор с и начальное приближение х<0> выбраны доста­
точно близко к решению.
4. Метод секущих. В одном из наиболее популярных своих вари­
антов метод секущих можно рассматривать как метод (7.21 Н7.23),
где h(n) = х<п - IJ - x!n)_ Метод секущих является двухшаговым: для
вычисления очередного приближения х<п + 1> используют два преды­
дущих приближения х<п> и х<п - 1>. Для того чтобы начать вычисления,
необходимо задать два начальных приближения х<0> и x(I>.
При удачном выборе начальных приближений x<0J и x< 1J метод
секущих сходится со сверхлинейной скоростью с порядком сходимости
р = (J5 + 1) /2.
253

255. Глава 7. Методы отыскания решений систем нелинейных уравнений
5. Метод Стеффенсена. Вычисления по методу Стеффенсена про­
изводят по формулам (7.21Н7.23), где h(n) =f(x<n>). Замечательно то,
что хотя этот метод не требует вычисления производных и в отличие от
метода секущих является одношаговым, он, как и метод Ньютона,
обладает свойством квадратичной сходимости. Правда, как и в методе
Ньютона, его применение затруднено необходимостью выбора
хорошего начального приближения. По-видимому, для решения нели­
нейных систем вида (7.1) метод Стеффенсена чаще окажется лучшим
выбором, чем метод секущих или метод ложного положения.
Как и в одномерном случае (см. § 4.7), следует отметить, что методы
секущих и Стеффенсена теряют устойчивость вблизи решения (факти­
чески это происходит при попадании приближения х<п> в область неоп­
ределенности решения х ). Поэтому при использовании этих методов
важно вовремя прекратить выполнение итераций.
6. Метод Бройдена. Существует класс квазинъютоновских методов,
обобщающий на случай систем уравнений метод секущих. Среди этих
методов заслуженной популярностью пользуется метод Бройдена.
В этом методе наряду с последовательностью приближений .x(k) к
решению вычисляется последовательность приближений JJ(,k) к матрице
Якоби/'( х ). Пусть заданы начальные приближения .х<0> :== х и ]Jf,O) :==
:==f'(x ). Следующие приближения при k = О, , ..., вычисляются по
формулам
в<k>Лх(k + 1>= -ik> ,
x(k + 1) = x<k> + лх<k + 1>,
лik+ 1>= лх<k+ 1>)- Лхщ),
в<1:+ 1) = в<k> + 1 (Л/<k +1>_ в<k>лх<k +1>)(Лх(k+1 ))т
llлx<k + 1>ii ~
Этот метод обладает сверхлинейной сходимостью.
§ 7.5. О некоторых подходах к решению зада11
nокаnизации и отыскания
решений систем неnинейных уравнений
Подчеркнем еще раз, что одной из наиболее трудных проблем, возни­
кающих при решении систем нелинейных уравнений, является задача
локализации решения. Изложим некоторые подходы к ее решению,
широко применяемые в практике вычислений. Указанные методы можно
применять и для вычисления решения с заданной точностью Е.
254

256. § 7.5. О некоторых подходах к решению задач локализации систем нелинейных уравнений
1. Использование методов минимизации. Иногда бывает полезно
свести задачу отыскания решения системы нелинейных уравнений к
задаче отыскания минимума функции многих переменных. В про­
стейшем варианте это сведение выглядит следующим образом. Введем
т
функцию Ф(х) = L(f,(x))2 Она неотрицательна и достигает своего
1=1
минимума (равного нулю) тогда и только тогда, когда/,(х) =О для всех
1 = 1, 2, ..., т, т.е. когда х является решением системы (7.1 ).
Применив для отыскания минимума функции Ф один из итераци­
онных методов минимизации - методов спуска (см. гл. 10), можно
найти вполне удовлетворительное приближение к решению х ,которое
затем имеет смысл использовать как начальное приближение х<0> в
одном из итерационных методов решения нелинейных систем.
Выгода от указанного сведения исходной задачи к задаче миними­
зации состоит в том, что, как правило, методы спуска имеют более
широкую область сходимости. Использование методов спуска можно
рассматривать и как один из способов локализации решений системы
(7.1 ). Применение на заключительном этапе методов, специально ори­
ентированных на решение нелинейных систем, вызвано тем, что вблизи
искомого решения методы спуска сходятся медленнее.
Следует отметить, что функция Ф(х) может иметь и ненулевые
локальные минимумы, и в зависимости от выбора начального прибли­
жения методы спуска могут приводить к точкам локального минимума,
не являющимися решениями системы (7.1).
Пример 7.4. Решения системы (7.4) являются точками глобального
минимума функции
Ф(х1, х2) = (х~ + х~ - 8х1х2)2 + (х1 lпх2 -х2 lпxi)2. •
2. Метод продолжения по параметру. Сначала заметим, что
довольно часто на практике встречаются ситуации, когда система нели­
нейных уравнений естественным образом зависит от некоторого пара­
метра t, т.е. имеет вид
f(x, t) =О, (7.24)
а решение ее следует найти при некотором фиксированном значении
параметра, например при t = 1. В частности, этим свойством обладает
система из примера 7.1. Предположим, что при каждом t е [О, 1]
система (7. 24) имеет решение х = х( t), непрерывно зависящее от
255

257. Глава 7. Методы отыскания решений систем нелинейных уравнений
х(О) =:X(t0)
Рис. 7.5
параметра t, причем при t = О решение системы f(x, t) = О известно
либо легко вычисляется.
Таким образом, семейство решений x(t) описывает в пространстве
Rm траекторию, начальная точка х(О) которой известна, а конечная
х (1) подлежит определению (рис. 7.5).
И в тех случаях, когда система не зависит от параметра, можно
ввести параметр t так, чтобы были выполнены указанные выше
условия. Например, если х• - известное приближение к решению
системы /(х) =О, то можно рассмотреть систему вида (7.24), положив
/(х, 1) =/(х} - (1 - t)/{x*).
Введем на отрезке [О, 1) набор точек О= 10 < 11 < ." < tN = 1. Исполь­
зовав тот или иной итерационный метод, решим последовательно для
k =О, 1, 2, "., N системы /(х, tk) =О. При этом за начальное приближение
к x(tk) будем принимать решение x(tk- 1). Если разность tk - tk _ 1
ДОСТаТОЧНО мала, ТО МОЖНО ОЖИДаТЬ, ЧТО X(tk- 1) будет ДОСТаТОЧНО
хорошим начальным приближением к x(tk)' обеспечивающим сходи­
мость используемого итерационного метода.
256
Замечание. Довольно часто на практике проводится исследо­
вание зависимости определенных характеристик объекта от неко­
торого параметра 1. Для таких задач метод продолжения естествен.
Более того, точки t0, 11, "" IN можно выбрать, использовав допол-
нительные соображения, причем решение x(tk) представляет
интерес не только для k = N, но и для всех k = О, 1, "" N.

258. § 7.5. О некоторых подходах к решению задач локализации систем нелинейных уравнений
3. Метод дифференцирования по параметру. Предположим, что
решение x(t) системы (7.24) является гладкой функцией параметра t.
Дифференцируя тождество f(x(t), t) = О по t, получаем
t~<x<1>. 1)x'(t) +J;(x(t), t) = о.
Здесь f~(x, t) - матрица с элементами дfi/дх/х, t) (i,j = 1, 2, ..., m),
а t;(x, t) - вектор-столбец с элементами дf;!дt(х, t) (i = 1, 2, ..., m).
Таким образом, если матрица!~ невырождена (detf~ *О), ТО x(t)
является решением задачи Коши для системы обыкновенных диффе­
ренциальных уравнений
x'(t) = -[f~(x(t), t)]-1/;(x(t), t), х(О) = х(О). (7.25)
Интересующее нас значение решения х (1) можно теперь найти прибли­
женно, применяя численные методы решения задачи Коши (см. гл. 14).
Например, метод Эйлера приводит к процессу
x<k+ l) =x<k) - (tн 1 - tk) [f~(хщ, tk) ]-11;cx<k>, tk) , k = О, 1, ..., N- 1,
где х(О) = х(О), x(k) - приближение к x(tk) (рис. 7.6).
Конечно, метод Эйлера приведен здесь только для удобства иллюст­
рации, а в реальной ситуации используется один из методов более
высокого порядка точности.
:х-<о) =xUo>
Рис. 7.6
257

259. Глава 7. Методы отыскания решений систем нелинейных уравнений
Полученное указанным способом значение x!NJ можно использовать
и как хорошее начальное приближение к х( l) в одном из итераци­
онных методов решения системы (7.24).
Заме чан и е l. Иногда метод дифференцирования по пара­
метру называют методом Давиденко 1.
Замечание 2. Методы продолжения и дифференцирования по
параметру нередко позволяют успешно преодолевать непростую
проблему локализации. Однако следует отметить, что эти методы
далеко не всегда оказываются эффективными и их практическое
применение требует определенной осторожности.
§ 7.6. Допоnнитеnьные замечани1
1. Существенно более подробная и богатая информация о системах
нелинейных уравнений и методах их решения содержится в книгах [74,
40]. Рекомендуем также обратиться к учебнику [9].
2. В последнее время значительный интерес проявляется к так
называемым квазиньютоновским методам, которые получаются при
специальных аппроксимациях матрицы Якоби. Часто такая аппрокси­
мация сочетается с использованием гибридных алгоритмов подобно
тому, как это делается для решения одного нелинейного уравнения (см.
§ 4.8). Полезные обсуждения таких методов можно найти в [40].
3. Иногда подходящим для решения задачи методом оказывается
метод установления см. [9]. Чаще это бывает тогда, когда решение
системы (7.1) описывает устойчивое стационарное состояние неко­
торой физической системы.
4. Рекомендовать тот или иной метод как наиболее подходящий для
решения системы нелинейных уравнений невозможно без тщательного
анализа конкретной задачи.
1Дмитрий Федорович Давиденко (1923-1995) - российский математик.
258

260. Глава В
МЕТОДЫ РЕШЕНИЯ
ПРО&ЛЕМЫ СО&СТВЕННЫХ ЗНАЧЕНИЙ
Вычисление собственных значений (чисел) и собственных векторов -
одна из тех сложных вычислительных задач, с которой часто прихо­
дится сталкиваться исследователю, занимающемуся конструированием
или анализом больших технических систем. В электрических и механи­
ческих системах собственные числа отвечают собственным частотам
колебаний, а собственные векторы характеризуют соответствующие
формы (моды) колебаний. Знание собственных чисел позволяет анали­
зировать многие процессы, исследовать и управлять ими. Оценка кри­
тических нагрузок при расчете строительных конструкций также
основана на информации о собственных значениях и собственных век­
торах матриц.
Собственные числа и собственные векторы являются важнейшими
характеристиками, отражающими существенные стороны линейных
моделей. Поэтому, конечно, дальнейшее расширение процесса матема­
тического моделирования приведет к тому, что владение методами
решения проблемы собственных значений станет неотъемлемым эле­
ментом высшего образования.
§ 8. 1. Постановка задачи.
Некоторые вспомогательные сведения
1. Постановка задачи. В данной главе мы ограничимся рассмот­
рением методов решения проблемы собственных значений только для
квадратных матриц А порядка т с вещественными элементами а,1 (i,j =
= 1, 2, ..., т). Будем всюду под llxll понимать норму llxll2 и под (х,у)­
скалярное произведение векторов х, у (см. § 5.2).
Напомним, что число Л. называется собственным значением (собст­
венным числом) матрицы А, если существует ненулевой вектор х, удов­
летворяющий системе уравнений
Ах= Л.х (8.1)
и называемый собственным вектором матрицы А, отвечаюшим соб­
ственному значению Л.. (Собственное значение Л. и собственный
вектор х - вообше говоря, - комплексные.)
259

261. Глава 8. Методы решения проблемы собственных значений
Запишем систему (8.1) в виде
(А - Л.Е)х = О.
Эта однородная система имеет ненулевое решение х тогда и только
тогда, когда определитель матрицы системы равен нулю, т.е.
det(A - Л.Е) = О. (8.2)
Раскрытие этого уравнения приводит к так называемому характери­
стическому (или вековому) уравнению
л_т +P1л_m-I +Р2л_т- 2 + ··· +Рт-IЛ. +Рт= О, (8.3)
представляющему собой алгебраическое уравнение степени т.
Известно, что характеристическое уравнение имеет в области ком­
плексных чисел ровно т корней Л. 1 , Л.2, ... , Л.т (с учетом их кратности).
Таким образом, каждая квадратная матрица А порядка т обладает
набором из т собственных значений Л.1 , Л.2, ..., Л.т.
Если матрица А симметричная, то все ее собственные значения
являются вещественными числами. Для несимметричных матриц воз­
можно наличие комплексных собственных значений вида Л. = а + i~ с
ненулевой мнимой частью. В этом случае собственным значением обя-
зательно является и комплексно-сопряженное число Л. = а - ф.
В ряде задач механики, физики, химии, техники, биологии требуется
получение всех собственных значений некоторых матриц, а иногда
и всех собственных векторов. В такой постановке задачу называют
полной проблемой собственных значений.
Довольно часто определению подлежат не все собственные зна­
чения и собственные векторы, а лишь небольшая их часть. Например,
существенный интерес во многих приложениях представляют макси­
мальное или минимальное по модулю собственное значение или же
собственное значение, наиболее близко расположенное к заданному
значению. Такие задачи являются примерами частичных проблем соб­
ственных значений.
Может показаться, что достаточно ограничиться только рассмот­
рением методов решения полной проблемы собственных значений, так
как все остальные проблемы являются ее частными случаями. Однако
такой подход неоправдан, поскольку ориентирует на работу по полу­
чению значительного объема заведомо ненужной информации и требует
существенно большего объема вычислений, чем это необходимо в дейст­
вительности. Поэтому для решения различных частичных проблем собст­
венных значений разработан ряд специальных методов.
260

262. § 8.1. Постановка задачи. Некоторые вспомогательные сведения
Пример 8.1. Найдем собственные числа матрицы
[
2 -9 5 ]
А= 1.2 -5.3999 6 ·
1 -1 -7.5
(8.4)
Запишем характеристический многочлен
[
2 - л. -9
Р3(Л.) = det(A - Л.Е) = det 1.2 -5.3999 - л.
1 -1
= -Л.3 - 10.8999Л.2 - 26.49945')... - 21.002.
Используя один из итерационных методов решения нелинейных урав­
нений (например, метод Ньютона), определяем один из корней уравнения
Р3(Л.) =О, а именно Л. 1 ~ -7.87279. Разделив Р3(Л.) на Л. - Л.1 , имеем
Рз{Л.)
~ Р2 (Л.) = Л.2 + 3.0271 lЛ. + 2.66765.
л. + 7 87279
Решая квадратное уравнение Р2(Л.) =О, находим корни Л. 2, 3~
~ -1.51356 ± 0.613841 i.
Таким образом, матрица А имеет одно вещественное собственное
значение Л. 1 ~ -7.87279 и два комплексно-сопряженных собственных
значения Л.2, 3 ~ -1.51356 ± 0.613841 i. .А
Численные методы решения проблемы собственных значений,
использовавшиеся до конца 40-х годов ХХ в. сводились в конечном
счете к решению характеристического уравнения (8.3). Этой класси­
ческой схеме следовали и мы в примере 8.1. При реализации такого
подхода основные усилия были направлены на разработку эффек­
тивных методов быстрого вычисления коэффициентов характеристи­
ческого уравнения. Методы такого класса получили названия прямых;
к ним относятся пользовавшиеся популярностью методы Крылова1,
Данилевского, Леверье и др.
Однако указанный подход становится неудовлетворительным, если
речь идет о вычислении собственных значений матриц, имеющих
порядок т в несколько десятков (и тем более сотен), т.е. матриц
довольно скромных по современным понятиям размеров.
1 Алексей Николаевич Крылов (1863-1945) - русский математик, механик и кораб­
лестроитель, является авторо" первого в мировой научной литературе курса по числен­
ным методам - изданных в 1911 г. «Лекций о приближенных вычислениях».
261

263. Глава 8. Методы решения проблемы собственных значений
Одна из причин состоит в том. что хотя задачи (8.1) и (8.3) фор­
мально эквивалентны, они имеют разную обусловленность. Так как
корни многочлена Рт(х) высокой степени чрезвычайно чувствительны
к погрешностям в коэффициентах, то на этапе вычисления коэффици­
ентов характеристического уравнения может быть в значительной
степени потеряна информация о собственных значениях матрицы.
С появлением компьютеров широкое распространение получили
итерационные методы решения проблемы собственных значений, не
использующие вычисление характеристического многочлена. К началу
60-х годов ХХ в. эти методы практически полностью вытеснили
прямые методы из практики вычислений.
2. Преобразование подобия. Говорят, что матрицы А и В подобны,
если существует невырожденная матрица Р (матрица подобия) такая,
что В = р- 1 АР. Само преобразование матрицы А к виду В = р-1АР
называют преобразованием подобия. Преобразование подобия матрицы
возникает естественным образом как результат замены переменных
(или перехода к новому базису) в пространстве т-мерных векторов.
Действительно, пусть у - результат применения матрицы А к вектору х,
т.е. у = Ах. Произведем замену переменных х = Рх', у = Ру'. Тогда
равенство у= Ах примет виду'= Р- 1АРх'. Это означает, что в новых
переменных то же самое преобразование осуществляется уже не мат­
рицей А, а матрицей р- 1АР, подобной А.
Важно то, что и полученная в результате преобразования подобия
матрица имеет тот же набор собственных чисел. В самом деле, рас­
смотрим характеристический многочлен для матрицы Р- 1 АР и вос­
пользуемся тем, что определитель произведения квадратных матриц
равен произведению соответствующих определителей:
det(P-1AP-ЛE) = det(P-l(A -Л.Е)Р) = detP-1 det(A-Л.E) detP= det(A-ЛE).
Таким образом, характеристические многочлены, а следовательно,
и собственные числа матриц А и Р- 1АР совпадают. Соответствующие
собственные векторы х их' не совпадают, но, как нетрудно установить,
они связаны равенством х = Рх'.
Если бы матрицу А с помощью преобразования подобия или после­
довательности таких преобразований удалось привести к верхнему
треугольному виду, то проблему вычисления собственных значений
262

264. § 8.1. Постановка задачи. Некоторые вспомогательные сведения
можно было бы считать решенной. Дело в том, что у верхней тре­
угольной матрицы
Ь11 Ь12 ··· b1m]
В= ~.. -~2·2·:-.-.~~~
о о ... ьтт
(8.5)
собственными числами являются элементы главной диагонали Ь;;·
В этом нетрудно убедиться, если записать характеристический мно­
гочлен: det(B - ЛЕ) = (Ь 11 - Л.) (Ь22 - А.) ... (Ьтт - Л.).
Оказывается, что преобразованием подобия матрицу А можно при­
вести к еще более простому виду, чем (8.5). Справедлива (см. [27]) еле-
дующая теорема.
Теорем а 8.1. Любую квадратную матрицу А с помощью преобра­
зования подобия можно привести к следующему виду:
Л.1 0"1 о о ... о о
о Л.2 0"2 о о о
Р- 1АР= Л = о о Л.3 0"3 о о
(8.6)
..........................
о о о о ... Л.т- ат-
о о о о ... о л.т
Здесь Л. 1 , Л.2, ..., Лm - собственные числа матрицы А. Числа а; при­
нимают одно из двух значений О или 1, причем если а; = 1, то обяза­
тельно Л.; = Л.; + 1• 8
Матрица (8.6) называется жордановой формой матрицы А.
3. Матрицы простой структуры. В этой главе особое внимание
будет уделено матрицам простой структуры, т.е. матрицам, которые с
помощью преобразования подобия можно привести к диагональному виду:
p-•AP•D• ~".~~.:.~.]·о о ... л.т
(8.7)
263

265. Глава 8. Методы решения проблемы собственных значений
Запишем равенство (8.7) в виде АР= PD и заметим, что оно верно
тогда и только тогда, когда каждый j-й столбец матрицы Р является соб­
ственным вектором матрицы А, отвечающим собственному значению Л.j"
Таким образом, верна следующая теорема.
Теорем а 8.2. Матрица А является матрицей простой структуры
тогда и только тогда, когда она и.иеет т линейно независu.иых собст­
венных векторов е 1 , е2, •••, ет, отвечающих собственным значениям
Л.1 , Л.2, .•• , Л.т соответственно. 8
Указанные в теореме 8.2 собственные векторы е1 , е2, ... , ет,
образуют базис в пространстве т-мерных векторов. Поэтому каждый
т-мерный вектор х может быть однозначно представлен в виде
линейной комбинации этих векторов:
(8.8)
Какие же матрицы заведомо могут быть приведены к диагональному
виду? Следующие два предложения частично отвечают на этот вопрос.
Теорема 8.3. Если все собственные значения матрицы А раз­
личны, то она является матрицей простой структуры. 8
Теорема 8.4. Если А - вещественная сu.иметричная матрица,
то, она подобна диагональной матрице, причем матрица подобия Р
может быть выбрана ортогональной (т.е. удовлетворяющей условию
р-1 =рт;. 8
4. Локализация собственных значений. С помощью так назы­
ваемых теорем локализации иногда удается получить грубые оценки
расположения собственных чисел. Изложим самый известный из этих
результатов - теорему Гершгорина1•
т
Пусть r; = L /a;j / - сумма модулей внедиагональных элементов
j=I
j";
1-й строки матрицы А. Обозначим через S; замкнутый круг радиуса r; на
комплексной плоскости с центром в точке а;;. т.е. S; = {z Е С: /z - a;;I ~
~ r;}. Будем называть круги S; кругами Гершгорина. Имеет место сле­
дующее утверждение.
1 Семен Аронович Гершrорин (1901-1933) - российский математик. Результат,
о котором идет речь, был опубликован им в 1931 г.
264

266. § 8.1. Постановка задачи. Некоторые вспомогательные сведения
Теорема 8.5. (теорема Гершгорина). Все собственные значения
матрицы А лежат в объединении кругов S1, S2, ••• , Sm.
До к аз ат ель ст в о. Возьмем произвольное собственное значение А.
матрицы А и соответствующий собственный вектор х. Пусть х, - мак­
симальная по модулю координата вектора х. Запишем i-e уравнение
системы (8.l) в следующем виде:
(а11 - А.)х, = -,LalJxJ.
} ~·
Из этого равенства с учетом оценки 1х/ х, 1 ~ l следует неравенство
1а11 - А.1 ~ L 1alJ11:1~ r,.
} ~· 1
Таким образом, А. Е S1• 8
Пр и мер 8.2. Для матрицы
А= [=~.50.8
0.5 0.5~
-3.5 1.5
-0.5 0.5
круги Гершгорина изображены на рис. 8.1. Здесь r 1 = l, r2 =2, r3 = 1.3. .А.
Рис. 8.1
Следующий результат является полезным дополнением к теореме
Гершгорина.
Теорем а 8.6. Если k кругов Гершгорина образуют замкнутую
область G, изолированную от других кругов, то в области G находится
ровно k собственных значений матрицы А (с учетом их кратности).
Следствие. Если какой-либо круг Гершгорина изолирован, то он
содержит ровно одно собственное значение матрицы А. •
265

267. Глава 8. Методы решения проблемы собственных значений
Пр им ер 8.3. Для матрицы А из примера 8.2 в объединении кругов
S1 и S2 находится ровно два собственных значения Л.1 и Л.2, а круг S3
содержит ровно одно собственное значение Л.3. .&
S. Отношение Рэлея. При вычислении собственных чисел и собст­
венных векторов симметричных матриц важную роль играет функция
( ) - (Ах,х) (8.9)
рх - -(-),
х,х
называемая отношением Рэлея 1• Следующее предложение частично
объясняет значение этой величины.
Теорема 8.7. Пусть А - симметричная матрица. Тогда спра­
ведливы следующие утверждения:
1) минимальное и максимальное собственные значения матрицы А
вычисляются по формулам
Л.min = min р(х) , Л.mах = max р(х) ;
х"о х"о
2) вектор х является стационарной точкой функции р(х) (т.е.
удовлетворяет условию grad р(х) =О) тогда и только тогда когда х -
собственный вектор матрицы А. 8
При построении методов решения проблемы собственных значений
существенно используется то обстоятельство, что если х - хорошее
приближение к собственному вектору е1, то р(х) - хорошее прибли-
жение к собственному числу Л.j.
6. Обусловленность задачи вычисления собственных значений
и собственных векторов. Пусть А. - матрица с приближенно
заданными элементами ай ~ aij. Обозначим через Л.j (j = 1, 2, "" т) соб­
ственные числа матрицы А. . Рассмотрение вопроса о том, как влияет
погрешность задания матрицы на погрешность искомых собственных
значений, начнем с формулировки следующего известного результата.
Теорем а 8.8. Пусть А и А. - симметричные матрицы, а Л.j и л.j• -
их собственные числа, упорядоченные по возрастанию Тогда спра­
ведливы оценки погрешности
max 1Л.j - Л.j 1 ~ llA -А .11 2 , (8.1 О)
1:SJ:Sm
(f(Л.j-Л.j)2) 112
~ llA -A.llE. 8 (8.11)
1=1
!Джон Уильям Рэлей( 1842-1919) - английский физик и математик.
266

268. § 8.1. Постановка задачи. Некоторые вспомогательные сведения
Теорема 8.8 означает, что задача вычисления собственных значений
симметричных матриц очень хорошо обусловлена. Следовательно,
в этом случае собственные числа надежно определяются заданием эле­
ментов матрицы. К сожалению, для несимметричных матриц дело
обстоит совсем иначе. Хотя задача вычисления собственных значений
и в этом случае является устойчивой, для многих несимметричных
матриц собственные значения чрезвычайно чувствительны к погреш­
ностям задания коэффициентов.
Пр им ер 8.4. Приведем принадлежащий Дж.Х. Уилкинсону [102]
пример матрицы, очень плохо обусловленной по отношению к про­
блеме собственных значений.
Собственными числами верхней треугольной матрицы 20-го порядка
20 20 о о о о
о 19 20 о о о
А=
о о 18 20 о о
....................
о о о о ". 2 20
о о о о ... о 1
являются числа А. 1 = 1, А.2 = 2, Л.20 = 20. Заметим, что для этой
матрицы характеристический многочлен Р20 (А.) = (20 - А.)(19 - А.) ".
". ( - А.) совпадает с многочленом, рассмотренным в примере 3.8 в связи
с плохой обусловленностью его корней. Добавим малое Е к элементу
а20, 1= О. В результате характеристическое уравнение примет вид
(20 - Л.)(19 - А.)".( -А.)= 2О1 9Е.
При Е = 10-10 собственные значения возмущенной матрицы таковы:
А.~"" 0.996, л.; ""2.11, л.; ""2.57, л.; 5 ""3 97 ± .09i, л.; 7 ""5.89 ± l.95i,. .
л;, 9 ""8.12 ± 2.531, Л.~0• 11 "" 10.5 ± 2.731, Л.~2• 13 "" 12.9 ± 2.531, Л.~4• 15 ""
"" 15.1 ± 1.951, Л.~6• 17 "" 17.0 ± 1.091, Л.~8 "" 18.4, Л.~9 "" 18.9, л.;0 "" 20.0.
Как нетрудно видеть, большинство значений оказались полностью
искаженными. .&
Отметим, что число обусловленности cond(A) не характеризует обу­
словленность матрицы А по отношению к проблеме собственных зна­
чений. Оказывается, что такой характеристикой чувствительности соб­
ственных значений относительно погрешности задания матрицы для
267

269. Глава 8. Методы решения проблемы собственных значений
маrрицы простой структуры служит число обусловленности матрицы Р,
столбцы которой являются собственными векторами матрицы А. В под­
тверждение сказанного приведем следующий результат.
Теорем а 8.9. Пусть Р- 1АР = D, где D - диагональная матрица из
собственных значений матрицы А. Тогда каждое собственное зна­
чение матрицы А. удалено от некоторого собственного значения
матрицы А не более чем на d = cond2(Р) llA - А. 112 . 8
Пусть х - собственный вектор матрицы А, отвечающий собст­
венному значению /..., а х• - собственный вектор приближенно
заданной матрицы А., отвечающий собственному значению Л.•.
Прежде чем обсуждать обусловленность задачи вычисления собст­
венного вектора х, заметим, что здесь вопрос о выборе меры близости
векторов х• их не является тривиальным. Выбор в качестве такой меры
величины llx-x•ll неудачен. Дело в том, что собственные векторы х• и
х не определяются однозначно. Во всяком случае после умножения
каждого из них на любые числа а 1 * О и а2 * О полученные векторы
а 1х• и а2х снова являются собственными. Поэтому имеет смысл стре­
миться не к тому, чтобы векторы х• их были близки по норме, а к тому,
чтобы они были близки по направлению. Исходя из этого, примем в
качестве меры близости х• к х величину 1sin <р 1. где <р - угол между
векторами х• и х, вычисляемый по формуле
( (х"х) )
<р = arccos llx•ll2 llxll2 •
Задача вычисления собственных векторов симметричной матрицы
хорошо обусловлена, если собственные значения хорошо отделены друг
от друга. В подтверждение сказанного приведем следующий результат.
Теорема 8.10. Пусть А и А. - симметричные матрицы. Тогда
верна оценка
llA -А.11 2
1sin <pl ~ ·у
Здесь <р - угол между векторами х• их, а у - расстояние от Л.• до бли­
жайшего из несовпадающих с Л. собственных значений матрицы А. 8
268

270. § 8.2. Степенной метод
В случае, когда матрица А несимметрична, собственные векторы
могут оказаться очень плохо обусловленными.
Замечание. Подавляющее большинство встречающихся на
практике матриц являются матрицами простой структуры. Это
обстоятельство, а также большая простота анализа методов вычис­
лений и формулировок соответствующих результатов позволяют
нам в основном остановиться на проблеме собственных значений
для матриц простой структуры.
§ 8.2. Степенной метод
Пусть требуется вычислить максимальное по модулю собственное
значение Л. 1 матрицы А, причем известно, что
(8.12)
Замечание. Собственное значение Л. 1 в данном случае должно
быть вещественным, поскольку в противном случае собственным
значением было бы также равное ему по модулю число ~1 .
1. Степенной метод без сдвигов. Опишем простейший вариант сте­
пенного метода, применяемого для вычисления Л.1 . Возьмем произ-
вольный начальный векторх<0> *О и построим последовательности век-
оо (~ 00
торов {xlk>}k=O и приближений {Л. 1 }k=I к Л.1 , использовав формулы
x<k> =Ax(k- 1),
(k) _ (xlk), x<k- 1>)
Л.1 -( (k-1) (k-1))'х ,х
(8.13)
(8.14)
Замечание. Правая часть формулы (8.14)- это просто отно­
шение Рэлея, вычисленное при х = xlk - 1>. В самом деле, Л.~k) =
= (Axlk - 1>, xlk - 1))/(x<k - 1>, x<k - 1)) = p(xlk - 1>).
Справедлива следующая теорема.
Теорема 8.11. Пусть А - матрица простой структуры, для которой
выполнено условие (8.12). Предположим, что в разложении
т
x<OJ = с1е1 + с2е2 + ." + стет = Lc,e,
1=1
(8.15)
269

271. Глава 8. Методы решения проблемы собственных значений
по нормированному базису из собственных векторов коэффициент с 1 не
равен нулю. Тогда Л~k) ~ Л1 при k ~ оо и при всех k ~ k0(~0>) верна
оценка относительной погрешности
т
где С0 = 4:Lla;I, а а;= с;/с1 , 2 :S i :S т.
i=2
(8.16)
До к аз ат ель ст в о. Как нетрудно видеть, вектор x<k> удовлетворяет
равенству x<k) = Akx<0>, т.е. получается из х<0> умножением на k-ю
степень матрицы А (отсюда и название метода). Так как Ае; = Л;е;. то
Ak е; = л;е; и из (8.15) следует
т
x<k> = Л~с1е1 + LЛ.~с1е1 . (8.17)
i=2
Положимµ;= Л;/А. 1 , 2 :S 1 :S т и
(8.18)
Заметим, что
т
:z(k) _:z<k-1)= L(µ;- l)µ~-la;e;. (8.19)
i=2
Так как 1µ; :S 1µ2 < l для всех 2 :S i :S т, а базис нормированный
(т.е. 11 e;ll2= 1 для всех i), то из (8.18), (8.19) следует, что
i=2 i=2
т т
ll:z(k) -:z(k-l)ll2 :S 21µ2'*- 1:Lla;llle;ll2 =2lµ2'*- 1:Lla;I = ICo/µ2lk-l ·
i=2 i=2
270

272. §8.2. Степенной метод
k0 -1
Выберем k0 = k0(x<0>) таким, чтобы Jµ2J С0 $ 2. Тогда для всех
k ~ k0 в силу неравенства (8.20) будет справедливо неравенство
lz<k-l>1 2 ~ 1/2. Осталось заметить, что
(При выводе этой оценки мы воспользовались неравенством Коши­
Буняковскоrо l(x, y)I $ llxll2llyll2 для х = z(k) - z<k- 1> и у= z<k- 1>.) •
Замечание 1. Если выполнены условия теоремы 18.11 и мат­
рица А симметрична, то оценка (8.16) верна уже при всех k ~ 1
спостоянной С0 = J~la~' .
Замечание 2. При выполнении условия (8.12) оценка (8.16)
(с другой постоянной С0) верна и для произвольной матрицы, а не
только для матрицы простой структуры.
Замечание 3. Если !Л 11 > 1, то lx(k)ll2 ~ оо при k~ оо (см.
формулу (8.17) и при вычислении на компьтере возможно перепол-
нение. Если же 1Л 11 < 1, то x<k>ll2 ~О и возможно исчезновение
порядка. Для предупреждения этих ситуаций обычно вектор x(k)
нормируют так, чтобы lx(k)ll2 = 1 для всех k ~ 1. Одна из исполь­
зуемых модификаций такова:
y<k> = Ax<k - 1)' л_<k> = (y<k>' x<k - 1>), x<k> = 11:~k>~l2 . (8.21)
Предполагается, что llx<0>11 2 = 1.
Теорема 8.11 для метода (8.21) остается справедливой. Более
того, последовательность x<k> сходится к собственному вектору по
направлению, т.е. sш <p<k> -+ О при k -+ оо, где <p(k) - угол между
векторамих<k) и е 1 •
271

273. Глава 8. Методы решения проблемы собственных значений
Замечание 4. Крайне маловероятно, чтобы в разложении
(8.15) векторах<О) по собственным векторам коэффициент с 1 при е1
оказался равным нулю. Теоретически в этой исключительной си­
туации метод не должен давать сходящуюся к Л. 1 последователь-
ность. Однако при вычислении на компьютере по формулам (8.12)
через несколько итераций вследствие погрешностей округления
почти наверняка появится ненулевой коэффициент при е 1 в разло-
жении вектора x(k)_ Итерационный процесс снова окажется сходя­
щимся (правда, потребуется выполнить большее число итераций).
2. Апостериорная оценка погрешности. В общем случае для
решения проблемы собственных значений не существует эффективных
апостериорных оценок погрешности, в особенности для собственных век­
торов. Более простой эта проблема выглядит для симметричных матриц.
Для оценки погрешности приближения А.• к собственному значению
А. симметричной матрицы полезно использовать следующую теорему.
Теорема 8.12. Пусть л.• - произвольное число, ах• - произ­
вольный ненулевой вектор. Тогда для любой симметричной матрицы А
существует собственное значение этой матрицы А. такое, что спра­
ведлива оценка
1
•
1
liAx• - Л•х• 112
А.- А. s; llx.112 . 8 (8.22)
Если х• - приближенно вычисленный собственный вектор, то нера­
венство (8.22) позволяет дать простую апостериорную оценку погреш­
ности вычисленного собственного значения А.•. В частности, для сте­
пенного метода (8.13), (8.14) из (8.22) следует такая апостериорная
оценка:
llx<k) - Л(k)x(k- I Jll
l л. л_(k)I < 1 2
1- 1 - llx<k-1)112
(напомним, что здесь предполагается симметричность матрицы А).
Пусть х• - ненулевой вектор, рассматриваемый как приближение
к собственному вектору х, который отвечает собственному значению А..
Далее, пусть р• = р(х*) - отношение Рэлея, r =Ах* - р*х* - вектор
llrll2
невязки, а= llx•ll 2. Если собственное значение А. хорошо отделено от
остальных собственных значений матрицы А, то для оценки погреш­
ности может быть использован следующий результат.
272

274. § 8.2. Степенной метод
Теорема 8.13. Пусть А. - ближайшее кр• собственное значение
матрицы А, х - соответствующий собственный вектор и q> - угол
между векторами х• и х. Тогда справедливы оценки
/sшq>/ ~~.у
cr2
/А.-р*/ ~-.
у
Здесь у = min /А., - р*/ - расстояние от р• до ближайшего из
А.,о<А.
отличных от А. собственных значений матрицы А. •
Приведем еще одно важное свойство симметричных матриц.
Теорема 8.14. Пусть А - симметричная матрица, х· - произ­
вольный ненулевой вектор, р* = р(х*). Тогда р• их• являются точными
собственным числом и собственным вектором некоторой симмет­
ричной матрицы А., для которой
llA -А.11 2 = cr. • (8.23)
Оценка (8.23) может оказаться очень полезной для обратного
анализа ошибок (о существе такого подхода к анализу ошибок мы
говорили в§ 3.6). Например, очень часто матрица А, для которой на
компьютере производится вычисление собственных значений,
является лишь приближенным представлением «истинной» матрицы
А , собственными значениями и векторами которой в действитель­
ности и интересуется исследователь. Пусть известен порядок погреш-
ности & = llA -All2 приближенно заданной матрицы и для найденной
• • • llAx* - p*x*ll2 ~
пары х , р = р(х ) величина cr = llx*ll2 оказывается сравнимои
с величиной Е или даже существенно меньше ее. В такой ситуации р*
и х· оказываются собственными значением и вектором матрицы А.,
которая отличается от «истинной» матрицы А почти так же, как отли­
чается от нее матрица А. Вряд ли тогда следует стремиться к полу­
чению «более точных» решений.
Пр им ер 8.5. Используя степенной метод, найдем для матрицы
(8.4) максимальное по модулю собственное значение А.1 , а также отве-
чающий ему собственный вектор.
Возьмем х<О> = ( 1, О, О)Т и будем вести вычисления по формулам (8.21 ).
273

275. Глава 8. Методы решения проблемы собственных значений
Первая итерация. Вычисляем
у1>=2х0> - 9х~0> + 5х~0> =2,
А')= 1.2х0> - 5.3999х~0> + 6х~0 > =1.2,
( 1) (0) (О)+ 7 5 (0) l
Уз =х, -х2 . Х3 = .
Тогда
л_(I) = (y(I) х(О)) =y(l(O) +y(l)x(O) +y(l(O) = 2. 1 + 1 2. о+ 1. о= 21 , 1 1 2 2 з з . .
Далее
(1)- y(I) Т
х - lly()112:::; (0.788110, 0.472866, 0.394055) .
Результаты десяти первых итераций с шестью знаками мантиссы
приведены в табл. 8.1.
Таблица 8.1
Номер итерации k ,у) щ (k) щ
1 Х1 Х1 Х3
о - 1.000000 0.000000 0.000000
1 2.00000 0.788110 0.472866 0.394055
2 -1.24159 -0.250056 0.266743 -0.930763
3 -{).08121 -0.611733 -0.593143 0.523415
4 -9.50971 0.700557 0.583736 -0.410455
5 -8.23499 -0.716752 -0.579514 0.387853
6 -7.94591 0.720030 0.578443 -0.383353
7 -7.88567 -0.720635 -0.578216 0.382446
8 -7.87462 0.720729 0.578174 -0.382446
9 -7.87294 -0.720739 -0.578167 0.382437
10 -7.87277 -0.720739 0.578167 -0.382437
Хотя мы не имеем в данном случае обоснованного критерия окончания,
по-видимому, при k = 1О следует прекратить вычисления и, округлив
результаты, положить Л. 1 :::; -7.873, е 1 "'(-0.7207, 0.5782, -0.3824)r.A.
Важными достоинствами степенного метода являются его простота,
возможность эффективного использования разреженности матрицы и
отсутствие необходимости преобразования матрицы А.
Недостаток метода в применении к многим прикладным задачам -
довольно медленная сходимость. Часто в приложениях значение 1Л.2
274

276. § 8.3. Метод обратных итераций
оказывается близким к 1Л. 1 /. Так как скорость сходимости степенного
метода определяется величиной 1~ ::::: 1, то в этом случае сходимость
будет очень медленной.
3. Степенной метод со сдвнrамн. Существует несколько способов
преодоления указанной трудности. Один из них заключается в приме-
нении степенного метода не к матрице А, а к матрице А =А - аЕ, где
а - некоторое число. Собственными значениями матрицы А являются
числа Л; - cr, получаемые сдвигом собственных значений Л; на число cr.
Если число Л. 1 - cr по-прежнему остается максимальным по модулю, то
следует попытаться подобрать cr так, чтобы сделать величину
max 1 л, - cr 1 минимальной. Если, например все собственные значения
2sisn Л. 1 -cr
положительны, то такой минимум достигается при cr = (Л.2 + Л.т)/2.
После того как приближение Л~ к первому собственному значению
вычислено, степенной метод можно использовать для вычисления оче­
редного собственного значения. Один из приемов такого использования
состоит в сдвиге собственных значений на cr = Л~. В этом случае число
Л. 1 - Л~ станет минимальным по модулю, а максимальным по модулю
окажется сдвиг другого собственного значения.
Существует несколько способов избавления от уже вычисленных
собственных чисел и соответствующих собственных векторов с целью
избежать их повторного вычисления. Эти способы принято называть
исчерпыванием. Более подробную информацию о них можно найти,
например в [23, 75).
§ 8.3. Метод обратных итераций
1. Вычисление собственных векторов методом обратных ите­
раций. Многие из методов решения проблем собственных значений
лучше приспособлены для вычисления собственных значений, чем соб­
ственных векторов. Поэтому целесообразно рассмотреть задачу вычис­
ления собственного вектора ej при условии, что уже найдено доста-
точно точное приближение Л/ к собственному значению Лj.
275

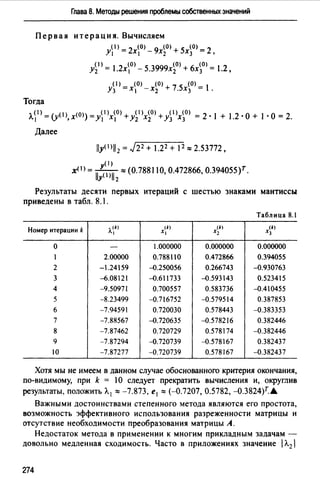
277. Глава 8. Методы решения проблемы собственных значений
Если исходить непосредственно из определения собственного
вектора, то ej следует искать как нетривиальное решение однородной
системы уравнений
(8.24)
с вырожденной матрицей А - Л.jЕ. Однако Л.j известно лишь прибли­
женно и в действительности при таком подходе вместо системы (8.24)
придется решать систему
(А -Л.}Е)х =О. (8.25)
Так как матрица А - Л.}Е заведомо невырождена, то решением системы
(8.25) является только х = О. Следовательно, непосредственное чис­
ленное решение системы (8.25) не дает возможность вычислить собст­
венный вектор.
Одним из эффективных методов вычисления собственных векторов
является метод обратных итераций. В этом методе приближения
к собственному вектору определяют последовательным решением
систем уравнений
(А - А]Е) y<k+ 1> = x<k>
с последующей нормировкой решения:
(k + 1)
x(k+ I) =~У___
i1y<k+1ъ.
(8.26)
(8.27)
В качестве начального приближения берут ненулевой вектор х<0>
с произвольно выбираемыми или даже случайными компонентами.
Часто удовлетворительным является выбор х<0> = ( l, l, .", l)r.
Чтобы понять механизм действия метода, рассмотрим случай, когда
А - матрица простой структуры, а- простое собственное значение.
Представим векторы х<0> и у< 1 > в виде линейных комбинаций собст-
т
х<0 > = "'с- е·~ 1 ,,
i=l
т
т
у< 1 >=}2а;е;.
i= 1
Так как (A-A.JE)y< 1>= }2а;(Л.;-А.j)е;, то систему уравнений (8.26)
i=I
при k = О можно записать в виде
т т
"' а· (Л.· - Л. ~ )е ·= "'с· е ·"-4 l 1 } 1 ~, ,.
i=I i=I
276

278. § 8.3. Метод обратных итераций
с;
Приравнивая коэффициенты при е;, nолучаем а;= - -•. Следова­
л;-
тельно,
m С; ! [ m
у(!)=°"' - - е.= - - с-е·+""'
~ • 1 ' , . } } ~
i=I Л;-Лj ""j-""j i=I
;"j
Л·- Л~ ]} 1
--. с;е·.
Л.;- A.j 1
(8.28)
Если p"j - Л.J 1 « р",- - ЛJ 1 для всех i * }, то второе слагаемое
в nравой части формулы (8.28) мало по сравнению с первым.
с
Поэтому у<1 >::::: - 1-. ej и вектору(!) оказывается близким по направ­
Лj-Лj
лению к собственному вектору ej"
Можно показать, что вектор x<k>, вычисляемый на k-й итерации,
имеет вид
[
т (Л· _Л.~)k ]x<k) = A(k) с-е· + °"' _1__1 с-е.
,... J J ~ А· - А.~ ' ' ,
i= 1 1 1
;"}
где 1~(k)1 --+ /cj11 при k --+ оо. Вектор x<k) сходится к ej по направ­
лению со скоростью геометрической прогрессии, знаменатель которой
IЛ· -л~I
q=max 1 1 .
;"j /Л;-Л]/
Если абсолютная погрешность значения л.j• много меньше рас­
стояния от Л.j до ближайшего из остальных собственных чисел (что экви­
валентно выполнению условия 1Л.j - ЛJ 1 « 1Л.; - ЛJ 1 для всех i *}),
то метод обратных итераций сходится очень быстро. Чаще всего доста­
точно сделать 1-3 итерации.
Пример 8.6. Использовав метод обратных итераций, найдем на
6-разрядном десятичном компьютере собственный вектор матрицы
(8.4), отвечающий собственному значению Л. 1 ::::: Л.~ = -7.8728.
Возьмем x<0J = (1, 1, 1)r. Тогда система (8.26) при k = О примет вид
9.8728yl - 9у2 + 5у3 = 1,
1.2у 1 + 2.4729у2 + 6у3 = 1,
У1 - У2 + 0.3728у3 = 1.
2П

279. Глава 8. Методы решения проблемы собственных значений
Вычисляя ее решение методом Гаусса, получаем у~1 ) = -123909,
А1 > = 99398.3, А1 > = 65749. После нормировки имеем х 1 > = -0.720736,
xi1> = -0.578166, x~I) = 0.382440.
Подставляя в правую часть системы (8.26) векrор х< 1 > и вычисляя
решеРие, находим у2> = -59671.5, А2 ) = -47867.7, А2 ) = 31663.1. Полу-
ченные после нормировки значения х2 > = -0.720737, х~2) = -0.578166,
х~2 ) = 0.382440 с машинной точностью совпадают со значениями, полу­
ченными на первой итерации. Итерации следует прервать и считать
результатом вектор е1 :::: (-0.720737, -0.578166, О.382440)т. А.
Замечание .Так как л.; почти совпадает со значением Л.1,
при котором det(A -А.1 Е) =О, то матрица А - л.;Е очень плохо обу­
словлена. Возникает естественное опасение, что большие погреш­
ности, неизбежные при реализации вычислительного процесса
(8.26), (8.27) на компьютере, могут существенно повлиять на свой­
ства приближений. К счастью, это не так; погрешность, возникаю­
щая при численном решении системы (8.26) (которая может быть
сравнима по величине cy<k>), оказывается почти пропорциональной
вектору е1. В данном случае плохая обусловленность системы не
ухудшает, а улучшает ситуацию.
В справедливости сказанного легко убедиться, если повторить
вычисления из примера 8.5, использовав калькулятор. Получен­
ные значенияу(I> иу<2 > наверняка будут иметь мало общего сука­
занными в примере. Тем не менее приближения x(I) и x<2J практи­
чески совпадут с вычисленными выше, отличаясь, возможно,
только знаком.
Замечание 2. Записывая равенство (8.26) в виде y<k + I) =
= (А - л.;Е)- 1 x<k>, замечаем, что метод обратных итераций - это
просто степенной метод, примененный к матрице (А - л.;Е)- 1 •
2. Метод обратных итераций с использованием отношения
Рэлея. Одной из проблем применения метода обратных итераций
является необходимость получения хорошего приближения к собст­
венному значению. Когда А - симметричная матрица, можно попы-
278

280. § 8.4. QR-алгоритм
таться использовать для оценки Л.1 отношение Рэлея. Этот подход при­
водит к следующему комбинированному методу:
л.<А + 1) = p(x<k>) = (Ax<k>, x(k>), k ~О;
(А_ Л.<k + IJE)y(k+ 1) =x<AJ;
(k + 1)
(k+ 1) = у
х -lly-(k_+_l_)l-12.
Предполагается, что вектор x(OJ нормирован, т.е. llx<0>il = 1.
(8.29)
(8.30)
{8.31)
Если начальное приближение х<0> хорошо аппроксимирует по
направлению вектор е1, то метод (8.29Н8.31) сходится очень быстро.
Например, если Л.1 - простое собственное значение, то сходимость
оказывается кубической. Одним из способов получения удовлетвори­
тельного начального приближения является выполнение нескольких
итераций степенного метода.
Замечание. В случае, когда метод (8.29Н8.31) сходится, он
позволяет одновременно эффективно вычислять и собственное
значение Л.1 , и соответствующий собственный вектор eJ'
§ 8.4. QR-апrоритм
В настоящее время лучшим методом вычисления всех собственных
значений квадратных заполненных матриц общего вида (умеренного
порядка) является QR-алrоритм 1.
1. Основной QR-алrорнтм. Опишем итерационную процедуру,
являющуюся основой алгоритма. Она существенно использует воз­
можность разложения произвольной матрицы в произведение ортого­
нальной и верхней треугольной матриц, т.е. так называемое QR-разло­
жение (см.§ 5.10).
На 1-й итерации с помощью метода отражений или метода вра­
щений вычисляют QR-разложение матрицы А (О) =А, имеющее вид
А (О) = Q1R1. (8.32)
Затем строят матрицу АО> = R 1Q1. Заметим, что из равенства (8.32)
следует, что R1 = Q~ 1 A(O) и поэтому A(I) = Q~1 A(OJQ1 . Таким образом.
матрицыА< 1 J иА(О) подобны (см.§ 8.1) и поэтому имеют общий набор
собственных значений Л. 1 , Л. 2, ... , Лт.
1 Этот метод независимо был предложен в 1960 г. в России lатематиком В. Н. Кубла­
новсmй и в 1961 г. в Англии системным программистом Дж. Фрэнсисом.
279

281. Глава 8. Методы решения проблемы собственных значений
На 2-й итерации находят QR-разложение матрицы лоJ, имеющее вид
л< 1 J = Q2R2, и вычисляют матрицу л<2J = R2Q2, подобную матрицеА< 1 J.
На (k + 1)-й итерации вычисляют разложение А (k) = Qk + 1Rk + 1
и строят матрицу А (k + 1) = Rk + 1Qk+ 1. Неограниченное продолжение
этого процесса дает последовательность матриц лО>, л12>, ..., л<п>, ...,
подобных матрице А.
Обратим внимание на то, что обычной поэлементной сходимости
или сходимости по норме QR-алгоритм не гарантирует. Сходимость
QR-алгоритма - это сходимость по форме последовательности при­
ближений А (п) к некоторой верхней треугольной или к верхней блочно-
треугольной матрице А , имеющей те же собственные значения, что
и матрица А. Сходимость по форме характеризуется сходимостью к
нулю поддиагональных элементов или элементов поддиагональных
блоков, тогда как наддиагональные элементы от итерации к итерации
могут существенно меняться.
Практически всегда QR-алгоритм сходится. К сожалению, в общем
случае, когда собственные значения матрицы А могут быть кратными
или комплексными, теория его сходимости весьма сложна для изло­
жения. Поэтому ограничимся формулировкой лишь одного из наиболее
известных условий сходимости - критерия Уилкинсона. Согласно
этому критерию предполагается выполнение следующих двух условий:
1) матрица А имеет простую структуру, причем модули всех собст­
венных значений различны:
IJ-1 I > Р-21 > ··· > IЛml;
2) приведение матрицы А к диагональному виду (8.7) осуществ­
ляется с помощью матрицы подобия Р, у которой все ведущие главныо
миноры ОТЛИЧНЫ ОТ нуля.
При выполнении этих двух условий последовательность А (п) схо-
дится по форме к верхней треугольной матрице А вида
Л1 х х х
о Л2 х х
А= о о Лз х
(8.33)
..............
о о о ... л.т
Здесь крестиками помечены элементы, в общем случае не равные нулю.
280

282. § 8.4. QR-алrоритм
Известно, что в рассматриваемом случае элементы а~:) матриц А <k>,
стоящие ниже главной диагонали, сходятся к нулю со скоростью гео­
метрической прогрессии, причем
la~:>1~С1 ~'k, i > j, (8.34)
т.е. скорость сходимости а::> к нулю определяете• значением отно­
шения Л, к Л.1 (заметим, что ~ < 1 при i > j).
Если условие 2) не выполнено, то сходимость по-прежнему имеет
место, но собственные значения в матрице А уже не будут распо­
ложены в порядке убывания модулей.
В общем случае предельная матрица А - блочно-треугольная (или
получающаяся из блочно-треугольной симметричной перестановкой
строк и столбцов). Наличие комплексно-сопряженных пар Лk, Ak соб­
ственных значений у вещественной матрицы А не является препят­
ствием для применения QR-алгоритма. Каждой такой паре в пре­
дельной матрице будет отвечать некоторый диагональный блок -
квадратная подматрица порядка 2, собственные числа которой сов-
падают с Л.k, Ak.
2. Ускорение QR-алrоритма. Приведенный выше вариант QR-алго­
ритма очень неэффективен по двум основным причинам. Первая из них
состоит в том, что для реализации только лишь одной итерации этого
метода требуется выполнить порядка т3 арифметических операций,
если А - матрица общего вида. Вторая причина заключается в том, что
при наличии двух близких собственных значений Л, ::::: Л, _ 1 метод схо-
дится очень медленно, так как, например элемент a~.k!_1 сходится к
нулю со скоростью геометрической прогрессии, знаменатель которой
q = ..!::...1 ""'1.
л., -1
Для того чтобы уменьшить число арифметических операций,
матрицу А предварительно с помощью подобных преобразований отра­
жения или вращения приводят к так называемой форме Хессенберга 1:
1 Герхард Хессенберг (1874-1925) - немецкий мате"атик.
281

283. Глава 8. Методы решения проблемы собственных значений
h11 h12 ··· h1.т- hlm
h2 hz2 h2,m- h2m
Н= о hз2 hз.т-1 hзт (8.35)
о о ··· hт.т- hmm
Матрица Н, в которой равны нулю все элементы hij, такие, что i >j + 1
(т.е. все элементы, расположенные ниже диагонали, непосредственно
примыкающей снизу к главной диагонали), называется матрицей Хес­
сенберга. Существуют эффективные стандартные процедуры преобра­
зования матрицы А к виду (8.35), поэтому мы не будем останавливаться
подробно на этом преобразовании. Для дальнейшего важно то, что
матрицы А и Н подобны и обладают общим набором собственных зна­
чений, а матрица подобия Р, для которой выполняется равенство
Н= Р-1АР, (8.36)
ортогональна.
После преобразования матрицы А к виду (8.35) к матрице Н при­
меняют QR-алгоритм. Эффективность такого подхода обусловлена
наличием следующих двух замечательных свойств матриц Хессен­
берга.
1°. Матрицы H(k>, порождаемые QR-алгоритмом из матрицы
Н(О) = Н, сами являются л1атрицами Хессенберга, т.е. для них hiJ> =О
при i > j + 1.
2°. Для выполнения одной итерации QR-алгоритма для матрицы
Хессенберга требуется число арифметических операций, пропорцио­
нальное т 2 •
Однако, как уже было отмечено, даже достигнутая благодаря предва­
рительному преобразованию матрицы А к виду (8.35) существенная эко­
номия числа арифметических операций недостаточна для практического
использования QR-алгоритма. Дело в том, что при наличии близких
соседних собственных значений Л.; "" Л.; _ 1 элемент hi~J- 1 убывает очень
медленно пропорциональноqk, где q = 1 ~1 :::::; 1. Для решения этой про-
Л, _ 1
блемы используют различные варианты QR-алгоритма со сдвигами.
Поясним суть этого подхода. Допустим, что для Л. 1 известно хорошее
приближение л.;. Тогда собственными значениями матрицы jj(k) =
282

284. § 8.4. QR-алгоритм
= Jl(k>-Л.jE являются 7i..j= Л.г л.; ,j = , 2, ..., т. В этом случае вместо
Л·
отношения ' ~ 1 скорость убывания поддиагонального элемента
Л;_ 1
- .-щ Л; Л; - Л.;
h i. i- 1 определяет величина --- = • ~ О. После нескольких ите-
Л; _ 1 Л.;_ 1 -Л,
-щ
раций QR-алrоритма, которые практически сделают элемент h ;, ;_1
равным нулю, следует выполнить обратный сдвиг, положив H(k) =
= fiщ + Л.jЕ. После выполнения этой операции матрицы А и н<k> снова
имеют общий набор собственных значений.
Последовательное осуществление сдвигов для i = т, т - 1, ..., 1,
сопровождаемых итерациями по QR-алгоритму, дает возможность
быстро привести матрицу А к виду (8.33). Остающийся невыясненным
вопрос о том, как получить приближенные значения л.; ~ Л.;, снимается,
если учесть, что в ходе QR-алrоритма диагональные элементы h~;> схо­
дятся к Л; при k-+ оо. Следовательно, в качестве л.; можно, например,
брать элементы 1 h;;>.
Итак, прежде чем применять QR-алгоритм, следует преобразовать
исходную матрицу А к форме Хессенберга. Без такого преобразования
QR-алгоритм практически не применяется. Затем целесообразно
использовать один из вариантов QR-алгоритма со сдвигами.
Пусть теперь собственные значения найдены и требуется найти
один собственный вектор ej матрицы А, отвечающий собственному зна-
чению Л.j, или несколько собственных векторов. Тогда целесообразно
сначала найти соответствующий собственный вектор vj матрицы Н
(например, методом обратных итераций), а затем вычислить ej по
формуле ej = Р · vj, где Р - матрица подобия из (8.36).
Замечание 1. Вычисление собственного вектора ej непосред­
ственным применением метода обратных итераций к матрице А
возможно, но потребует большего числа арифметических опера­
ций по сравнению с указанным выше подходом.
1 Чаще всего в библиотечных програм1ах используется либо указанная стратегия
сдвигов (сдвигов по Рэ~ею), либо стратегия сдвигов по Ун.1кинсону (103].
283

285. Глава 8. Методы решения nроблемы собственных значений
Замечание 2 Проведенное в этом параграфе обсуждение алго­
ритма носило в значительной степени ознакомительный характер.
Практически не был затронут случай, когда матрица имеет кратные
или комплексные собственные значения Не рассматривались и осо­
бенности применения QR-алгоритма для комплексных матриц.
Замечание 3 QR-алгоритм обладает хорошей обусловленно­
стью Например, как показано в (23], в одном из его вариантов после
числа итерации, не превосходящего 5, для каждого собственного зна-
чения получаются приближения А.~, л.;, ...,л.:, являющиеся точны­
ми собственными значениями некоторой матрицы А., такой, что
llA-A.llE ;$ 30т2 &JAllE,
(это утверждение сформулировано в терминах обратного анализа
ошибок).
§ 8.5. Допо.nните.nьные замечани1
1. В данной книге не рассмотрены некоторые весьма популярные
методы решения проблемы собственных значений. Изложение метода
бисекций, метода вращении Якоби, QL-алгоритма (являющегося вари­
антом QR-алгоритма), LR-алгоритма и других методов можно найти,
напри>.1ер в (23, 24, 31, 75, 102, 103].
Авторы советуют обратить внимание на книги (49, 25•], содержащие
изложение современных численных методов решения проблемы собст­
венных значений (в том числе, подробное обсуждение QR-алгоритма),
вполне доступное для студента или выпускника технического вуза.
2. Если А - заполненная матрица общего вида умеренного
порядка, то лучшим выбором для вычисления всех собственных зна­
чений служит один из вариантов QR-алгоритма со сдвигами. Необ­
ходимо только предварительно преобразовать матрицу к форме Хессен­
берга Часто до этого производится уравновешивание (или
масштабирование) матрицы (49]
3 Когда А - симметричная матрица умеренного порядка, ее
обычно приводят сначала с помощью последовательных преобразо­
ваний Хаусхолдера к трехдиагональному виду. Для вычисления собст­
венных значений полученной трехдиагональной матрицы можно
использовать QR-алгоритм, но, по-видимому, чаще более предпочти­
тельным является метод бисекций Одно из достоинств этого алго­
ритма, состоит в том, что он позволяет находить не все собственные
значения, а одно или группу нужных собственных значений.
284

286. § 8.5. Дополнительные замечания
4 Если приближенное значение собственного числа найдено, то
подходящим методом вычисления соответствующего собственного
вектора является метод обратных итераций
5 Методы, которые используются в настоящее время для решения
проблемы собственных значений, когда А - разреженная матрица
большой размерности, можно разделить на две основные группы
методы одновременных итераций (или итерирования подпространства)
и методы типа Ланцоша Их обсуждение можно найти, например в [31,
49]. Один из простейших возможных подходов - степенной метод -
был рассмотрен в § 8.2
285

287. Глава 9
МЕТОДЫ ОДНОМЕРНОЙ МИНИМИЗАЦИИ
Одно из важнейших направлений в конструировании изделий, а также
проектировании и эксплуатации технологических процессов состоит
в оптимизации (минимизации или максимизации) некоторой характери­
стики /(х). Функцию /(х) часто называют целевой функцией. Заметим,
что основное внимание может быть уделено минимизации целевой
функции, так как максимизация сводится к минимизации с помощью вве-
дения новой целевой функции f (х) = -f(x). Когда варьируется один ска­
лярный параметр х, возникает задача одномерной минимизации.
Необходимость изучения методов решения задачи одномерной
минимизации определяется не только тем, что задача может иметь
самостоятельное значение, но и в значительной мере тем, что алго­
ритмы одномерной минимизации являются существенной составной
частью алгоритмов решения задач многомерной минимизации (см. гл.
1О), а также других вычислительных задач.
§ 9. 1. Задача одномерной минимизации
1. Постановка задачи. Определения. Пусть f(x) - действительная
функция одной переменной, определенная на множестве Х с (-оо, оо).
Напомним, что точка х Е Х называется точкой глобального минимума
функции f на множестве Х, если для всех х Е Х выполняется нера­
венство f(x) ~ /(х). В этом случае значение f(x) называется мини­
мальным значением функции f на Х.
Точка х Е Х называется точкой локального минимума функции /,
если существует такая о-окрестность этой точки, что для всех х из мно­
жества Х, содержащихся в указанной о-окрестности, выполняется нера-
венство f( х )~ f(x). Если же для всех таких х, не совпадающих с х
выполняется неравенство f( х) < j(x), то х называется точкой
строгого локального минимума.
Пр им ер 9.1. Для функции, график которой изображен на рис. 9. 1,
точки :Х 3 и :Х4 являются точками строго локального минимума, а в
точках х, удовлетворяющих неравенству х 1 ~ х ~ :Х 2 , реализуется
нестрогий локальный минимум. .&
286

288. § 9.1. Задача одномерной минимизации
х
Рис. 9.1
Известно, что необходимым условием того, чтобы внутренняя для
множества Х точка х была точкой локального минимума дифференци­
руемой функции/, является выполнение равенства
f'(x) =о. (9.1)
Число х ,удовлетворяющее этому равенству, называется стационарной
точкой функции f Конечно, не всякая стационарная точка х обязана
быть точкой локального минимума. Для дважды непрерывно диффе­
ренцируемой функции достаточным условием того, чтобы стацио-
нарная точка х была точкой строгого локального минимума, является
выполнение неравенства f"(x) >О.
Существуют различные постановки задачи минимизации. В самой
широкой постановке требуется найти все точки локального минимума и
отвечающие им значения функции f В приложениях чаще всего воз­
никает задача вычисления конкре1 ной точки локального минимума или
точки глобального минимума. Иногда представляет интерес только
лишь минимальное значение целевой функции, независимо от того,
в какой именно точке оно достигается.
2. Отрезок локализации. Подобно тому, как алгоритмы решения
нелинейных уравнений настроены на отыскание одного изолированного
корня (см. гл. 4), большинство алгоритмов минимизации осуществляет
лишь поиск точки локального минимума функции f Для того чтобы при­
менить один из таких алгоритмов минимизации, следует предварительно
найти содержащий точку х отрезок [а, Ь], на котором она является един­
ственной точкой локального минимума. Этот отрезок в дальнейшем
будем называть отрезком локализации 1 точки х .К сожалению, не суще­
ствует каких-либо общих рецептов относительно того, как найти отрезок
локализации. В одномерном случае полезным может оказаться табулиро-
1 В теории оптимизации отрезок [а, Ь] чаще называют интервалом неопределенности.
Мы понимаем интервал неопределенности иначе (см. § 9.2).
287

289. Глава 9. Методы одномерной минимизации
вание функции с достаточно мелким шагом и (или) построение
графика. Отрезок [а, Ь] может быть известен из физических сообра­
жений, из опыта решения аналогичных задач и т.д. Для некоторых алго­
ритмов (например, для метода Ньютона) достаточно иметь не отрезок
локализации, а хорошее начальное приближение х<0> к х .
Пр им ер 9.2. Для функции f(x) = х3 - х + e-r, произведем локали­
зацию точек локального минимума.
Из графика функции, изображенного на рис. 9.2, видно, что функция
f(x) имеет две точки локального минимума х 1 и х2 , первая из которых
является и точкой глобального минимума. Для точки х 1 за отрезок лока­
лизации можно принять отрезок (-4, -3), а для точки х 2 - отрезок [О, 1).
Докажем теперь, что на отрезке (О, 1) действительно содержится
точка локального минимума. Для этого заметим, что f'(x) = 3х2 - 1 - е-х
и f'(O) = -2 <О, f'(l) = 2 - е-1 >О. Так как значения /'(О) и f'(l) имеют
разные знаки, то на отрезке (О, 1] содержится точка х ,для которой
f'(x) = О. Но /"(х) = бх + е-х > О для всех х е (О, 1). Следовательно,
у
з 4 х
Рис. 9.2
288

290. § 9.1. Задача одномерной минимизации
/"(х) > О и точка х на отрезке [О, 1] есть единственная точка
локального минимума. Аналогично доказывается, что отрезок [--4, -3]
также является отрезком локализации. .А.
3. Унимодальные функций. Пусть f - функция, определенная на
отрезке [а, Ь]. Предположим, что на этом отрезке содержится единст-
венная точка х локального минимума функции f, причем функция
строго убывает при х ~ х и строго возрастает при х <:: х .Такая функция
называется унимодальной 1. Возможны три случая расположения точки
х на отрезке [а, Ь]: точка х является внутренней для отрезка, х сов­
падает с левым концом отрезка и х совпадает с правым концом
отрезка. Соответственно и график унимодальной функции может иметь
одну из форм, схематично изображенных на рис. 9.3.
а ь х Q ь х
а) б) в)
Рис. 9.3
Замечание. Унимодальная функция, вообще говоря, не обя­
зана быть непрерывной. Например, функция, изображенная на
рис. 9.4, унимодальна и имеет три точки разрыва.
~
1 r1
м1 1
1 1
Рис. 9.4
х
1 Иногда такую функцию называют строго унимодальной, а унимодальной называют
функцию, которая строго убывает nри х $ х 1 , равна постоянной nри х 1 $ х $ х2 и строго
возрастает nри х ~ х 2 [20).
289

291. Глава 9. Методы одномерной минимизации
Приведем достаточное условие унимодальности функции на
отрезке [а, Ь].
Предложение 9.1. Если для всех х Е [а, Ь] выполнено условие
/"(х) >О, то функция унимодальна на отрезке [а, Ь]. •
Пр им ер 9.3. Функция /(х) = х3 - х + е-х унимодальна на каждом из
отрезков [-4, -3] и [О, 1]. Чтобы убедиться в этом, достаточно заметить,
что/"(х) = 6х +е-х >О для всех х Е [-4, -3], х Е [О, 1], и воспользо­
ваться предложением 9.1. •
Для сужения отрезка локализации точки минимума унимодальной
функции полезно использовать следующее утверждение.
Предложение 9.2. Пусть f - унимодальная на отрезке [а, Ь]
функция и а $ а < у < 13 $ Ь. Тогда:
1° если /(а)$ /(/3), то х Е [а, j3];
2° если /(а)~ /(/3), то х Е [а, Ь];
3° если /(а)~ /(у) и /(у)$ /(/3), то х Е [а, /3].
Доказательство. 1°. Предположим противное: х > 13. Тогда
вследствие унимодальности f получим /(а) > /(/3), что противоречит
условию.
2°. Предположим противное: х < а. Тогда вследствие уиимодаль­
ности /получим /(а)< /(/3), что противоречит условию.
3°. В силу п. 1° имеем х Е [а, j3], а в силу п. 2° имеем х Е [а, Ь].
Следовательно, х Е [а, /3].
Геометрическая иллюстрация пп. 1° и 2° приведена на рис. 9.5. •
1 1
11 :r а ь х
Нов•1й отрезок Новый отрезок
а) б)
Рис. 9.5
290

292. § 9.1. Задача одномерной минимизации
Многие алгоритмы одномерной минимизации построены в расчете
на то, что на отрезке локализации целевая функция унимодальна. В
частности, такими являются алгоритмы, рассматриваемые в § 9.3.
4. Об одном подходе к локализация точки минимума. На
практике часто бывает неизвестно, является ли данная функция унимо­
дальной. Однако во многих случаях из дополнительных соображений
следует, что при х ~ х0 функция f сначала убывает, а затем, начиная с
некоторого значения х = х, становится возрастающей (правда, не
исключено, что далее она снова может стать убывающей). Для того
чтобы в таком случае локализовать точку х , используют различные
нестрогие методы. Один из распространенных подходов состоит в сле­
дующем. Выбирают начальный шаг h > О, в несколько раз меньший
предполагаемого расстояния от точки х0 до точки х .Затем вычисляют
и сравнивают значения f(x0) и f(x1), где х 1 = х0 + h.
Если оказывается, что f(x0) > f(x 1), то последовательно вычисляют
значения функции f в точках xk = х0 + 2k - 1h для k ~ 2. После обнару­
жения первой же точки, для которой f(xk) ~ f(xk + 1), за отрезок локали­
зации принимают отрезок [xk- 1, xk+ 1]. В случае, изображенном
на рис. 9.6, а, за отрезок локализации принят отрезок [х2, х4].
Если же f(x0) ~ f(x1), то последовательно вычисляют значения
в точках xk = х0 + h/2k - 1, k ~ 2. После обнаружения первой же точки х"'
для которой f(xk) < /(хо), за отрезок локализации принимают отрезок
f(x0)
',,_,,
о) б)
Рис. 9.б
291

293. Глава 9. Методы одномерной минимизации
Таблица 9.1
k о 1 2 3 4 5
xk -5 -4 8 -46 -4 2 -3 4 -1 8
f(xk) 28 4 15 7 6 74 -3 30 -5 94 2 02
[х0, xk _ 1). В случае, изображенном на рис. 9.6, б, за отрезок локали­
зации принят отрезок [х0, х2].
Описанный метод не является строгим и не гарантирует, что отрезок
локализации всегда будет найден. Например, для функции, график
которой изображен штрихами на рис. 9.6, а, при выбранном шаге h
справедливы неравенства f(x0) > f(x1) > /(х2) > /(х3) > f(x4) и поэтому
отрезок локализации точки х обнаружен уже не будет. Тем не менее
этот или близкий к нему методы часто используются на практике.
Пр им ер 9.4. Локализуем указанным выше образом точку
локального минимума функции f(x) = х3 - х + е-х.
Возьмем х0 = -5, h = 0.2 и положим х1 = х0 + h = -4.8. Так как /(х0) :::::
::::: 28.4 > /(х 1 ) ::::: 15.7, то будем последовательно вычислять значения
функции f в точках xk = х0 + 2k - 1h. Из табл. 9.1 видно, что при k = 4
впервые выполняется неравенство f(xk) < f(xk ... 1). Поэтому за отрезок
локализации следует принять отрезок [х3, х5] = [-4.2, -1.8). А
§ 9.2. Обусnовnенность задачи минимизации
Пусть х - точка строгого локального минимума функции f, вычис­
ляемой с погрешностью. Будем считать, что в некоторой окрестности
точки х вычисляемые приближенные значения /* (х) удовлетворяют
неравенству 1/(х) - ](х) / ::; Л = Л(f*), т.е. имеют границу абсолютной
погрешности, равную Л. Как нетрудно понять, существует такая малая
окрестность (х - Е, х + Е) точки минимума х, для которой, основы­
ваясь на сравнении вычисляемых значений ] (х), нельзя достоверно
определить ту точку, в которой действительно достигается минимум
функции/ Эта ситуация схематично изображена на рис. 9.7. Интервал
(Х - Е, Х + Е ) будем называть интервалом неопределенности точки Х
локального минимума.
292

294. § 9.2. Обусловленность задачи минимизации
Х-Е Х х+[
Рис. 9.7
Оценим значение ё радиуса интервала неопределенности в предпо­
ложении, что функция f дважды непрерывно дифференцируема и
выполнено условие f"(x) >О. В этом случае с учетом того, что f'(x) =О,
для значений функции f в точках х, близких к х ,справедливо прибли­
женное равенство
/"(х)
f(x) ~ f(x) + - - (х- х)2 •
2
-Оценим минимальное расстояние между точками х и х , начиная
с которого заведомо будет выполнено неравенство ](х) > t•(x), т.е.
точка х перестанет попадать в интервал неопределенности. Имеем
f"(x)-/*(x)=f(x)-f(x) + (f·(x)-f(x))- (f·(x)-f(x)) ~
- f"(x) -
~f(x)-f(x)-2л~-2- (х-х)2 -2Л.
Следовательно,
t•(x)-f*(x) ~f"~x) (х-х)2 -2Л
и неравенство /•(х) > f"(x) выполнено, если (х - х)2 ~ 4Л//"(х).
Таким образом,
ё ~ 2JЛ/f"(х). (9.2)
Заметим, что любое приближение х• к х, попавшее в интервал неоп­
ределенности, нельзя отличить от точного значения х точки минимума,
используя только вычисляемые значения ] функции f Поэтому
Л(х*} ~ 2Jлif*}lf"<x>. (9.3)
293

295. Глава 9. Методы одномерной минимизации
Итак, рассматриваемую задачу минимизации нельзя назвать хорошо
обусловленной. Если задача хорошо масштабирована, т.е. х - 1,
lf(x) - , f'(x) - ,то соотношение (9.3) можно записать в терминах
относительных погрешностей так:
8(.t")- JБ(f*).
Отсюда следует, что если 8(!*) - 10-т, то 8(х*) - 10-т12 . Иными
словами, если значения функции вычисляются с т верными значащими
цифрами, то приближенное значение точки минимума можно найти
примерно лишь с т/2 верными значащими цифрами.
Таким образом, точность определения положения точки минимума
гладкой функции существенным образом зависит от точности вычис-
ления значений функции f. При этом если для поиска х используются
только приближенные значения /*(х), вычисляемые для различных х, то
неизбежна потеря примерно половины верных значащих цифр.
Предположим теперь, что для отыскания точки локального
минимума можно использовать вычисляемые каким-либо образом при­
ближенные значения (/')*(х) производной функции f Как уже отме­
чалось в § 9.1, в рассматриваемом случае задача минимизации эквива-
лентна задаче отыскания корня х нелинейного уравнения /'(х) = О. Из
результатов § 4.2 вытекает, что последняя задача обладает значительно
меньшей чувствительностью к погрешностям. В частности, спра­
ведлива следующая оценка границы абсолютной погрешности:
- -· 1 - •
Л(х ) ""-(-) Л((f') ) .
!" х
(9.4)
Сравнение (9.4) с оценкой (9.3) показывает, что алгоритмы, исполь­
зующие для отыскания решения х уравнения (9.1) вычисление зна­
чений производной, могут достигать более высокой точности, чем алго­
ритмы, использующие для минимизации функции f только вычисление
ее значений.
Пр им ер 9.5. Оценим радиус интервала неопределенности для
каждой из точек х 1 ""-3.7, х 2 ""0.7 локального минимума функции
f(x) = х3 - х + е-х в случае, когда вычисление функции производится
на 6-разрядном десятичном компьютере 1•
1 Напомним, что 6-разрядНЫ1 десятичным компьютером мы условились называть
гипотетический компьютер, имеющий шесть десятичных разрядов мантиссы и произво­
дящий округление по дополнению.
294

296. § 9.2. Обусловленность задачи минимизации
Заметим, что f(x 1) "'/(-3.7) "'-6.5, f(x 2) "'/(0.7) = 0.14. Так как
для используемого компьютера 1 Ем= 5 • I0-7, то в малой окрестности
точки х 1 верхняя граница Л1 абсолютной погрешности вычисления f
приближенно равна
Ем lf(x1)1 "'5 · 10-7 • 6.5 = 3.25 · 10-6.
Аналогично,
Вычисляя значения второй производной f"(x) = 6х + е-х при х = х 1,
х= х 2 ,получаемf"(х 1 ) "'18,f"(x2) =4.7.Всилуформулы(9.2)радиусы
интервалов неопределенности оцениваются следующим образом:
&1"'2JЛ1/f"(х 1 ),., 2J3.25 • 10-6118,., s· 10-4,
Ё2 "'2JЛ2//"(х2) "'2J7 · J0-8/4.7"' 2 · J0-4.
Следовательно, точку х 2 можно найти с большей точностью, чем
точку х 1, если использовать сравнение вычисляемых на 6-разрядном
десятичном компьютере значений функции f. При этом каждую из
точек можно найти с точностью Е = J0-3, но вряд ли удастся найти с
ТОЧНОСТЬЮ Е = JО-4. А
Пр им ер 9.6. Пусть теперь точки х 1 и х 2 локального минимума
функции /(х) = х3 - х + е-х ищутся как решения нелинейного уравнения
/'(х) = 3х2 - 1 - е-х = О. (9.5)
-
Оценим радиус интервала неопределенности для каждой из точек х 1,
х 2 , если вычисления ведутся на том же компьютере, что и в примере 9.5.
Оценим сначала границу абсолютной погрешности вычисления про­
изводной исходя из приближенного равенства
Л=Л(f')=Л(3 х 2 ) + Л(I) + Л(e-i)"' Ем(Зх2 + e-i).
Тогда
Л1=Ем(Зх~+е-:х 1 )"4·JО-5 , Л2 "'Ем(Зх;+е-:т2 )"'JО-6.
1 Напомним, что через &м обозначено машинное эпсилон - величина, характеризую­
щаJ1 относительную точность представлениJ1 чисел в компьютере.
295

297. Глава 9. Методы одномерной минимизации
На основании формулы (9.4) имеем
E1""Л1/f"(x,):::::2· J0-6 , Е1:::::Л2//"(х2):::::2• JО-1 . (9.6)
Заметим, что погрешности представления чисел х 1 , х 2 на 6-раз­
рядном десятичном компьютере таковы: i:" I х 11 ::::: 2 · 1о-6 , i:" I х2 1 :::::
::::: 4 · 10-1. Поэтому полученные оценки (9.6) означают, что. решая урав­
нение (9.5), можно найти точки х 1 и х 2 с максимальной для исполь­
зуемого компьютера точностью, равной соответственно 2 · 10- 6 и 4 · 10-7
(ер. с результатом примера 9.5). .А.
§ 9.3. Методы пр1моrо поиска.
Оптимальный пассивный поиск.
Метод депени1 отрезка пополам.
Методы Фибоначчи и эопотоrо сечени1
Ряд методов минимизации основан на сравнении значений функции
/, вычисляемых в точках х 1 , х2, ..., хн- Эти методы часто называют
методами прямого поиска, а точки х, - пробными точками.
Прежде чем перейти к изложению некоторых из наиболее известных
методов прямого поиска, уточним постановку задачи. Будем считать,
что требуется найти приближение х • к точке минимума х унимо­
дальной на отрезке [а, Ь] функции/. Предположим также, что число
пробных точек N заранее фиксируется и за приближение .х• к точке
минимума принимается одна из этих точек.
1. Оптимальный пассивный поиск. Метод решения поставленной
задачи, в котором задается правило вычисления сразу всех пробных
точек х1 , х2, ... , хн и за .х· принимается та точка xk, для которой f(xk) =
min /(х,), называется методом пассивного поиска. Соответст-
1,; 1,; .v
вующая геометрическая иллюстрация приведена на рис. 9.8.
xk-I xk xk+I хн Ь х
Рис. 9.8
296

298. § 9.3. Методы прямого поиска
Оценим погрешность этого метода. Для удобства положим х0 = а,
xN+ 1 = Ь и будем считать, что х0 Sx1<х2 < ... <xNSxN+ 1 • В силу выбора
точки :х• = xk справедливы неравенства f(xk- 1) ~ f(xk) и f(xk) $ f(xk + 1).
Поэтому из п. 3° предложения 9.2 следует, что х Е [xk _ 1, xk+ 1]. Значит
lx-xkl :;;max{xk-xk_ 1,xk+ 1 -xk}.
Так как положение точки минимума х на отрезке [а, Ь] заранее неиз­
вестно, то для :х· = xk справедлива лишь следующая гарантированная
оценка погрешности:
lx-x•I $ max lx,-x,_ 11. (9.7)
1$1$N+1
Можно показать, что величина, стоящая в правой части неравенства
(9.7), станет минимальной, если точки х 1 , х2, ••• , xN расположить на
отрезке [а, Ь] равномерно в соответствии с формулой х, =а+ ih, где h =
= Л/(N + 1), Л = Ь - а. Метод с таким выбором пробных точек назы­
вается оптимальным пассивным поиском. Гарантированная оценка
погрешности для него выглядит так:
1
- -.
1
Ь-а Л
х-х :;;--=--.
N+I N+I
(9.8)
Пр им ер 9.7. Используем оптимальный пассивный поиск для того,
чтобы найти с точностью Е = 0.1 точку х локального минимума
функции f(x) = х3 - х + е-х, локализованную на отрезке (О, 1].
Из (9.8) следует, что для решения задачи потребуется вычислить зна­
чения функции в девяти пробных точках вида х, = 0.1 i, где i = 1, 2, ..., 9.
Приведем таблицу этих значений (табл. 9.2).
Таблица 9.2
х 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
у 0.81 0.63 0.47 0.33 0.23 0.17 0.14 0.16 0.24
Так как минимальное значение достигается в точке х1 = 0.7, то х =
= 0.7 ± 0.1. Если бы мы попытались найти х с точностью Е = 10-2, то
оптимальный пассивный поиск потребовал бы вычисления значений
функции уже в 99 точках. .&
2. Метод делении отрезка пополам. Пусть для решения постав­
ленной задачи последовательно вычисляются значения функции f в N
пробных точках х 1 , х2, ••• , х№ причем для определения каждой из точек
xk можно использовать информацию о значениях функции во всех пре-
297

299. Глава 9. Методы одномерной минимизации
дыдущих точках х 1 , х2, "., xk _ 1• Соответствующие методы называют
методами последовательного поиска. Рассмотрим простейший из
методов этого семейства - метод деления отрезка пополам. В нем,
как и в двух других рассматриваемых в этом параграфе методах
{методах Фибоначчи и золотого сечения), используется принцип после­
довательного сокращения отрезка локализации, основанный на предло­
жении 9.2 и на следующем простом утверждении.
Предложение 9.3. Если функция унимодальна на отрезке [а, Ь],
то она унимодальна и на любом отрезке [с, d] с [а, Ь]. •
Для удобства изложения обозначим отрезок [а, Ь] через [а<О>, ь<О>].
Поиск минимума начинают с выбора на отрезке[а<0>, ь<0>] двух симмет­
рично расположенных точек
,...(О) -- а(О) + Ь(О) (0) а(О) + Ь(О)
"' 2 - cS, 13 = 2 + cS.
Здесь О < cS < (Ь - а)/2, cS - параметр метода. Далее вычисляют зна­
чения /{а<0>) и /(13<0>). Сравнение этих значений в силу предложенИJI
9.2 позволяет сократить отрезок локализации следующим образом:
если /{а<0>) ~ /(13<0>), то х е [а(!), ь< 1>] = [а<О>, 13<0>];
если /(а<О)) > f{l3(0)), ТО Х Е [а(!), b(l)] = [а(О), Ь(О)].
Если описанную процедуру принять за одну итерацию метода
и продолжить аналогичные операции для построения последователь­
ности сокращающихся отрезков локализации, то получим итерационный
метод. Опишем очередную его итерацию исходя из того, что отрезок
локализации [dk b(k)] уже найден.
Выполняют следующие действия:
) ВЫЧИСЛЯЮТ
a(k) =a(k) + b(k) - cS' f.l(k) =a<k) + ь<k) + cS.
2 t' 2 ,
2) находят значения j(a<k>) и j(13<k>);
3) новый отрезок локализации определяют по правилу:
если /{а<*>)~ f(l3<k>), то [а<*+ 1>, ь<k+ 1>] = [а<*>, 13<*>];
если /{а<*>)> /(13<*>), то [a<k +1>, ь<k + 1>] =[а<*>, ь<*>].
В первом случае за очередное приближение к точке минимума при­
нимают x<k+ l) = a(k), а во втором случае x<k+ I) = 13<*> (рис. 9.9).
Обозначим через л<п> = ь<п> - а<п) длину отрезка [а<пJ, ь<п>]. Как
нетрудно заметить, справедливо равенство
298
л<п)
л<п+1>=2+Б. (9.9)

300. § 9.3. Методы прямого поиска
2Б
,_....._,
0 <k)--------..------ь<k)
1 a<kJ 1 1p(k) 1
1 1 1 1
1 1 1 1
1 1
: 0 (k+I) : a(k+I) p<k+I) Ь (k+I)
: : Первый
1 1 случай
0 (k+) a(k+I) p<k+I) Ь (k+I)
Второй
случай
Рис. 9.9
Поэтому, если параметр cS достаточно мал (cS « д<п>), то длина вновь
полученного отрезка почти вдвое меньше длины предыдущего отрезка.
Отсюда - и название метода.
Использовав равенство (9.9), с помощью метода математической
индукции легко показать, что
д<п> = (л - 2Б) + 2о.
2п
Заметим, что д(п) убывает и при п -+ оо стремится к значению 2cS,
оставаясь при каждом п больше него. Поэтому сделать при некотором п
длину д<п> отрезка локализации [а<п>, ь<п>] меньше заданного Е > О
можно лишь, выбрав о < Е/2. В этом случае из очевидной оценки
погрешности lх<п> - х 1 < д(п) следует, что значение х действительно
можно найти с точностью Е и справедлив следующий критерий окон­
чания итерационного процесса. Вычисления следует прекратить, как
только окажется выполненным неравенство
Д(n) ~ Е. (9.1 О)
Тогда за приближение к х с точностью Е можно принять :х· = x<n>.
Замечание. При реализации метода на компьютере необхо­
димо учитывать, что вычисления значений функции/ будут произ­
водиться с погрешностью. Для того чтобы знак разности /°(а<п>) -
- f°(~<п>) совпадал со знаком разности f(а<п>) - f(~(nJ), необхо-
димо, чтобы выполнялось условие о ;;::::; & (см. равенство (9.2)).
Поэтому о нельзя задавать слишком малым.
Пр им ер 9.8. Применив метод деления отрезка пополам, найдем
с точностью Е = 10-2 точку х локального минимума функции f(x) = хз -
299

301. Глава 9. Методы одномерной минимизации
Таблица 9.3
п a<•I ь<•) a<•J j(a(•I) 13<•) /(13<•1) л<•~
о 0.000000 1.000000 0.499000 о 232389 0.501000 0.230676 1.000
1 0.499000 1.000000 0.748500 0.143924 0.750500 0.144350 0.501
2 0.499000 0.750500 0.623750 0.154860 0.625750 0.154131 0.252
3 0.623750 0.750500 0.686125 0.140403 0.688125 0.140230 0.125
4 0.686125 0.750500 0.717088 0.139821 0.719088 0.139940 0.063
5 0.686125 0.719088 0.701607 0.139549 0.703607 0.139520 0.033
6 0.701607 0.719088 0.708348 0.139543 0.711348 0.139587 0.017
7 0.710141 0.719813 - - - - 0.010
-х + е-х локализованную на отрезке [О, l]. Вычисления будем вести на
6-разрядном десятичном компьютере.
Зададим о = 1о-3, а<0> = О, Ь(О) = l.
1-я итерация.
l. Вычислим:
а(О) + Ь(О) а(О) + Ь(О)
а<0>= 2 -о=О.499, р<0>= 2 +о=О.501.
2. Определим значения f(a<0>)::::: 0.232389, /(13<0>)::::: 0.230676.
3. Так как f(a<0>) > лр<0>), то следует положить [a(I>, b(I)] = [0.499, 1].
Результаты следующих итераций приведены в табл. 9.3.
Так как л(7) ~ &, то при п = 7 итерации прекратим и положим х :::::
::::: р<п> = 0.711348. Таким образом, х = 0.71±0.01. Заметим, что для дос­
тижения точности & = l0-2 потребовалось 14 вычислений функции. .А.
3. Метод Фибоиаччи. Заметим, что метод деления отрезка пополам
требует на каждой итерации вычисления двух новых значений
функции, так как найденные на предыдущей итерации в точках а<п> и
р<п> значения далее не используются. Обратим теперь внимание на то,
что одна из этих точек (обозначенная в предыдущем пункте через х<п>)
является внутренней для отрезка [а<п>, ь<п)] и поэтому дальнейшее
сокращение отрезка можно произвести, вычислив дополнительно зна­
чение функции лишь в одной новой точке. Это наблюдение приводит к
методам, требующим на каждой итерации (кроме первой) расчета лишь
одного нового значения функции f Два наиболее известных среди них -
методы Фибоначчи и золотого сечения.
300

302. § 9.3. Методы прямого поиска
Метод Фибоначчи 1 является оптимальным последовательным
методом, т.е. методом, обеспечивающим максимальное гарантиро­
ванное сокращение отрезка локализации при заданном числе N вычис­
лений функции. Этот метод основан на использовании чисел Фибо­
наччи Fn, задаваемых рекуррентной формулой
Fn = Fn _ 1 + Fn _2 (п Z 2)
и начальными значениями F0 = 1, F 1 = 1. Укажем несколько первых
чисел: F0 = 1, F 1 = 1, F2 = 2, F3 = 3, F4 = 5, F5 = 8, F6 = 13, F7 = 21,
F8 = 34, F9 = 55, F10 = 89, F11 = 144.
Метод Фибоначчи состоит из N - 1 шагов. Очередной (k + 1)-й шаг
выполняют здесь аналогично (k + 1)-й итерации метода деления отрезка
пополам. В отличие от него точки a<k ~(k) здесь находят по формулам
F F
a(k) = a(k) + ~ Л(k) ~(k) =a<k> + ~ Л(k).
FN-k+ 1 FN-k+ 1
Новый отрезок локализации определяют по тому же правилу:
если f(a(k)) $ f(~(k)~ то [a<k + 1), b(k + 1)] = [a<k>, ~(k)];
если f(a<k)) > f(p<k>), то [a<k + 1), ь<k+ 1)] = [a<k>, ь<k>].
В первом случае за очередное приближение к точке минимума при­
нимают x<k + 1) = a<k), а во втором случае x<k+ 1>= ~(k) (рис. 9.1 О).
Важно то, что в любом случае точка x<k+ I) совпадает с одной из точек
F
a<k+J)=a(k+l)+ N-k-2 л<k+IJ,
FN-k
F
~(k+ 1) =a<k+ t) + N-k-1 л<k+ 1).
FN-k
а (k)
1а<*> 113<k)
ь<t>
1 1
1 1 1 1
1 1 1 1
1 ;
a<k+) f ll(k+l)
11
1 а (k+)1 ь<k+t>
1 1 1
Первый1 1 1
1 1 1 случай
t ' t t
о (k+J) a<k+I) 13<k+I) ь (k+I/
Второй
случай
Рис. 9.10
1 Фибоначчи (Леонардо Пизанский) (1180--1240)- итальянский математик.
301

303. Глава 9. Методы одномерной минимизации
Поэтому на очередном шаге достаточно вычислить значение функции
лишь в одной недостающей точке.
В результате выполнения N - 1 шагов отрезок локализации умень­
шается в FN + /2 раз, а точка x(N - 1) оказывается центральной для
последнего отрезка локализации [a<N - 1), ь<N - 1)]. Поэтому для x<N - 1)
справедлива следующая оценка погрешности:
1Х - x<N - 1) 1 ~ _l_ Л .
FN+ 1
(9. 11)
Пр им ер 9.9. Применив метод Фибоначчи, найдем с точностью Е =
= 10-2 точку х локального минимума функции /(х) = х3 - х + е-х, лока­
лизованную на отрезке [О, 1]. Вычисления будем вести на 6-разрядном
десятичном компьютере.
Первым среди чисел Фибоначчи, для которого выполняется условие
ЛIFN+ 1 < Е (где Л =),является число F 11 = 144, отвечающее N = 10.
Зададим а<0> = О, Ь(О) = .
Первый шаг.
1. Вычислим
F9 55
а(О) = а(О) + (Ь(О) _ а<0>) - =- "'о 381944
F 11 144 . '
j3(0) = а(О) + (Ь(О) - а<О>) ; 10 = 18~ "'0.618056.
11
2. Определим значения /(а<О>)"' 0.356308, J(J3<0>) "' 0.157028.
3. Так как j(a<0>) > f(j3(0>), то положим [a(I>, b(I)] = [а<О), Ь(О)].
Второй шаг.
1. С учетом того, что аО> = 13<0>"' 0.618056, найдем:
J3<1) =аО> + (b<1)-a0>)F9/F10 "' 0.763889.
2. Вычислим значение /(j3(1>)"' 0.147712.
3. Так как /(аО)) > /(j3(1>), то положим [ащ, Ь<2>] = [a(I>, ЬО>].
Результаты остальных шагов приведены в табл. 9.4.
После девяти шагов вычисления прекращаем и полагаем х "' 13<8>=
= О.708334. Таким образом, х = О. 71 ± О.О 1. Заметим, что для дости­
жения точности Е = 1о-2 потребовалось десять вычислений значения
функции, в то время как при использовании метода деленИJ1 отрезка
пополам необходимо 14 вычислений. 6.
302

304. § 9.3. Методы прямого поиска
Таблица 9.4
п а<•> ь<•> a<•J /(а<•)) pt•) J(p<•>) л<•>
о 0.000000 1.000000 0.381944 0.356308 0.618056 0.157028 1.000
1 0.381944 1.000000 0.618056 0.157028 0.763889 0.147712 0.618
2 0.618056 1.000000 0.763889 0.147712 0.854167 0.194672 0.382
3 0.618056 0.854167 0.708334 0.139527 0.763889 0.147712 0.236
4 0.618056 0.763889 0.673611 0.141905 0.708334 0.139527 0.119
5 0.673611 0.763889 0.708334 0.139527 0.729167 0.140830 0.090
6 0.673611 0.729167 0.694445 0.139805 0.708334 0.139527 0.056
7 0.694445 0.729167 0.708334 0.139527 0.715278 0.139731 0.035
8 0.694445 0.715278 0.701389 0.139553 0.708334 0.139527 0.021
9 0.701389 0.715278 0.708334 - 0.708334 - 0.014
Хотя метод Фибоначчи и оптимален в указанном выше смысле, часто
он неудобен для использования. В частности, это касается возможного
применения поиска Фибоначчи для решения одномерных подзадач в
алгоритмах многомерной минимизации. Здесь нередко эффективность
алгоритма одномерной минимизации оценивается не по тому, какая точ-
ность в значении х получена, а совсем по другим критериям, к которым
метод плохо приспособлен. Например, бывает важно достигнуть мини­
мального значения функции f с некоторой относительной точностью о
либо уменьшить значение f на определенную величину.
Кроме того, число выполняемых итераций заранее фиксируется, что
удобно далеко не всегда.
4. Метод золотого сечения. Из-за указанных недостатков вместо
метода Фибоначчи чаще используется теоретически почти столь же
эффективный метод золотого сечения.
Напомним, что золотым сечением 1 отрезка называется такое раз­
биение отрезка на две неравные части, что отношение длины всего
отрезка к длине его большей части равно отношению длины большей
части к длине меньшей части отрезка.
Золотое сечение отрезка [а, Ь] осуществляется каждой из двух сим­
метрично расположенных относительно центра отрезка точек
2 2
а=а+-- (Ь-а), ~=а+-- (Ь-а)
3+Js 1+Js
1 Термин «Золотое сечение» ввел Леонардо да Винчи. Принципы золотого сечения
широко использовались при композиционном построении многих произведений мирового
искусства (в особенности, архитектурных сооруженнй античности и эпохи Возрождения).
303

305. Глава 9. Методы одномерной минимизации
~
а а ~ Ь
(9.12) Рис. 9.11
(рис. 9.11 ). Действительно, как нетрудно проверить,
b-a=b-a=J+j5 b-a=p-a=J+j5
Ь-а а-а 2 р-а Ь-р 2
Замечательно то, что точка а осуществляет золотое сечение не
только отрезка [а, Ь], но и отрезка [а, j3]. Действительно,
p-a=~=1+J5
а-а р-а 2
Точно так же точка 13 осуществляет золотое сечение не только отрезка
[а, Ь], но и отрезка [а, Ь]. Этот факт далее существенно используется.
Очередная (k + 1)-я итерация метода золотого сечения производится
аналогично (k + 1)-й итерации метода деления отрезка пополам. В
отличие от него точки a<k>, j3(k) находятся по формулам
2
a<k> = a<k) + - - Л(k)
3 + J5 ,
13<*> = a<k> + _2_ л<k>.
1+Js
Важно то, что какой бы из отрезков [a<kJ, j3(k)] или [a<k>, b(k)] не был
бы выбран за очередной отрезок локализации, точка x<k + 1> (в первом
случаех<k+ I) = a<k>, а во втором случаех<k+ I) = j3<k>) совпадает с одной
из точек а<* + 1), 13<k + 1>. Поэтому на очередном шаге достаточно
вычислить значение функции лишь в одной недостающей точке.
Заметим, что точка х<п> отстоит от концов отрезка [а<п>, ь<п>] на
2
величину, не превышающую ----r; л<п>, поэтому верна оценка
1 + -J5
lx(n)_xl ~-2- Л(п)=Л(п+I),
1 + J5
(9. I2)
которую можно использовать для апостериорной оценки погрешности.
Заметим, что каждая итерация сокращает длину отрезка локализации
в ( 1+ J5 )12 раз. Поэтому ь<п> - а<п> = л<п> = (2/( 1+ J5))пЛ и спра­
ведлива следующая априорная оценка погрешности:
lx<п>-xl ~ - 2- Л.[ ]
п+ 1
1 + J5
(9.13)
304

306. § 9.3. Методы прямого поиска
Таким образом, метод золотого сечения сходится со скоростью гео­
метрической прогрессии, знаменатель которой q = 2/( 1+ J5)"' 0.62.
Пример 9.10. Найдем методом золотого сечения с точностью & =
= 10-2 точку х локального минимума функции f(x) =х3 - х + е-х лока­
лизованную на отрезке [О, 1].
Положим а<0> = О, Ь(О) = 1.
1-я итерация.
1. Вычислим:
а(О) = а<О> + - 2- (ь<0> - а<0>) "' 0.381966,
3 + J5
р<О) = а<О> + - 2- ( Ь(О) - а<О>)"' 0.618034.
1 +Js
2. Найдем f(a(O))"' 0.356280, f(p(O))"' 0.157037.
3. Так как J(a<0>) > лр<О)), то положим (a(l), b(I)] = [а<О>, Ь(О)].
2-я итерация.
. Учтем, что а< 1 > = р<0>"' 0.618034, и вычислим:
p(t) = 0 (1) + - 2- (ЬО>- аО>)"' 0.763936.
1 +Js
2. Определим ЛР(l))"' 0.147725.
3. Так как f(a(l>) =J(p<0>) > /(р< 1 >), то положим [а(2), Ь(2)) =[a(l>, b(l>].
Результаты остальных итераций приведены в табл. 9.5.
Таблица 9.5
п tJ.•) ь<•) а<•) /(а<•)) 13<•) л13<•)> л<•+ 1)
о 0.000000 1.000000 0.381966 0.356280 0.618034 0.157037 0.618
1 0.381966 1.000000 0.618034 0.157037 0.763936 0.147725 0.382
2 0.618034 1.000000 0.763936 0.147725 0.854102 0.194622 0.236
3 0.618034 0.854102 0.708204 0.139526 0.763936 0.147725 0.146
4 0.618034 0.763936 0.673764 0.141883 0.708204 0.139526 0.090
5 0.673764 0.763936 0.708204 0.139526 0.729493 0.140868 0.056
6 0.673764 0.729493 0.695051 0.139774 0.708204 0.139526 0.034
7 0.695051 0.729493 0.708204 0.139526 0.716337 0.139782 О.о21
8 0.695051 0.716337 0.703182 0.139525 0.708204 0.139526 0.013
9 0.695051 0.708204 - - - - 0.008
Так как Л(IО) < &, то итерации следует прекратить и положить х ""
"' а<8> "' О.703182. Таким образом, х = О.70 ± О.О 1. Отметим, что для
достижения точности & = 10-2 потребовалось десять вычислений зна­
чений функции, как и в методе Фибоначчи. .&
305

307. Глава 9. Методы одномерной минимизации
5. Эффективность методов прямого поиска. Эффективность ука­
занных методов можно оценивать, например тем, во сколько раз умень­
шается после использования N вычислений значений функции первона­
чальная длина Л отрезка локализации. Другой критерий - значение
гарантированной оценки погрешности. Данные табл. 9.6 позволяют
сравнить по этим критериям рассмотренные выше методы. Как видно,
очень неэффективен пассивный поиск. Метод деления отрезка пополам
уступает почти эквивалентным по эффективности методам Фибоначчи
и золотого сечения.
Метод прямого поиска
Оптимальный пассивный
поиск
Метод деления отрезка
пополам (N - четное,
величиной 8 пренебрегаем)
Метод Фибоначчи
Метод золотого сечения
Длина отрезка
локализации
2
N+lЛ
2
- - Л ::о 1 7 • (0.62)N • Л
FN+I
- 2 - Л"'16·(062)N•Л[ ]
N- 1
1+Л
Таблица 9.6
Гарантированная
оценка погрешности
"' 0.5 • (0.71 )N • Л
"'0.85 • (062)N • Л
"' (О 62)" · Л
Приведем еще одну таблицу (табл. 9.7), из которой видно, сколько
вычислений значений функции f нужно сделать для того, чтобы дос­
тигнуть точности Е. Предполагается, что начальный отрезок локали­
зации имеет единичную длину.
Таблица 9.7
Метод прямого поиска
Число N при заданном Е, равном
10-1 10-2 10-3 I0-4 10-s
Оптимальный 9 99 999 9999 99999
пассивный поиск
Метод деле.~ия отрезка 6 12 18 26 32
пополам (8 « Е)
Метод Фибоначчи 5 10 15 19 24
Метод золотого сечения 5 10 15 20 24
6. Влияние погрешности вычислений. Одна из самых распро­
страненных ошибок при обращении к стандартным программам, реали-
306

308. § 9.4. Метод Ньютона и другие методы минимизации гладких функций
зующим тот или иной метод на компьютере, состоит в завышении тре­
буемой точности. Необходимо понимать, что при наличии погрешностей
в вычислении значений функции / достижимая точность Е методов
прямого поиска ограничена снизу величиной € ""2JЛ(f*)//"(х), где
€ - радиус интервала неопределенности (см. § 9.2). Это означает,
например, что прямые методы не позволяют найти на 6-разрядном
десятичном компьютере точку х 2 локального экстремума функции
/(х) = х3 - х + е-х с точностью Е < €2 ""2 • I0-4• Задание Е < Е 2 при­
ведет лишь к бесполезной трате машинного времени.
§ 9.4. Метод Ньютона и другие методы
минимизации гладких функций
Отметим, что применение рассмотренных выше методов деления
отрезка пополам, Фибоначчи и золотого сечения не позволяет извлечь
никакой выгоды из возможной гладкости функции. Существуют
методы, которые могут оказаться более эффективными, если миними­
зируемая функция достаточно гладкая. Часть из них является просто
модификациями известных методов решения нелинейных уравнений
(см. гл. 4) применительно к необходимому условию экстремума
/'(х) =О. (9.14)
1. Метод бисекции. Пусть/ - унимодальная непрерывно диффе­
ренцируемая на отрезке [a(OJ, Ь(О)] = [а, Ь] функция и на отрезке [а, Ь]
точка х является единственной стационарной точкой. Применительно
к решению уравнения (9.14) одна итерация метода бисекции выглядит
следующим образом.
Пусть отрезок локализации [a(nJ, ь<п)] известен и найдено значение
х<п) = (а(п) + b(n>)t2. Тогда производят следующие действия:
1) вычисляют значение f'(x<n>);
2) если f'(x(n>) < О, то полагают [а<п + 1), ь<п + IJ] = [х<пJ, ь<пJ]. В про­
тивном случае полагают [а(п + IJ, Ь(п + 1)] = [а<п>, х<п)];
3) вычисляют х<п + 1) = (а<п + 1) + Ь(п + 1))/2.
В рассматриваемом случае метод сходится с оценкой погрешности
(9.15)
и обладает всеми присущими методу бисекции решения нелинейных
уравнений достоинствами и недостатками (см. § 4.3). Возникает лишь
307

309. Глава 9. Методы одномерной минимизации
дополнительная проблема, связанная с необходимостью вычисления
производной f'
2. Метод Ньютона. Для решения уравнения (9.14) можно попы­
таться воспользоваться методом Ньютона (см. § 4.6), расчетная
формула которого в данном случае принимает вид
/'( (n>)
x(n+l)=x(n) __x__ п~О. (9.16)
/"(х(п))'
Следствием теоремы 4.6 является следующее утверждение
Теорема 9.1. Пусть в некоторой окрестности точки х функция
f трижды непрерывно дифференцируема и выполняется условие
f"(x) >О. Тогда найдется такая малая а-окрестность корня х, что
при произвольном выборе начального приближения х(О) из этой сr-окре­
<-тности метод Ньютона (9 16) сходится квадратично. •
В силу сверхлинейной сходимости для метода Ньютона можно
исполь·ювать следующий критерий окончания итераций:
lx(n) _x(n-1)1 < Е. (9.17)
Пример 9.11. Использовав метод бисекции, найдем с точностью
Е = 10-2 точку локального минимума функции /(х) = х3 - х + е Х, лока­
лизованную на отрезке [О, 1].
Положим а<0> = о, Ь(О) = 1, x<0J = (а<0> + ь<0>)12 = о 5. Заметим, ЧТО
f'(x) = 3х2 - 1 - е-х.
1-я итерация.
1) ВЫЧИСЛИМ f'(x<O>)::::: -0.856531;
2) так как /'(х<0>) <О, то [a(I>, ь<I)] = [х<0>, ь<0)];
3) вычислим х< 1 > = (а< 1 > + ь< 1 >)/2 =О 75.
Результаты остальных итераций приведены в табл. 9.8
п tf•) b(ll) x!n) f'(x<·~
о 0.000000 1 000000 0.500000 -0.856531
1 0.500000 1 000000 о. 750000 0.215133
2 0.500000 о 750000 0.625000 -0.363386
3 0.625000 о 750000 0.687500 -0.084863
4 0.687500 о 750000 0.718750 0.062444
5 0.687500 о 718750 о. 703125 -0.011882
6 0.703125 о 718750 0.710938 -
308
Таблица 9.8
(b<•J-a<•>)/2
0.500
0.250
0.125
0.063
0.031
0.016
0.008

310. § 9.4. Метод Ньютона и другие методы минимизации гладких функций
После выполнения шести итераций вычисления можно прекратить
и положить х ::=х<б>. Таким образом, х =0.71±0.01. Отметим, что для
достижения точности t = l0-2 потребовалось шесть вычислений зна­
чения производной /'(х) А
Пример 9.12. Использовав метод Ньютона, найдем с точностью
t = l о-6 точку локального минимума функции /(х) = х3 - х + е-х, лока­
лизованную на отрезке [О, l].
Положим х<О> = 0.5. Результаты вычислений по формуле (9.16),
имеющей в данном случае вид
3(x<n))2 - 1- е-х<п>x<n + 1) =х(п) _ ......__..______
6x(n) + е-х<п> '
приведены в табл. 9.9.
Таблица 9.9
п х/•) lx/•) -х<•- I) 1
о 0.5000000
0.7374944 2· 10-1
2 0.7062126 3. 10-2
3 0.7056421 6. lo-4
4 0.7056419 2 • lo-7
При п =4 итерации прерываются. Можно считать, что х =О.705642 ±
± 10--{;. Заметим, что точность & = 10-2 была достигнута уже после
выполнения двух итераций. .А
3. Метод последовательной параболической интерполяции. Эrот
метод предназначен для минимизации гладких функций, но в отличие от
методов бисекции и Ньютона не требует вычисления производных.
Опишем одну итерацию простейшего варианта этого метода. Пред­
положим, что уже известны три предыдущих приближения x<k - 2), x<k - 1),
x(k) к точке х. Пусть у = Р2(х) = m<k) + п<k>(х - x<k>) +p<k>(x - x<k>)2 -
309

311. Глава 9. Методы одномерной минимизации
уравнение параболы, проходящей через три точки плоскости с коорди­
натами (x(k - 2), J(x<k - 2>)), (x<k - 1>, j(x(k - 1>)), (x<k>, j(x(k>)). Здесь
п(k) = x<k- 1) - x(k) J(x<k>) - f(x<k- 2>) +
x<k- l)_x(k-2) x(k) _x(k-2)
t(k) _ x<k- 2) !(x<k-1 >) _!(x<k>)
+ •x<k-1)_x(k-2) x<k-)_x(k)
1 [fl._x(k- 1>) _!(x<k>) f (x<k>) _/(x<k- 2>)]
p(k)= - .
x<k-l)_x(k-2) x<k-1)_x(k) x<k>-x<k-2)
За очередное приближение x<k + 1) к х принимается та точка, в
которой функция Р2(х) достигает минимума. Из уравнения
P],(x<k + 1>) = 2p(k)(x<k+ 1) - x<k)) + п<kJ = О
получается формула
п<k)
x(k+J=x(k) ___
2p(k).
(9.18)
Естественно, что для начала работы этого метода требуется выбор
трех начальных приближений х<О>, хО), х<2>.
Пусть функция/трижды непрерывно дифференцируема в некоторой
окрестности точки х и удовлетворяет условию f"(x) > О. Можно
показать, что в этом случае выбор начальных приближений х<О>, x(I >, х<2)
из достаточно малой окрестности точки х гарантирует, что p(k) *О для
всех k и метод последовательной параболической интерполяции схо­
дится сверхлинейно, с порядком, приближенно равным 1.324. Поэтому
в качестве критерия окончания итерационного процесса можно
принять неравенство (9.17).
Отметим, что в описанном методе используются только значения
функции f, вычисляемые в точках x<k>. Поэтому (как и для методов
прямого поиска) при его реализации на компьютере достижимая точность
метода ограничена снизу значением, равным радиусу & интервала неоп­
ределенности. После того как очередное приближение х<п> попадет
в интервал (х - &, х + Ё ), дальнейшие вычисления теряют смысл (см.
§ 9.2).
Существуют различные модификации метода последовательной
параболической интерполяции. Одна из них, например обеспечивает
принадлежность очередного приближения предыдущему отрезку лока-
лизации и дает последовательность стягивающихся к точке х отрезков.
310

312. § 9.5. Дополнительные замечания
4. Гибридные алгоритмы. Лучшими среди универсальных
методов одномерной минимизации считаются так называемые гиб­
ридные (или регуляризованные) алгоритмы. Они представляют собой
комбинации надежных, но медленно сходящихся алгоритмов типа
бисекции (если возможно вычисление f'(x)) или золотого сечения с
быстро сходящимися методами типа последовательной параболической
интерполяции или Ньютона. Эти алгоритмы обладают высокой надеж­
ностью и гарантированной сходимостью, причем сходимость стано­
вится сверхлинейной, если в окрестности точки строгого минимума
функция f достаточно гладкая.
Примером эффективного гибридного алгоритма является алгоритм
FMIN, изложенный в [106]. Алгоритм FMIN осуществляет поиск
минимума методом золотого сечения, переключаясь по возможности на
параболическую интерполяцию.
§ 9.5. Допоnнитеnьные замечаниw
1. Дополнительную информацию о методах одномерной миними­
зации можно найти, например в [20].
2. Описанные выше методы приспособлены, как правило, для
минимизации унимодальных функций. Если эти методы применить для
минимизации непрерывной функции, не являющейся унимодальной на
рассматриваемом отрезке, то мы получим, вообще говоря, лишь точку
локального экстремума. Поэтому такие методы часто называют
локальными методами минимизации. К настоящему времени разра­
ботан ряд методов, которые предназначены для поиска глобального
минимума. С некоторыми из них можно ознакомиться в [20].
З. Решение задачи минимизации существенно усложняется, если на
значения функции накладываются случайные ошибки (помехи). Так
бывает, например, тогда, когда значения функции получают в
результате измерений какой-либо физической величины. В том случае,
когда ошибки являются случайными величинами и обладают опреде­
ленными вероятностными характеристиками, для поиска минимума
можно использовать метод стохастической аппроксимации. Понятие
об этом методе можно получить из [20]; там же содержатся ссылки на
соответствующую литературу.
311

313. Глава 10
МЕТОДЫ МНОГОМЕРНОЙ МИНИМИЗАЦИИ
Одной из наиболее часто встречающихся в прикладных расчетах
и научных исследованиях вычислительных задач является задача мини-
мизации 1 функции т действительных переменных f(x1, х2, ., хт).
Функция f (целевая функция) минимизируется на некотором мно­
жестве Х с Rm. В случае, когда Х =Rm (т.е ограничения на переменные
х1 , х2, •.• , хт отсутствуют) принято говорить о задаче безусловной мини-
мизации. В противном случае (т.е. тогда. когда Х cF- Rm) говорят о задаче
условной минимизации.
В данной главе рассматриваются методы решения задачи безус­
ловной минимизации. Многие из них являются основой для перехода к
более сложным методам решения задач условной минимизации.
§ 10.1. Задача безусnовной минимизации функции
многих переменных
1. Постановка задачи. Определения. Пусть f(x) =f(x1, х2, •.• , хm)­
действительная функция многих переменных, определенная на мно­
жестве Х с Rm. Точка х Е Х называется точкой глобального минимума
функции f на множестве Х, если для всех х Е Х выполняется нера­
венство f(x) ::;; f(x). В этом случае значение f(x) называется мини­
мальным значением функции f на Х.
Точка х Е Х называется точкой локального wинимума функции f,
если существует такая сS-окрестность U5 этой точки, что для всех х Е Х5 =
=Xn И5 выполняется неравенство f(x)::;; f(x). Если же для всех х Е Х5
таких, что х cF- х, выполняется строгое неравенство f(x) < f(x), то х
называется точкой строгого локального .wинимума.
Подавляюшее большинство методов решения задачи безусловной
минимизации в действительности являются методами поиска точки
локального минимума. За исключением весьма редких случаев для нахо­
ждения точки глобального минимума, вообще говоря, не остается ничего
иного, как найти все точки локального минимума и, сравнив вычис-
1 Как и в случае одной переменной, задача максимизации сводится к задаче миними­
зации заменой функции/на -/.
312

314. § 10.1. Задача безусловной минимизации функции многих переменных
ленные в этих точках значения функции f, выделить среди них точку
глобального минимума. Однако такой подход связан с чрезмерно
большими вычислительными затратами и вряд ли перспективен. На
практике чаще используется другой подход к нахождению точки гло­
бального минимума, который состоит в том, чтобы определить ее
местоположение из анализа самой решаемой задачи, а затем применить
для вычисления один из методов поиска точки локального минимума.
2. Поверхность уровня, градиент и матрица Гессе. Необходимые
и достаточные условия локального минимума. Напомним некоторые
определения и факты, известные из стандартного курса теории
функций многих переменных.
Множество точек, для которых целевая функция принимает посто­
янное значение f(x) =с, называется поверхностью уровня. В случае т = 2
это множество называют линией уровня. На рис. 10. показано, как
получаются линии уровня для функции двух переменных. Функция
f(x1, х2) задает в трехмерном пространстве некоторую поверхность и=
= f(x 1, х2), низшая точка которой и дает решение задачи миними­
зации. Для того чтобы изобразить рельеф этой поверхности, проведем
несколько равноотстоящих плоскостей и = const. Проекции на плос­
кость Ох 1х2 линий пересечения этих плоскостей с поверхностью и
дают линии уровня.
Для дифференцируемой функции определен вектор из первых
частных производных
- ' -( дf дf дf ~ тg(x)-f (х)- -(х), - (х), .., - (х)) ,
дх, дхz дхт
и
о
Рис. 10.1
313

315. Глава 10. Методы многомерной минимизации
Градиент
g(x<O))
Антиградиент
-g (х10))
Рис. 10.2
который называется градиентом. Если в точке х градиент не равен нулю,
то он, как известно, перпендикулярен проходящей через эту точку
поверхности уровня и указывает в точке х направление наискорейшего
возрастания функции. Вектор -g(x) называется антиградиентом
и указывает направление наискорейшего убывания функции (рис. 10.2).
Известно также, что равенство нулю градиента в точке х является
необходимым условием того, чтобы внутренняя для множества Х точка х
была точкой локального минимума дифференцируемой функции f
Точках, для которой выполняется равенство
f'(x) =О, ( 0.1)
называется стационарной точкой функции f. Равенство (10.1) пред­
ставляет собой систему т нелинейных уравнений относительно ком­
понент х 1 , х2 , "., хт векторах, имеющую вид:
(10.2)
а/
- (х 1 ,х2, ".,хт)=О.
дхт
Однако не всякая стационарная точка является точкой локального
минимума. Пусть функция f дважды непрерывно дифференцируема.
Тогда достаточным условием того, чтобы стационарная точка х была
точкой локального минимума, является положительная определен­
ность 1 матрицы
G(x) =f"(x) = (10.3)
1 Определение положительно определенной симметричной матрицы см. в§ S.3.
314

316. § 10.1. Задача безусловной минимизации функции многих переменных
составленной из вторых частных производных функции f Матрицу
(10.3) принято называть матрицей Гессе 1 •
3. Выпуклые функции. Понятие выпуклости играет значительную
роль в теории методов минимизации. Функция f называется строго
выпуклой, если для любых х *у, О < Л. < 1 выполняется неравенство2
/(Лх + (1 - Л.)у) < Л./(х) + (1 - Л.)/(у).
Это определение имеет наглядный геометрический смысл - график
функции f на интервале, соединяющем точки х и у, лежит строго ниже
хорды, соединяющей точки (х, /(х)) и (у, /(у)) (рис. 10.3). Для дважды
непрерывно дифференцируемой функции положительная определен­
ность матрицы Гессе /"(х) является достаточным условием строгой
выпуклости.
Функция/ называется сильно выпуклой с постоянной х >О, если для
любых х, у, О < Л. < 1 выполнено неравенство2
/(Лх+(l-Л.)у):!>Л./(х)+(l-Л.)/(у)- ~Л.(1-Л.)lх-уl 2 . (10.4)
Дважды непрерывно дифференцируемая функция f является сильно
выпуклой тогда и только тогда, когда для всех х матрица Гессе удовле­
творяет условию
(f'(x)~, ~) ~ xl~l 2 для всех ~ е Rm,
где х >О - постоянная, входящая в неравенство (10.4).
и
Рис. 10.3
1Людвиг Отrо Гессе (1811-1874)- иемецкиil математик.
2всюдувэтойглаве lxl=llxll 2 = Jrix.(••1
315

317. Глава 10. Методы многомерной минимизации
4. Задача минимизации квадратичной функции. Часто первона­
чальное исследование свойств методов безусловной минимизации про­
водится применительно к задаче минимизации квадратичной функции
1 т т т
F(х 1 ,х2,".,хт)=2 L La11x1x1-Lb1x1, (10.5)
1=1 1=1 1=1
коэффициенты 0 11 которой являются элементами симметричной поло­
жительно определенной матрицы А. Использовав матричные обозна­
чения, запишем функцию F так:
1
F(x) = 2(Ах, х) - (Ь, х). (10.6)
Вычислим градиент и матрицу Гессе для функции (10.5). Дифферен­
цирование F по xk дает
дF 1 т 1 т
fu = 2 L 0k1x1+2 L 01tx1-bk.
k 1=1 1=1
Пользуясь симметрией матрицы А, получаем формулу
Таким образом.
дF т
дхk = Lak1x1 -bk, 1 5, k 5, т.
1=1
F'(x) =Ах - Ь.
(10.7)
(10.8)
д 2 F
Дифференцируя обе части равенства ( 1О.7) по х1, получаем - - =
ax,axk
= a1k. Это означает, что для квадратичной функции ( 0.5) матрица Гессе
не зависит от х и равна А.
Задача минимизации квадратичной функции представляет интерес
по многим причинам. Отметим две основные из них. Во-первых, в
малой окрестности точки минимума х гладкая целевая функция
хорошо аппроксимируется суммой первых трех слагаемых ее разло­
жения по формуле Тейлора:
f(x) :.: F. (х) = f(x0
) + (g(x" ), х - х") + ~ (G(x")(x - х• ), х -х") (10.9)
с центром в точке х• :.: х .Функция F. с точностью до постоянного сла­
гаемого может быть записана в виде (10.6) с матрицей А = G(x") :.:
:.: G(x). Поэтому можно ожидать, что вблизи точки минимума качест­
венный характер поведения последовательности х<п>, генерируемой
316

318. § 10.1. Задача безусловной минимизации функции многих переменных
методом минимизации, для функции f окажется почти таким же, как
и для квадратичной функции F.
Во-вторых, хорошо известно, что когда А - симметричная положи­
тельно определенная матрица, задача минимизации квадратичной
функции (10.6) эквивалентна задаче решения системы линейных алгеб­
раических уравнений
Ах=Ь. (10.IO)
Более того, решение х0 системы (10.1О) дает точку минимума
функции (10.6). Действительно, F'(x0) = Ах0 - Ь = О, т.е. хо является ста­
ционарной точкой функции F. Так как матрица Гессе F"(x0) = А поло­
жительно определена, то в точке х0 выполнены достаточные условия
минимума и, значит, хО = х .
Таким образом, всякий метод безусловной минимизации, будучи
примененным к поиску минимума функции (10.6), порождает неко­
торый метод решения системы (10.1 О).
Отметим, что поверхностями уровня квадратичной функции (10.6)
служат т-мерные эллипсоиды (при т = 2 - эллипсы) с центром в точке
х. Отношение большей оси каждого из этих эллипсоидов (эллипсов) к
меньшей оси равно сопd 2(А) = Л.mах/Л.mш - числу обусловленности
матрицы А. Здесь Л.mах и Л.mш - максимальное и минимальное собст­
венные значения матрицы А. Чем больше отношение Лmах/Л.mш• тем
сильнее вытянуты поверхности (линии) уровня.
5. Обусловленность задачи минимизации. В § 9.2 достаточно
подробно обсуждалась обусловленность задачи поиска строгого
локального минимума функции одной переменной. Так как ситуация
в многомерном случае аналогична, то здесь изложим соответствующие
положения более кратко.
Пусть х - точка строго локального минимума дважды непрерывно
дифференцируемой функции/, матрица Гессе которой в точке х поло­
жительно определена. Предположим, что в некоторой окрестности
точки минимума вычисляемые приближенные значения /•(х) удовле-
творяют неравенству lf(x)-/'(x)I ~ Л=Л(f*). Тогда для радиуса
соответствуюшей области неопределенности справедлива грубая
оценка Е "" 2JЛ;л.m•n, где Л.mш >О - минимальное собственное зна­
чение матрицы Гессе f"(x).
317

319. Глава 10. Методы многомерной минимизации
Отсюда следует, что методы приближенного решения задачи мини­
мизации, в которых используются только значения 1", не могут, вообще
говоря, гарантировать получение приближенного решения х• с
погрешностью меньшей чем Л(х")"" 2JЛ11"m•n. Это означает,
например, что даже для хорошо масштабированных задач (т.е. при
1х1 - 1, lf(х) 1 - 1, Л.m•n - 1) неизбежна потеря примерно половины из
того числа верных значащих цифр, которые содержались в прибли­
женных значениях 1"(х).
Пусть теперь для решения задачи минимизации доступны прибли­
женные значения градиента (/1)
0
• Тогда сведение задачи поиска точки
минимума х к эквивалентной задаче решения системы уравнений f'(x) = О
существенно улучшает обусловленность задачи. В частности, спра­
ведлива такая оценка границы абсолютной погрешности:
Л(х*)"" - 1- Л((f')").
лmш
Здесь Li((f')*) граница абсолютной погрешности значений (/')0
,
считающаяся достаточно малой величиной. Поэтому если для вычис-
-
ления х можно использовать значения градиента, то такой возмож-
ностью не следует пренебрегать.
§ 10.2. Пон1тие о методах спуска.
Покоординатный спуск
1. Методы спуска. Большинство итерационных методов, приме­
няемых для решения задачи безусловной минимизации функций
многих переменных, относятся к классу методов спуска, т.е. таких
методов, для которых каждая итерация (шаг) приводит к уменьшению
значения целевой функции: J(х<п + 1>) < J(x<n>) для всех п ~О.
Опишем структуру типичной (п + 1)-й итерации метода спуска
в предположении, что приближение х<п> к точке минимума уже
найдено и х<пJ * х .
1°. Находят ненулевой вектор р<п>, называемый направлениеw
спуска. Этот вектор должен быть таким, чтобы при всех достаточно
малых а > О выполнялось неравенство
j(х<п> + ap<n>) < f(x<n>). (10.ll)
318

320. § 10.2. Понятие о методах спуска. Покоординатный спуск
Если ввести функцию одной переменной а, имеющую вид
<рп (а) = f(_x(n) + ap(n) ),
то неравенство (10.11) можно записать так: <рп(а) < <рп(О).
(10.12)
2°. Вычисляют положительное число ап (шаг спуска), для которого
выполняется неравенство
f(x(n) + anp<n>) < J(x<n>),
или, что то же самое, неравенство <рп(ап) < <рп(О).
(10.13)
3°. За очередное приближение к точке минимума принимают
х<п + 1) =х(п) + апр(п).
4°. Проверяют выполнение критерия окончания итераций. Если кри­
терий выполняется, то итерации прекращают и полагают х ""х<п + 1J.
В противном случае итерации продолжают далее.
Последовательность точек х0, х 1, ••• , х<п), ..., генерируемую методом
спуска, иногда называют траекторией спуска.
2. Направление спуска. Заметим, что вектор р<п) не может быть
задан произвольно. В силу требования (10.11) функция <рп(а), опреде-
ляемая формулой (10.12), должна убывать в точке а = О. Для того чтобы
это условие выполнялось, достаточно потребовать выполнения нера­
венства <р~(О) < О. Так как <р~( а) = (f'(х<п> + ap<n)),p<n>), то вектор р<п>
является направлением спуска, т.е. удовлетворяет условию (10.11), если
(10.14)
Можно показать, что для строго выпуклой функции f это нера­
венство выполняется тогда и только тогда, когда вектор р<п> задает
направление спуска.
Обычно именно способ выбора направления спуска р<п> определяет
конкретный численный метод, а различные варианты метода опреде­
ляются далее алгоритмом вычисления шага спуска ап. Например,
выбор в качестве р<пJ антиградиента р<п) = -/'(х<")) задает градиентный
метод (см.§ 10.3). В этом случае (f'(x<n>), р<п>) = -l/'(x<n>)l 2 <О, т.е.
условие (10.14) выполняется.
3. Выбор шага спуска. Следует иметь в виду, что шаг ап спуска
определяет «истинную>> величину шага hn = lx<n + 1> -х<п> 1= ап jp<nJ 1. но
совпадает с ней только тогда, когда вектор р<п) имеет единичную длину.
319

321. Глава 10. Методы многомерной минимизации
В качестве ап можно выбирать значение параметра а, которое обес­
печивает достижение наименьшего значения функции/ вдоль луча х =
=х<п> + ар<п>, а <:: О. В этом случае для вычисления ап требуется
решение одномерной задачи минимизации функции <рп(а). Этот путь
достаточно надежен, однако может быть связан с большими вычисли­
тельными затратами.
Существуют и активно применяются другие подходы к выбору ап,
гарантирующие выполнение условия (10.13). Один из простейших под­
ходов, называемый дроблением шага, состоит в следующем. Фик­
сируют начальное значение шага а и выбирают параметр у, О < у < 1
(часто у= 1/2). За шаг спуска принимают ап =а /п, где in - первый из
номеров 1 = О, 1, 2, ..., для которого выполнено условие
f(x(n) +а у•р(п)) - f(x(n)) ~ рау1 (/'(х<п>),р<п>). (10.15)
здесь О < р < 1, р - некоторый дополнительный параметр.
4. Критерии окончания итераций. На практике часто используют
следующие критерии окончания итераций:
lx(n+l)_x(n)I <i;1, (10.16)
1/(х<п _,_ 1)) - J(х<п)) 1 < Е2, (10.17)
l/'(x<п>)i < Е3, (10.18)
где Ер Е2, i;3 - заданные положительные числа. Нередко используют раз­
личные их сочетания, например требуют, чтобы одновременно выпол­
нялись условия (l0.16) и (l0.17) или даже все три условия (10.l6Hl0.18).
Нередко вместо критериев (10.16), (10.17) применяют их аналоги,
основанные на сочетании понятий относительной и абсолютной
погрешностей:
lx(n+l)_x(n)I <Б1(1 + lx(n+l)I),
lf(x(n + 1)) - /(х<п>) 1 < Б2(1 + 1j(х<п + 1))1),
а также другие критерии.
(10.19)
(10.20)
К сожалению, надежные критерии окончания счета, которые были
бы применимы к широкому классу задач и гарантировали бы дости­
жение нужной точности, пока не известны.
5. Покоордииатный спуск. В методе покоординатного спуска в
качестве очередного направления спуска выбирают направление
одной из координатных осей. Наиболее известным является метод
циклического покоординатного спуска. Опишем очередной (п + 1)-й
цикл одного из вариантов этого метода, в предположении, что прибли­
жение х<п> уже найдено.
320

322. § 10.2. Понятие о методах спуска. Покоординатный спуск
Цикл с номером п + 1 состоит из т шагов. На первом шаге произ-
3 _ (п) _ (п)
водят спуск по координате х 1• начения х2 - х2 , .•• , хт - хт
(п + 1)
остальных координат фиксируют, а х 1 выбирают из условия
(п+ 1) (n) (п) _ . (п) (п)
f(x 1 ,х2 , .••,хт )-mш/(х 1 ,х2 , ••• ,хт ).
xl
Фактически решается задача минимизации функции одной переменной
f (п) (п)
/1 (х 1 ) = (х 1 ,х2 , .•• ,хт ).
На втором шаге производят спуск по координате х2• Значения х1 =
(п + 1) (n) (n) ф
= х 1 , х3 = х3 , ••• , хт = хт остальных координат иксируют
(n+I) б v
и х 2 вы ирают как решение задачи одномернои минимизации
(п + 1) (п + 1) (п) (n) _ J (п + 1) (п) (n)
f(x 1 ,х2 ,х3 , •.• ,хт )-mш (х 1 ,х2,х3 , ••• ,хт ).
х2
Аналогично осуществляют остальные шаги. На последнем т-м шаге
(п + 1)
координату хт определяют из условия
(п+ 1) (п+ 1) (п+ 1) _ (п+ ) (п+ 1)
f(x 1 , ...,xm-I ,хт )-mш/(х 1 , ••• ,xm-I ,хт).
хт
В результате получается очередное приближение х<п + 1) к точке
минимума. Далее цикл метода снова повторяют.
На рис. 10.4 изображена геометрическая иллюстрация циклического
покоординатного спуска.
о
Рис. 10.4
321

323. Глава 10. Методы многомерной минимизации
Применим метод циклического покоординатного спуска для мини­
мизации квадратичной функции (10.5). Так как на k-м шаге очередного
(п + 1)
цикла значение координаты xk определяется из условия миними-
зации функции F по направлению xk, то необходимо, чтобы в точке
(n+ 1) (n+ 1) (n+ 1) (n) (n) дF/д
(х 1 , • ", xk- 1 , xk , xk +1, •••, хт ) производная xk обра-
щалась в нуль. Учитывая формулу ( 1О.7), получаем уравнение
k т
Lak1x}n+I)+ L akJxjn>-bk=O,
1= 1=k+ 1
откуда находим
(n+I) -( k-I (n+I) т (n)
xk = akk bk - L ak1x1 - L ak1x1 ) . (10.21)
1=1 1=k+I
Последовательные вычисления по формуле (10.21) для k = 1, 2, ..., т
и составляют один цикл метода покоординатного спуска. Заметим, что
этот метод применительно к решению системы линейных алгебраи­
ческих уравнений Ах = Ь с симметричной положительно определенной
матрицей дает известный итерационный метод Зейделя (см. гл. 6), схо-
дящийся со скоростью геометрической прогрессии.
§ 10.3. Градиентный метод
Рассмотрим задачу безусловной минимизации дифференцируемой
функции многих переменных f(x). Пусть х<п> - приближение к точке
минимума х, а g<п> = g(x<n>) - значение градиента в точке х<п>. Выше
уже отмечалось, что в малой окрестности точкихfn) направление наиско­
рейшего убывания функции f задается антиградиентом - g<п>. Это
свойство существенно используется в ряде методов минимизации.
В рассматриваемом ниже градиентном методе за направление спуска
из точки х<п> непосредственно выбирается p<nJ = - g<п>. Таким образом,
согласно градиентному методу
х<п + 1) =x(n) - апg<п>. (10.22)
Существуют различные способы выбора шага ап, каждый из
которых задает определенный вариант градиентного метода.
1. Метод наискорейшего спуска. Рассмотрим функцию q>n(a)
= f(х<п> - ag<n>) одной скалярной переменной а ~ О и выберем в
качестве ап то значение, для которого выполняется равенство
(10.23)
322

324. § 10.3. Градиентный метод
Рис. 10.S
Этот метод, предложенный в 1845 г. О. Коши 1, принято теперь
называть методом наискорейшею спуска.
На рис. 10.5 изображена геометрическая иллюстрация этого метода
для минимизации функции двух переменных. Из начальной точки х<0>
перпендикулярно линии уровня f(x) = f(x<O>) в направлениир<0> = -g<0>
спуск продолжают до тех пор, пока не будет достигнуто минимальное
вдоль лучах<0> + ар<0> (а> О) значение функции/ В найденной точке х< 1 >
этот луч касается линии уровня f(x) = f(x(I>). Затем из точки х< 1 > про­
водят спуск в перпендикулярном линии уровня направлении р< 1 > = -gO>
до тех пор, пока соответствующий луч не коснется в точке х(2), прохо­
дящей через эту точку линии уровня, и т.д.
Отметим, что на каждой итерации выбор шага ап предполагает
решение задачи одномерной минимизации (10.23). Иногда эту операцию
удается выполнить аналитически, например для квадратичной функции.
Применим метод наискорейшего спуска для минимизации квадра­
тичной функции
1
F(x) = 2 (Ах, х) - (Ь, х) (10.24)
с симметричной положительно определенной матрицей А.
Согласно формуле (10.8), в этом случае g<п> = А.х(п) - Ь. Поэтому
формула (10.22) выглядит здесь так:
х<п + l) =х<пJ - ап(А.х(п) - Ь). (10.25)
Заметим, что
1
<рп(а) = 2 (А(х<п> - аg<п>), х<пJ - аg<п>) - (Ь, х<п> - аg<п>) =
1 1
= 2 (Ag<n>, g<nJ)a2 _ (g(п), g(n)) а + 2 (А.х<п>, х<п>) _ (Ь, х<п>).
1 Оrюстен Лун Коши (1789-1857) - франuузскнй математик, один из создателей
современного математического анализа, теории дифференциальных уравнений и др.
323

325. Глава 10. Методы многомерной минимизации
Эта функция является квадратичной функцией параметра а и достигает
минимума при таком значении а = а", для которого
q>~(an) = (Ag<n>, g("!)a" - (g<п>, g(n)) = О.
Таким образом, применительно к минимизации квадратичной
функции (10.24) метод наискорейшего спуска эквивалентен расчету по
формуле (10.25), где
(g(п), g<">)
а =п (Ag(n), g(n>) ·
(10.26)
Замечание 1. Поскольку точка минимума функции (10.24)
совпадает с решением системы Ах = Ь, метод наискорейшего
спуска (10.25), (10.26) может применяться и как итерационный
метод решения систем линейных алгебраических уравнений с сим­
метричными положительно определенными матрицами (см. § 6.4,
пункт 8). При этом g(n) = -r <п>, где r (п) = Ь -Ax<n) - невязка, отве­
чающая приближению x<n>.
Замечание 2. Отметим, что а~1 = p(g<">), где р(х) =
= (Ах, х)/(х, х) - отношение Рэлея (см. § 8.1 ).
Пример 10.1. Применим метод наискорейшего спуска для мини­
мизации квадратичной функции f(x 1, х2) = х7 + 2х; - 4х1 - 4х2 .
Заметим, что f(x1, х2) = (х 1 - 2)2 + 2(х2 - 1)2 - 6. Поэтому точное зна­
чение х = (2, 1)Т точки минимума нам заранее известно. Запишем данную
функцию в виде (10.24), где матрица А = [~ ~ и вектор Ь = (4, 4)7: Как
нетрудно видеть, А= Ат> О.
Возьмем начальное приближение х(О) = (О, О)Т и будем вести вычис­
ления по формулам (10.25), (10.26).
1-я итерация.
( (О) (0)) 42 + 4'
g(O)=Ax(O)_b=(-4 -4)Т а= g ,g -
, , О (Ag(O), g(O)) 2. 42 + 4. 42 - J'
( 4 4)Тx(I) =х(О) - а~и<О) = - -U<> 3'3.
2-я итерация.
(l>=Ax(IJ_ь=(-~ ~)та= (g(l),g(I>) = (4/3)2+(4/3)2 =~
g 3'3 ' 1 (AgOJ,g(I)) 2·(4/3)2+4·(4/3)2 3'
324

326. § 10.З. Градиентный метод
( 16 8)Тх(2) =x(I) - а g(I) = - -
1 9, 9
Можно показать, что для всех п ;;:: 1 на п-й итерации будут получены
значения
g<п)= ~: (1,(-l)")r, ап=j, х<п)=х-~ (2,(-l)n)r.
Заметим, что Jх<п) _ х 1 = J5 --> О при п--. оо. Таким образом, после-3п
довательность х<пJ, полученная методом наискорейшего спуска, сходится
со скоростью геометрической прогрессии, знаменатель которой q = 1/3.
На рис. 10.5 изображена именно та траектория спуска, которая была
получена в данном примере. .&
Для случая минимизации квадратичной функции справедлив сле­
дующий общий результат [20].
Теорема 10.1. Пусть А - симметричная положительно опреде­
ленная матрица и минимизируется квадратичная функция (10.24). Тогда
при любом выборе начального приближения метод наискорейшего спуска
(10.25), (10.26) сходится и верна СТ/едующая оценка погрешности:
Jx<п>-xJ::;; Jcond2(A) qn Jx<0>-xl (10.27)
cond2(A) - 1 Л.mах
Здесь q = d (А)+ 1 < 1, где cond2(A) = ,-- , а "-mш и "-max - мини-
соn 2 ""mш
мальное и максимальное собственные значения матрицы А. 8
Отметим что этот метод сходится со скоростью геометрической
прогрессии, знаменатель которой равен q. Если "-mш и Лmах близки, то
cond2(A) - 1 и q мало. В этой ситуации метод сходится достаточно
быстро. Например, в примере 10.1 имеем "-mш = 2, "-max = 4 и поэтому
cond2(A) = 2, q = (2 - 1)/(2 + 1) = 1/3. Если же "-mш « "-max' то
condiA) » 1, q "" 1 и следует ожидать медленной сходимости метода
наискорейшего спуска.
Пр и мер 10.2. Применение метода наискорейшего спуска для
минимизации квадратичной функции /(х1, х2) = х7 + lOx;- 4х1 -4х2
при начальном приближениих<0> =(О, О)т дает последовательность при­
ближений х<п> = x-2(9/1)n(l,(-l)п)r, где х = (2, 0.2)r. Траектория
спуска изображена на рис. 10.6.
325

327. Глава 10. Методы многомерной минимизации
• х
Рис. 10.6
Последовательностьх(п) сходится здесь со скоростью геометрической
прогрессии, знаменатель которой равен q = 9/1 1, т.е. существенно мед-
леннее, чем в примере 10.1. Так как здесь А = r2 О J, тоЛmш = 2, Лmах =
lo 20
=20, cond2(A) = 20/2 = 10, q = (10 - 1)/(10 + 1) = 9/11, и полученный
результат вполне согласуется с оценкой (10.27). •
Замечание 1 Мы сформулировали теорему о сходимости
метода наискорейшего спуска в предположении, что целевая функ­
ция является квадратичной. В общем случае, если минимизируе-
мая функция строго выпуклая и имеет точку минимума х , то
также независимо от выбора начального приближения полученная
указанным методом последовательностьх(n) сходится к х при п-+ оо.
При этом после попадания x(n) в достаточно малую окрестность
точки минимума сходимость становится линейной и знаменатель
соответствующей геометрической прогрессии оценивается сверху
~ - х - 1 Л.mах
величинои q :::: -+i , где х = :;--- - отношение максимального
Х лmш
и минимального собственных значений матрицы Гессе G( х ), т.е.
х = condi G(x )).
Замечание 2. Для квадратичной целевой функции (10.24)
решение задачи одномерной минимизации (10.23) удается найти
в виде простой явной формулы (10.26). Однако для большинства
других нелинейных функций этого сделать нельзя и для вычисле­
ния ап методом наискорейшего спуска приходится применять чис-
ленные методы одномерной минимизации типа тех, которые были
рассмотрены в гл. 9.
2. Проблема «Оврагов». Из проведенного выше обсуждения следует,
что градиентный метод сходится достаточно быстро, если для минимизи­
руемой функции поверхности уровня близки к сферам (при т = 2 линии
326

328. § 10.3. Градиентный метод
уровня близки к окружностям). Для таких функций х = Лmах/Л.mш "" 1.
Теорема !0.1, замечание 1, а таюке результат примера 10.2 указывают на то,
что скорость сходимости резко падает при увеличении величины х. Дейст­
вительно, известно, что градиентный метод сходится очень медленно, если
поверхности уровня минимизируемой функции сильно вытянуты в неко­
торых направлениях. В двумерном случае рельеф соответствующей
поверхности и = f(x1, х2) напоминает рельеф местности с оврагом
(рис. 10.7). Поэтому такие функции принято называть овражными. Вдоль
направлений, характеризующих «дно оврага», овражная функция меняется
незначительно, а в других направлениях, характеризующих «склон оврага)),
происходит резкое изменение функции.
Если начальная точка х<0> попадает на «склон оврага)), то направление
градиентного спуска оказывается почти перпендикулярным «дну оврага))
и очередное приближение x{I) попадает на противоположный «склон
оврага)). Следующий шаг в направлении ко «дну оврага)) возвращает при­
ближение х<2> на первоначальный «склон оврага)). В результате вместо
того чтобы двигаться вдоль «дна оврага)) в направлении к точке
минимума, траектория спуска совершает зигзагообразные скачки поперек
«Оврага)), почти не приближаясь к цели (рис. 1О.7).
Для ускорения сходимости градиентного метода при минимизации
овражных функций разработан ряд специальных «Овражных)) методов.
Дадим представление об одном из простейших приемов. Из двух близких
начальных точек z(O) и z(l) совершают градиентный спуск на «дно
оврага)). Через найденные точки х<0> и x<l) проводят прямую, вдоль
которой совершают большой «овражный)) шаг (рис. 10.8). Из найденной
таким образом точки z<2> снова делают один шаг градиентного спуска
в точку х<2>. Затем совершают второй «овражный)) шаг вдоль прямой,
проходящей через точки хО> и х(2), и т.д. В результате движение вдоль
«дна оврага)) к точке минимума существенно ускоряется.
hc.10.7
327

329. Глава 10. Методы многомерной минимизации
Рис. 10.8
Более подробную информацию о проблеме <<Оврагов» и «Овражных»
методах можно найти, например в (9, 20].
3. Другие подходы к определению шага спуска. Как нетрудно
понять, на каждой итерации было бы желательно выбирать направ­
ление спуска р <11>, близкое к тому направлению, перемещение вдоль
которого приводит из точких<11> в точку х. К сожалению, антиградиент
р<11> =-g<11>является, как правило, неудачным направлением спуска. Осо­
бенно ярко это проявляется для овражных функций. Поэтому возникает
сомнение в целесообразности тщательного поиска решения задачи
одномерной минимизации (10.23) и появляется желание сделать в
направлении р<11> лишь такой шаг, который бы обеспечил «сущест­
венное убывание» функции f Более того, на практике иногда довольст­
вуются определением значения а" > О, которое просто обеспечивает
уменьшение значения целевой функции.
В одном из простейших алгоритмов (типа дробления шага) такого
выбора шага а11 фиксируют начальное значение а > О и значение пара-
метра у, О < у < 1. За а11 принимают а11 = а · у'п, где 111 - первый из
номеров 1 = О, 1, 2, "" для которого выполнено условие убывания
j(x<11> - ау 1g<п>)- J(x<11>) <О. (10.28)
Однако при таком выборе а" нет гарантии, что последовательность
х<11> будет сходиться к точке минимума даже для простой квадратичной
функции (10.24). Условие (10.28) является слишком слабым: последова­
тельность х<11>, незначительно уменьшая значения функции /, может
«останавливаться», не доходя до точки х .Такое поведение последова-
328

330. § 10.3. Градиентный метод
тельности х<п> можно предотвратить, если заменить условие (10.28)
условием «существенного убывания» функции f на каждой итерации:
(10.29)
Здесь ~ (О < ~ < 1) - дополнительный параметр.
Заметим, что для рассматриваемого градиентного методар(п) =-g<п> =
= -f'(х<п>) и поэтому неравенство (10.29) в точности совпадает с нера­
венством (10.15), используемым в методах спуска при дроблении шага.
Пр им ер 10.3. Продемонстрируем применение градиентного
метода с дроблением шага к задаче минимизации квадратичной
2 2
функции /(х1, х2) = х1 + 2х2 - 4х 1 - 4х2 из примера 10.1. Для выбора
значения шага будем использовать условие (10.29). Воспользуемся сле­
дующими краткими обозначениями: а, = ау', х<п. 1> = х<п> - а,g<п>.
Заметим, что g(n) = (2хп) - 4, 4х~п) - 4)т.
Выберем начальное приближение х<п> = (О, О)Т, начальное значение
шага а = а0 = 1, значения параметров у = 1/2, ~ = 314. Вычислим зна-
чения J(x<0>) =О, g<0>= (-4, -4)7:
1- я итерация. Вычисляем х(О, О) =х<О> - а~(О) = (4, 4)Т, f(x(O, OJ) =
= 16. Так как значение функции не уменьшилось, то следует уменьшить
шаг: а 1 = а0/2 = 0.5.
Вычисляем x(O,I) = х<0> - a 1g<0> = (2, 2)т, f(x<0• 1>) =-4. Поскольку
J(x<O. 1)) - J(x<O>) = -4 > -~а 1 lg{O)l2 = -12, условие (10.29) не выпол­
няется и следует снова уменьшить шаг: а2 = а/2 = 0.25.
Вычисляем х<0• 2>=х<0> - a 2g<0>= (1, 1) f(x<0• 2>) = -5. Имеем j(x<0• 2>) -
- f(x<0>) =-5 > -~a2 ig<0>1 2 = -6, т.е. условие (10.29) не выполняется.
Уменьшаем шаг: а3 = а2 12 = 0.125.
Вычисляем х<о. З) =х<О> - a3g<0> = (0.5, О.5)т, f(x<0• 3>) = -3.25. Так как
j(x<0• 3))- J(x<0>) = -3.25 < -~a3 lg<0>1 2 = -3, то условие (10.29) выполнено.
Положим х< 1 > = (0.5, О.5)т; напомним, что J(xO>) = -3.25. Вычислим
g<'> = (-3, -2)т и положим а0 = 1.
Далее вычисления следует продолжить до выполнения какого-либо
принятого критерия окончания итераций. А
4. Влияние погрешности вычислений. Один из сушественных
недостатков градиентного метода связан с его чувствительностью к
погрешностям вычислений. Особенно сильно этот недостаток сказы-
329

331. Глава 10. Методы многомерной минимизации
вается в малой окрестности точки минимума, где антиградиент,
задающий направление поиска, мал по модулю. Поэтому эффектив­
ность градиентного метода на завершающей стадии поиска сущест­
венно ниже, чем на начальной стадии.
§ 10.4. Метод Ньютона
1. Простейший вариант метода Ньютона и метод Ньютона
с дроблением шага. Пусть в некоторой окрестности точки минимума
х функция f является сильно выпуклой и дважды непрерывно диффе­
ренцируемой. Далее, пусть x(n) - хорошее приближение к х . Тогда
в малой окрестности точки х<п> функция f достаточно точно аппрокси­
мируется квадратичной функцией
1
Fn(x) = J(x<11>) +(g(n), х -х<п)) + 2(G(n)(x -х<п>), х -х<п>),
являющейся суммой первых трех членов ее разложения по формуле
Тейлора (ер. с формулой (10.9)). Здесьg<п) = f'(x<11>), G(п) = f"(x<n>).
Можно ожидать, что точка х<п>, в которой достигается минимум
функции Fn, будет значительно лучшим приближением к х, чем х<п).
Учитывая, что F~(x) = g<п> + G<11>(x - х<11>), замечаем, что точка х<п>
может быть определена из необходимого условия экстремума:
g<п> + G<п>(х<п> -х<">) =О.
Таким образом, чтобы попасть из точки х<п> в точку х<п>, нужно
переместиться вдоль векторар(п) = х<п> -х<п>, который определяется из
системы линейных алгебраических уравнений
G(n)p(n) = -g(n), (10.30)
Вектор р (п) принято называть ньютоновским направлением, а метод
спуска
(10.31)
с таким выбором p(n) - методом Ньютона.
Отметим, что ньютоновское направление является направлением
спуска. В самом деле, в силу равенства (10.30) для р<п) верна формула
p(n) = -[G<n)J-lg(n). Матрица [G<11 JJ-I положительно определена (это
следует из положительной определенности матрицы G(")). Поэтому
(f'(x<n>), р<">) = -([G<п>]-lg<п>, g<">) <О.
330

332. § 10.4. Метод Ньютона
Таким образом, условие (10.14) выполняется и р (п) действительно
задает направление спуска.
Различные варианты метода (10.31 ), (10.30) связаны с различными
способами выбора шагов ап. Заметим, что при выборе ап = 1 рассмат­
риваемый метод в точности совпадает с методом Ньютона решения
систем нелинейных уравнений, примененным к решению системы
f'(x) = О. Отсюда - и название метода.
Простым следствием теоремы 7.3 о сходимости метода Ньютона
решения систем нелинейных уравнений является следующая теорема.
Теорема 10.2. Пусть в некоторой окрестности И точки
минимума х функция f является сильно выпуклой и трижды непре­
рывно дифференцируемой Тогда найдется такая малая о-окрест­
ность точки х , что при произвольном выборе начального прибли­
женuя х(О) из этой окрестности последовательностьх(п), вычисляемая
с помощью метода (10.30), (10.31) при а п = 1, не выходит за пределы
о-окрестности точки х и сходится к ней квадратично. •
Замечание. Квадратичная скорость сходимости метода позво­
ляет использовать простой практический критерий окончания:
ix<n+l)_x(n)I <е. (10.32)
Теорема 10.2 указывает на то, что метод Ньютона сходится очень
быстро, и практика вычислений это подтверждает. Однако сущест­
венным недостатком рассмотренного варианта метода является необхо­
димость выбора достаточно хорошего начального приближения,
которое на начальной стадии поиска точки минимума, как правило,
отсутствует. Поэтому метод Ньютона с выбором ап = 1 чаще при-
меняют на завершающем этапе поиска х , когда с помощью других
методов уже найдено достаточно точное приближение к точке
минимума.
Указанного недостатка в значительной степени лишен вариант метода
1
Ньютона, в котором в качестве шага спуска выбирается ап = у п, где 1п -
первый среди номеров 1 ~ О, для которых выполняется неравенство
f(x(n) + у 'р(")) - f(x<">) 5: ~у' (g<п>, Р (n)).
Здесь О< у< 1, О< ~ < 1/2 - параметры метода. Метод Ньютона с
таким выбором ап для широкого класса функций сходится при любом
выборе начального приближения х<О) е И и этим выгодно отличается от
метода с выбором ап = 1.
331

333. Глава 10. Методы многомерной минимизации
Теорема 10.3. Пусть трижды непрерывно дифференцируемая в Rm
функция f имеет точку мини...,ума х и ее матрица Гессе f"(x) положи­
тельно определена. Тогда при любом начальном приближении х(О) после-
довательность х(п), вычисляемая методом Ньютона с выбором ап = у'п,
сходится к х с квадратичной скоростью Более того, найдется номер
п 0 такой, что для всех п ~ п 0 выполняется равенство ап = 1. 8
Заме чан и е Используют и другие способы выбора ап. Напри­
мер, иногда ап выбирают из условия <рп(ап) = mш <рп(а), где
OSetSI
<f>п(а) = /(х(п) + ap(n>).
Квадратичная скорость сходимости метода Ньютона, а также
возможность использования матрицы Гессе для контроля за
соблюдением достаточных условий экстремума делают этот
метод чрезвычайно привлекательным при решении задачи безус­
ловной минимизации.
Пример 10.4. Применим метод Ньютона (10 30), (10.31) сап= 1
для поиска точки минимума функции f(x 1, х2) = х~ + IO(x2 - sinx1) 2
с точностью в = 10-5. Будем использовать критерий окончания ите­
раций (10.32) и вести вычисления на 6-разрядиом десятичном компь­
ютере Отметим, что минимальное и равное нулю значение функция f
достигает в точке х = (О, O)r.
Имеем:
g(n) = f'(x~n>, Х~п» =
= (2х(п) + 20 (sin х(п) - х(п)) • cos х(п) 20(х(п) - sinx(n) ))Т
1 1 2 1 , 2 1 •
[
2 20 2 (п) (п) . (п)
G(n) = f"(x(n>) = + (cos х 1 + х2 • sшх 1 )
20cosx(n)- 1
-20cosx~n~ .
20 J
Возьмем за начальное приближение х(О) = ( 1, 1)Т
1-я итерация. Вычислим
332
g(O) = [0.286928l ,
3.17058 .J
G (О)= [ 10.5065 -10.8060l .
-10.8060 20 J

334. § 10.4. Метод Ньютона
Таблица 10.1
п
(11)
Х1
(n)
Х2 lx<•) -х<•-1)1
о 1.00000000 1.00000000
1 0.57155400 0,60997200 6· 10-1
2 0.15541900 0.1909440 6. 10-1
3 0.00824200 0.00939200 2·10-1
4 0.00000082 0.00000101 1. 10-2
5 0.00000000 0.00000922 2·10~
Таким образом, при п =О система (10.30) принимает следующий вид:
10.5065рО) - 10.8060р~О) = -0286928,
= -3.17058.
Решая ее, получаем р0) = -0.428445, р~О) = -0.390018. Далее в соответ­
ствии с формулой (10.31) полагаем х1 > =х~О) +р0) = 0.571555,
х~1 )=х~0>+р~О) =О.609982. Так как /х< 1 J-х<0>/ ::::0.6>е,товычисления
следует продолжить далее.
Результаты следующих итераций приведены в табл. 10.1.
При п = 5 критерий окончания выполняется и вычисления следует
прекратить. Итак, х ""(0.00000, 0.00000)7: А
2. Понятие о квазиньютоновских методах. Высокая скорость схо­
димости метода Ньютона связана с тем, что в нем используется матрица
Гессе, содержащая информацию о кривизнах функции f. В результате
минимизируемую функцию удается достаточно точно аппроксимировать
последовательностью квадратичных функций Fn. В методах, которые
называют квазиньютоновскими 1, также фактически используется квадра­
тичная аппроксимация функции/, но в отличие от метода Ньютона в них
не применяется вычисление вторых производных. Информация о кри­
визнах функции f здесь накапливается постепенно и является резуль­
татом наблюдений за изменением градиента g<nJ.
1 Первоначально эти методы называли методами переменной метрики.
333

335. Глава 10. Методы многомерной минимизации
Направление спуска в квазиньютоновских методах определяется как
решение системы уравнений
в<п)p(n) = -g<п>,
в которой В <11> - текущее приближение к матрице Гессе. Начальное
приближение в<0> обычно полагают равным единичной матрице. В
таком случае р<0> = -g<0> и первая итерация совпадает с одним шагом
градиентного метода.
После того, как найдено приближение х<п + 1>, вычисляют матрицу
в<п + IJ = в<п> + лв<11>, где лв<11> - некоторая поправочная матрица. Во
всех правилах пересчета неизменным является выполнение квазинью­
тоновского условия
в<п + l)(х<п + 1) -x<n>) = g<n + 1) - g<п).
Известно, что при определенных условиях квазиньютоновские
методы сходятся сверхлинейно. Для квадратичных же функций они
дают точное значение точки минимума после конечного числа ите­
раций, которое не превышает 1 т.
Первый из квазиньютоновских методов был предложен в 1959 г.
Дэвидоном. С тех пор эти методы непрерывно совершенствовались и
к настоящему времени стали одними из наиболее популярных и широко
применяемых на практике. Весьма интересное и содержательное обсуж­
дение квазиньютоновских методов содержится в книгах [28, 40, 112].
Замечание. В некоторых вариантах квазиньютоновских мето­
дов направление спуска вычисляется по формуле р<п> = -н<п>g<11>,
где Н(n) - матрица, аппроксимирующая матрицу, обратную мат­
рице Гессе.
3. Метод Ньютона и квазиньютоновские методы при наличии
помех. Вычислительные ошибки (помехи) оказывают существенное
влияние на поведение метода Ньютона. Природа этих ошибок может
быть различной (вычисление g<11>, решение системы уравнений
G<11>p<11>= -g<п> и др.). В результате вместо ньютоновского направления
р<п> получается направление р~п), вычисленное с погрешностью Е =
= IP(n) - р~п) 1 . Как известно, метод Ньютона сходится, вообще говоря,
лишь в малой окрестности И точки минимума. В случае, когда радиус
этой окрестности меньше Е, очередное приближение х<п + I) =
1 Естественно, что это верно только при отсутствии вычислительной погрешности.
334

336. § 10.5. Метод сопряженных градиентов
= х<п> + а.пр~п) скорее всего окажется вне окрестности И и метод не
будет сходиться. Таким образом, метод Ньютона сохраняет свои пре­
имущества лишь при высокой точности вычислений.
Квазиньютоновские методы оказываются весьма чувствительны
к ошибкам в вычислении градиента. Причина здесь состоит в том, что
в основе этих методов лежит идея восстановления матрицы Гессе по
результатам вычисления градиента f'(x) в точках х<п>. Как и в методе
Ньютона, здесь необходимо очень аккуратное вычисление градиента.
§ 10.5. Метод сопр1женных градиентов
Метод Ньютона и квазиньютоновские методы, обсуждавшиеся
в§ I0.4, весьма эффективны как средство решения задач безусловной
минимизации. Однако они предъявляют довольно высокие требования к
объему используемой памяти компьютера. Это связано с тем, что выбор
направления поиска р<п> требует решения систем линейных алгебраи­
ческих уравнений, а также с возникающей необходимостью хранения
матриц типа в<п>, н<п>. Поэтому при больших т использование этих
методов может оказаться невозможным. В существенной степени от
этого недостатка избавлены методы сопряженных направлений.
1. Понятие о методах сопряженных направлений. Рассмотрим
задачу минимизации квадратичной функции
1
F(x) = Z (Ах, х) - (Ь, х) (10.33)
с симметричной положительно определенной матрицей А. Напомним,
что для ее решения требуется один шаг метода Ньютона и не более чем
т шагов квазиньютоновского метода. Методы сопряженных направ­
лений также позволяют найти точку минимума функции (10.33) не
более чем за т шагов. Добиться этого удается благодаря специальному
выбору направлений поиска.
Будем говорить, что ненулевые векторыр<О>,р< 1 >, .",р<т - I) являются
взаимно сопряженными (относительно матрицы А), если (Ар<п>, p<n) = О
для всех п '* /.
Под методом сопряженных направлений для минимизации квадра­
тичной функции (10.33) будем понимать метод
х<п+ 1) =х<п) + а.пр(п) (п =О, 1, 2, "., т - 1), (10.34)
335

337. Глава 10. Методы многомерной минимизации
в котором направленияр<0J,рОJ, .. .,р<т - I) взаимно сопряжены, а шаги
а = - (g<пJ, р<пJ) g<пJ = F'(х<п1) = Ах<п) - Ь
п (Ар<п>, р(п)) •
получаются как решение задач одномерной минимизации
<рп(ап)=miп <р"(а), <рп(а) =F(х<п)+ а.р<п>).
а~О
(10.35)
Теорема 10.4. Метод сопряженных направлений позволяет найти
точку минимума квадратичной функции (10.33) не более чем за т шагов. •
Методы сопряженных направлений отличаются один от другого
способом построения сопряженных направлений. Наиболее известным
среди них является метод сопряженных градиентов.
2. Метод сопряженных градиентов. В этом методе последователь­
ность приближений вычисляют по формулам (10.34), (10.35), а направ­
ления р<п) строят по правилу
где
р(О) = -g(O); р<п + 1) = -g<п т 1) + /3"р<п), п ~ О,
(Ap(n),g(n+ 1))
13п = (Ар(п), р(п)) .
Так как p<0J = -g (О), то первый шаг этого метода совпадает с шагом
метода наискорейшего спуска. Можно показать (мы этого делать не
будем), что направления (10.36) действительно являются сопряженными
относительно матрицы А. Более того, градиенты g<п) и g<k) оказываются
ортогональными при п * k и взаимно сопряженными при lп - kl > 1.
Последнему обстоятельству метод и обязан своим названием.
Пример 10.5. Применим метод сопряженных градиентов для
минимизации квадратичной функции f(x1, х2) = х~ + 2х; - 4х1 - 4х2 из
примера 10.1.
1
Запишем/в виде 2 (Ах, х) - (Ь, х), где
А=[~ ~, Ь=[~.
Возьмем начальное приближение x<0J = (О, 0)7:
336

338. § 10.5. Метод сопряженных градиентов
1- й шаг метода совпадает с первым шагом метода наискорейшего
спуска. Поэтому (см. пример 10.l)g<0J = (-4, -4)Т,р<О> = -g<O>,x<1>=
= (4/3, 4/3)r.
2-й шаг. Вычислимg< 1 J =Ax(l) _ Ь = (-4/3, 4/3)r,
(Ap(O),g(O)) 8 '(-4/3) + 16 · (4/3) _ 1.
Ро=(Ар<О>,р<О>)= 8·4+16·4 -9,
p<1J = -g(I> + р0р<0> = (4/3, -4/3)r + (1/9)(4, 4)т = (16/9, -8/9)т;
(g(I >, p(I >) (-4/3). ( 16/9) + (4/3). (-8/9) 3
а=- =- =-·
1 (Ap(IJ,p(I}) (32/9)·(16/9)+(-32/9)·(-8/9) 8'
х<2> =x<I) + а 1 р0) = (413, 4/3)т + (3/8)(16/9, -8/9)r = (2, 1)7:
Так как g(2) =Ах(2) - Ь = О, то х =х<2) = (2, 1)r и решение оказалось
найденным за два шага. .А.
Для более рациональной организации вычислений расчетные
формулы метода сопряженных градиентов часто переписывают в экви­
валентном виде
g(O) =Ах(О) - Ь, р(О) = -g<O>,
(g(n) g<n>)
а= ,
п (Ар<п>,р<п>)'
х<п + 1) =х<п) + апр(п),
g<п + 1) =g<п> + апАр<пJ,
(g(n+ l),g(n+ 1))
Рп = (g<nJ, g<n>) '
p(n + 1) = -g<n + 1) + РпР(п).
(10.36)
(10.37)
(10.38)
(10.39)
(10.40)
(10.41)
3. Метод сопряженных градиентов для минимизации иеквадра­
тичных функций. Для минимизации произвольной гладкой функции f
расчетные формулы метода сопряженных градиентов модифицируют.
Сначала полагают
g(O) = j'(x<D)), р(О) = -g<O>,
а затем при п ~ О вычисления производят по формулам
q>n(an) = min q>n(а), где q>n(a) = f(x(n) + ap<n)).
(l ~о
х(п+ 1) =х(п) + апр(п),
(10.42)
337

339. Глава 10. Методы многомерной минимизации
g(n + 1) = f'(х<п + 1)),
_ (g(n+ l),g(n+ 1))
~п - ( (п) (n)) 'g ,g
p<n + 1) = -g<n + 1) + ~пР(п).
Итерационный процесс здесь уже не оканчивается после конечного
числа шагов, а направления р<п> не являются, вообще говоря, сопря­
женными относительно некоторой матрицы.
Решение задач одномерной минимизации (10.42) приходится осуще­
ствлять численно Отметим также то, что часто в методе сопряженных
градиентов при п = т, 2т, 3т, ... коэффициент ~п _ 1 не вычисляют,
а полагают равным нулю. При этом очередной шаг производят факти­
чески методом наискорейшего спуска. Такое «обновление» метода
позволяет уменьшить влияние вычислительной погрешности.
Замечание. Иногда используется вариант метода, в котором
коэффициент ~п вычисляют по формуле
(g<п + 1>, g< п + 1) - g(п >)
~п = (g<n>, g(n>) '
Для сильно выпуклой гладкой функции f при некоторых дополни­
тельных условиях метод сопряженных градиентов обладает высокой
сверхлинейной скоростью сходимости. В то же время его трудоемкость
невысока и сравнима с трудоемкостью метода наискорейшего спуска.
Как показывает вычислительная практика, он незначительно уступает по
эффективности квазиньютоновским методам, но предъявляет значи­
тельно меньшие требования к используемой памяти компьютера.
В случае, когда решается задача минимизации функции с очень большим
числом переменных, метод сопряженных градиентов, по-видимому,
является единственным подходящим универсальным методом .
§ 10.6. Методы минимизации
без вычисления производных
1. Методы прямого поиска. Метод деформируемого много­
гранника. Существует большой класс методов минимизации, каждый из
которых основан на сравнении значений целевой функции в последова­
тельно вычисляемых пробных точках. Это так называемые методы
прямого поиска. Обычно они применяются тогда, когда в любой окрест­
ности точки локального минимума целевая функция не является гладкой,
338

340. § 10.6. Методы минимизации без вычисления производных
а множество точек, в которых она недифференцируема, имеет слишком
сложную структуру. К сожалению, методы прямого поиска в боль­
шинстве случаев очень неэффективны. Обращаться к ним, по-видимому,
имеет смысл только тогда, когда есть уверенность, что никакие другие
подходы к решению задачи минимизации невозможны.
Рассмотрим кратко один из наиболее известных методов прямого
поиска - метод деформируемого многогранника. Сначала необходимо
(0) (О) (О) (0) (0)
задать т + 1 точку х 1 ,х2 , ... ,Хт+ 1 так, чтобы векторы х2 -х 1 ,
(0) (О) (О) (О) w
х3 -х1 , •••, хт+ 1 -х 1 были линеино независимы. Тогда эти точки
можно интерпретировать как вершины т-мерного многогранника.
Обычно начальный многогранник выбирают правильным.
Опишем очередную (п + 1)-ю итерацию простейшего варианта
(п) (п) (п)
метода. Будем предполагать, что точки х 1 , х2 , .•. , хт + 1 являются вер-
шинами многогранника, полученного на предыдущей итерации, и зану-
мерованы так, что f (х~п» = i:nш f (х~п>), f (х~~ 1) = ry-iax f (х~п)) .
1S1Sm+1 1S1Sm+1
Точку х~~ 1 отбрасывают как самую неудачную. Затем вычисляют
1 т ()
«центр тяжести» оставшихся точек по формуле и<п> =;;; Lx;n и строят
i=l
пробную точку х~;> = u<п> + (u<nJ _x~~ 1), отразив симметрично вершину
х~~ 1 относительно точки u<п>. Геометрическая иллюстрация этой опе­
рации длят= 2 приведена на рис.10.9, а. Заметим, что в плоском случае
роль многогранника играет треугольник.
Далее возможны три случая.
а)
х<п>
1
х (n)
пр
х (n)
2
х<п>
1
б)
Рис. 10.9
~(n)
х<п>
1
11)
339

341. Глава 10. Методы многомерной минимизации
Случай : f(xn» <.5,./(х~;)) <.5,./(х~». т.е. пробная точка не привела
к уменьшению значения целевой функции, но и не стала «худшей»
б (п) (п) (п) (п)
в на оре х1 , х2 , •.. , хт , xnp . В этом случае точку признают удовле-
- (п) (п)
творительнои и хт + 1 заменяют на xnp .
- (п) / (п)
Случаи 2: f(x"P) < (х 1 ) , т.е. выбор пробной точки привел
к уменьшению значения целевой функции. Тогда направление отра­
жения считают удачным и делают попытку «растянуты> многогранник в
этом направлении с коэффициентом растяжения р > l (обычно 2 <.5,. р <.5,. 3).
Находят точку х~п) = и(п) + Р(и(п) -х~~ 1). Если f (x~n)) </(х~;)), то рас-
тяжение прошло удачно и точку х~~ 1 , заменяют на х~п). В противном
случае растяжение было неудачным и производят замену х~~ 1 на х~;).
На рис. 10.9, б показано «растяжение» с коэффициентом р = 2.
Случай 3: f(x~;»>f(x~». В этом случае считают, что много­
гранник следует сжать. Если f (x~;)) >/ (х~~ 1), то вершину х~~ 1
заменяют точкой х(п) = и(п) -у(и(п) -х(п) ) Если же f(x(n)) </(х(п) )с 1 т + 1 • пр - т + 1 •
то х~~ 1 заменяют на х~:) = и(п) +у(и(п) - х~~ 1) . Здесь О < у < l, у -
коэффициент сжатия (обычно у = l/2). На рис. 10.9, в показано
«сжатие» с коэффициентом у = l/2.
Помимо операций отражения, сжатия и растяжения периодически
(после выполнения определенного числа итераций) производят опе­
рацию замены текущего многогранника правильным многогранником -
так называемое восстановление. При восстановлении сохраняются
лишь две лучшие точки последнего многогранника. Расстояние между
этими точками принимают за длину ребра вновь генерируемого пра­
вильного многогранника. Эта операция позволяет ликвидировать
излишние деформации, возникаюшие в ходе итераций.
Известно большое число различных модификаций этого метода.
Подробно они описаны в книгах [28, 112]. Там же указаны различные
критерии окончания.
2. Методы минимизации гладких функций, использующие
конечно-разностные аппроксимации производных. Довольно часто
в приложениях возникает необходимость в минимизации функций,
обладающих достаточным числом производных, которые тем не менее
340

342. § 10.7. Нелинейная задача метода наименьших квадратов
недоступны для прямого вычисления. Например. такая ситуация имеет
место тогда, когда значение функции является результатом решения
сложной математической задачи. В этом случае приходится применять
алгоритмы, использующие лишь вычисляемые в различных точках зна­
чения функции f Здесь обращение к методам прямого поиска (типа
метода деформируемого многогранника), специально разработанным
для минимизации негладких функций, вряд ли целесообразно, так как
эти методы не позволяют извлекать никакой выгоды из возможной
гладкости функции. Часто существенно лучший результат можно
получить, заменив в одном из алгоритмов спуска используемые в нем
производные их аппроксимациями в соответствии с формулами чис­
ленного дифференцирования (см. гл. 12). Например, для производной
r;. простейшая аппроксимация такова:
]
f;}x 1,x2, ...,xm)~k(f(x1, .•• ,Xj-l•xj+hj,Xj+I• ...,хт)-/(х1,х2, ...,хт)).
)
Подобная модификация алгоритмов не является тривиальной и
требует достаточной осторожности в реализации. Это связано с
высокой чувствительностью формул численного дифференцирования к
ошибкам в вычислении функции (см. § 12.3). Более подробное обсуж­
дение методов минимизации, использующих конечно-разностное
аппроксимации производных, можно найти в [28] и [40]. В заключение
все же отметим, что конечно-разностные аппроксимации производных
используются в алгоритмах минимизации тогда, когда аналитическое
вычисление производных невозможно. Если же производные можно
вычислить аналитически, то усилия, потраченные на такое вычисление,
как правило, окупаются.
§ 1О.7. Неnинейна1 задача
метода наименьших квадратов
1. Нелинейная задача метода наименьших квадратов. Среди
задач безусловной минимизации особое место занимает задача миними­
зации функций вида
(10.43)
гдеj(х) = (/i(x),h.(x), ...,fzv(x))Т, f;(x) (:;;; i:;;; N) - некоторые функции т
переменных х =(х1 , х2, .•., хт)Т. Как правило, N ~ т; часто N » т.
341

343. Глава 10. Методы многомерной минимизации
Необходимость в минимизации таких функций возникает, например,
при использовании метода наименьших квадратов для решении задачи
аппроксимации функции (см. гл. 11) либо для решения проблемы иден­
тификации математической модели по данным эксперимента.
К поиску точки минимума функции вида (10.43) может быть сведена
и задача решения системы нелинейных уравнений
/;(х) = О, 1::; i::; N,
то есть системы
/(х)=О. (10.44)
Действительно, если решение х системы (10.44) существует, то оно
совпадает с точкой глобального минимума функции (10.43), причем
F( х )= О. В случае, когда число уравнений в системе превышает число
неизвестных, мы имеем дело с переопределенной системой, которая,
скорее всего не имеет решений. В этом случае минимизация функции F
позволяет найти вектор х , для которого
/(х)::::О
с минимальной нормой невязки/( х ).
Для минимизации функции (10.43), в принципе, можно применить
любой из универсальных методов минимизации. Однако, как правило,
этого не делают, а используют алгоритмы, разработанные специально
для решения нелинейной задачи метода наименьших квадратов. В част­
ности, это связано с тем, что градиент g(x) = F'(x) и матрица Гессе
G(x) = F"(x) для функции (10.43) имеют специальный вид:
g(x) = J (х)т/(х); (10.45)
N
G(x) =J(x)TJ(x) + Q(x), где Q(x) = L f;(x)G;(x).
i=I
(10.46)
Здесь J(x) = f'(x) - это матрица Якоби для вектор-функции / с
дf;
элементами Jij = дх'· (х), 1$ i $ N, 1$) $ т. 1 Матрицы G;(x) ( 1$ i $ N) -
1
д2J:·
это матрицы Гессе для функций/; с элементами (G,)k1·= д-д' (х), 1$ k $ т,
xk xj
1$) $ т.
2. Метод Гаусса-Ньютона. Будем рассматриать задачу минимиза­
ции функции (10.43) как задачу решения переопределенной системы
1 Обратим внимание на то, что в отличие от матрицы Гессе (7.3) матрица J(x) уже не
квадратная, а прямоугольная .
342

344. § 10.7. Нелинейная задача метода наименьших квадратов
(10.44). Пусть некоторое приближение x(k> к точке минимума найдено.
Аналогично тому, как мы поступали в § 7.3, произведем линеаризацию
вектор-функции / в этой точке, заменив ее главной линейной частью
разложения по формуле Тейлора в точке x(kJ:
f(x) ""f(x(k)) +J<k>(x -x<k>);
здесь и всюду в этом параграфе J(k) = J (x<k>) =f'(JIЛ). За следующее
приближение x(k + I) к решению примем точку минимума функции
Fk(x) = ~ llflx(k)) +J<k>(x-x(k))ll;.
Для этого положим р = х - x(k> и найдем вектор p<k + 1>такой, что
llflx<k)) + J(k)p(k+ '>11; = min llflx(k)) + J(k)Pll;. (10.47)
ре Rm
Если решение этой задачи не является единственным, то за p<k + 1)
принимается решение с минимальной нормой.
После того, как p<k + t) найдено, приближение x(k + 1> вычисляется по
формуле
x(k + ) =x(k) +p<k + 1),
Заметим, что задача (10.47)- это линейная задача метода наименьших
квадратов, предназначенная для решения переопределенной системы
J(x(k>)p = -f(x<n>).
Ее решение p<k + 1> может быть найдено одним из рассмотренных в
§ 5.12 методов.
З а м е ч а н и е 1. Можно показать, что в случае, когда решение p<k+ t)
задачи (10.47) ненулевое, оно является направлением спуска для
функции F.
Замечание 2. В случае, когда т = N, а матрица Якоби J(x)
невырождена, метод Гаусса-Ньютона превращается в метод Нью­
тона, рассмотренный в § 7.3.
3. Модифицированный метод Гаусса-Ньютона. Как и метод Нью­
тона, метод Гаусса-Ньютона обладает лишь локальной сходимостью. Для
того, чтобы расширить область сходимости метода ero модифицируют.
После того, как решение линейной задачи метода наименьших квад­
ратов (10.47) найдено, полагают
x<k + t) = x<k> + akp(k + '>,
343

345. Глава 10. Методы многомерной минимизации
где ak > О вычисляется как решение задачи одномерной минимизации
<pk(ak) = min <i>k (а), где <pk(a) =llлx<k» + ap(k+ 1>11;.
а~О
4. Другие методы. Коротко обсудим другие подходы к решению
нелинейной задачи метода наименьших квадратов.
Заметим, что искомое решение должно удовлетворять необходимому
условию экстремума F'(x) =О. В силу формулы (10.45) это условие при-
нимает вид
(10.47)
Применяя для решения этой системы нелинейных уравнений класси­
ческий метод Ньютона, мы приходим к следующему итерационному
методу
dkJp<k + 1) =_[J<k>] r/(x(k)),
(k + 1) (k) + (k + 1)
х =х р .
(10.48)
(10.49)
Матрица G(k) = G(x<k>), которую следовало бы использовать в этом
методе, весьма громоздка и неудобна для вычислений. Согласно фор­
муле (10.46) она имеет вид
N
G(k) = [J<kyJ(k) + Q(k)' где Q(k) = L f;(x(k1>G;(x(k)).
i=I
Дrlя вычисления слагаемоm (lk) на каждой итерации требуется
вычисление всех вторых частных производных всех функций f;, 1~ i ~ N.
Этого всячески стараются избегать.
Обратим внимание на то, что если получено достаточно хорошее
приближение x<k) такое, что llлx<k»ll2 "'О, тоf;(x<k))"' О для всех i = 1,
2, ..., N. В этом случае Q(k) "'О и dk)"' [J(k)]TJ(k).
Замена в итерационном методе (10.48), (10.49) матрицы G(k) на мат­
рицу [J(k)]TJ(k) приводит к итерационному методу
[J(k)] тJ(k)p(k + 1) = _J (x<k>{лx<k>);
x<k + 1) = x<k> + p<k + IJ,
(10.50)
(10.51)
который эквивалентен методу
системы (10.50) совпадают
llлx<k>) + J(x<k>)Pll;.
Гаусса-Ньютона, так как решения
с точками минимума функции
Распространенной альтернативой методу Гаусса-Зейделя является
метод Левенберга-Маркардта. В этом методе матрица G(k) заменяется
344

346. § 10.8. Дополнительные замечания
матрицей [J(k>yjk> +а~, где О~ ak - параметр, и метод принимает
Вид
([J(k>]Tjk + a~)/k+ 1) = -[JЩ]Tf(x(k»,
х<* + t) = x<AJ + р<* + 1).
Методы Гаусса-Ньютона и Левенберга-Маркардта исходят из
того, что вблизи от решения невязка/(х<*>) мала и поэтому слагаемым
(i*> в формуле для вычисления G(k) можно пренебречь. Такие задачи
обычно называют задачами с малыми невязками.
Однако на практике часто встречаются задачи с большими невяз­
ками, в которых это слагаемое существенно. В этом случае строят спе­
циальные квазиньютоновские приближения м<*J к матрице (i*> и итера­
ции проводят по формулам
([J(k))Тj*> + м<*>)р(k + 1) = - J(x(k>{f(x(k))'
х<* + 1) = х<*> + p<k + 1).
Достаточно подробное обсуждение квазиньютоновских методов и
других методов решения нелинейной задачи метода наименьших квад­
ратов можно найти в книгах [28, 40].
§ 10.8. Дополнительные замечани1
1. Естественно, что в данной книге содержится лишь краткое введение
в методы решения задач безусловной минимизации. Более подробное изло­
жение можно найти, например в [6, 20, 28, 40, 78, 80, 94, 112 и др.].
2. Задачи условной минимизации. Множество Х, на котором
минимизируется функция f, часто задается с помощью системы нера­
венств вида
g;(x1, х2, "., хт) 2 О, i = 1, 2, "., k.
Если целевая функция f и задающие множество Х функции g,
линейны, то задачу минимизации называют задачей линейного про­
граммирования. Если же хотя бы одна из этих функций нелинейна, то
говорят о задаче нелинейного программирования.
Обсуждение методов решения задач условной минимизации при
всей их важности выходит за рамки данной книги. Укажем, например
на книги [20, 28, 94, 112), содержащие достаточно подробное и доступное
введение в соответствующие методы.
3. Особый класс задач составляют так называемые задачи дис­
кретной минимизации. В этих задачах множество Х, на котором миними-
345

347. Глава 10. Методы многомерной минимизации
зируется функция/, является конечным или счетным. Часто Х - мно­
жество точек с целочисленными координатами, удовлетворяющими
некоторым ограничениям. Методы решения таких задач описаны,
например в [94).
4. Авторы рекомендуют обратить внимание на книгу [28), в особен­
ности на ее последние главы («Моделирование», «Практические
вопросы» и «Вопросы и ответы»). В них содержится большое число
весьма интересных замечаний, полезных рекомендаций и советов для
широкого круга специалистов, заинтересованных в решении практи­
ческих задач минимизации.
346

348. Глава 11
ПРИБЛИЖЕНИЕ ФУНКЦИЙ
И СМЕЖНЫЕ ВОПРОСЫ
В этой главе рассматриваются наиболее важные и часто встречающиеся
в приложениях методы приближения функций одной переменной. Зна­
чительное внимание уделено интерполяции, причем рассматривается
интерполяция не только алгебраическими многочленами, но и триго­
нометрическими многочленами, а также интерполяция сплайнами.
Довольно подробно обсуждается метод наименьших квадратов, широко
используемый в практике инженерных расчетов. Дается понятие о
наилучшем равномерном приближении и дробно-рациональных аппрок­
симациях.
В главу включены также некоторые вопросы вычислительной мате­
матики, имеющие непосредственное отношение к методам аппрокси­
мации (приближения) функций. Эт