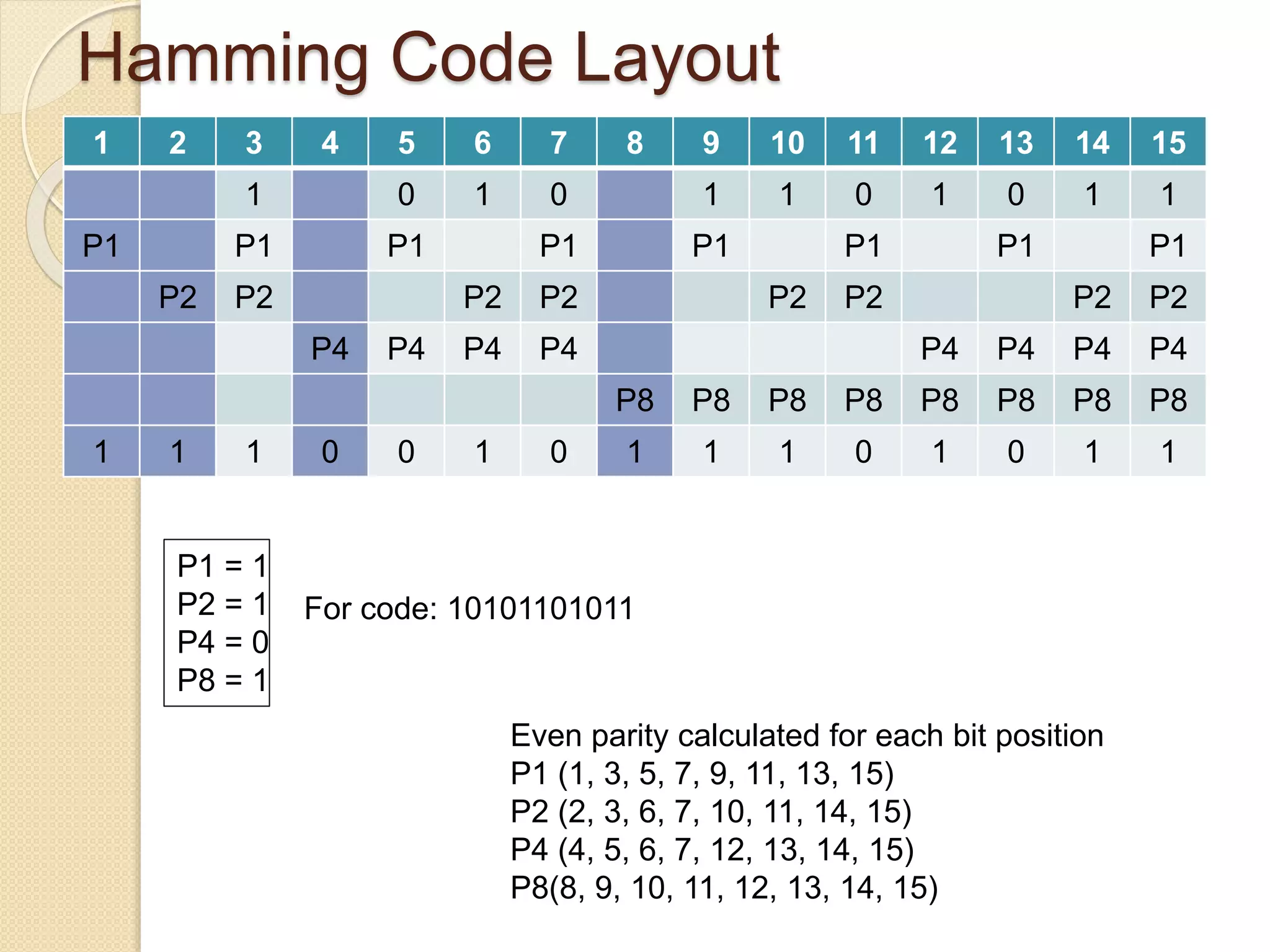
Hamming codes can detect up to two simultaneous bit errors and correct single-bit errors. They work by adding parity bits calculated for groups of bits in positions that are powers of 2. To encode data, parity bits are set to 1 or 0 based on whether the total number of 1s in the corresponding bit positions is odd or even. To decode, the received bits are used to recalculate the parity bits and identify any discrepancies, allowing the location and correction of errors.

1. Hamming Code

2. Error Detecting and Correcting
Code
 Parity code
◦ Detect odd number of errors
◦ Cannot correct any errors
 Hamming Code
◦ Detect up to two simultaneous bit errors
◦ Correct single-bit errors

3. Hamming Code
 For each integer m > 2
◦ Code exists with m parity bits and 2m – m – 1
 Basically
◦ Parity bit for odd bits
◦ Parity bit for each two bits
◦ Parity bit for each four bits
◦ Parity bit for each eight bits
◦ Parity bit for each group of bits that are power of
2
 1, 2, 4, 8, 16, 32, …

4. Calculating Hamming Code
1. Mark all bit positions that are powers of two parity bit
1, 2, 4, 8, 16, 32, 64, etc
2. All other bit positions are for the data to be encoded
3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, etc.
3. Each parity bit calculates the parity for some of the bits in
the code word
The position of the parity bit determines the sequence of bits that it
alternately checks and skips
Position 1: check 1 bit, skip 1 bit, check 1 bit, skip 1 bit, etc.
(1,3,5,7,9,11,13,15,...)
Position 2: check 2 bits, skip 2 bits, check 2 bits, skip 2 bits, etc.
(2,3,6,7,10,11,14,15,...)
Position 4: check 4 bits, skip 4 bits, check 4 bits, skip 4 bits, etc.
(4,5,6,7,12,13,14,15,20,21,22,23,...)
Position 8: check 8 bits, skip 8 bits, check 8 bits, skip 8 bits, etc.
(8-15,24-31,40-47,...)
4. Set a parity bit to 1 if the total number of ones in the
positions it checks is odd. Set a parity bit to 0 if the total
number of ones in the positions it checks is even

5. Hamming Code Layout
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 2 3 4 5 6 7 8 9 10 11
Pos 20=1 21=2 22=4 23=8
1 1 0 0 0
2 0 1 0 0
3 1 1 0 0
4 0 0 1 0
5 1 0 1 0
6 0 1 1 0
7 1 1 1 0
8 0 0 0 1
9 1 0 0 1
10 0 1 0 1
11 1 1 0 1
12 0 0 1 1
13 1 0 1 1
14 0 1 1 1
15 1 1 1 1
Even parity calculated for each bit position
P1 (1, 3, 5, 7, 9, 11, 13, 15)
P2 (2, 3, 6, 7, 10, 11, 14, 15)
P4 (4, 5, 6, 7, 12, 13, 14, 15)
P8(8, 9, 10, 11, 12, 13, 14, 15)

6. Hamming Code Layout
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0 1 0 1 1 0 1 0 1 1
P1 P1 P1 P1 P1 P1 P1 P1
P2 P2 P2 P2 P2 P2 P2 P2
P4 P4 P4 P4 P4 P4 P4 P4
P8 P8 P8 P8 P8 P8 P8 P8
1 1 1 0 0 1 0 1 1 1 0 1 0 1 1
Even parity calculated for each bit position
P1 (1, 3, 5, 7, 9, 11, 13, 15)
P2 (2, 3, 6, 7, 10, 11, 14, 15)
P4 (4, 5, 6, 7, 12, 13, 14, 15)
P8(8, 9, 10, 11, 12, 13, 14, 15)
For code: 10101101011
P1 = 1
P2 = 1
P4 = 0
P8 = 1

7. Hamming Code (1 error)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0 1 0 1 1 0 1 0 1 1
P1 P1 P1 P1 P1 P1 P1 P1
P2 P2 P2 P2 P2 P2 P2 P2
P4 P4 P4 P4 P4 P4 P4 P4
P8 P8 P8 P8 P8 P8 P8 P8
1 1 1 0 0 1 0 1 1 1 0 1 0 1 1
1 1 1 0 0 1 0 1 1 1 0 1 0 0 1
Even parity calculated for each bit position
P1 (1, 3, 5, 7, 9, 11, 13, 15)
P2 (2, 3, 6, 7, 10, 11, 14, 15)
P4 (4, 5, 6, 7, 12, 13, 14, 15)
P8(8, 9, 10, 11, 12, 13, 14, 15)
A S
P1 = 1 1
P2 = 1 0
P4 = 0 1
P8 = 1 0
Xmit
Rec
2, 4, and 8 incorrect
2 + 4 + 8 = 14
A = Actual Parity
S = Should be
Parity

8. Hamming Code (2 errors)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0 1 0 1 1 0 1 0 1 1
P1 P1 P1 P1 P1 P1 P1 P1
P2 P2 P2 P2 P2 P2 P2 P2
P4 P4 P4 P4 P4 P4 P4 P4
P8 P8 P8 P8 P8 P8 P8 P8
1 1 1 0 0 1 0 1 1 1 0 1 0 1 1
1 1 1 0 0 1 0 1 0 1 0 1 0 0 1
Even parity calculated for each bit position
P1 (1, 3, 5, 7, 9, 11, 13, 15)
P2 (2, 3, 6, 7, 10, 11, 14, 15)
P4 (4, 5, 6, 7, 12, 13, 14, 15)
P8(8, 9, 10, 11, 12, 13, 14, 15)
A S
P1 = 1 0
P2 = 1 0
P4 = 0 1
P8 = 1 1
Xmit
Rec
1,2, and 4 incorrect
1 + 2 + 4 = 7
Fix 7, will still have parity problem
A = Actual Parity
S = Should be
Parity

9. Example
 A byte of data: 10011010
 Create the data word, leaving spaces for the parity bits:
_ _ 1 _ 0 0 1 _ 1 0 1 0
 Calculate the parity for each parity bit (a ? represents the bit
position being set):
◦ Position 1 checks bits 1,3,5,7,9,11:
? _ 1 _ 0 0 1 _ 1 0 1 0. Even parity so set position 1 to a 0:
0 _ 1 _ 0 0 1 _ 1 0 1 0
◦ Position 2 checks bits 2,3,6,7,10,11:
0 ? 1 _ 0 0 1 _ 1 0 1 0. Odd parity so set position 2 to a 1:
0 1 1 _ 0 0 1 _ 1 0 1 0
◦ Position 4 checks bits 4,5,6,7,12:
0 1 1 ? 0 0 1 _ 1 0 1 0. Odd parity so set position 4 to a 1:
0 1 1 1 0 0 1 _ 1 0 1 0
◦ Position 8 checks bits 8,9,10,11,12:
0 1 1 1 0 0 1 ? 1 0 1 0. Even parity so set position 8 to a 0:
0 1 1 1 0 0 1 0 1 0 1 0
◦ Code word: 011100101010

10. Finding and Fixing a Bad Bit
123456789012
 Transmitted word: 011100101010
 Received word: 011100101110
 Calculate the parity bits from received
word
SB A
◦ P1 (1, 3, 5, 7, 9, 11) = 0 0
1
◦ P2 (2, 3, 6, 7, 10, 11) = 0 1
2
◦ P4 (4, 5, 6, 7, 12) = 1 1 4
◦ P8 (8, 9, 10, 11, 12) = 1 0
8
 2 + 8 = 10

11. Finding and Fixing a Bad Bit
123456789012
 Transmitted word:
 Received word: 010101100011
 Calculate the parity bits from received
word
SB A
◦ P1 (1, 3, 5, 7, 9, 11) = 0 0
◦ P2 (2, 3, 6, 7, 10, 11) = 0 1
◦ P4 (4, 5, 6, 7, 12) = 0 1
◦ P8 (8, 9, 10, 11, 12) = 0 0
 Bit positions 2 & 4 are incorrect
2 + 4 = 6
 Correct code is 010100100011

12. Finding and Fixing a Bad Bit
123456789012
 Transmitted word:
 Received word: 111110001100
 Calculate the parity bits from received
word
SB A
◦ P1 (1, 3, 5, 7, 9, 11) = 0 1
◦ P2 (2, 3, 6, 7, 10, 11) = 1 1
◦ P4 (4, 5, 6, 7, 12) = 0 1
◦ P8 (8, 9, 10, 11, 12) = 0 0
 Bit positions 1 & 4 are incorrect
1 + 4 = 5
 Correct code is 111100001100

13. Finding and Fixing a Bad Bit
123456789012
 Transmitted word:
 Received word: 000010001010
 Calculate the parity bits from received
word
SB A
◦ P1 (1, 3, 5, 7, 9, 11) = 1 0
◦ P2 (2, 3, 6, 7, 10, 11) = 1 0
◦ P4 (4, 5, 6, 7, 12) = 1 0
◦ P8 (8, 9, 10, 11, 12) = 0 0
 Bit positions 1, 2 & 4 are incorrect
1 + 2 + 4 = 7
 Correct code is: 000010101010