3. reliability modelling

01-02-2012

DEFINITIONS

System is a collection of components
configured to realize a given task.
Reliability Engineering Centre

This can be described through:
Reliability Modeling and • Structure Function (Mathematical)
Evaluation
E l ti • L i Di
Logic Diagram (Vi(Visual)
l)

1 2
Indian Institute of Technology, Kharagpur Indian Institute of Technology, Kharagpur

TYPE OF SYSTEMS SYSTEM RELIABILITY MODELLING
Systems are of two types: • In case of non-maintained systems, system
reliability or Mean Time To Failure ( MTTF) is
• Non-maintained (Reliability and associated generally the main criteria of system
performance.


metrics)
• On the other hand, in case of maintained
• Maintained (Availability and associated systems, maintainability design (MD) goes
metrics) hand-in-hand
hand in hand with its design for reliability
• Appropriate stochastic models are very (DFR) and the system needs to be designed for
both reliability and maintainability, or for
much different for these two types of MTTF and MTTR, and
systems! • Many a times, system availability is often
optimized within the resources available for
system design.
3 4

1

01-02-2012

SYSTEM HIERARCHY SYSTEM MODELLING

• All systems have a built-in hierarchy • One can model system in any of the following
ways using failure/success criterion:
Black Box Approach

In this approach, the state of system is described either in
terms of the two states (working/ failed) or more than two
states without linking them to the components of the
system.
White Box Approach
In this approach, one models the state of the system
specifically in terms of the states of various components of
the system.

5 6

SYSTEM MODELLING SYSTEM MODELLING
White Box Modeling: Linking the system performance to the
 The first one is called Forward (or Bottom up) approach. The other
is called Backward (top-down) approach. failures/success at item level can be done
qualitatively or quantitatively.


1. In the forward approach, one starts with events
(success or failure) at item level and then In the qualitative analysis, the focus is on causal
proceeds forward to system level to evaluate the
consequences of such events on system relationships that link the item level events to
performance. system events or vice-versa.
In quantitative analysis, one obtains various
2. In the Backward approach, one starts at system
level and proceeds downward to the item level measures of system performance (e.g., system
to link system performance to success/failures at reliability) in terms of items performance. (e.g.,
item level. item reliabilities)
7 8

2

01-02-2012

BLOCK DIAGRAM OF A SYSTEM
GRAPHICAL REPRESENTATION
• Since the system modeling is done on the basis of
• There are two ways of graphically representing the functional interrelationship of the constituent items
functional relationship in a Qualitative analysis of a in relation to the overall functioning of the system,

system. The first one is Block diagram or Reliability one has to keep the hierarchy of the system in view.
Logic Diagram (RLD) approach. An RLD indicates • Therefore, we must consider the success of the
which components of the system must operate for
system vis-à-vis the success of the constituent
vis à vis
successful operation of the system. The other approach
involves indication of which components must fail subsystems and then success of each subsystem is
before the system fails. This graphical representation considered vis-a-vis the success of the constituting
is done through Fault Tree Logic Diagram. Block components. This exercise will eventually result in
Diagram approach is optimistic approach of a Block Diagram of the system.
modelling whereas the FTA is pessimistic approach
of Modelling.


RELIABILITY LOGIC/BLOCK/NETWORK DIAGRAM BLOCK DIAGRAM OF A JET ENGINE
• A diagram which shows the logical relationships of system • Jet Engine
success (or failure) with success (or failure) of its
– Fuel Supply System
constituent parts is termed as RLD/RBD/NRLD.
• Fuel Pump


• Fuel Filter
• RLD indicates that which component(s) in a system must – Carburetor
operate without any failure for successful operation of the • Jet
system.
system • Other Components
– Ignition System (2)
• To develop RLD and reliability analysis thereof require • LV
understanding and depiction of operational relationships or • HV
logical interrelationships amongst its constituent items
(subsystems, units or elements or parts.)

11

3

01-02-2012

ASSUMPTION IN MODELING INDEPENDENT FAILURES
• All elements and systems can be either in operating • Failure times of components are influenced by
or failed state, i.e., two state modeling. environmental conditions. As the environment
• All elements are in operating state initially except gets harsher, the time to failure of component

possibly in the case of redundancy. decreases.
• States of all elements are statistically independent. • If the components of a system share the same
(Failure of one element does not affect the probability environment, failure times of components
of failure of other elements). become statistically dependent.
• The reliabilities of all constituent components are • However, if the dependence is weak, or the
known through some “reliability analysis”. components are located far apart, one can
ignore dependence and treat the failure times as
being statistically independent.

13

INDEPENDENT FAILURES

• The advantage of this assumption is that
the failure times of a component can be


modelled separately using Univariate
failure distribution functions. Reliability Models
• If the dependence is significantsignificant,
multivariate failure distributions must be
used and the analysis becomes much more
complicated.

16

4

01-02-2012

VARIOUS SYSTEM MODELS Series & Parallel Systems
Now we will consider various system Series System Parallel System
models that can be built for a given
non-redundant system fully redundant system
situation. Among these system models are

(all components must work for (all components must fail for system
series, parallel, series-parallel and system success) failure)

parallel-series, k-out-of-m:G, standby, ,
TR1, 10 kVA TR1, 20 kVA
partial standby , non-series parallel model 15 kVA 15 kVA
etc. We will consider these one by one and Load Load
derive system reliability and system MTTF TR2, 10 kVA TR2, 20 kVA
for these configurations.
1
1 2
2
18


Series System Example:
Let R = P [Success] A system consists of 10 identical components, all of
1 2 Q = P [Failure] which must work for system success. What is the
system reliability if each component has a reliability of
R+Q=1


0.95?
R s  R1  R 2
n Qs  1  R S Component reliability, R = 0.95
 Ri
i 1
 1  R1  R 2 Number of components, n = 10
components

product rule of reliability  1 - (1 - Q1 )(1  Q 2 )
Using Product Rule of Reliability,
 Q1  Q 2  Q 1  Q 2
S System Reliability, Rs = Rn
S = (0.95)10 = 0.5987
R1 R2
Q1 Q2

20
19


5

01-02-2012

Series System Series Model
If each component
has a reliability of
0.9.
1.0
0.9
0.999
• Most common and an important reliability
Number of Reliability
Components 0.8 model.

0.7
• Series system has no redundancy since a
tem Reliability

1 0.9
2 0.81 0.6
3 0.729 0.5
0.98
failure of any component causes failure of
4 0.6561
5 0.59049
0 59049
0.4
system.
the entire system
Syst

0.3
10 0.348678
20 0.121577 0.2
0.9
• The system reliability will be less than the
50 0.005154 0.1
0.0
reliability of least reliable component in the
0 10 20 30 40 50 60 70 model.
Number of Components

System Reliability decreases as the number of components increases in a
• System design would require high reliability
Series System. The number on the curve is the reliability of each and as few components.
component.
21 22

Series Model Parallel Redundant System
• Assuming Ei s refers to the events of units being functionally good. 1
R s  P(E 1  E 2  E 3 ...  E n )
Rs  P(E 1 ) . P(E 2 /E1 ) . P(E 3 /E 1  E 2 )... P(E n /E 1  E 2  E 3  ...  E n  1) Rs  1  QS


2
If the unit failures are independen t then,  1  Q1  Q 2
n
 1 - (1 - R 1 )(1  R 2 )
R s  P(E 1) P(E 2) P(E 3)... P(E n)   pi
i 1  R1  R 2  R1  R 2
• The above result can also be obtained using time to failure considerations product rule of
unreliability
Rs (t )  Pr(t1  t )  (t 2  t )...  (t n  t )
Rs (t )  Pr(t1  t ) Pr(t 2  t )... Pr(t n  t ) S S
n
Rs (t )   ri (t ) Q1 Q2 R1 R2
i 1

23 24

6

01-02-2012

Example: Parallel System
A system is to be designed with an overall reliability of 0.999 using
components having individual reliabilities of 0.7. What is the Reliability of each component is 0.7
minimum number of components that must be connected in parallel?

1.0
System Reliability, Rs = 0.999
Number of System
Component reliability, R = 0.7 Components Reliability 0.9

eliability
Number of components, n = ? 1 0.700000
2 0.910000
0 910000

System Re
0.8
3 0.973000
System Unreliability, Qs = 1 - Rs = 1 – 0.999 = 0.001 4 0.991900
0.7
5 0.997570
Component Unreliability, Q = 1 – R = 1 – 0.7 = 0.3 6 0.999271
0.6
Using Product Rule of Unreliability, Qs = Qn i.e. 0.001 = 7 0.999781
1 2 3 4 5 6 7 8
(0.3)n Number of Components

therefore, n = ln (0.001) / ln(0.3) = 5.74
since n is an integer, n=6 26
25

PARALLEL MODEL PARALLEL MODEL
• System reliability will be more than any of the System MTTF for Various Configurations
constituent component.
• Most common and cheapest method of reliability


improvement, if feasible or permitted.
• An additional unit will improve the MTTF by 1.5
times of the MTTF of a single unit.
unit
• There will not be much gain in system MTTF, if
number of units increased from 4 to 5 and so on.
(Law of diminishing return-See in Next Slide).

27

7

01-02-2012

Series/Parallel Systems Example:

Telcom. Repeater DG Rectifier Derive a general expression for the unreliability of the
Station 2 3 model shown below, and hence evaluate the unreliability of
1 the system if all components have a reliability of 0.8.

Power Supply
4 Cable
System
Battery Bank
Network Reduction p
Output
input
Technique
RX = R2.R3 X
1
QY = QX.Q4 4
RY = 1 - QX.Q4 Reliability Network Model (Reliability Block Diagram)
= 1 – (1-RX).(1-R4) of the System
Y 1
RS = RY.R1
29 30
29 30

m out of n Systems
Ri = 0.8 for i = 1 to 5 partially redundant system
TR1, 10 kVA
If components are identical then


3 3 2 2 3
15 kVA (R + Q) = R + 3R Q + 3RQ + Q
Load Rs = R 3 + 3R2Q
TR2, 10 kVA
Qs = 3RQ2 + Q3 = 1 - Rs

TR3, 10 kVA If components are non-identical then
Q 8 = Q 7 . Q5
= (1 - R7). Q5 2 out 3 system R1  R2  R3
= (1 - R1 . R2 . R6). Q5 2/3
= [1 - R1 . R2 . (1 - Q6)]. Q5 1 Rs = R1 R2 R3 +
= [1 - R1 . R2 . (1 - Q3 . Q4)]. Q5 R1 R2 Q3 + R1 Q2 R3 + Q1 R2 R3
2
Q8 = [1 – 0.8 x 0.8 (1 – 0.2 x 0.2)]x 0.2 = 0.07712
31 3 32
31 32

8

01-02-2012

Example: 2/3
4
2
Derive a general expression for the unreliability of the system 1 5

whose reliability model is shown below. Consider the case in 3 6
which all parallel branches of this system are fully redundant 7

with the exception of that consisting of components 4, 5 and 6 for
Q8 = Q2 . Q3
which any 2 of the branches are required for system success.
1 8 9 If Components 4, 5 and 6 are identical, each with
2/3 reliability R, R9 = R3 + 3R2Q
4
2 7
Otherwise
1 5 R 9 = R 4 R 5 R 6 + R 4 R 5 Q 6 + R 4 Q 5 R 6 + Q4 R 5 R 6
input 3 Output
6 10
R10 = R1 R8 R9
7
7
Qs = Q10 . Q7
= (1 – R10). Q7
Reliability Network Model (Reliability Block = (1 - R1 . R8 . R9). Q7
11 = [1 - R1 (1 – Q8).R9 ]. Q7
Diagram) of the System
33 = [1 - R1 (1 – Q2 .Q3). R4 R5 R6 + R4 R5 Q6 + R4 Q5 R6 + Q4 R5 R6 ]. Q7
34

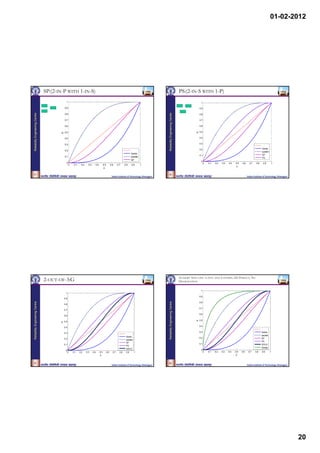
2-out-of-3:G Model RELIABILITY OF 2-OUT-OF-3:G SYSTEM
The Reliability Logic Diagram and Fault Tree diagram for Let us designate the paths in Block diagram as
2-out-of-3:G system are shown below: Obviously, T1 , T2 and T3 .


T1  E1  E 2 , T2  E1  E3 and T3  E 2  E3
where Ei is the event of unit i being good. Therefore,
system reliability is given by:
Rs  PrT1  T2  T3    PTi    PTi  T j    PTi  T j  Tk 
3

i 1 i j i j k
where,
PT1  T2   PE1  E 2   E1  E3   PE1  E 2  E3 
3
3 3
Rs   P Ti    P E1  E2  E3     PE1  E2  E3 
i 1 2 3
R s  p1 p 2  p1 p 3  p 2 p 3  2 p1 p 2 p 3

35
or R s  3 p 2  2 p 3 .

9

01-02-2012

2-out-of-3:G Model (MTTF) Exercise 3-out-of-4:G Model (MTTF)

For exponential failure distribution, we can Consider a 3 out of 4 system. The system is successful if
compute system MTTF of by: any of the path is good The success of each path
 depends on the success of two elements


2
MTTF  R s ( t ) dt 1 1
3
0 2
2 1
4
1 Out
where, 3
in 3
4

Rs  p1 p2  p1 p3  p2 p3  2 p1 p2 p3 4
2
3 4

Block Diagram Reliability logic Diagram
and for exponential failure distribution,
p i ( t )  e  t
1 1 1 2
MTTF    
1  2 1  3 2  3 1  2  3
38

Identical Units k-out of – M:G system (Using Binomial)

A system functions properly if any k out of m units function
A1  E1  E 2  E 3, A 2  E1  E 2  E 4 properly, the probability of exactly k successes out of m is
A 3  E1  E 3  E 4 A4  E 2 E3 E 4 given by,


yields, m
B(k; m, p)    p k (1  p) m  k
 
Rs  P(A1  A 2  A 3  A 4) k
 P(A1)  P(A2)  P(A3)  (PA4)  P(A Aj)  ...
( ( ( ( ( i The system remains functional as long as k, k  1, m  1, or m units
i j function . The probabilit y of system success is given by,

P(AAA )  P(A A  A 3  A 4) m
m
i j k 1 2 R s     p i (1  p) m  i
 
i j k ik  i 

Rs=P(E1E2E3)+P(E1E2E4)+P(E1E3E4)+P(E2E3E4)- 3P(E1E2E3E4) or
 
k 1 m
If the elements are identical and their failures are independent R s  1     p i (1  p) m  i
  particular ly, if the (m  k  1) is larger than k
then i0  i 
Rs=4P3-3p4
39 40

10

01-02-2012

MTTF OF K-OUT-OF-M:G SYSTEM k-out-of-m:G Model (MTTF)

1 m
1
MTTF k , m   j


j k

For identical units, for various
combinations of k and m ,(for k  m) , we
provide system MTTF for identical in the
next slide.

System MTTF for various
values of k and m

Example: System Reliability System Reliability Evaluation Using Probability Distributions

Time dependent reliability – described by probability distributions
t


 λ1 (t)dt
Reliability of Component 1 for a time period t, R1(t) = e 0


where (t) is the hazard rate of Component 1.
Block
A e  λ 1t
Rs  R A
During useful life p
g p
period of the component ()
R1(t) =

where  is constant, and is called the failure rate of Component 1.

The system reliability can be calculated as:
R s  R A  R B  R 10  R C , where R A  R 1  R 2
R B  1  1  ( R 3  R 4  R 5 )  1  ( R 6  R 7  R 8 )  ( 1  R 9 )
RC  1  C3
2 R 11 ( 1  R 11 ) 2  3 C 3 R 11 ( 1  R 11 ) 3
0


11

01-02-2012

Series Systems Parallel Systems

1
1 2 Rs = R1 . R2  product rule of reliability Qs = Q1 . Q2  product rule of unreliability
2
Considering time dependent probabilities,

t
  λ 1 (t)dt
t
  λ 2 (t)dt
Considering time dependent probabilities, t t
  λ 1 (t)dt   λ 2 (t)dt
Rs(t) = R1(t). R2(t) = e 0
e 0
Qs(t) = Q1(t). Q2(t) = [1- e 0 ].[1- e 0
]

For ‘n’ component series system with hazard rates 1(t), 2(t), …, n(t), For ‘n’ component parallel system with hazard rates 1(t), 2(t), …, n(t),
t
n t n   λ i (t)dt
also applicable if failure distributions for
Qs(t) =  [1 - e
  λ i (t)dt
Rs(t) =  e 0
different components are different
0
]
i 1 i 1

During useful life period when component failures are exponentially During useful life period when component failures are exponentially
distributed distributed
n n
cannot obtain equivalent hazard rate for
Qs(t) =  [1 - e i ]
n
λ t

n   λit where equivalent hazard rate, e =  i
Rs(t) =  e
λ it   et exponential distribution
= e i 1
= e i 1
i 1
is also constant i 1

Therefore, resulting distribution for the system is non-exponential
i.e. resulting distribution for the system is also exponential i.e. resulting hazard rate for the system is no longer constant, but a function
Indian Institute of Technology, Kharagpur
of time Indian Institute of Technology, Kharagpur

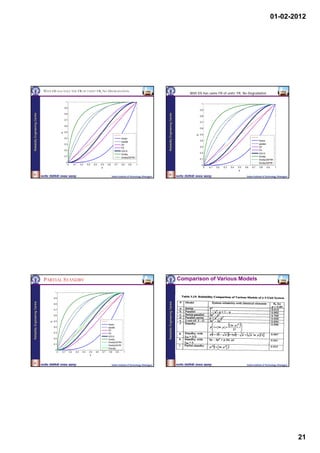
Partially Redundant (m out of n) Systems Example:

Apply Binomial Expansion A simple electronic circuit consists of 6 transistors each having a failure
rate of 10-6 f/hr, 4 diodes each having a failure rate of 0.5 x 10-6 f/hr, 3
n capacitors each having a failure rate of 0.2 x 10-6 f/hr, 10 resistors each
[R(t) + Q(t)] n =  nCr R(t) n-r Q(t) r having a failure rate of 5 x 10-6 f/hr and 2 switches each having a failure


r0
rate of 2 x 10-6 f/hr. Assuming connectors and wiring are 100% reliable,
During useful life period when component failures are evaluate the equivalent failure rate of the system and the probability of
the system surviving 1000 and 10000 hours if all components must
exponentially distributed operate for system success. n

 λt eλt Equivalent failure rate of the system, e = i1
 i
R(t) = e and Q(t) = 1 -
= 6(10-6 ) + 4(0.5 x 10-6 ) + 3(0.2 x 10-6 ) + 10(5 x 10-6 ) + 2(2 x 10-6 ) = 6.26 x 10-5
f/hr
Let see some simple examples.  t  6.26 x 10 6
x1000
Rs(1000 hr) = e e = e = 0.9393

 et  6.26 x 10 6 x10000
Rs(10,000 hr) = e = e = 0.5347


12

01-02-2012

Example:
Standby Model
Consider a system comprising of 4 identical units each having a failure
 One or more units are in standby mode waiting to take over
rate of 0.1 f/yr. Evaluate the probability of the system surviving 0.5 years
and 5 years if at least two units must operate successfully. the operation from the main operating unit as soon as the
failure of the operating unit takes place.

Using Binomial Expansion,  Decision switch senses the failure of the basic unit.
[R(t) + Q(t)] 4 = R4(t) + 4 R3(t)Q(t) + 6 R2(t)Q2(t) + 4 R(t)Q3(t) + Q4(t)  It is assumed that the operation of failure sensing and
where, R(t) = e
 λt
and Q(t) = 1 -
eλt switching on to the standby unit is instantaneous, i.e.,
operation.
uninterrupted system operation
For 2 out of 4 system,  The standby system fails only when all the system units
Rs(t) = R4(t) + 4 R3(t)Q(t) + 6 R2(t)Q2(t) including the standby units have failed.
 The reliability of such system will be higher than the
 4 λt  3 λt  λt  2 λt  λt 2
=e +4e (1 - e ) + 6 e (1 - e ) parallel system with equal number of active units.
(Conditions?).
For t = 0.5 years, t = 0.1 x 0.5 = 0.05 Rs(0.5) = 0.9996

For t = 5 years, t = 0.1 x 5 = 0.5 Rs(5) = 0.8282

50

STANDBY MODELS STANDBY MODELS: MISSILE SYSTEM



13

01-02-2012

System Modelling System Modelling
Two Unit Standby Model Two Unit Standby Model
Obviously, from the Fig (b), it
can be seen easily that the Therefore, reliability for a two-unit standby
system success would be system would be obtained as:

obtained:
Either (i) when the primary unit #
Rs ( t )  Pr[(t1  t) {(t1  t) ( t 2  t  t1 )} ]
1 continues to work beyond or t
the mission time t, i.e., t1 > t,  p 1 t   f 1 t 1  p 2 t  t 1 dt 1
where t1 is the time to failure 0
of unit # 1.
or (ii) unit # 1 fails at time t1 (t1< p1 t   e  1t f 1 t1   1e  1t1 p 2 t  t1   e  2 t t1 
t), and the standby unit ( unit
# 2) comes into operation t
immediately upon the failure R s t   R 1   R 2  e  1t   1 e
 1t
 e   2 t  t1 dt 1
of unit #1 and continues to 0
work for t2 > (t-t1). The system reliability  e 1t e  2 t 
therefore can be given Rs t   e 1t  1  
by:  2  1  1  2 

Rs ( t )  Pr[(t1  t){(t1  t)( t2  t  t1 )}] Indian Institute of Technology, Kharagpur Indian Institute of Technology, Kharagpur

STANDBY MODELS: IMPERFECT SWITCH STANDBY MODELS: OTHER

 The function of decision switch (DS) is critical and the  DS perfect but Degradation of standby unit
success of a standby system to great extent depends in standby mode.
upon the reliability of this decision switch.  Combining degradation of standby unit and


Imperfect switching
 The reliability decision switch is driving the system
reliability.
 Two-unit standby system ,

Rs (t )  P[(t1  t )  {(t1  t )  (t ds  t1 )  (t 2  t  t1 )}]
t
R S ( t )  p 1 ( t )  p ds 
0
f 1 ( t 1 ) p 2 ( t  t1 ) dt 1

tds represents a random variable denoting the time to
failure of the decision switch.

55 56

14

01-02-2012

System Modelling PARTIAL STANDBY MODEL

THREE-UNIT STANDBY MODEL  As shown in fig. there is another way to configure three
units.
 Two units are in operational mode and third unit may
Similarly, we can determine the reliability of be put in standby mode.

a three unit system as:  Actually both units are required in operational mode for
satisfactory operation of the system.
 e  1t e  2t   Thus are in series as far as reliability logic diagram
R s t   e  1t  1   concerned.
  2  1  1   2 
  Third unit replaces any one failed from these two
 e 1t e  2 t e 3t  operational units.
 12    1
 2  1 3  1  1  2 3  2  1  3 2  3 

2

3

Units 1 and 2 are in active mode and unit 3 is in standby mode
58

Standby Models Triple Modular
m1
Redundancy
(t ) i



Rs(t) = e-2( 1+ 2  t ) Rs  exp(t )
i 0 i!

The triple modular redundancy (TMR) consists of three
parallel digital circuits – A, B, and C - all having the same
input. The outputs of the three circuits are compared by a
voter, which sides with the majority and gives the majority
opinion as the system output. If all three circuits are
operating properly, all outputs agree; thus the system output
i t

15

01-02-2012

Triple Modular SHARED LOAD MODEL
Redundancy
However, if one element has failed so that it has produced an  A model in which the load on a member
incorrect output, the voter chooses the output of the two changes and consequently the hazard rate of

good elements as the system output because they both the member also changes, as one or more
agree; thus the system output is correct. If two elements have member fail.
failed, the voter agrees with the majority (the two that have  In this model all the units/sub-systems are
failed); thus the system output is incorrect. The system connected in parallel and each unit shares the
output is also incorrect if all three circuits have failed. load equally.
Actually, circuits-A, B, and C- in most cases are identical and  After the failure of one or more units the
they are three replications of the same design. Using this remaining units share the load equally but with
assumption, and also assuming that the voter does not fail a higher value of hazard rate.
and all digital circuits are independent and identical with  The levels of hazard rate change only when a
probability of success p,3the system reliability is given by: subsystem failure occurs.
R s    p 3 1  p     p 2 1  p   3 p  2 p  p 3  2 p
 3
0   1 2 3 2
 It is assumed that failure distribution of the
3 2 survivor subsystem after failure of a
subsystem does not depend on the interval of

TWO UNIT SHARED LOAD MODEL TWO UNIT SHARED LOAD MODEL

In this case, we will have two units sharing the Let,


given load equally however if one unit fails, the fh(t) : be the p.d.f. for time to failure of a unit
total load will have to be take over by the single under half load condition
unit as shown in the following figure. ff(t) : be the p.d.f. for time to failure of a unit
under full load condition( this occurs
Half load
when one unit fails and other unit is forced
to take the full load )
Half load
Therefore the system is successful if,
1. Both component remain operational until the
mission time. The probability of this is given
Full load by:
P[(t1>t)∩(t2>t)] = {ph(t)}2
Where, ph(t) is reliability of a unit under half
Indian Institute of Technology, Kharagpur load Indian Institute of Technology, Kharagpur

16

01-02-2012

TWO UNIT SHARED LOAD MODEL TWO UNIT SHARED LOAD MODEL
2. The first unit fails and the second unit survives and Now the system reliability is found by adding the

the takes the full load (after the failure of the first probabilities of case 1 , case 2 and case 3 i.e.
unit) until the time t, The probability of this
operation is given by:

P[(t1≤t, under half load)∩(t2>t1, under half load)∩ If we assume the failure distribution to the
exponential distribution for both the units and
( t2>t-t1, under full load)] = denote the failure rates at half and full load by λh
and λf respectively. Then the reliability expression
3. This is identical to the case 2 the only difference is can be written as,  t
2 h e f
R s t   e  2  h t 
that here unit 2 fails and unit 1 take the full load(
after failure of the second unit) and the probability [1  e  ( 2  h   f ) t ]
of this operation can be found by replacing t1 by t2 . (2 h   f )
Incase both the units are same the probabilities
in case 2 and case 3 turns out to Institute of Technology, Kharagpur
Indian
be same. Indian Institute of Technology, Kharagpur

THREE UNIT SHARED LOAD THREE UNIT SHARED LOAD
SYSTEMS SYSTEMS
Similarly the reliability expression for the three The diagrammatic representation of the load


unit shared load model can be derived, the shifting is shown below,
1/3 load
success probability versus time plot is shown
below, #1
Su
E1∩E2∩E3
1/3 load
cce #2 E1∩E2∩E3 

ss E 1  E 2  E3
1/3 load
E1∩E2∩E3 
Pro #3 E1 E 2  E 3
 
ba E1  E 2  E 3 1/2 load
bili
ty 1/2 load
t1 t2
Time t
Full load


17

01-02-2012

SYSTEMS SYSTEMS
For three similar units the above possibilities P(#2) = 3P[(t1≤t,at 1/3 load)∩{(t2>t1) ∩(t3>t1), at 1/3

can be described as, load}∩ {(t2>t-t1) ∩(t3>t-t1), at ½ load}]
1. All the three units operate until the mission And
time and share the load equally. P(#3) = 6P[(t1≤t, at 1/3 load) ∩{(t2>t1) ∩(t3>t1), at 1/3
2. Unit #1 fails and the other two units survive }
load}
and share the load equally. ∩{(t2≤t, at ½ load) ∩(t3>t2, at ½ load)} ∩
3. Unit #1 and Unit #2 fail and Unit #3 operates {(t3>t-t1-t2), at full load}
Now the reliability expression for the three unit shared load model can
and is forced to take the full load. be written as,
Let t1, t2 and t3 be the time to failure of the Rs(t) = P(#1) + P(#2) + P(#)
first, second and third unit respectively then
the probabilities of the above possibilities can
be written as,
P(#1) = P[(t1>t)∩(t2>t) ∩(t3>t)] = [po(t)]3

SYSTEMS SYSTEMS
In the integral form it can be written as, The expression comes out to be,


t

Rs(t) = [po(t)]3 + 3 f o t 1 { p o t 1 } { p h ( t  t 1 )} dt 1

2 2
3o
+ 0 Rs (t)  e3ot  (e3ot  e2ht ) 
t t  t1
(2h 3o )
6  f o t 1 { p o t 1 } 2 f h ( t 2 ) p h ( t 2 )p f ( t  t 1  t 2 )dt 2 dt 1
0 0
e3ot e2ht
Now if we take the failure distribution to be 6oh[  
exponential distribution with failure rates λo, λh (3o  2h )(3o  f ) (2h 3o )(2h  f )
and λf for the 1/3, ½ and full load respectively then
 t
the reliability expression can be written as, e f
]
(f 3o )(f  2h ) Indian Institute of Technology, Kharagpur

18

01-02-2012

System Modelling COMPARISON OF DIFFERENT MODELS
THREE UNIT SHARED LOAD
• Basis:
SYSTEMS
One very important thing to note is that, – Assuming constant failure rate.

• If we put, λ1=2λh and λ2= λf in the two unit – All elements or subsystems are identical with
standby reliability expression we get the reliability, p.
reliability expression for the two unit
shared load model.
h dl d d l
• Similarly if we put λ1=3λo, λ2=2λh and λ3=
λf in three unit standby reliability
expression we will end up with the
reliability expression of three unit shared
load model.
Finally MTTF can be found by
integrating the reliability of Technology, Kharagpur
Indian Institute
expression 74
between 0 and Infinity

SINGLE COMPONENT Three Component in S & P
1 1

1 0.9 0.9

0.9


0.8 0.8
0.8 0.7 0.7
0.7
0.6 0.6
0.6
0.5 0.5
R

R

0.5
R

0.4 0.4
0.4
0.3 0.3
0.3
0.2 0.2
0.2

0.1 Series 0.1
0.1 Series
parallel
0 0 0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p p p

75 76

19

01-02-2012

SP:(2-IN-P WITH 1-IN-S) PS:(2-IN-S WITH 1-P)
1 1

0.9 0.9

0.8 0.8

0.7 0.7

0.6 0.6

0.5
05 0.5
05

R
R

0.4 0.4

0.3 0.3

0.2 Series
0.2
parallel
Series
0.1 SP
0.1 parallel PS
SP
0
0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p
p

77 78

STANDBY WITH ONE ACTIVE AND 2-STNDBY, DS PERFECT, NO
2-OUT-OF-3:G DEGRADATION

1
1
0.9
0.9
0.8


0.8
0.7
0.7
0.6
0.6

0.5
05
R

0.5
R

0.4
0.4

0.3 0.3 Series
parallel
Series
0.2 0.2 SP
parallel
PS
SP
0.1 0.1 2O3:G
PS
2O3:G
Stndby
0 0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p p

79 80

20

01-02-2012

WITH DS HAS HALF THE FR OF UNITS’ FR, NO DEGRADATION
With DS has same FR of units’ FR, No Degradation

1
1
0.9
0.9
0.8

0.8
0.7
0.7
0.6
0.6
0.5
05
R

0.5

R
0.4 Series
parallel 0.4 Series
0.3 SP parallel
PS
0.3 SP
0.2 2O3:G PS
0.2 2O3:G
Stndby
0.1 Stndby
StndbyDSFRH
0.1 StndbyDSFRH
0 StndbyDSFRF
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0
p 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p
81 82

PARTIAL STANDBY Comparison of Various Models

1

0.9


0.8

0.7

0.6

0.5
05
R

Series
0.4 parallel
SP
0.3 PS
2O3:G
0.2 Stndby
StndbyDSFRH
0.1
StndbyDSFRF
Pstndby
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
p

83

21

01-02-2012

COMPARISON OF DIFFERENT MODELS COMPARISON OF DIFFERENT MODELS

• Series and standby provides the lowest and highest bounding curves. • Although, standby model offers best possible reliability. However, in
• Reliability of partial standby and k-out-of-m for some values of p reality it may not be possible to introduce this kind of redundancy with
(0<=p<=0.5) lie below the single component curve line and for higher all types of subsystems or elements.

values of p lie above the single component line. • Besides, the advantage will level off if DS is imperfect and has high
• This implies that reliability of such model is worse than the reliability FR.
of single component for some values of p close to 0 while same models • SO BE CAREFUL IN DESIGNING A SYSTEMS.
offers better reliability for higher values of p.
• SP/PS also would also exhibit similar characteristics for higher order
systems.
• k-out-of-m system invariably shows this characteristic.
• Therefore, it is necessary to know the breakeven point for which a
multi-component system has the same reliability as that of a single
component.
• The designer must ensure that the reliability of his system is better than
this breakeven value while designing.

85 86

SHARED LOAD MODEL

 This model is considered in which load on a member changes and
consequently the hazard rate of the member changes, as one or more  If any one fails the remaining two will share the load of 100MW each
members fail. to meet requirement , obviously now failure rate of the surviving
generator s will be higher than before.


 In this model all the units or subsystem comprising the system are
connected in parallel and each unit shares the load equally.  Therefore in this model the levels of hazard rate changes only when a
subsystem failure occurs.
 If any of subsystem fails the surviving subsystems will share the load
fails,
equally but with higher value of hazard rate.

 For example,
If three generators of 110MW each, connected in parallel electricity and
the load is 200MW, then each of these generators shares a load of
66.67MW and at this load each generator has definite failure rate.

87 88

22

01-02-2012

 The system will be good if:
 Two units shared load Model:
Two units are sharing given
load equally. However if a unit 1. Both components remain in operational mode until the mission
fails, the total load will have to be E1∩E2 time.

#1
taken over by a single unit.
Success E1∩E2
probabilities
The probability of this given by,
E1∩E2
#2
P[t1>t∩t2>t]={ph (t)}2
Let (t) be h d f for
L fh( ) b the p.d.f. f t1 t
time to failure of a unit under half Time Where, ph (t) is reliability of a unit at half load condition
load condition. i.e. 
Success probabilities of two unit
shared load system p h (t )  
t
f h ( u ) du

Let ff(t)be the p.d.f. for time t1 and t2 are time to failure of two units and the ‘t’ is mission time.
to failure of a unit under full load
condition.

89 90

3 This is like 2 but instead of the first unit failing fist, the second
unit is fails first and the other survives until time t.
2 Unit 1 is failed at time t1 , and prior to this the units are taking
half of the load each. After time t1 ,unit 2 alone takes the full


load until time t. the probability of this operation
the probability of this operation ,
P[(t 2  t , under half load )  (t1  t 2 , under half load ) 
P[( t1  t , under half load )  (t 2  t1 , under half load )  (t1  t  t 2 , under full load )]
( t 2  t  t1 , under full load )] t
  f h (t 2 ) ph (t 2 ) p f (t  t 2 ) dt 2
t
0
  f h (t1 ) ph (t1 ) p f (t  t1 ) dt1
0 System Reliability = [ sum of the probabilities of earlier three
 equations]
where p f (t )   f f (u ) d (u ) t
t
RS  [ ph (t )]2  2 f h (t1 ) ph (t1 ) p f (t  t1 ) dt1
0
91 92

23

01-02-2012


93

24

3. reliability modelling

More Related Content

Similar to 3. reliability modelling

Recently uploaded

3. reliability modelling