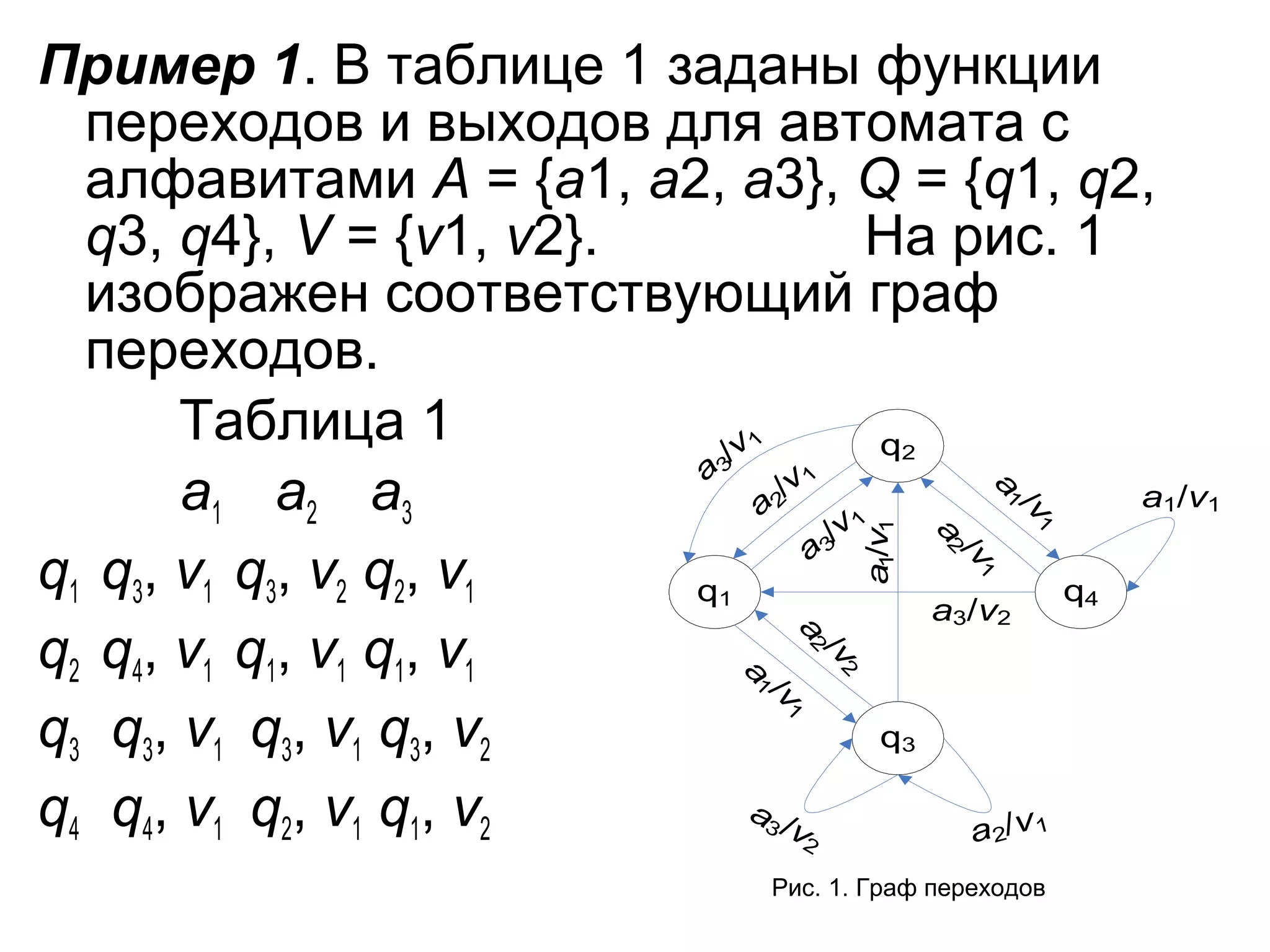
Документ посвящен теории автоматов и описывает конечные автоматы и машины Тьюринга, включая их структуру и функциональность. В нем объясняются ключевые понятия, такие как входные и выходные алфавиты, функции переходов и выходов, а также представление автоматов в виде таблиц и графов. Также рассматриваются основные аспекты работы автоматов, такие как распознавание и преобразование входных слов.

1. Теория автоматов
1. Конечные автоматы

2. Конечным автоматом (далее – автоматом)
называется система S = {A, Q, V, δ, λ}, в
которой A = {a1, …, am}, Q = {q1, …, qn}, V = {v1, …,
vk} – конечные множества (алфавиты), а δ: Q ×
A → Q и λ: Q × A → V – функции, определенные
на этих множествах. A называется входным
алфавитом, V – выходным алфавитом, Q –
алфавитом состояний, δ – функцией
переходов, λ – функцией выходов. Если,
кроме того, в автомате S выделено одно
состояние, называемое начальным, то
полученный автомат называется инициальным
и обозначается (S, q). Таким образом, по
неинициальному автомату с n состояниями
можно n способами определить инициальный
автомат.

3. Поскольку функции δ и λ определены на конечных
множествах, их можно задавать таблицами. Обычно
две таблицы сводятся в одну таблицу δ × λ: Q × A
→ Q × V, называемую таблицей переходов автомата
или просто автоматной таблицей.
Еще один распространенный и наглядный способ
задания автомата – ориентированный мультиграф,
называемый графом переходов или диаграммой
переходов; если δ(qi, aj) = qk и λ(qi, aj) = vl, то из qi в qk
ведет ребро, на котором написаны aj и vl. Для любого
графа переходов в каждой вершине qi выполнены
следующие условия, которые называются
условиями автоматности: 1) для любой входной
буквы aj имеется ребро, выходящее из qi (условие
полноты); 2) любая буква aj встречается только на
одном ребре, выходящем из qi (условие
непротиворечивости или детерминированности).

4. 1
Пример 1. В таблице 1 заданы функции
переходов и выходов для автомата с
алфавитами A = {a1, a2, a3}, Q = {q1, q2,
q3, q4}, V = {v1, v2}.
На рис. 1
изображен соответствующий граф
переходов.
Таблица 1
q
a /v
a1 a2 a3
q1 q3, v1 q3, v2 q2, v1
q
q
a /v
q2 q4, v1 q1, v1 q1, v1
q3 q3, v1 q3, v1 q3, v2
q
a/
q4 q4, v1 q2, v1 q1, v2
v
a /v
a1/v1
3/
a
1
4
2
1
/v
a1
2
/v
a2
3
3
3
2
1
1
/v
a2
v
1
a
2/
1
/v
a1
v
1
a
3/
v
2
2
1
Рис. 1. Граф переходов
1

5. Для данного автомата S его функции δS и λS могут
быть определены не только на множестве A всех
входных букв, но и на множестве A* всех
входных слов. Для любого входного слова α =
aj1aj2…ajk δ(qi, aj1aj2…ajk) = δ(δ(… δ(δ(qi, aj1), aj2), …, ajk –
1), ajk).
Также данное определение можно выразить
индуктивно:
1) δ(qi, aj) задается автоматной таблицей S;
2) для любого слова α ∈ A* и любой буквы aj
δ(qi, αaj) = δ(δ(qi, α), aj).
С помощью расширенной функции δ определяется
(также индуктивно) расширенная функция λ: λ(qi,

6. Соответствие, отображающее входные слова в
выходные слова, называется автоматным
отображением, а также автоматным (или
ограниченно-детерминированным) оператором,
реализуемым автоматом (S, q1) с начальным
состоянием q1. Иногда говорят кратко – оператор
(S, q1) или оператор S (если автомат S –
инициальный). Если результатом применения
оператора к слову α является выходное слово ω,
то это обозначают соответственно (S, q1) = ω или
S(α) = ω. Число букв в слове α называется
длиной α и обозначается |α|. Автоматное
отображение также можно определить
индуктивно:
S(qi, aj) = λ(qi, aj); S(qi, αaj) = S(qi, α)λ(δ(qi, α), aj).

7. Автоматное отображение обладает двумя
свойствами:
1) слова α и ω = S(α) имеют одинаковую длину: |α|
= |ω| (свойство сохранения длины);
2) если α = α1α2 и S(α1α2) = ω1ω2, где |α1| = |ω1|, то S(α1)
= ω1 (образ отрезка i равен отрезку образа той же
длины).
Введенные определения наглядно
интерпретируются на графе переходов. Если
зафиксирована вершина qi, то всякое слово α =
ai1ai2…aik однозначно определяет путь (qi, α)
длины k из этой вершины, на k ребрах которого
написаны соответственно буквы ai1, ai2, …, aik.
Поэтому δ(qi, α) – это последняя вершина пути
(qi, α), λ (qi, α) – выходная буква, написанная на
последнем ребре пути (qi, α), а отображение S(qi,
α) – слово, образованное k выходными буквами,

8. Состояние qi называется достижимым из состояния qi,
если существует входное слово α такое, что δ(qi, α) =
qi. Автомат S называется сильно связным, если из
любого его состояния достижимо любое другое
состояние.
Автомат называется автономным, если его входной
алфавит состоит из одной буквы: A = {a}. Все
входные слова автономного автомата имеют вид
aa…a.
При подходе к теории автоматов как к части теории
алгоритмов центральной проблемой является
изучение возможностей автоматов в терминах
множеств слов, с которыми работают автоматы.
Можно выделить два основных аспекта «работы»
автоматов: 1) автоматы распознают входные слова,
т. е. отвечают на вопрос, принадлежит ли поданное
на вход слово данному множеству; 2) автоматы
преобразуют входные слова в выходные, т. е.
реализуют автоматные отображения.

9. 2. Машины Тьюринга
Машина Тьюринга – это гипотетическая машина, которая
состоит из:
1) управляющего устройства, которое может находиться в
одном из состояний, образующих конечное множество Q =
{q1, …, qn},
2) ленты, разбитой на ячейки, в каждой из которых может быть
записан один из символов конечного алфавита A = {a1, …,
am},
3) устройства обращения к ленте – считывающей и пишущей
головки, которая в каждый момент времени обозревает
ячейку ленты, в зависимости от символа в этой ячейке и
состояния управляющего устройства записывает в ячейку
символ (быть может, совпадающий с прежним или пустой, т.
е. стирает символ), сдвигается на ячейку влево или вправо
или остается на месте; при этом управляющее устройство
переходит в новое состояние (или остается в старом). Среди
состояний управляющего устройства выделены начальное и
заключительное состояния. В начальном состоянии машина
находится перед началом работы; попав в заключительное
состояние машина останавливается.

10. Данные машины Тьюринга – это слова в
алфавите ленты; на ленте записываются и
исходные данные, и окончательные результаты.
Элементарные шаги машины – это считывание
и запись символов, сдвиг головки на ячейку
влево и вправо, а также переход управляющего
устройства в следующее состояние.
Задание машины Тьюринга может описываться
либо системой правил (команд) вида qiaj →
qkaldr, либо таблицей, строкам которой
соответствуют состояния, столбцам – входные
символы, а на пересечении строки qi и столбца
aj записана тройка символов qkaldr, и, наконец,
блок-схемой, которую называют диаграммой
переходов. В диаграмме переходов состояниям
соответствуют вершины, а правилу – ребро,
ведущее из qi в qk, на котором написано aj → aldr.

11. Детерминированность машины, т. е. последовательность ее
шагов, определяется следующим образом: для любого
внутреннего состояния qi и символа aj однозначно заданы
следующее состояние qk, символ al, который нужно записать
вместо aj в ту же ячейку (стирание символа понимается как
запись пустого символа), направление сдвига головки dr,
обозначаемое одним из трех символов: L (влево), R
(вправо), E (на месте).
Полное состояние машины Тьюринга, по которому однозначно
можно определить ее дальнейшее поведение, определяется
ее внутренним состоянием, состоянием ленты (т. е. словом,
записанным на ленте) и положением головки на ленте.
Полное состояние называется конфигурацией и
обозначается тройкой α1qiα2, где α1 – слово слева от головки,
а α2 – слово, образованное символом, обозреваемым
головкой, и символами справа от него, причем слева от α1 и
справа от α2 нет непустых символов. Стандартной
начальной конфигурацией называется конфигурация вида
q1α, где q1 – начальное состояние. Стандартной
заключительной конфигурацией называется конфигурация
вида qZα, где qZ – заключительное состояние.