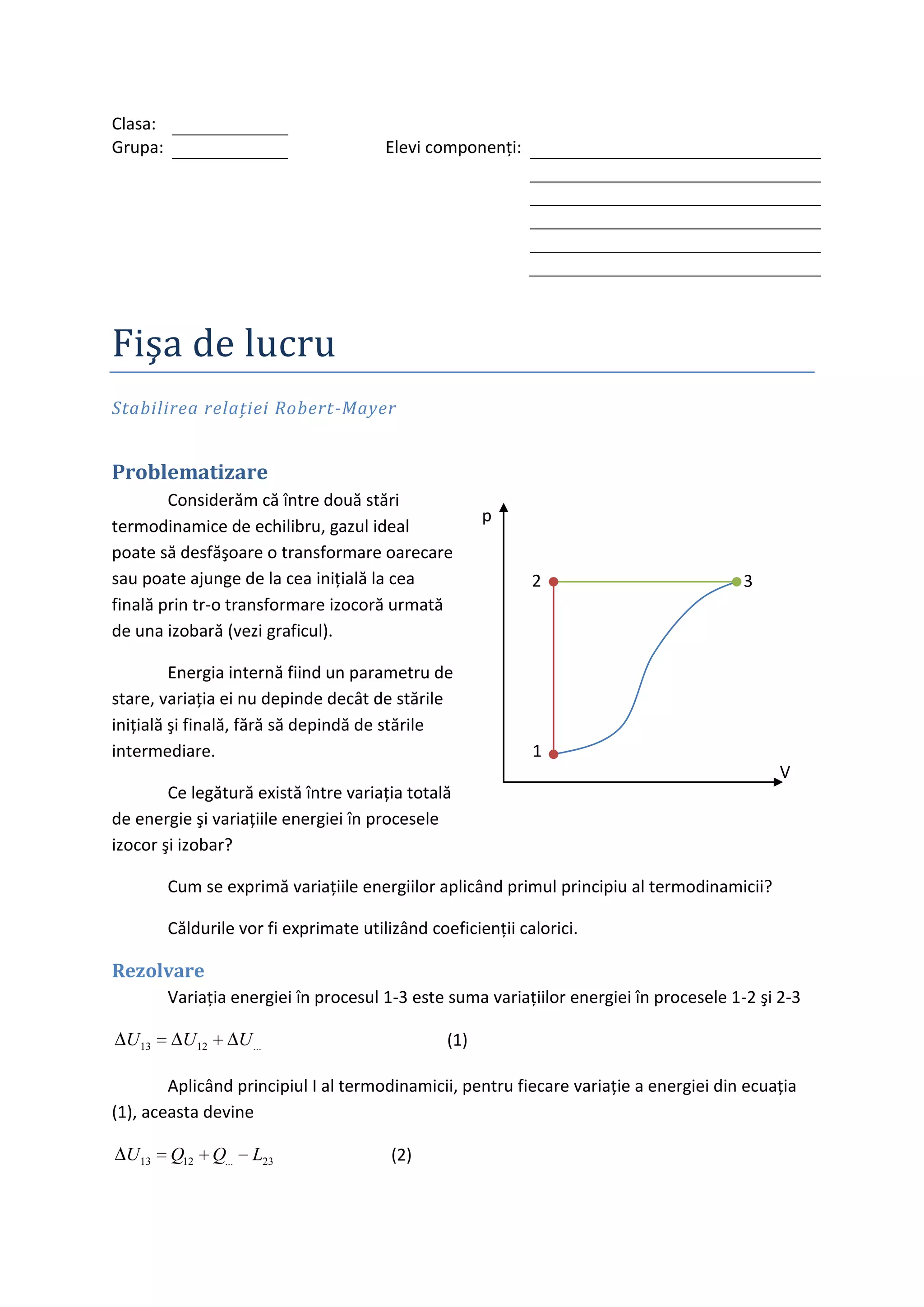
Documentul analizează relația Robert-Mayer în termodinamică, care descrie legătura dintre capabilitățile calorice ale gazelor ideale. Se explică modul în care variațiile energiei pentru procesele izocore și izobare contribuie la variația totală a energiei între două stări de echilibru. Relația finală arată că cp - cv = r pentru un mol de gaz ideal.

1. Clasa:
Grupa: Elevi componenţi:
Fişa de lucru
Stabilirea relaţiei Robert-Mayer
Problematizare
Considerăm că între două stări
p
termodinamice de echilibru, gazul ideal
poate să desfăşoare o transformare oarecare
sau poate ajunge de la cea iniţială la cea 2 3
finală prin tr-o transformare izocoră urmată
de una izobară (vezi graficul).
Energia internă fiind un parametru de
stare, variaţia ei nu depinde decât de stările
iniţială şi finală, fără să depindă de stările
intermediare. 1
V
Ce legătură există între variaţia totală
de energie şi variaţiile energiei în procesele
izocor şi izobar?
Cum se exprimă variaţiile energiilor aplicând primul principiu al termodinamicii?
Căldurile vor fi exprimate utilizând coeficienţii calorici.
Rezolvare
Variaţia energiei în procesul 1-3 este suma variaţiilor energiei în procesele 1-2 şi 2-3
U 13 U 12 U ... (1)
Aplicând principiul I al termodinamicii, pentru fiecare variaţie a energiei din ecuaţia
(1), aceasta devine
U 13 Q12 Q... L23 (2)

2. Aplicând ecuaţia calorică de stare şi definiţia capacităţii calorice molare, termenii
ecuaţiei (2) se scriu astfel:
U13 CV T13
Q12 C... T12
(3)
Q23 C p T23
L23 p V... R T23
Dacă se înlocuiesc termenii ecuaţiei (2) utilizând ecuaţiile (3) şi se rearanjează
termenii ecuaţiei obţinute, avem:
CV T3 T1 T2 T1 Cp ... T23 (4)
Adică
C... T23 Cp ... T23 (5)
Simplificând prin ΔT23, şi rearanjând, se obţine
Cp CV R (6)
adică relaţia Robert-Mayer pentru un mol de gaz ideal.
Evident că pentru un număr oarecare de moli de gaz ideal relaţia Robert-Mayer se
scrie astfel:
Cp CV R