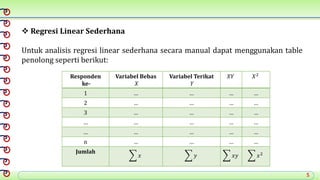
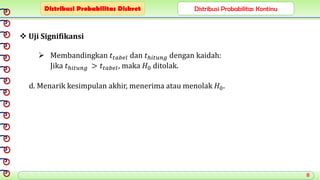
Dokumen ini membahas analisis regresi yang mempelajari hubungan statistik antara variabel bebas dan variabel terikat serta cara meramalkan nilai variabel. Terdapat dua jenis analisis regresi: regresi linear sederhana dan regresi linear berganda, masing-masing menggunakan satu dan beberapa variabel bebas. Selain itu, dijelaskan juga tentang langkah-langkah untuk membuat persamaan regresi serta uji signifikansi untuk menentukan hubungan yang signifikan antara variabel.

1. REGRESI

2. 2
 Analisis Regresi
 Mempelajari dan mengukur hub statistik yg tjd antara 2 variabel atau lebih.
 Meramalkan/ memperkirakan nilai dari satu variabel dalam hubungannya
dgn variabel lain yg diketahui melalui persamaan regresi.
 Teknik statistika yg berguna utk memeriksa dan memodelkan hub diantara
var (terapannya biasanya dikaitkan dengan studi ketergantungan suatu
variabel bebas pada variabel terikat)
 Variabel bebas
Adalah variable yang tidak dipengaruhi oleh variable lain.
 Variabel terikat
Adalah variable yang dipengaruhi oleh variable lain.

3. 3
 Analisis Regresi
 Regresi Linear Sederhana
 Regresi Linear Berganda
 Regresi Linear Sederhana
Adalah analisis regresi yang dilakukan dengan satu variabel terikat (dependent)
dan satu variabel bebas (independent)
 Regresi Linear Berganda
Adalah analisis regresi yang dilakukan dengan satu variabel terikat (dependent)
dan dua atau lebih variabel bebas (independent)

4. 4
 Regresi Linear Sederhana
Dirumuskan dengan :
𝑌 = 𝑎 + 𝑏𝑋
Dimana:
𝑎 & 𝑏 : Konstanta
𝑋 : Variabel bebas
𝑌 : variabel terikat

5. 5
 Regresi Linear Sederhana
Untuk analisis regresi linear sederhana secara manual dapat menggunakan table
penolong seperti berikut:
Responden
ke-
Variabel Bebas
𝑋
Variabel Terikat
𝑌
𝑋𝑌 𝑋2
1 … … … …
2 … … … …
3 … … … …
… … … … …
… … … … …
n … … … …
Jumlah
𝑥 𝑦 𝑥𝑦 𝑥2

6. 6
 Regresi Linear Sederhana
Membuat persamaan regresi dapat dilakukan dengan langkah-langkah
a. Membuat table penolong.
b. Menghitung nilai konstanta 𝑎 & 𝑏, dimana:
𝑏 =
𝑛 𝑥𝑦 − 𝑥 𝑦
𝑛 𝑥2 − 𝑥 2
Dan
𝑎 =
𝑦 − 𝑏 𝑥
𝑛
c. Membuat persamaan regresi

7. 7
 Uji Signifikansi
a. Membuat Hipotesis
 𝐻0 ∶ 𝛼 = 0 Tidak terdapat pengaruh yang signifikan X terhadap Y
 𝐻1 ∶ 𝛼 ≠ 0 Terdapat hubungan pengaruh yang signifikan X terhadap Y
b. Menentukan resiko kesalahan atau taraf signifikansi (𝛼)
c. Uji Hipotesis
 Menghitung nilai 𝑡ℎ𝑖𝑡𝑢𝑛𝑔 dengan:
𝑡ℎ𝑖𝑡𝑢𝑛𝑔 =
𝑟 𝑛 − 2
1 − 𝑟2
 Menentukan 𝑡𝑡𝑎𝑏𝑒𝑙 (𝛼, 𝑛 − 2)

8. 8
 Uji Signifikansi
 Membandingkan 𝑡𝑡𝑎𝑏𝑒𝑙 dan 𝑡ℎ𝑖𝑡𝑢𝑛𝑔 dengan kaidah:
Jika 𝑡ℎ𝑖𝑡𝑢𝑛𝑔 > 𝑡𝑡𝑎𝑏𝑒𝑙, maka 𝐻0 ditolak.
d. Menarik kesimpulan akhir, menerima atau menolak 𝐻0.
Distribusi Probabilitas Diskret Distribusi Probabilitas Kontinu

9. 9
Contoh :
Seorang mhs jurusan agribisnis ingin mengetahui apakah ada hubungan pengaruh
antara biaya iklan perusahaan (X) dgn tingkat laba bersih perusahaan (Y), semua
biaya dalam jutaan rupiah.
a. Hitung korelasi antara X dan Y!
b. Berapa besar variabel X berkontribusi terhadap Y?
c. Gunakan taraf signifikansi 5 %, ujilah apakah ada hubungan yang signifikan
antara biaya iklan perusahaan (X) dgn tingkat laba bersih perusahaan (Y)!
d. Bagaimana persamaan regresinya!
X 1,5 1,0 2,8 0,4 1,3 2,0
Y 3,6 2,8 5,4 1,9 2,9 4,3

10. Semoga Bermanfaat!!!!
Terima kasih