01VD062009003760042.pdf

Unit I
SE Computer Engineering
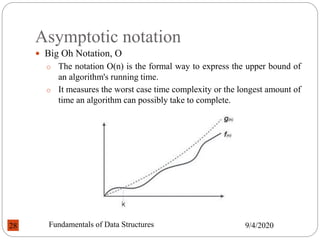
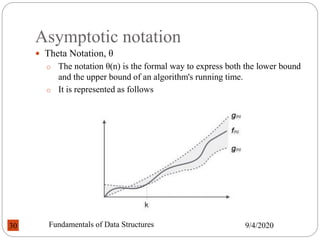
Introduction to Algorithm and Data
Structures
9/4/2020
Fundamentals of Data Structures
1

Outline
 Introduction:
 Data Structures:
 Algorithms:
 Algorithm design tools:
 Complexity of algorithm:
 Algorithmic Strategies:
9/4/2020
2

Course Outcomes
 CO1: Design the algorithms to solve the programming problems, identify
appropriate algorithmic strategy for specific application, and analyze the
time and space complexity.
 CO2: Discriminate the usage of various structures,
Design/Program/Implement the appropriate data structures; use them in
implementation of abstract data types and Identity the appropriate data
structure in approaching the problem solution.
 CO3: Demonstrate use of sequential data structures- Array and Linked lists
to store and process data.
 CO4: Understand the computational efficiency of the principal algorithms
for searching and sorting and choose the most efficient one for the
application.
 CO5: Compare and contrast different implementations of data structures
(dynamic and static).
 CO6: Understand, Implement and apply principles of data structures-stack
and queue to solve computational problems.
9/4/2020
3

From Problem to Program
 It is noticed that programmers spend most of their time in
understanding what problems to solve. Initially, most problems
have no simple, precise specifications.
 If certain aspects of a problem can be expressed in terms of a
formal model, it is usually beneficial to do so, for once a
problem is formalized, we can look for solutions in terms of a
precise model and determine whether a program already exists to
solve that problem.
 Even if there is no existing program, we can at least discover
what is known about this model and use the properties of the
model to help construct a good solution.
9/4/2020
4

Problem Solving
 Problem Solving is the process in which Programmers
must first understand how a human solves a problem, then
understand how to translate this "algorithm" into something
a computer can do, and finally how to "write" the specific
syntax (required by a computer) to get the job done.
9/4/2020
5
Problem
(Solving)
Algorithm
Computer
Input Output
Program

Data, Data Type & Data Structure
 Data is nothing but a piece of information.
 Data Type
o Data type refers to the kind of data a variable may store.
o Built-in Data Types- int, float, and char are built-in data types.
o User-defined Data Types-structures, unions, and classes.
 Data Structure
o Data structures refer to data and representation of data objects within a
program, that is, the implementation of structured relationships
9/4/2020
6

Abstract Data Types
 Typical operations on data
o Add data to a data collection
o Remove data from a data collection
o Ask questions about the data in a data collection
 Data abstraction
o Asks you to think what you can do to a collection of data
independently of how you do it
o Allows you to develop each data structure in relative isolation from
the rest of the solution
9/4/2020
7

Abstract Data Types
 An abstract data type (ADT) is composed of
o A collection of data
o A set of operations on that data
 Specifications of an ADT indicate what the ADT operations do
(but not how to implement them)
 Implementation of an ADT includes choosing a particular data
structure
9/4/2020
8

Type of Data Structures
 Data Structure - a way of organizing data that specifies
o a set of data elements, that is, a data object; and
o a set of operations that are applied to this data object.
 The data structure is independent of their implementation. The
various types of data structures are as follows:
o primitive and non-primitive
o linear and non-linear
o static and dynamic
o persistent and ephemeral
9/4/2020
9

 Primitive
o Primitive data structures define a set of primitive elements that do
not involve any other elements as its subparts — for example, data
structures defined for integers and characters.
o These are generally primary or built-in data types in programming
languages.
 Non-Primitive
o Non-primitive data structures are those that define a set of derived
elements such as arrays. Arrays in C++ consist of a set of similar
type of elements.
o Class and structure are other examples of non-primitive data
structures, which consist of a set of elements that may be of
different data types and functions to operate on.
9/4/2020
10

 Linear
o Its elements form a sequence or a linear list.
o Every data element has a unique successor and predecessor.
o One way to represent is to have the relationship between the
elements by means of pointers (links), called linked lists.
o The other way is using sequential organization, that is, arrays.
 Non-linear
o Used to represent the data containing hierarchical or network
relationship among the elements.
o Trees and graphs are examples of non-linear data structures.
o Every data element may have more than one predecessor as well as
successor.
o Elements do not form any particular linear sequence.
9/4/2020
11

 Static
o A data structure is referred to as a static data structure if it is created
before program execution begins.
o The variables of static data structure have user-specified names. An
array is a static data structure.
 Dynamic
o Created at run-time is called dynamic data structure.
o The variables of this type are not always referenced by a user-
defined name.
o These are accessed indirectly using their addresses through
pointers.
o Trees and graphs can be implemented as dynamic data structures.
9/4/2020
12

 Persistent
o The operations that process the data may modify the data. This may
create two versions of a data structure namely the recently modified
and the previous version.
o A data structure that supports operations on the most recent version
as well as the previous version is termed as a persistent data
structure.
o A persistent data structure is partially persistent if any version can
be accessed but only the most recent one can be updated; it is fully
persistent if any version can be both accessed and updated.
 Ephemeral
o An ephemeral data structure is one that supports operations only on
the most recent version.
9/4/2020
13

Algorithms
9/4/2020
15

Algorithms
 Problem Solving
 Introduction to Algorithms,
 Characteristics of algorithms,
 Algorithm design tools:
o Pseudo code and flowchart,
 Analysis of Algorithms,
 Complexity of algorithms-
o Space complexity, Time complexity,
o Asymptotic notation- Big-O, Theta and Omega,
o standard measures of efficiency.
9/4/2020
16

Algorithms
 An algorithm is a finite set of instructions which, if
followed, accomplish a particular task. In addition every
algorithm must satisfy the following criteria:
o input: An algorithm should have 0 or more well-defined inputs;
o output: An algorithm should have 1 or more well-defined outputs,
and should match the desired output;
o definiteness: each instruction must be clear and
unambiguous;
o finiteness: Algorithms must terminate after a finite number of
steps;
o effectiveness: every instruction must be sufficiently basic that it can
in principle be carried out by a person using only pencil and paper.
Each operation must also be feasible.
9/4/2020
17

Algorithm design tools
 Flowchart:
o a diagrammatic representation of sequence of logical steps of
a program.
o Flowcharts use simple geometric shapes to depict processes
and arrows to show relationships and process/data flow.
 Pseudo code:
o an informal high-level description of the operating principle
of a computer program or other algorithm.
o It uses the structural conventions of a normal programming
language,
o but is intended for human reading rather than machine
reading.
9/4/2020
18

Algorithm design tools- Flowchart
9/4/2020
19
Symbol
Symbol
Name
Purpose
Start/Stop
Used at the beginning and end of the algorithm to
show start and end of the program.
Process Indicates processes like mathematical operations.
Input/ Output Used for denoting program inputs and outputs.
Decision
Stands for decision statements in a program,
where answer is usually Yes or No.
Arrow Shows relationships between different shapes.

Algorithm design tools- Flowchart
9/4/2020
20
Declare Variables a, b, c
Read a, b
C <- a + b
Print C (Sum)
Start
Stop

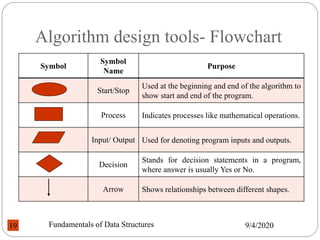
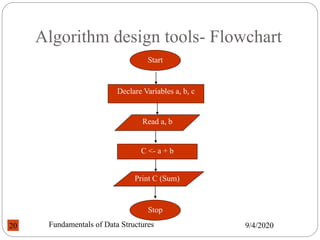
Algorithm design tools
Pseudo code:
9/4/2020
21
 High-level description of
an algorithm.
 More structured than
plain English.
 Less detailed than a
program.
 Preferred notation for
describing algorithms.
Algorithm arrayMax(A, n)
Input array A of n integers
Output maximum element of A
currentMax  A[0]
for i  1 to n  1 do
if A[i]  currentMax then
currentMax  A[i]
return currentMax
Example: find the max element
of an array

Analysis of Algorithms
 There can be several ways to organize data and/or write
algorithms for a given problem.
 We can compare one algorithm with the other and choose
the best. For comparison, we need to analyze the
algorithms. Analysis involves measuring the performance
of an algorithm.
 Performance is measured in terms of the following
parameters:
o Time complexity
o Space complexity
9/4/2020
22

 Time complexity is a function describing the amount of time an
algorithm takes in terms of the amount of input to the algorithm.
 An algorithm can be characterized by a timing function T (n).
 T (n) is a measure of how much time is required to execute an
algorithm with the given n data values.
 For example, the timing function for a sort operation specifies
the time required to sort n data values.
9/4/2020
23

 Space complexity is a function describing the amount of
memory (space) an algorithm takes in terms of the amount of
input to the algorithm.
 We often speak of "extra" memory needed, not counting the
memory needed to store the input itself.
 Space complexity is sometimes ignored because the space used
is minimal and/or obvious, but sometimes it becomes as
important an issue as time.
 Space complexity measurement, which is the space
requirement of an algorithm, can be performed at two different
times:
 Compile time
 Run time
9/4/2020
24

• Compile time space complexity is defined as the storage
requirement of a program at compile time.
• This can be determined by summing up the storage size of each
variable using declaration statements.
• For example, the space complexity of a non-recursive function
of calculating the factorial of number n depends on the number n
itself.
Space complexity = Space needed at compile time
• Run-time Space Complexity: If the program is recursive or
uses dynamic variables or dynamic data structures, then there is
a need to determine space complexity at run-time.
• Memory requirement is summation of Program space, Data space,
Stack space.
9/4/2020
25

Asymptotic notation
 Asymptotic analysis of an algorithm refers to defining the
mathematical boundation/framing of its run-time
performance.
 Using asymptotic analysis, we can very well conclude the
best case, average case, and worst case scenario of an
algorithm.
 For example, the running time of one operation is
computed as f(n) and may be for another operation it is
computed as g(n2).
 This means the first operation running time will increase
linearly with the increase in n and the running time of the
second operation will increase exponentially when n
increases.
9/4/2020
26

Asymptotic notation
 Usually, the time required by an algorithm falls under three
types
o Best Case − Minimum time required for program execution.
o Average Case − Average time required for program
execution.
o Worst Case − Maximum time required for program
execution.
 Following are the commonly used asymptotic notations to
calculate the running time complexity of an algorithm.
o Ο Notation
o Ω Notation
o θ Notation
9/4/2020
27

Asymptotic notation
 Big Oh Notation, Ο
o The notation Ο(n) is the formal way to express the upper bound of
an algorithm's running time.
o It measures the worst case time complexity or the longest amount of
time an algorithm can possibly take to complete.
9/4/2020
28

Asymptotic notation
 Omega Notation, Ω
o The notation Ω(n) is the formal way to express the lower bound of
an algorithm's running time.
o It measures the best case time complexity or the best amount of
time an algorithm can possibly take to complete.
9/4/2020
29

Asymptotic notation
 Theta Notation, θ
o The notation θ(n) is the formal way to express both the lower bound
and the upper bound of an algorithm's running time.
o It is represented as follows
9/4/2020
30

Example
{
for (i=0; i<n; i++)
cout<<“Hello Students”;
}
9/4/2020
32

Algorithmic Strategies
 We have discussed data structures, programming languages,
algorithms, and their analysis. Software development desires to
utilize each of these efficiently.
 The basic programming style is influenced by typical design
approaches called algorithmic strategies. An algorithmic strategy
is a general approach to solving problems algorithmically.
 Devising an algorithm is an art that may never be fully
automated. We shall study various design techniques that have
proven to be useful to devise new algorithms.
 Dynamic programming is one such technique along with others
such as divide-and conquer, greedy, and backtracking. More than
one technique may be applicable to a specific problem.
9/4/2020
34

Algorithmic Strategies- Divide-and-
conquer
 It works in two phases. In the first phase, the problem is divided
into subproblems of smaller size till each problem can be easily
solved. In the latter phase, the solutions to all such subproblems
are gathered together to get the final solution.
 Often, even the subproblems are relatively large, and the divide-
and-conquer strategy is reapplied. In addition, the subproblems
resulting from a divide-and-conquer design are of the same type
as the original problem.
 For those cases, applying this design again is naturally expressed
by a recursive procedure. The process of splitting the input into
distinct subsets continues till these smaller subproblems, are
small enough to be solved without further splitting.
9/4/2020
35

Divide-and-conquer
 Algorithm Divide_and_Conquer(A, lower, upper)
1. start
2. if small(lower, upper) then
return Soln(lower, upper)
3. else Divide A into smaller instances say A1, A2, … Ak
4. for i = 1 to k do
Apply Divide_and_Conquer to Ai
5. return conquer(Divide_and_Conquer(A1)),
Divide_and_Conquer(A2),
…
Divide_and_Conquer(Ak))
6. stop
9/4/2020
36

Divide-and-conquer: Characteristics
and Use
 The following are some unique characteristics of the divide-and-
conquer method:
o The divide-and-conquer technique is well suited when a data set
can be divided into smaller subsets of data elements and each data
set can be independently processed.
o It is useful in cases where algorithms are inherently recursive.
o It is not suitable for data elements that are not suitably subdivided
and if the subtasks cannot be independently processed.
9/4/2020
37

Greedy Method
 A greedy method is any algorithm that follows the problem-
solving heuristic of making the locally optimal choice at each
stage with the hope of finding the optimum solution.
 For example, applying the greedy strategy to the travelling
salesman problem yields the following algorithm: ‘At each stage,
visit the unvisited city nearest to the current city’. In general,
greedy algorithms are used for optimization problems.
 A feasible solution to which the optimization function has the
best possible value is called an optimal solution.
 In greedy method, we attempt to construct an optimal solution in
the sequence of choice. At each choice, we make a decision that
appears to be the best at that time.
9/4/2020
38

Greedy Method
 The greedy algorithm suggests that one can devise an algorithm
that works in stages, considering one input at a time.
 At each stage, a decision is made based on whether or not a
particular input is an optimal solution.
 Any subset of input that satisfies the given constraints is called a
feasible solution.
 A feasible solution that maximizes or minimizes a given
objective is called an optimal solution.
 There is usually an obvious way to determine a feasible solution
but not necessarily an optimal solution.
9/4/2020
39

01VD062009003760042.pdf

More Related Content

Similar to 01VD062009003760042.pdf

Recently uploaded

01VD062009003760042.pdf