Download to read offline
![旭丘数理科学部
旭丘数理科学部
Ants
OPTION BASE 0
LET L, N
DIM X(N)
FOR i = 0 TO N
INPUT X(N)
NEXT N
LET mintT = 0 , maxT = 0
FOR i = 0 TO N
LET minT = max(minT , min(x[i] , L - x[i]) // max(a,b)でa,bの大きい方 min(a,b)でa,bの小さい方
LET maxT = max(maxT , max(x[i], L – x[i])
NEXT I
PRINT minT
PRINT maxT
END](https://image.slidesharecdn.com/0th-211201174829/85/0-35-320.jpg)
Uploaded by旭丘 情報科学
旭丘数理科学部第0回情報
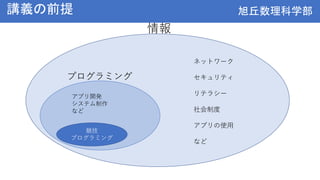
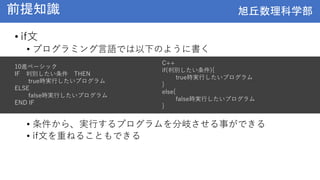
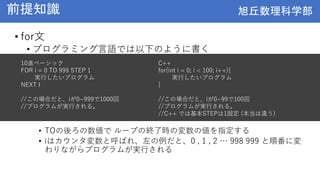
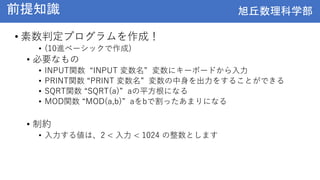
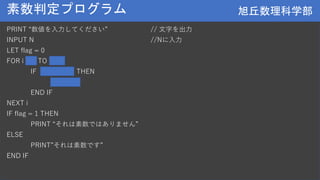
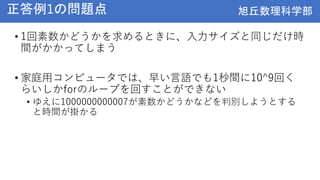
The document discusses an introductory lecture on competitive programming. It outlines some key points: - The goal is to help students become able to win competitive programming contests. - C++ will be the main language covered due to its speed advantages for competitions. - Basic concepts from middle school math like variables, functions, if/for statements will be briefly reviewed. New topics of arrays and computational complexity will also be introduced. - Simplicity and readability will be prioritized over technical accuracy in explanations. Students are encouraged to research topics further online.
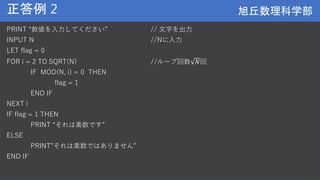
旭丘数理科学部第0回情報
- 1. 旭丘数理科学部 旭丘数理科学部 旭丘数理科学部 情報講義担当 たきかわ @cinnamon_cute_ おしながき 第0回 情報講義 •講義の前提 • 前提知識を復習 • 予備知識の学習 • 実際に問題に触れてみよう！
- 2.
- 3. 旭丘数理科学部 旭丘数理科学部 講義の前提 • 情報講義で目指すもの • 競技プログラミングコンテストで勝てるようになること •AtCoder(国内最大級の競プロコンテストサイト) • JOI(日本情報オリンピック) • PCK(パソコン甲子園) など • ネットワークやアプリ開発など、他の分野は一切触れない • この講義は情報のほんの一部分しか扱わないので、 • あまり全貌を知った気にならないように気をつけてください • 情報というより、競技プログラミングの講義です
- 4.
- 5. 旭丘数理科学部 旭丘数理科学部 講義の前提 • いっぱい書いてますが、全部読まなくていいです • あとから読み返せるように、一応ちょっと細かく書いてます •一応見返したらある程度分かるようになってるはず • 1つのものに頼らずGoogle検索 • 情報の知識はネットに無限に転がってます • 1個の問題に対して10個の解説を見ましょう • たぶん1つくらいあなたに合う解説が世の中にあります
- 6. 旭丘数理科学部 旭丘数理科学部 講義の前提 • 扱う言語 :C++ • 理由 • 動作の速度が早いため、競技プログラミングに向いています • JOIやAtCoderなどの解説でC++が使われています • 一部のコンテストサイトではこれとJAVAしか使えない • 色々便利 • いきなりC++を学び始めるのは難しいので、第0回講義では、 授業で扱った「十進ベーシック」で基本は解説します
- 7. 旭丘数理科学部 旭丘数理科学部 講義の前提 • 今回の講義では、簡単のため厳密さや正確さを欠いている 部分が多々あります • しかし、それらを追求してしまうと、非常に難解な説明か つ、長い時間が必要になります •よって、渋々簡単な説明に留めます。 • 中学校の理科みたいなものだと思っていただければ…
- 8.
- 9. 旭丘数理科学部 旭丘数理科学部 前提知識 • 学校の授業でやったような内容をスライド6枚くらいで復習 します。思い出せばいけます。 • 一応今後に向けてC++の記法もちょっとだけ取り入れます •紙1枚とペン1本あれば基本大丈夫です • プログラムは脳内再生してください
- 10. 旭丘数理科学部 旭丘数理科学部 前提知識 • 変数 • 数字や文字を入れられる •だいたいなんでも入れられる • 10進ベーシックでは LET で宣言 • 関数 • コンピュータに動作をさせるプログラム • print: 出力する sort: 並べ替える max:最大値を取るなど多種多様 • 自分で定義をすることも可能
- 11. 旭丘数理科学部 旭丘数理科学部 前提知識 • 演算子 • 数字と数字を一定のルールの上で計算するもの •以下のようなものがあります • 演算系 • + - : 足し算 引き算を行う 3 + 2 → 5 • * / : 掛け算 割り算を行う 3*2 → 6 • % : あまりの数を求める 10%3 → 1 (10進ベーシックにはない) • 比較系 true false を出力する • > < : 大小比較をする 3 > 5 → false • == : 等しいか比較する 4 == 8/2 → true
- 12. 旭丘数理科学部 旭丘数理科学部 前提知識 • if文 • プログラミング言語では以下のように書く •条件から、実行するプログラムを分岐させる事ができる • if文を重ねることもできる 10進ベーシック IF 判別したい条件 THEN true時実行したいプログラム ELSE false時実行したいプログラム END IF C++ if(判別したい条件){ true時実行したいプログラム } else{ false時実行したいプログラム }
- 13. 旭丘数理科学部 旭丘数理科学部 前提知識 • for文 • プログラミング言語では以下のように書く •TOの後ろの数値で ループの終了時の変数の値を指定する • iはカウンタ変数と呼ばれ、左の例だと、0 , 1 , 2 … 998 999 と順番に変 わりながらプログラムが実行される 10進ベーシック FOR i = 0 TO 999 STEP 1 実行したいプログラム NEXT I //この場合だと、iが0~999で1000回 //プログラムが実行される。 C++ for(int i = 0; i < 100; i++){ 実行したいプログラム } //この場合だと、iが0~99で100回 //プログラムが実行される。 //C++ では基本STEPは1固定 (本当は違う)
- 14. 旭丘数理科学部 旭丘数理科学部 前提知識 • 素数判定プログラムを作成！ • (10進ベーシックで作成) •必要なもの • INPUT関数 “INPUT 変数名” 変数にキーボードから入力 • PRINT関数 “PRINT 変数名” 変数の中身を出力をすることができる • SQRT関数 “SQRT(a)” aの平方根になる • MOD関数 “MOD(a,b)” aをbで割ったあまりになる • 制約 • 入力する値は、2 < 入力 < 1024 の整数とします
- 15. 旭丘数理科学部 旭丘数理科学部 素数判定プログラム PRINT “数値を入力してください” //文字を出力 INPUT N //Nに入力 LET flag = 0 FOR i = 2 TO a - 1 IF (a % i) = 0 THEN flag = 1 END IF NEXT i IF flag = 1 THEN PRINT “それは素数ではありません” ELSE PRINT”それは素数です” END IF
- 16. 旭丘数理科学部 旭丘数理科学部 解答例1 PRINT “数値を入力してください” //文字を出力 INPUT N //aに入力 LET flag = 0 FOR i = 2 TO N – 1 //ループ回数N回 IF MOD(N, i) = 0 THEN flag = 1 END IF NEXT i IF flag = 1 THEN PRINT “それは素数です” ELSE PRINT”それは素数ではありません” END IF
- 17. 旭丘数理科学部 旭丘数理科学部 正答例1の問題点 • 1回素数かどうかを求めるときに、入力サイズと同じだけ時 間がかかってしまう • 家庭用コンピュータでは、早い言語でも1秒間に10^9回く らいしかforのループを回すことができない •ゆえに1000000000007が素数かどうかなどを判別しようとする と時間が掛かる
- 18. 旭丘数理科学部 旭丘数理科学部 正答例 2 PRINT “数値を入力してください”// 文字を出力 INPUT N //Nに入力 LET flag = 0 FOR i = 2 TO SQRT(N) //ループ回数 𝑁回 IF MOD(N, i) = 0 THEN flag = 1 END IF NEXT i IF flag = 1 THEN PRINT “それは素数です” ELSE PRINT”それは素数ではありません” END IF
- 19. 旭丘数理科学部 旭丘数理科学部 なぜ行けるの？ • 約数を昇順に並べ、前からn番目と、後ろからn番目の約数 の積は元の数になることが知られているため、割り切れる か調べるのは 𝑁までで済む •Ex… 12の約数は 1 2 3 4 6 12 1*12 = 2*6 = 3*4 = 12となる
- 20. 旭丘数理科学部 旭丘数理科学部 前提知識の復習 • このように、数学的な工夫やプログラムの工夫によって、 プログラムの計算量を少なくしたり、プログラムをより簡 単に書けるようにすることが求められる • これがおもしろいと思う人は情オリ向いてます •面白いと思わない人も思考力を高めるために情オリに参加しま しょう
- 21.
- 22. 旭丘数理科学部 旭丘数理科学部 予備知識の学習 • 2個だけ新しいことを学びます • 配列 •計算量 • これらだけ知ってれば、発想次第で結構な問題が解けるよ うになります
- 23. 旭丘数理科学部 旭丘数理科学部 配列 • 配列 • 変数の列と考えることができる •下記例 サイズ10の配列 • 上の配列は DIM array (10) のように、 “DIM 配列名 (サイズ)” で宣言 • 配列の要素にアクセスしたい場合は、 配列名(場所)と書くことで 普通の変数として扱えます。 • 0からindexが始まることに注意 • 10進ベーシックで扱うときは先頭に”OPTION BASE 0” というおまじないが必要 0 1 2 3 4 5 6 7 8 9
- 24. 旭丘数理科学部 旭丘数理科学部 配列 • 例 OPTION BASE0 DIM array(10) FOR i = 0 TO 9 array(i) = 2*i NEXT i FOR j = 0 TO 9 PRINT array(j) NEXT j //出力 0 2 4 6 8 10 12 14 16 18 0 2 4 6 8 10 12 14 16 18 index 0 1 2 3 4 5 6 7 8 9
- 25. 旭丘数理科学部 旭丘数理科学部 計算量 • 計算量とは • そのプログラムが計算にどれだけ時間がかかるかの見積もり •アルゴリズムのAの計算量𝑇(𝑁)が概ね𝑃(𝑁)に比例することを 𝑇 𝑁 = 𝑂(𝑃 𝑁 )であると表し、アルゴリズムAの計算量を 𝑂(𝑃 𝑁 )であるという(Nは入力サイズ) (計算量とは何回プログラムを実行するかということ) • 難しいのでさっきの素数判定プログラムの話で具体例を考えます
- 26. 旭丘数理科学部 旭丘数理科学部 計算量 • 正答例1のアルゴリズム • 入力を受け取る1回 • iを1増やす N-2回 • if文を実行する N-2回 • 出力をする 1回 (実際にはこれらの時間は均一ではないが、ここでは簡単のため均一とする) • 先程の書き方で表すと、 • 𝑇 𝑁 = 2 𝑁 − 2 + 2 = 2N − 2 となり、これが概ね N に比例することが分かる -2の項が気になるかもしれませんが、 N = 100000の場合などを考えてみると、 ほぼこの2は影響しないことがわかります。 • 𝑃 𝑁 = 𝑁 • このアルゴリズムの計算量は𝑂 𝑁
- 27. 旭丘数理科学部 旭丘数理科学部 計算量 • 正答例2のアルゴリズム • 入力を受け取る1回 • iを1増やす 𝑁 − 2回 • if文を実行する 𝑁 − 2回 • 出力をする 1回 (実際にはこれらの時間は均一ではないが、ここでは簡単のため均一とする) • 先程の書き方で表すと、 • 𝑇 𝑁 = 2( 𝑛 − 2) + 2 = 2 𝑁 − 2 となり、これが概ね 𝑁 に比例することが分かる • 𝑃 𝑁 = 𝑁 • このアルゴリズムの計算量は𝑂 𝑁
- 28. 旭丘数理科学部 旭丘数理科学部 計算量 • 実際に、この2つのアルゴリズムの入力に対してかかる計算 量を考えると、このくらい時間が違う。 入力 N正答例1 正答例2 100000 100000 317 1000000 1000000 1000 10000000 10000000 3163 100000000 100000000 10000 1000000000 1000000000//以下実行不可 31623 10000000000 10000000000 100000 100000000000 100000000000 316228
- 29. 旭丘数理科学部 旭丘数理科学部 計算量 • 実際に計算量を求めようとする場合 • プログラムの計算回数を式に表して最高次係数以外とっぱらえば いいです。 •Ex 𝑇 𝑁 = 3𝑁3 + 𝑁 + 5 の場合、 𝑂 𝑁^3 • これでもわかりづらければ、 • 「プログラム中のループの回数」 • と考えてもらえばけっこうです。
- 30.
- 31. 旭丘数理科学部 旭丘数理科学部 • ここからは実際にプログラミングの面白さに触れていこう と思います • プログラムを組むことは流石に難しいので、紙に指針を書 いてみてください。 •初学者でも考えつけそうな問題を2つ用意しました。
- 32. 旭丘数理科学部 旭丘数理科学部 Ants • 長さLcmの竿の上をN匹のアリが毎秒1cmで動いています。 • アリが竿の端にたどりつくと竿から落ちます。 •竿は横幅が狭いのですれ違うことができず、二匹のアリが出会うと、お互いU ターンして反対の方向に進み始めます。 • 各アリについて、竿の左端からの現在の距離𝑋𝑖はわかりますが、向いている向 きはわかりません。 • すべてのアリが落ちるまでにかかる最小の時間と最大の時間を求めてください。 • 制約 • 1 ≤ 𝐿 ≤ 106 • 1 ≤ 𝑁 ≤ 106 • 0 ≤ 𝑥𝑖 ≤ 𝐿 • 計算回数の上限は10^9とします x1 x2 x3 …
- 33. 旭丘数理科学部 旭丘数理科学部 Ants • ナイーブな指針 • アリがそれぞれ右を向いているか左を向いているかでシミュレー ションして、最大値と最小値を求める。 •1匹につき2通りの場合があるので、ループの回数は2𝑁 通り。 • 1回のシミュレーションは𝑂(𝑁)で行うことができるので、 • 合計で計算量は𝑂(2𝑁 )となる • (2𝑁は 𝑁よりも増加速度が大きい関数のため) • 最大のケースを考えると、2^(10^6)は明らかに10^9より大きいの で、絶対に間に合わない。
- 34. 旭丘数理科学部 旭丘数理科学部 Ants • 正答例 • 2匹のアリがUターンすることに注目をする。 •実際は、アリがUターンし合うということは、アリがすれ違うこととこ の場合は等しい。 • これによってすべてのアリは独立して動けるようになる。 • よって最大最小を求めるためには1体1体のアリの端までの距離を 調べれる事によって求めることができる。 • 計算量は𝑂(𝑁)より、最大ケースでも10^6で済む。 • 発想によって大幅に計算量を削減できる
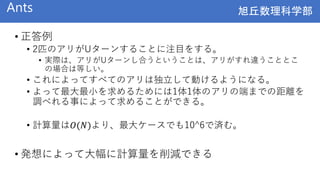
- 35. 旭丘数理科学部 旭丘数理科学部 Ants OPTION BASE 0 LETL, N DIM X(N) FOR i = 0 TO N INPUT X(N) NEXT N LET mintT = 0 , maxT = 0 FOR i = 0 TO N LET minT = max(minT , min(x[i] , L - x[i]) // max(a,b)でa,bの大きい方 min(a,b)でa,bの小さい方 LET maxT = max(maxT , max(x[i], L – x[i]) NEXT I PRINT minT PRINT maxT END
- 36. 旭丘数理科学部 旭丘数理科学部 休憩 • 年齢当てゲーム • 目の前に0~127歳の人間がいます。 •その人にYes/Noで答えられる質問をして、年齢を確定させたい です。 • 最低でも質問は何回必要でしょうか？ • (128回ではないです)
- 37. 旭丘数理科学部 旭丘数理科学部 年齢当てゲーム • 答え • ７回で確定させることが可能。 •方法 • 64歳以上ですか？ • Yesの場合 96歳以上ですか？ • NOの場合 32歳以上ですか？ この受け答えを7回やれば、その人の歳が確定する。 • この場合、プログラムでこれを実行すると、 • 𝑂(log2 𝑁)となる(底の2は省略されることが多い) • 一応logの説明(log𝑎 𝑏 = 𝑥 は 𝑎𝑥 = 𝑏 と同値)
- 38. 旭丘数理科学部 旭丘数理科学部 ペア和最小化問題 • N個の整数 𝑎0,𝑎1, … 𝑎𝑛−1と𝑏0, 𝑏1, … 𝑏𝑛−1がそれぞれ昇順に並 んでいる • 2つの整数列からそれぞれ1こずつ整数を選び、和をとる • その和として考えられるうち、整数K以上の範囲の最小値を 求めてください • ただし、条件を満たすペアが1つ以上存在するものとします • 制約 • 1 ≤ 𝑎𝑖, 𝑏𝑖 ≤ 105 • 𝑎𝑖 ≤ 𝑎𝑖+1, 𝑏𝑖 ≤ 𝑏𝑖+1 • 1 ≤ 𝑁 ≤ 105 1 < 𝐾 < 105 • 計算回数の上限は10^9
- 39. 旭丘数理科学部 旭丘数理科学部 ペア和最小化問題 • ナイーブな解法 • 𝑎𝑖,𝑏𝑗(1 ≤ 𝑖, 𝑗 ≤ 𝑁)をすべてのパターン試し、K以上の最小値を求 める。 • 計算量は、forのループを2重に重ねることとなるので、𝑂(𝑁2) • 最大ケースの𝑁 = 105だと、𝑁2 = 1010となってしまい、実行時間 をオーバーしてしまう。 • どうすればいいのか → 年齢当てゲームの発想を用いる！
- 40.
- 41. 旭丘数理科学部 旭丘数理科学部 ペア和最小化問題 • Hint • 計算量は、O(NLogN) となる。 • aを1つに決めたときにbを選ぶには…?
- 42. 旭丘数理科学部 旭丘数理科学部 ペア和最小化問題 • Hint • 計算量は、O(NLogN) となる。 • aを1つに決めたときにbを選ぶには…? • 𝐾 − 𝑎𝑖 に注目すると…?
- 43.
- 44.
- 45.
- 46.