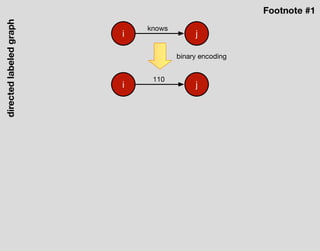
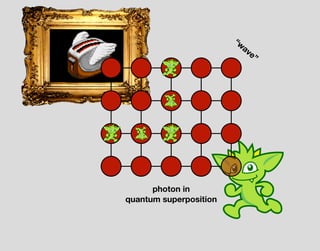
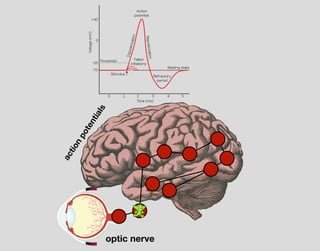
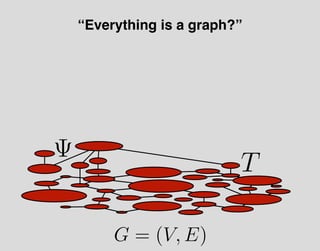
The document discusses the idea of the universal graph - that everything can be modeled as a graph of vertices and edges. It proposes some open problems regarding how to model processes and qualia as part of the universal graph structure, and how one might manipulate the laws of physics by altering the processes that govern the evolution of the physical world graph.

1. Dr. Marko A. Rodriguez
Director of Engineering at DataStax, Inc.
Project Management Committee, Apache TinkerPop

2. The universal graph is a theoretical construct capturing the idea that every aspect
of reality can be modeled as a graph composed of vertices and edges and, as
such, reality is a graph. From the physical world of atoms, people, and galaxies
to the mental planes of thoughts, words, and knowledge, there exists a universal
graph hosting all such structures. While this idea is enticing, there are still strides
to be made in coming to terms with a reality that is not composed of atoms bound
by spacetime, but instead, a graph composed of vertices united by edges.
Abstract
https://doi.org/10.5281/zenodo.583293
Open Problems in the Universal Graph Theory
Rodriguez, M.A., "Open Problems in the Universal Graph Theory," GraphDay `17, 2(2), pages 1-5, San Francisco, CA, June 2017.

3. Introduction

4. “Everything is a graph.”

6. Power Grids
https://en.wikipedia.org/wiki/Electrical_grid

7. Power Grids
https://en.wikipedia.org/wiki/Electrical_grid

9. Vascular System
https://en.wikipedia.org/wiki/Circulatory_system

10. Vascular System
https://en.wikipedia.org/wiki/Circulatory_system

12. Protein Chains
https://en.wikipedia.org/wiki/Protein_complex

13. Protein Chains
https://en.wikipedia.org/wiki/Protein_complex

15. Galactic Filament
https://en.wikipedia.org/wiki/Galaxy_filament

16. Galactic Filament
https://en.wikipedia.org/wiki/Galaxy_filament

17. “Everything is a graph.”

18. “Everything is a graph.”
Universe Vertices + Edges=

19. “Everything is a graph.”
Universe Vertices + Edges=
G = (V, E)

22. Graph Traversal
Graph Computing
Structure Process

23. Structure
Graph
Process
Traversal
Graph Computing
G = (V, E)
?
“Everything is a graph.”

24. Time:
The Process of Change

25. (V, E) = G ←− µ t ∈ T ψ −→ Ψ = (F, S)
Gremlin Graph Traversal Machine
Rodriguez, M.A., “The Gremlin Graph Traversal Machine and Language,” Proceedings of the 15th Symposium on Database
Programming Languages (DBPL 2015), pages 1–10, ISBN:978-1-4503-3902-5, doi:10.1145/2815072.2815073, ACM, October 2015.
http://arxiv.org/abs/1508.03843

26. (V, E) = G ←− µ t ∈ T ψ −→ Ψ = (F, S)
Gremlin Graph Traversal Machine
Graph Traversers Traversal

27. (V, E) = G ←− µ t ∈ T ψ −→ Ψ = (F, S)
Gremlin Graph Traversal Machine
Graph Traversers Traversal
Data Processing Units Program

28. (V, E) = G ←− µ t ∈ T ψ −→ Ψ = (F, S)
Gremlin Graph Traversal Machine
Graph Traversers Traversal
Data Processing Units Program
Structure ProcessProcessor

29. G = (V, E)

30. g.V(1).out(‘knows’).out(‘created’)
G = (V, E)

31. G = (V, E)
g.V(1).out(‘knows’).out(‘created’)

32. G = (V, E)
g.V(1).out(‘knows’).out(‘created’)

33. G = (V, E)
g.V(1).out(‘knows’).out(‘created’)

34. G = (V, E)
g.V(1).out(‘knows’).out(‘created’)

35. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)

36. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)

37. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)

38. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)

39. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)
G ←− µ t ∈ T ψ −→ Ψ

40. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)
µ
ψ
t ∈ T
G ←− µ t ∈ T ψ −→ Ψ

41. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)
µ
ψ
µ
ψ
T

42. op=V
args=1
op=out
args=knows
op=out
args=created
nextnext
Ψ = (F, S)
G = (V, E)
µ
ψ
µ
ψ
µ
ψ
T

43. Ψ = (F, S)
G = (V, E)
T

44. Ψ = (F, S)
G = (V, E)
T

45. Ψ = (F, S)
G = (V, E)
T

46. Ψ = (F, S)
G = (V, E)
T

47. G = (V, E)
“Everything is a graph?”
Ψ
T

48. G = (V, E)
“Everything is a graph?”
Ψ
T
No — All that exists is a static structure.

49. G = (V, E)
“Everything is a graph?”
Ψ
T
Fine — Create a traversal that executes
the graph encoded traversal. Ψ′

50. g.withSack(0).withSideEffect('drain',[1]).withSideEffect('fill',[]).
V().has('source','g').as('parent').
repeat(out('next').as('step').
map(values('arg').fold()).as('args').
sideEffect(select('drain').unfold().
choose(select(last,'args').count(local).is(0),
choose(select(last,'step').by('op')).
option('V',V().hasLabel(not(within('step','traversal')))).
option('out',out()).
option('in',in()).
option('both',both()).
option('outE',outE()).
option('inE',inE()).
option('bothE',bothE()).
option('inV',inV()).
option('outV',outV()).
option('otherV',otherV()).
option('values',values()).
option('barrier',barrier()).
option('dedup',dedup()).
option(none,identity()).
choose(select(last,'step').by('op')).
option('V', V().hasLabel(not(within('step','traversal'))).
where(within('args')).by(id).by()).
option('has',filter(union(label(),properties().
where(within('args')).by(key).by().value()).
filter(predicate("it.path(last,'args')[1].test(it.get())")))).
option('out',outE().where(within('args')).by(label).by().inV()).
option('in',inE().where(within('args')).by(label).by().outV()).
option('both',bothE().where(within('args')).by(label).by().otherV()).
option('outE',outE().where(within('args')).by(label).by()).
option('inE',inE().where(within('args')).by(label).by()).
option('bothE',bothE().where(within('args')).by(label).by()).
option('values',properties().where(within('args')).by(key).by().value()).
option('barrier',barrier()).
option(none,identity())).
store('fill')).
…
Ψ′
Footnote #2

51. sideEffect(consumer("it.sideEffects('drain').clear()")).
sideEffect(select('fill').unfold().store('drain')).
sideEffect(consumer("it.sideEffects('fill').clear()")).
select(last,'step').
choose(has('op','repeat').and().out('next').has('op','times'),
select(last,'step').as('parent').
sack(assign).by(out('next').values('arg')).out('child').as('step'),
choose(select(last,'parent').has('op','repeat').and().out('next').count().is(0),
choose(sack().is(gt(1)),
sack(minus).by(constant(1)).select(last,'parent').out('child').as('step'),
select(last,'parent').as('step').out('parent').as('parent').select(last,'step')),
identity()))).
until(out('next').count().is(0)).
select('drain').
choose(select(last,'step').has('op',within('fold','sum','mean','min','max','count','groupCount')),
choose(select(last,'step').by('op')).
option('fold',identity()).
option('sum',map(unfold().sum())).
option('mean',map(unfold().mean())).
option('min',map(unfold().min())).
option('max',map(unfold().max())).
option('count',map(unfold().count())).
option('groupCount',map(unfold().groupCount())),
unfold())
…
https://www.datastax.com/dev/blog/a-gremlin-implementation-of-the-gremlin-traversal-machine
Rodriguez, M.A., “A Gremlin Implementation of the Gremlin Traversal Machine,” DataStax Engineering Blog, October 2016.
Footnote #2

52. Ψ′
⊂ G
Footnote #2

53. G = (V, E)
Ψ
T
Ψ′

54. G = (V, E)
µ
ψ
Ψ
T
Ψ′
T′

55. G = (V, E)
“Everything is a graph?”
µ
ψ
Ψ
T
Ψ′
T′

56. G = (V, E)
“Everything is a graph?”
µ
ψ
Ψ
T
Ψ′
T′ No — Now there must exist a
traversal to execute the
traversal that is executing the
traversal.
Ψ′
Ψ
Ψ′′

57. Ψ, Ψ′
, Ψ′′
, Ψ′′′
, . . . , Ψ∞
⊂ G

58. Ψ, Ψ′
, Ψ′′
, Ψ′′′
, . . . , Ψ∞
⊂ G
program program programprogram program
processor processor processor processorprocessor

59. Ψ, Ψ′
, Ψ′′
, Ψ′′′
, . . . , Ψ∞
⊂ G
Bytecode, Virtual Machine, Physical Machine, Physics, …
program program program program
processor processor processor processor
program program programprogram program
processor processor processor processorprocessor

60. G ←− T −→ Ψ
Folding Process into Structure
G = (V, E)
“Everything is a graph.”

61. Open Problem #1
How can the universal graph
evolve without requiring processes
to exist “outside” itself?

62. i j
knows
directedlabeledgraph Footnote #1
Rodriguez, M.A., “Mapping Semantic Networks to Undirected Networks,” International Journal of Applied Mathematics and
Computer Sciences, 5(1), pages 39-42, ISSN:2070-3902, World Academy of Science Engineering and Technology, 2009.
http://arxiv.org/abs/0804.0277

63. i j
knows
i j
110
binary encoding
directedlabeledgraph Footnote #1

64. i j
knows
i j
110
b1 b2 b3
binary encoding
directedlabeledgraph Footnote #1

65. i j
knows
i j
110
b1 b2 b3i j
b1 b2 b3
binary encoding
label encoding
directedlabeledgraphdirectedgraph Footnote #1

66. b1 b2 b3i j
directedgraph Footnote #1

67. b1 b2 b3i j
directedgraph Footnote #1
b1 b2e1
e2
e3

68. b1 b2 b3i j
directedgraphundirectedgraph Footnote #1
b1 b2e1
e2
e3
b1 b2e1
e2
e3
b3 j
i
“dots and lines”
direction encoding

69. undirectedgraph Footnote #1
j
i
“dots and lines”
i j
knows
directedlabeledgraph
bijection

70. Thought:
The Structure of Experience

72. physical object
physical object

73. physical spacetime

74. Rodriguez, M.A., Watkins, J.H., “Quantum Walks with Gremlin,” Proceedings of GraphDay ’16, pages 1-16, Austin, TX, January 2016.
http://arxiv.org/abs/1511.06278
physical photon
“particle”

75. photon in
quantum superposition
“w
ave”

76. photon in
quantum superposition
“w
ave”

77. photon in
quantum superposition
“w
ave”

78. physical photon
“particle”
To be continued…

79. physical brain

80. photons

81. retina
light rods and
cones

82. optic nerve
actionpotentials

83. thalamus
“spreading activation”

84. lateral geniculate nucleus
“neurotransmitter mediated energy diffusion”

85. lateral geniculate nucleus
velocity of movement

86. visual cortex — V1
occipital lobe
edge detection

87. visual cortex — V2 through V4
occipital lobe
com
plex
shapes

88. visual cortex — V5 through V6
occipital lobe
m
otion
and
holistic
objects

89. inferior temporal gyrus
temporal lobe
“flying” “toaster”
“grandmother cells”

90. “Everything is a graph.”

91. Qualia Graph
Material Graph
“PhysicalWorld”“ConsciousWorld”
M ⊂ G
Q ⊂ G
Q ∩ M ∼ ∅

92. Open Problem #2
How does the universal graph
encode the qualia of thought as
vertices and edges?

93. Footnote #4
=
The process is the conscious experience…

94. Footnote #4
…but process has a structural, graph encoding.
G←−T−→Ψ
“Everythingisagraph.”
G=(V,E)

95. Creativity:
Altering the Structure of Process

96. G ←− T −→ Ψ
Graph Traversers
Traversal

97. Laws of Physics
G ←− T −→ Ψ
Physical World
Graph Traversers
Traversal
Structure
Process

98. Laws of Physics
G ←− T −→ Ψ
Physical World
Matter-energy
Spacetime
Quantum
Gravity
Graph Traversers
Traversal
Data
Structure
Algorithm

99. Laws of Physics
G ←− T −→ Ψ
Physical World
Matter-energy
Spacetime
Quantum
Gravity
“Everything is a graph.”
G = (V, E)
Graph Traversers
Traversal

100. Matter-energy
Spacetime
Quantum
Gravity
µ ψ
t
G ←− T −→ Ψ
G = (V, E)

101. Matter-energy
Spacetime
Quantum
Gravity
µ ψ
t
G ←− T −→ Ψ

102. Matter-energy
Spacetime
Quantum
Gravity
µ ψ
t
G ←− T −→ Ψ
Laws of Physics
Manipulation
Technology
Ψ′

103. Ψ′
←− T′
Matter-energy
Spacetime
Quantum
Gravity
µ ψ
t
G ←− T −→ Ψ
ψ
Laws of Physics
Manipulation
Technology
t′

104. Matter-energy
Spacetime
Quantum
Gravity
µ ψ
t
G ←− T −→ Ψ
µψ
Ψ′
←− T′
−→ G′
Laws of Physics
Manipulation
Technology
Designer Gravity
“Everything is a graph.”
t′

105. Open Problem #3
If process is as malleable as structure, then
how does one get a reference to the “laws of
physics” in order to alter the evolution of the
physical world?

106. Thank you.
Coming in 2020
“A Graph Computing Book”
2018-2019
Sabbatical