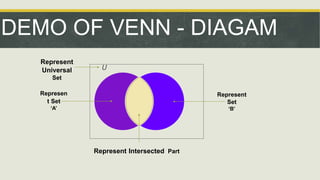
This document provides an overview of sets and set theory concepts including: - German mathematician George Cantor developed the ideas of set as a mathematical theory in the 19th century and John Venn developed Venn diagrams to represent sets. - Common set operations are defined including union, intersection, difference, complement, and examples are provided to demonstrate each operation. - A Venn diagram uses overlapping circles to visually represent sets and the relationships between elements in different sets.

1. Name : Raunak Shah

2.  German mathematician George Cantor (1844-1918) developed the ideas
of set as mathematical theory in nineteenth century. John Euler Venn
developed the method of representing the sets by closed figures called
Venn diagrams.
 Now, we use Venn diagram so represent set, set relations and set
operations in a simplified form.
History of Set

3. Content
1. Union
2. Intersection
3. Difference
4. Complement
5. Subsets
6. Cardinality of set
7. Universal set
8. Venn diagram

4. What is set ?
A set is a collection of distinct object or
numbers , represented within the curly
brackets { }. For example: {1,2,3,4} is a
set of numbers.
The objects in a set are called the
elements or members of the set.

5. What is Union (∪) ?
 Basically, Union means uniting or gathering all the elements from all the
sets and making a single set is known as union.
 For example , A has set containing of elements {1,2,3} and B has set of
elements {4,5,6} Now if the operation is A ∪ B then we should us the
union method and unite all the elements and make a single set like A ∪ B
= {1,2,3,4,5,6}.

6. Intersection(∩)
Intersection means the set which contains the elements that are common to the both the
sets is known as Intersection and it can be written as in set builder notation.
Example A∩B = {x : x is a member of A and x is a member of B}.
Example : Find the intersection of two sets.
A = { 1 , 3 , 5 , 6 , 8 }
B = { 2 , 3 , 6 , 7 , 8 }
Now , We know that both the set have common elements know we need to use A∩B to find
the answer and only the common elements should be written in A∩B set.
So ,
A = { 1 , 3 , 5 , 6 , 8 }
B = { 2 , 3 , 6 , 7 , 8 }
A∩B = { 3 , 6 , 8 }

7. DIFFERENCE (-)
What is the difference in a set?
The set operation difference between sets implies subtracting the elements from
a set which is similar to the concept of the difference between numbers. The
difference between sets A and set B denoted as A − B lists all the elements that
are in set A but not in set B
For example if A={1,2,3} and B={3,5}, then A−B={1,2}.

8. COMPLEMENT (Ā)
The Complement of set is defined as the set which contains the elements
present in universal set but not in other set is known as complement.
For example, Set U = {2, 4, 6, 8, 10, 12 } and set A = {4,6,8},
then the complement of set A is Ā = {2,10,12}.

9. UNIVERSAL SET
The universal set is the set that has all the elements that are being
considered in the problem
It is Often shown using the symbol ‘U’.
In a Venn Diagram, the Universal Set is indicated by a rectangle around
the sets.

10. What is Cardinality
The cardinality of a set is the total number of
elements in the set.
Note : To denote the cardinality of a set we use :
n(A)
Example :
A = { 2, 4, 6, 8, 10, 12 }
Ans = n(A) = 6
B = { All the odd number form 1 to 20 }
Ans = |B| = 10
C = { 1, 2, 3, 4, 16, 17, 18, 19, 20 }
Ans = n(c) = 9

11. WHAT IS VENN – DIAGRAM ?
A Venn – Diagram is a diagram in which mathematical sets are represented by
overlapping circles within a boundary representing the universal set, so that all the
possible combinations of the relevant properties are represented by distinct areas of
the diagram.

12. DEMO OF VENN - DIAGAM
Represen
t Set
‘A’
Represent Intersected Part
Represent
Set
‘B’
Represent
Universal
Set
U

13. Subsets , Proper Subsets and Empty Set
Subsets
A set A is a subset of another set B if all
elements of the set A are elements of
the set B. In other words, the set A is
contained inside the set B. The
subset relationship is denoted as
A⊂B
Example: If set A has {X, Y} and set
B has {X, Y, Z}, then A is the subset
of B because elements of A are also
present in set B.
Proper Subset
A proper subset of a set A is a
subset of A that is not equal to A.
In other words, if B is a proper
subset of A, then all elements of B
are in A but A contains at least
one element that is not in B. For
example, if A={1,3,5} then B={1,5}
is a proper subset of A.
Empty Set
A set which does not
contain any element is
called the empty set or
the null set or the void
set.