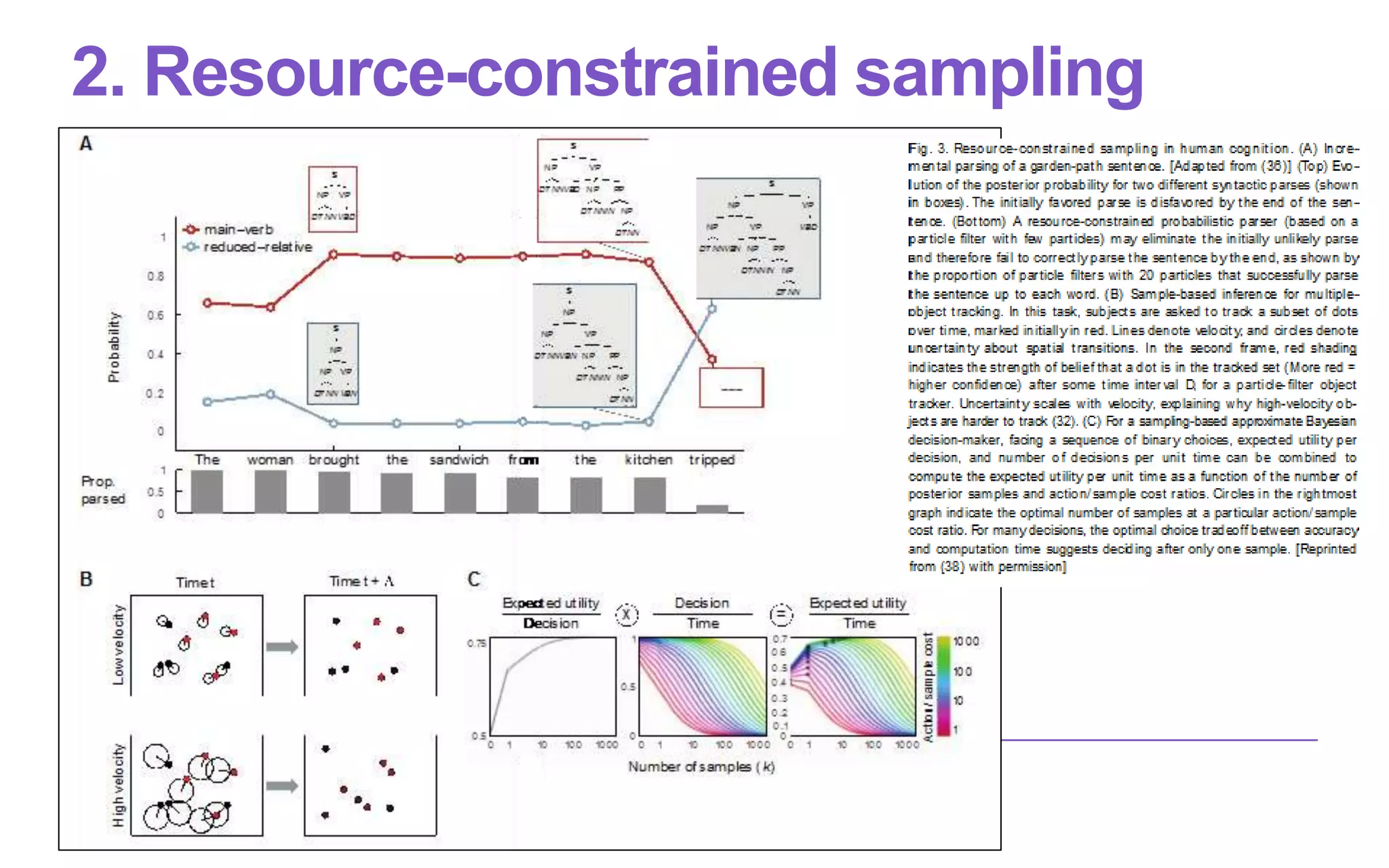
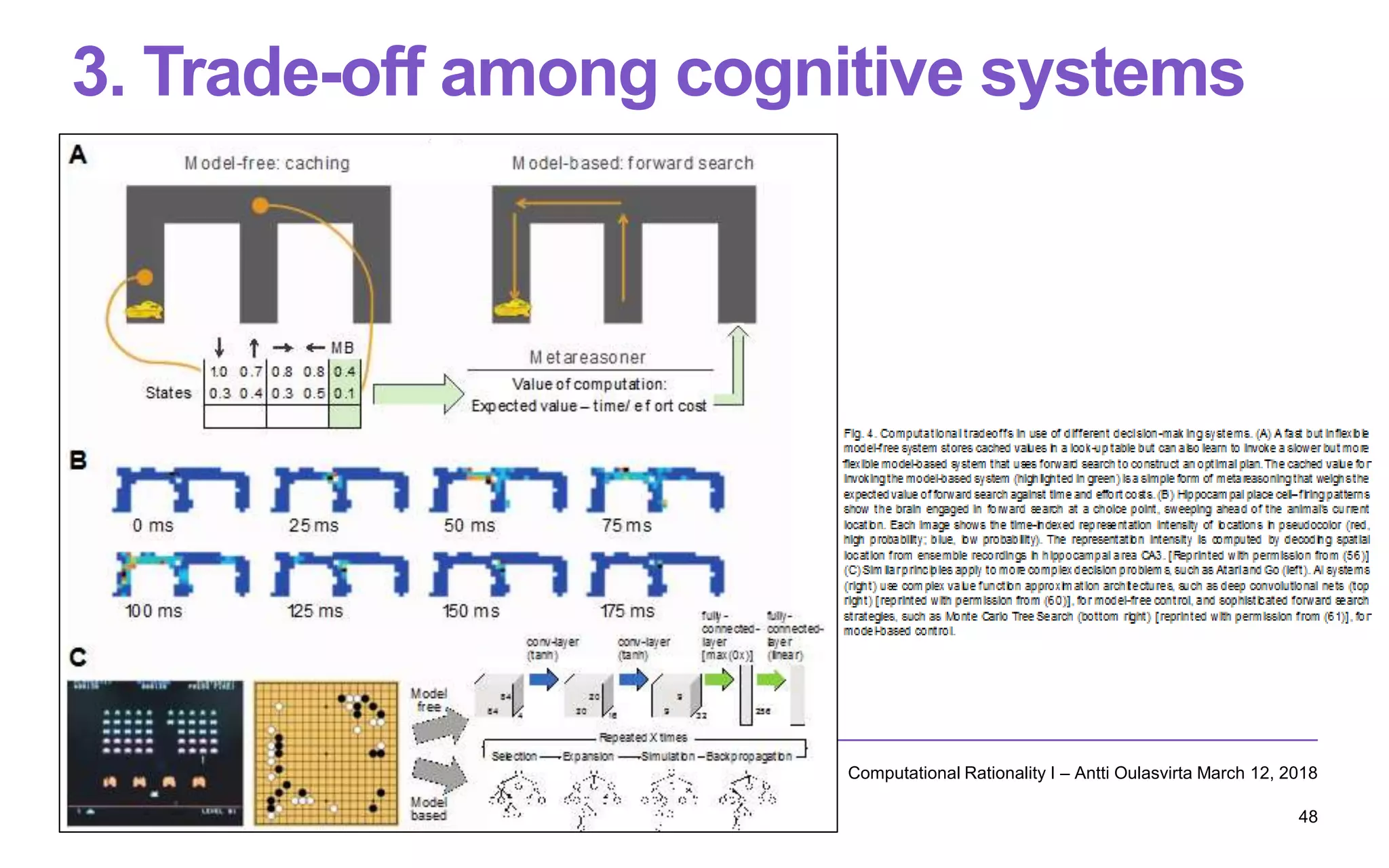
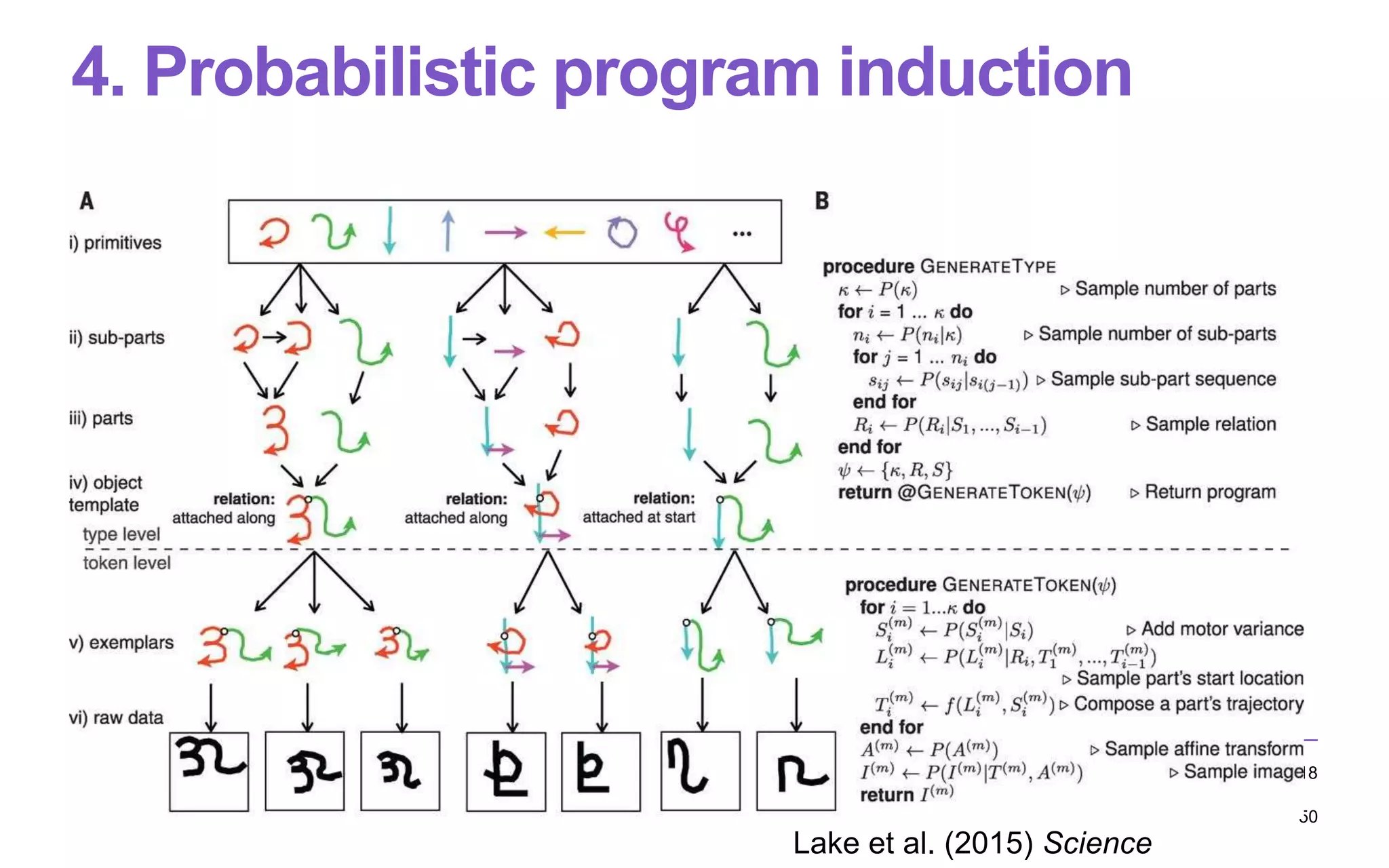
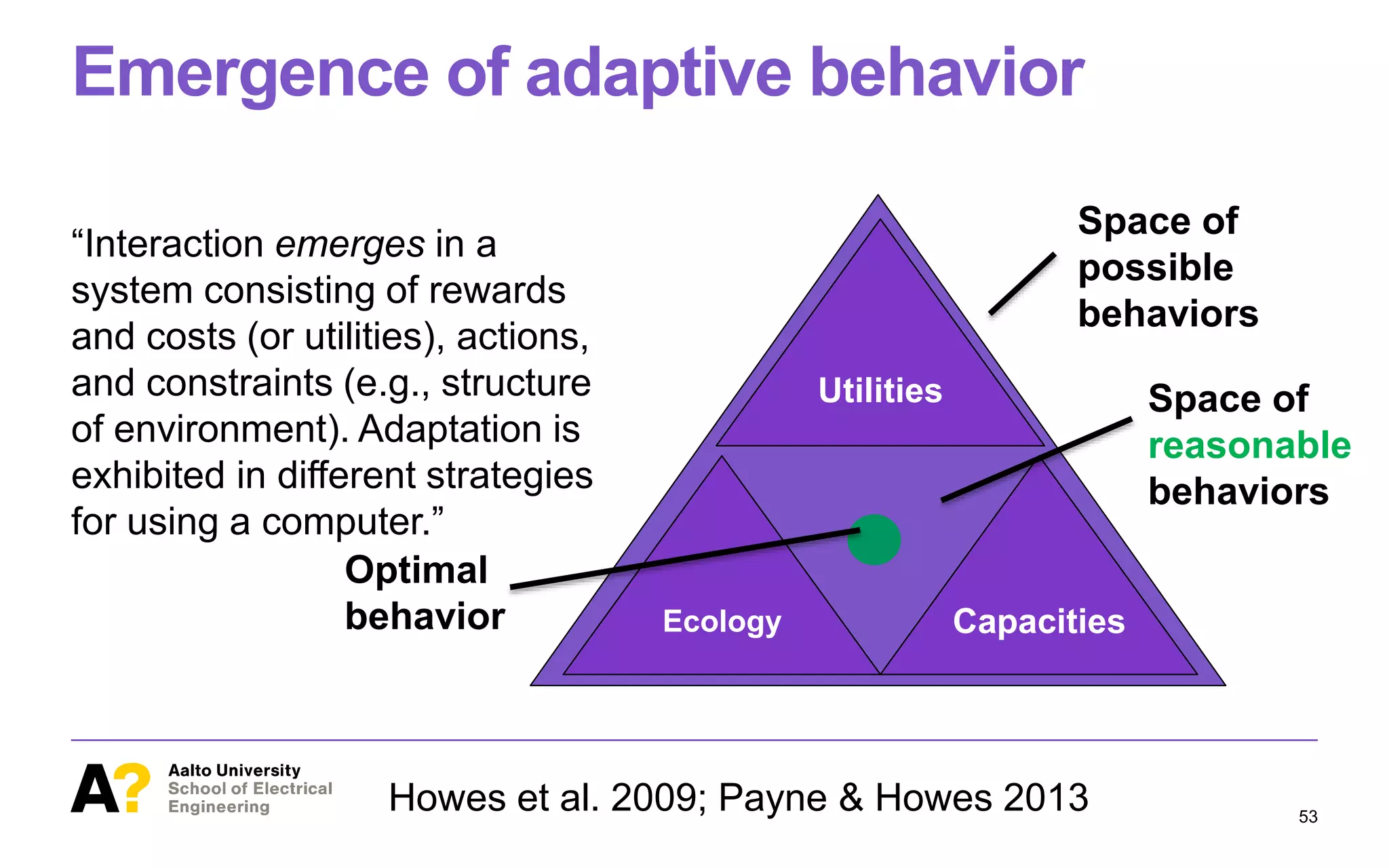
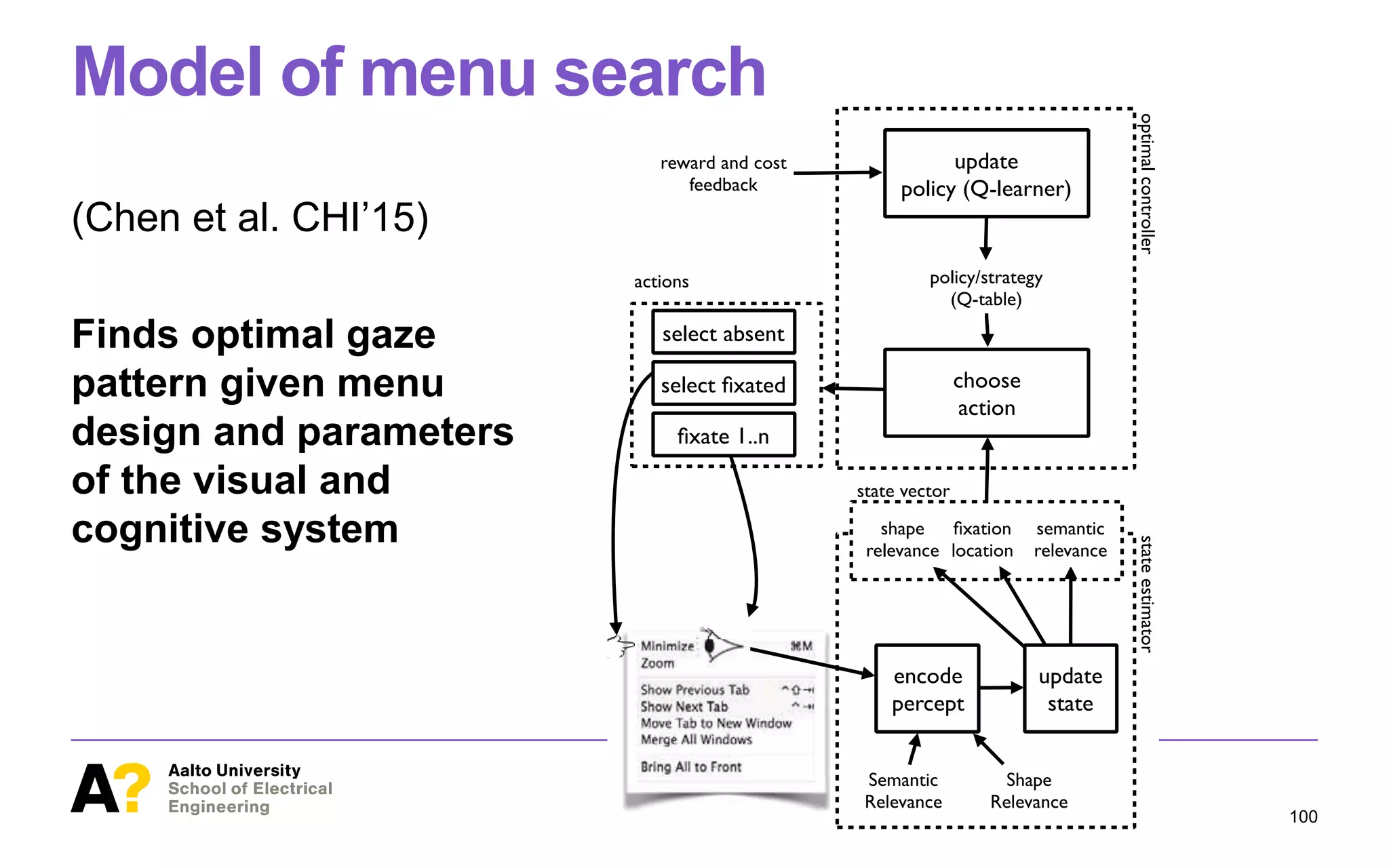
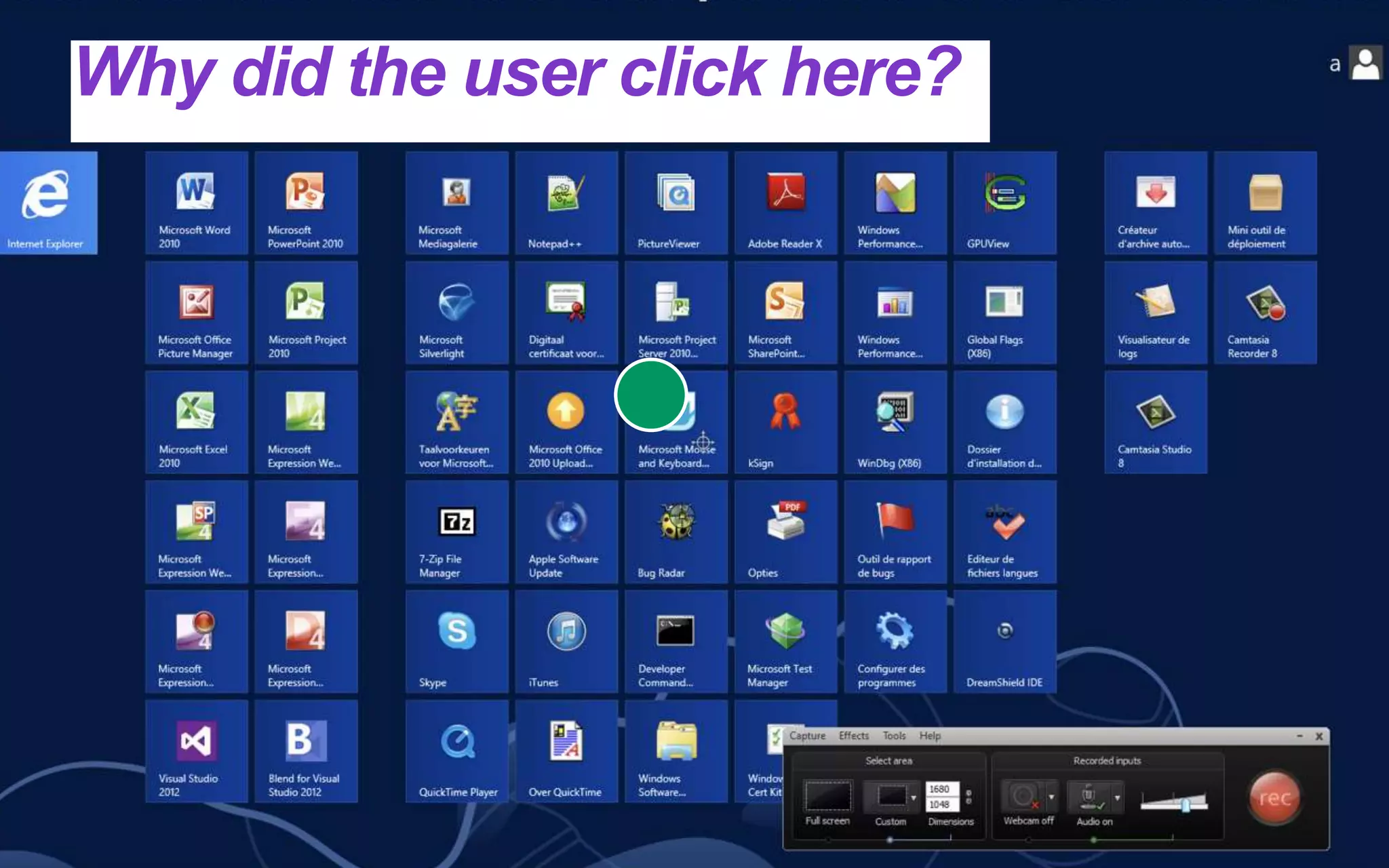
The lecture on computational rationality by Antti Oulasvirta explores cognitive principles that govern human-computer interactions, emphasizing the adaptive behaviors influenced by the environment and the decision-making processes involved. It discusses strategies for modeling human cognition as rational agents under constraints, including the challenges of generalization, planning, and exploration. Applications of these principles span across machine learning, cognitive science, and neuroscience, aiming to enhance our understanding of decision-making and behavior in real-world settings.





















![Example: Time-to-contact estimation
Time-to-collision can be estimated with a simple
formula from retinal input
26
Rushton & Wann 1999 Nature
cal evidence2 for theearly combination of sizeand disparity
motion signals(dq/dt + da/dt), and neurophysiological evidence
for thecombination of opticsizeand disparity(q + a) at an early
stageof visual processing15. A TTC estimatecan bebased on a
ratio of thesecombined inputs:
TTCdipole = (q + a) / (dq/dt + da/dt) (4)
Weadopt thelabel ‘dipole’ from theoryon textureperception16 .A
singlepoint viewedbytwoeyesspecifiesabinocular dipole,andtwo
points(such astwooppositeedgesof an object) viewedbyoneeye
specifyamonocular dipole. Our model sumsdipolesand doesnot
distinguish their origin.Analternativemeansof estimatingtheratio
in Equation 4isto takethechangein thesummed dipolelength
withinalogarithmiccoordinatesystem:TTCdipole= d[ln (q + a)]/dt.
Theretinoto
approaches(
theearlier ar
formableobje
tion 4isequi
TTCdipole = (
Hencewhen
distance(I =
weightingof
betoward an
toward TTCd
matereliesu
changeisbe
respon
thresho
biasesTemporal error with looming TTC plateau is 750 ms](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-26-2048.jpg)



























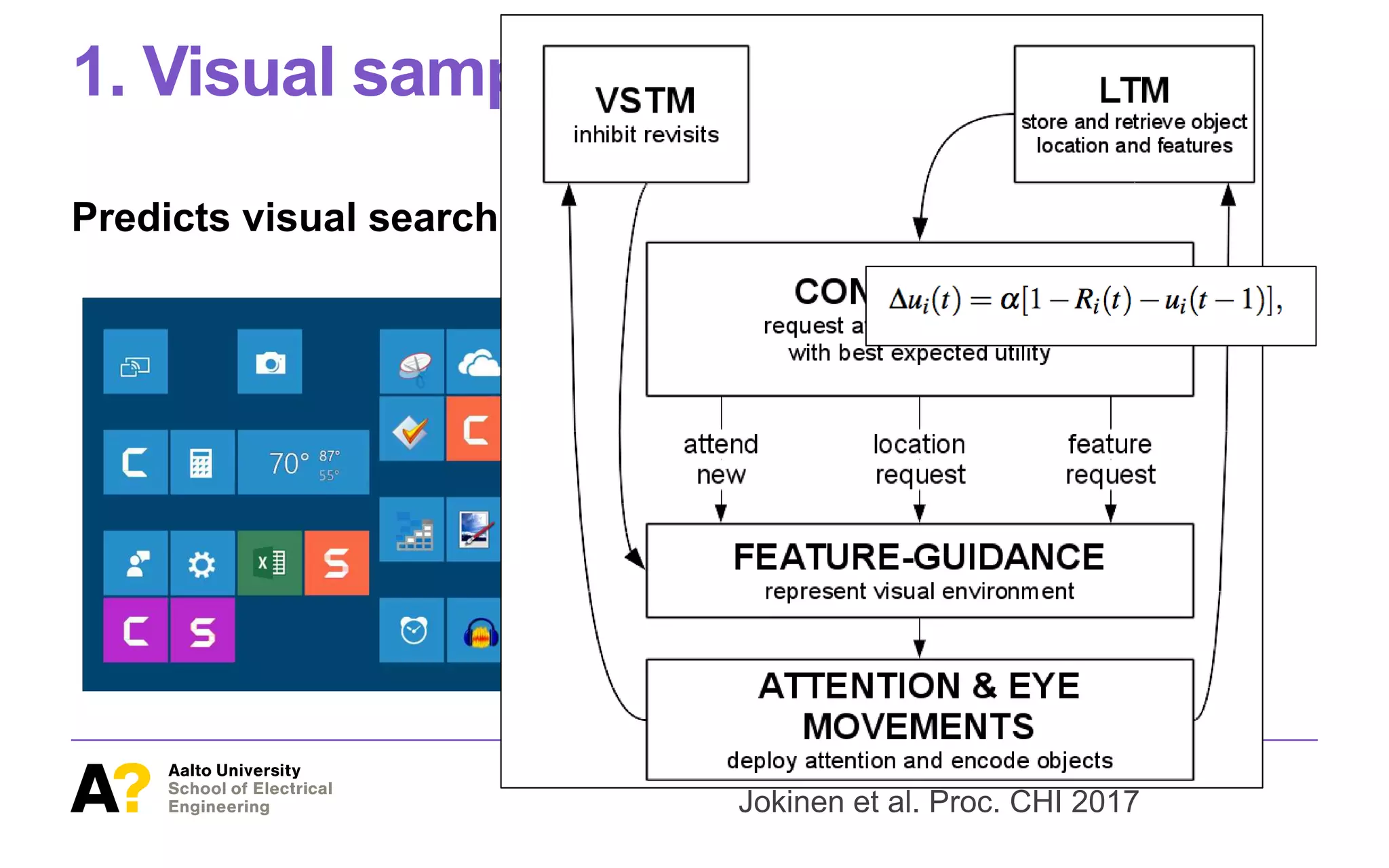
![1. Visual sampling
Utility learning
Jokinen et al. Proc. CHI 2017
Figure 2. On the basis of expected utility, the controller requests atten-
Encoding an object allows the model to decide whether it is
the target or a distractor. Before themodel can encode any ob-
jects, it needs to attend one. Thefeature-guidance component
holds a visual representation of the environment, and at the
controller’srequest it resolvestherequest to deploy attention
to oneof theobjectsin it. Theattended target isdetermined by
the properties of thevisual objects. Their properties’ presence
in the visual representation is based on their eccentricity. A
feature isvisually represented if its angular size islarger than
ae2
− be, (1)
where eistheeccentricity of theobject (in thesame units as
the size) and a and b are free parameters that depend on the
visual featurein question. Their values, from theliterature, are
a = 0.104 and b = 0.85 for colour, 0.14 and 0.96 for shape,
and 0.142 and 0.96 for size [35].
On thebasis of therepresented visual features, each object is
given a total activation as a weighted sum of bottom-up and
top-down activations. Bottom-up activation isthesaliency of
an object, calculated asthe dissimilarity of its features v to all
other objects of theenvironment, weighted by thesquare root
of the linear distance d between the objects:
objects features](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-63-2048.jpg)






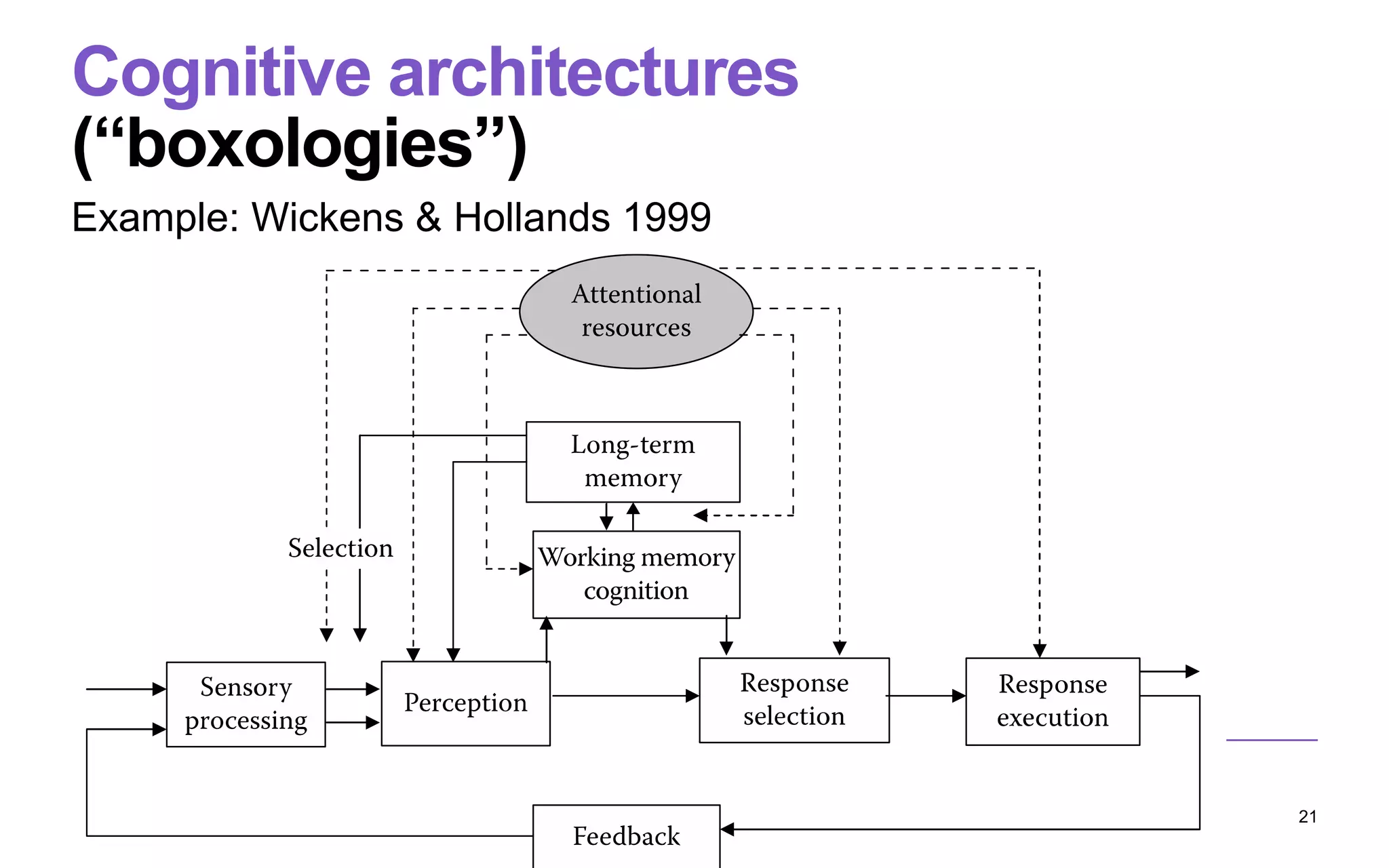
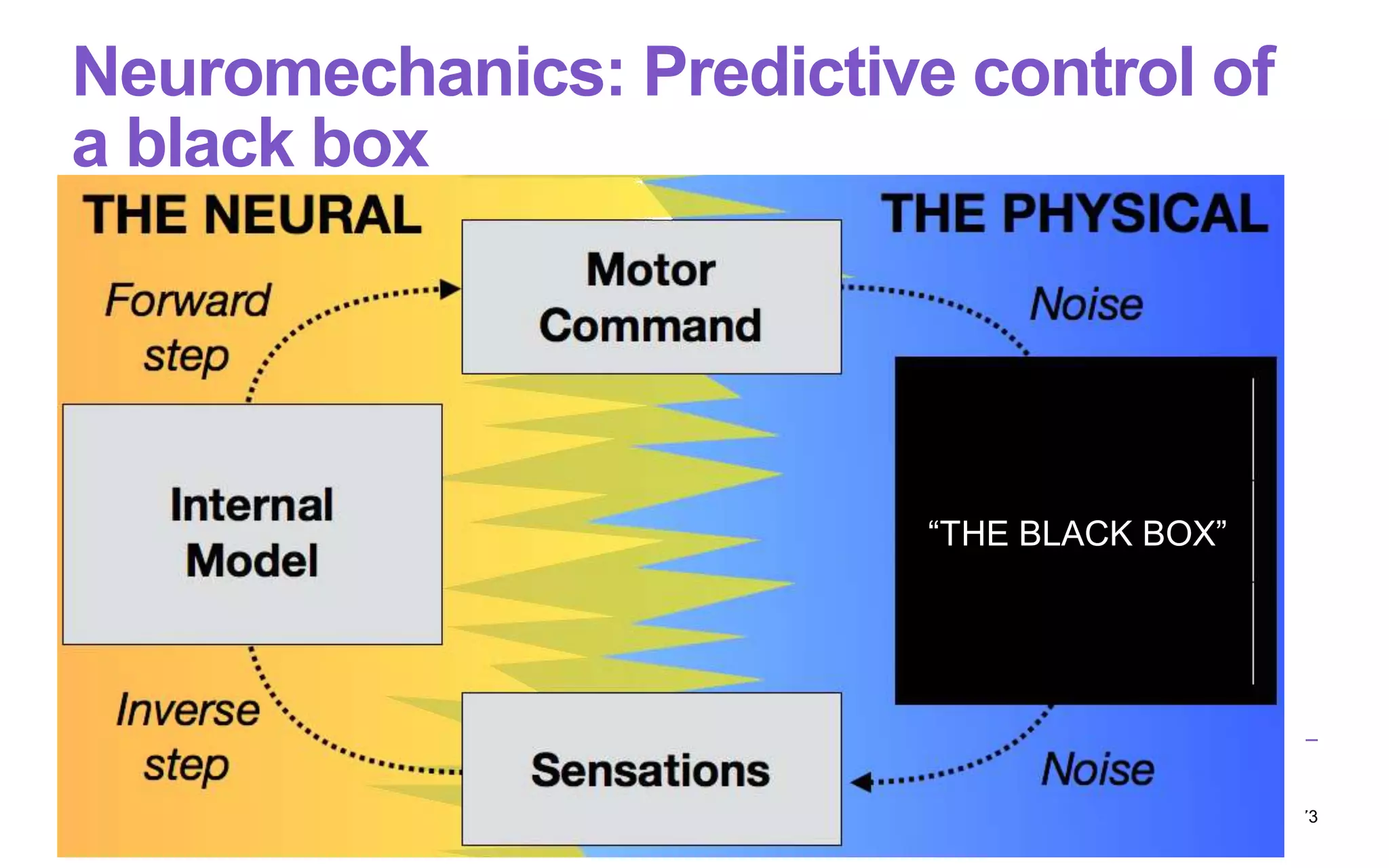
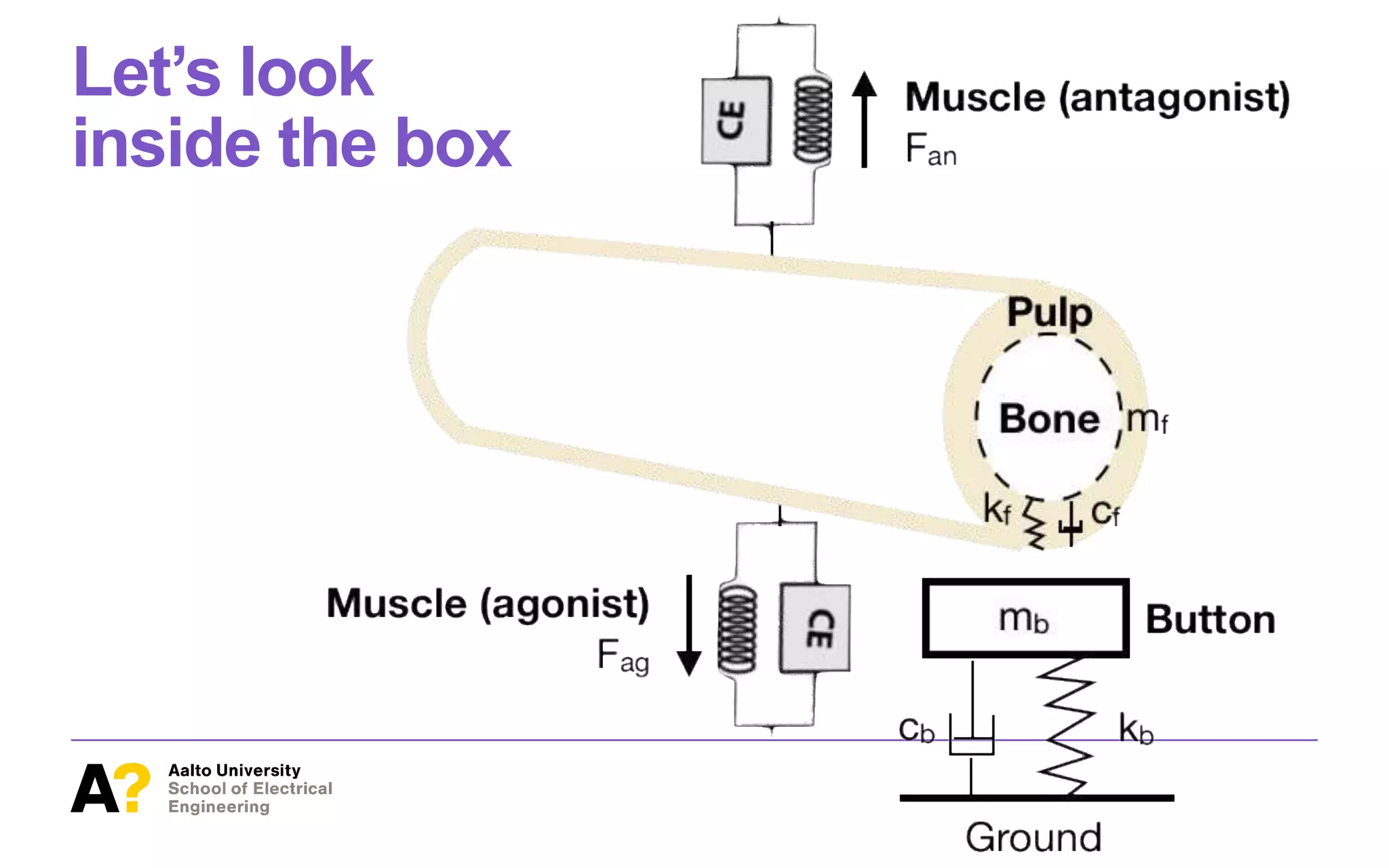
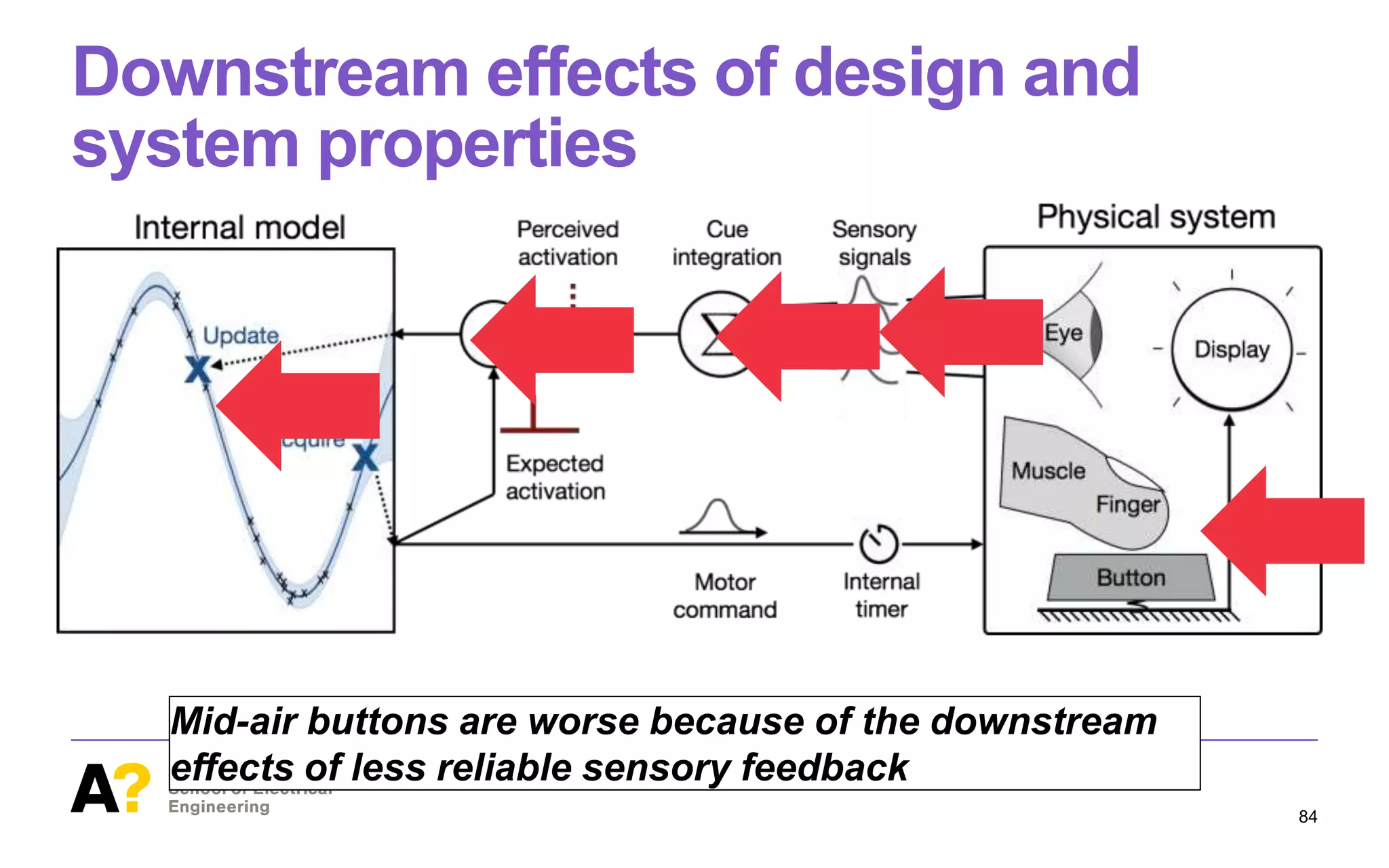
![The problem posed to the brain
Pressing a button requires careful timing and
proportioning of force.
The brain should be able to predict how to press a
new button and, if it fails, how to repair
A DOF problem + A prediction problem
NEUROMECHANIC (written in SMALL CAPS to distinguish from
neuromechanics, thetheory) isacomputational implementa-
tion of these ideas. It can be used asa modeling workbench
for comparing button designs. Its predictions approach an
upper limit bounded by neural, physical, and physiological
factors. Simulating presseswith arangeof button types(linear,
tactile, touch, mid-air), we find evidence for the optimality
assumption. Wereport simulation resultsfor (1) displacement–
velocity patterns, (2) temporal precision and success rate in
button activation, and (3) use of force, comparing with effects
reported in empirical studies [7, 33, 37, 40, 42, 47, 48, 53,
59, 61]. We show how the objective function can be tuned
to simulate a user prioritizing different task goals, such as
activation success, temporal precision, or ergonomics.
Whilethe model isan order of magnitude morecomplex than
thefamiliar approaches, it bears an important benefit: parame-
ter settings arerobust over arangeof phenomena. Thesimula-
tionswerecarried out by changing physically andanatomically
determined parameters, whilekeeping other model parameters
fixed without fitting them to human data. We discuss future
work to extend theapproach to morecomplex domains.
PRELIMINARIES: PARAMETERS OF BUTTON DESIGN
We introduce key properties of three main types of buttons:
physical, touch, and mid-air. This serves as background for
mechanical modeling of buttons in NEUROMECHANIC. We
herefocus on design parameters and postpone discussion of
empirical findings on button-pressing to Simulations.
For thepurposes of this paper, wedefineabutton asan elec-
tromechanical device that makes or breaks a signal when
pushed, then returns to itsinitial (or re-pushable) statewhen
released. It converts a continuous mechanical motion into a
discrete electric signal. Physical keyswitches and touch sen-
sors are common in modern systems. Physical dimensions
(width, slant, and key depth), materials (e.g., plastics), and
TACTILE PUSH-BUTTONS Tactileand “clicky” buttonsoffer more
points of interest (POIs), or changes during press-down and
release. F(B) is called actuation force, which is considered
the most important design parameter. dF(B − C)/F(B) is
called snap ratio and determines the intensity of tactile feel-
ing or ’bump’ of a button. A snap ratio greater than 40% is
recommended for astrong tactilefeeling by rubber-domeman-
ufacturing companies. Most POIsaretunable, yet somepoints
are dependent on other points. With some tactile buttons, a
distinct audible “click” sound may be generated, often near
the snap or makepoints.
TOUCH BUTTONS Touch buttonscan beconsidered azero-travel
button. Consequently, they show lower peak force than physi-
cal buttons do. Because of false activations, thefinger cannot
rest on the surface. Activation is triggered by thresholding
contact area of the pulp of thefinger on thesurface.
MID-AIR BUTTONS Mid-air buttonsarebased not on electrome-
chanical sensing but, for example, on computer vision or elec-
tromyographic sensing. Sincethey arecontactless, they do not
have a force curve. The point of activation is determined by
reference to angle at joint or distance traveled by the fingertip.
Latency and inaccuracies in tracking are known issues with
mid-air buttons.
Figure2. Idealized force–displacement curvesfor linear (left) and tactile
(right) buttons. Green lines are press and blue lines are release curves.
Annotations (A–H) arecovered in thetext.
2
But buttons are black boxes!
Force-displacement curves
of two buttons](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-72-2048.jpg)

![Oulasvirta et al. Proc. CHI 2018
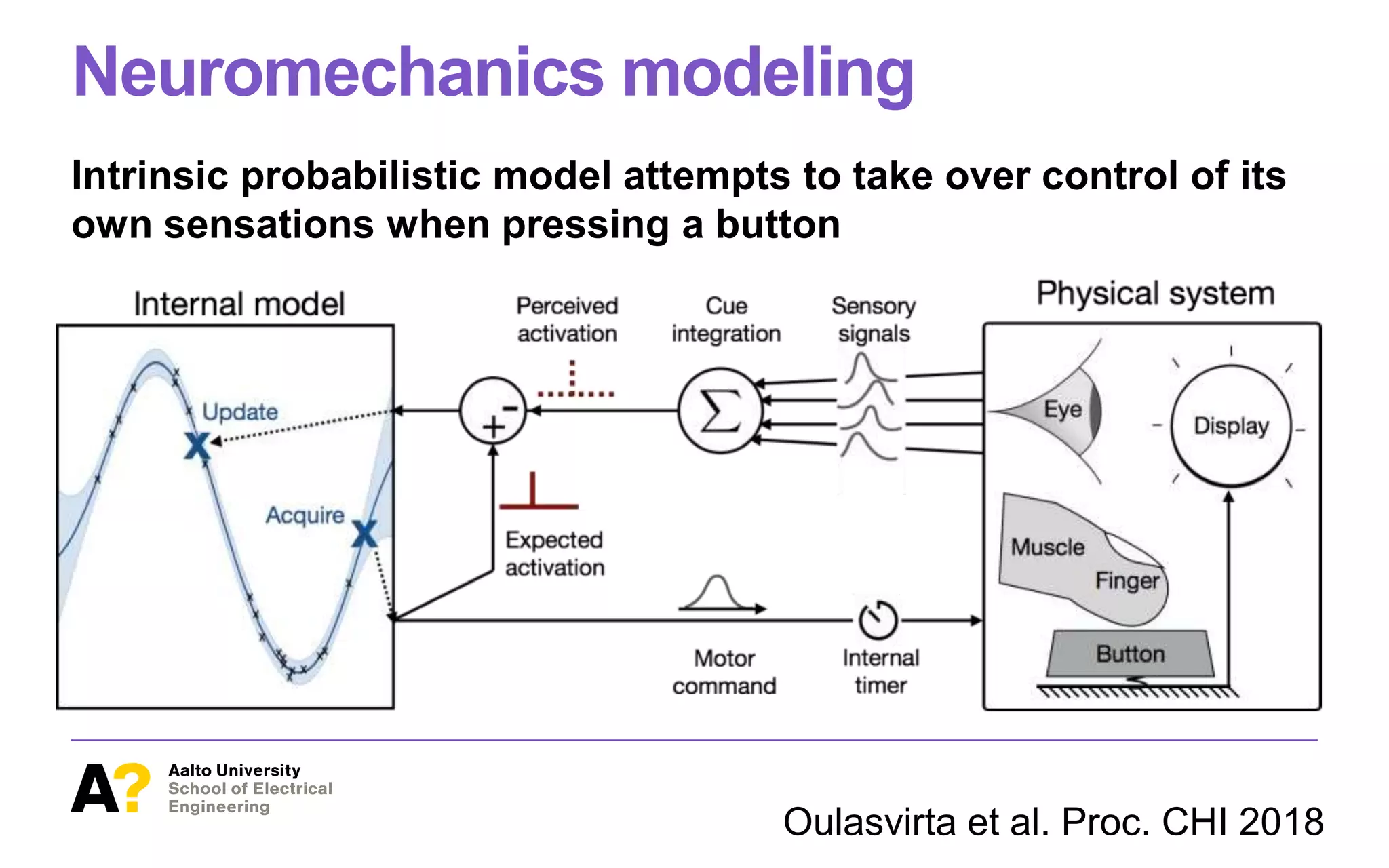
Neuromechanics modeling
Figure4. NEUROM ECHANI C isa computational model of neuromechanicsin button-pressing. It implementsaprobabilistic internal model (Gaussian
process regression) that attempts to minimize error between its expected and perceived button activation. Its motor commands are transferred via a
noisy and delayed neural channel to muscles controlling the finger. A physical simulation of thefinger acting on thebutton yields four types of sensory
signals that areintegrated into a singlepercept (p-center) by meansof a maximum likelihood estimator.
NEUROMECHANIC: A COMPUTATIONAL MODEL
NEUROMECHANIC implements these ideascomputationally. It
consists of two connected sub-models (Figure 4).
Objective Function
A motor command q sent to the finger muscles consists of
three parameters:
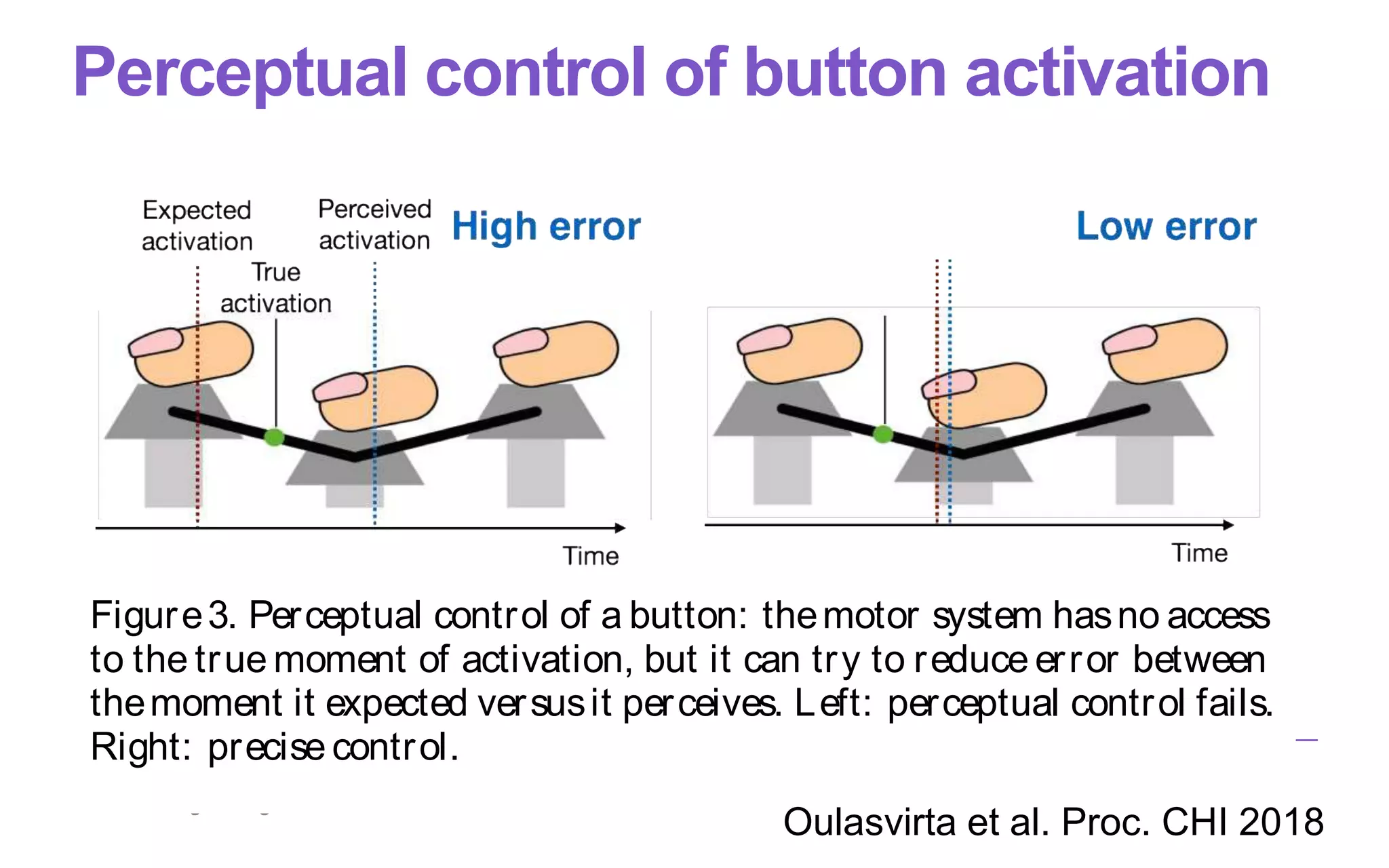
of p-Centers
nnected to four extero-
oprioception, audition,
oduces ap-center pci.
aneural signal evoked
ceptors. We are espe-
tors on the finger pad
abutton press. Slowly
to coarse spatial struc-
surfaceof thebutton),
ond to motion. Kim
als from the fingertip
d jerk from the finger
and indentation have
correlates highly with
use buttons havelittle
odel to mechanorecep-
ime-varying signal is
sitivecomponents. In
for estimating pco isaweighted average [16, 17]:
pco = Â
i
wi pci where wi =
1/ s 2
i
Âi 1/ s 2
i
(7)
with wi being theweight given to theith single-cue estimate
and s 2
i being that estimate’s variance. Figure 6 shows ex-
emplary p-center calculations: signal-specific (pci) and inte-
grated p-centers (pco) from 100 simulated runs of NEUROME
CHANIC pressing a tactile button. Note that absolute differ-
ences among pci do not affect pco, only signal variances do
The integrated timing estimate isrobust to long delays in, say
auditory or visual feedback. This assumption is based on a
study showingthat physiological eventsthat takeplacequickly
within a few hundred milliseconds, do not tend to be cause
over- nor underestimations of event durations [14].
IMPLEMENTATION AND PARAMETER SELECTION
NEUROMECHANIC is implemented in MATLAB, using
BAYESOPT for Bayesian optimization (GP model uses the
ARD Matern 5/2 kernel), SIMSCAPE for mechanics, and
nicsin button-pressing. It implementsaprobabilistic internal model (Gaussian
d and perceived button activation. Its motor commands are transferred via a
ysical simulation of thefinger acting on thebutton yields four typesof sensory
maximum likelihood estimator.
Objective Function
A motor command q sent to the finger muscles consists of
threeparameters:
q = { µA+ ,t A+ ,sA+ } (1)
pressing. It implementsaprobabilistic internal model (Gaussian
d button activation. Its motor commands are transferred via a
on of thefinger acting on thebutton yieldsfour typesof sensory
ihood estimator.
ve Function
or command q sent to the finger muscles consists of
arameters:
q = { µA+ ,tA+ ,sA+ } (1)
gnal offset µ, signal amplitudet , and duration s of the
(A+) muscle. Wehaveset physiologically plausible
a(min and max) for theactivation parameters.
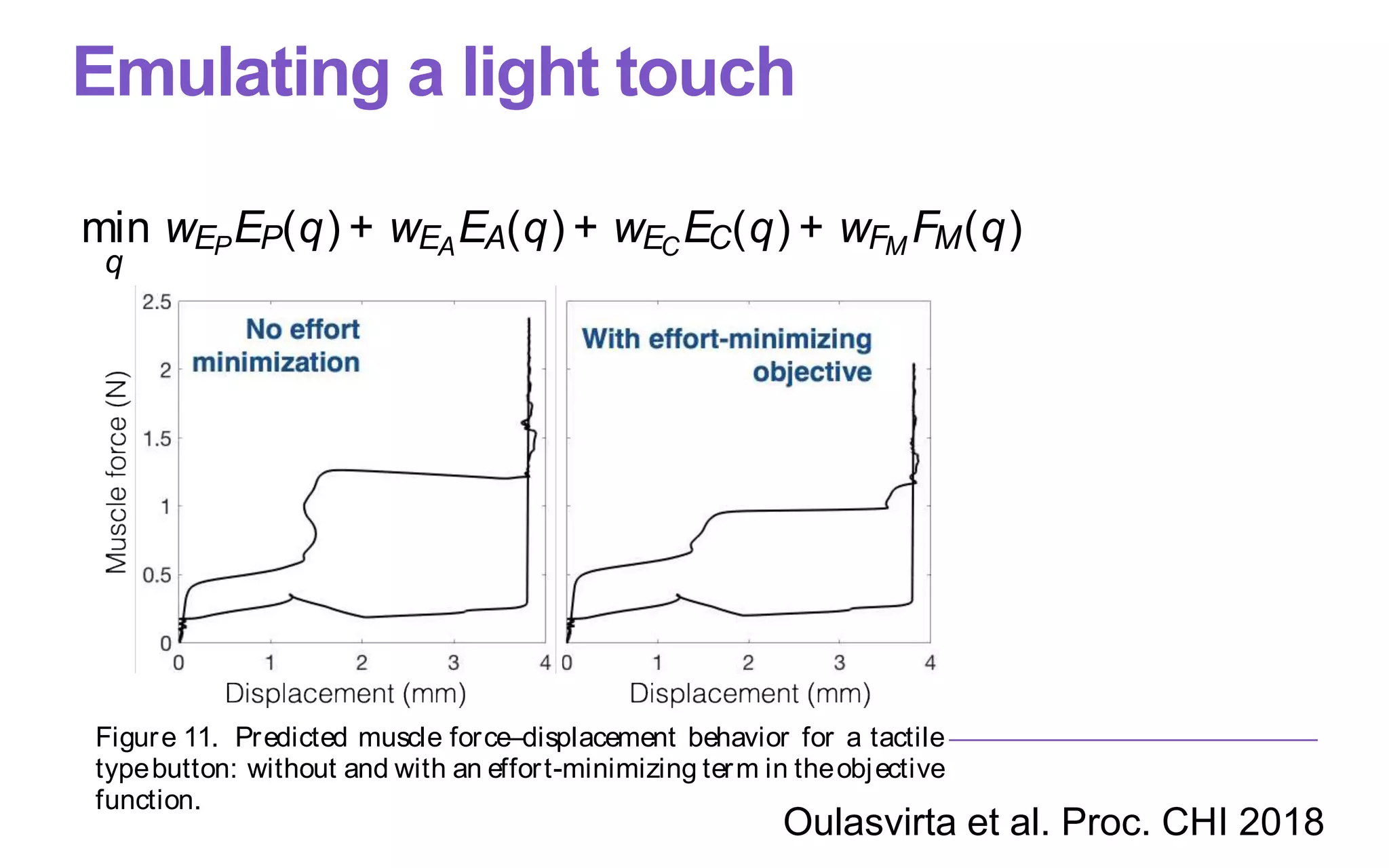
ectiveisto determine q that minimizes error:
min
q
EP(q) + EA(q) + EC(q) (2)
EP is error in predicting perception, EA is error in ac-
thebutton, and EC iserror in making contact (button
touched). Weassumethat activation and contact errors](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-78-2048.jpg)
![ParametersTable 1. Model parameters. Button parameters here given for physical
buttons. Task parameters (e.g., finger starting height) are given in text.
f denotes function
Variable Description Value, Unit Ref.
fr Radius of finger cone 7.0 mm
fw Length of finger 60 mm
r f Density of finger 985 kg/m3
cf Damping of finger pulp 1.5 N·s/m [64]
kf Stiffness of finger pulp f , N/m [65]
wb Width of key cap 14 mm
db Depth of key cap 10 mm
r b Density of key cap 700 kg/m3
cb Damping of button 0.1 N·s/m
ks Elasticity of muscle 0.8·PCSA [38]
kd Elasticity of muscle 0.1·ks [38]
kc Damping of muscle 6 N·s/m [38]
PCSA Phys. cross-sectional area 4 cm2
L0ag, L0an Initial muscle length 300 mm
sn Neuromuscular noise 5·10− 2
sm Mechanoreception noise 1·10− 8
s p Proprioception noise 8·10− 7
sa Sound and audition noise 5·10− 4
sv Display and vision noise 2·10− 2
Figure 7. Data collection on press kinematics: A single-sub
High-fidelity optical motion tracking was used to track a m
the finger nail. A custom-made single-button setup was cre
switches and key capsfrom commercial keyboards.
SIMULATIONS: COMPARING BUTTON DESIGNS
We investigated NEUROMECHANIC in a series of sim
addressing four button types: tactile, linear, touch, an
The tactile button type is one of the most commo
in commercial keyboards. The linear type is a cha
case, because theonly difference isthe ’tactile bump
buttons, on theother hand, arecommon and generall
ered worse than physical button. Mid-air buttons, on
hand, lack mechanoreceptive feedback entirely and
proprioceptivefeedback.
We inspect predictions for displacement–velocity
force–displacement curves, muscle forces, as wel
level measures (perceptual error and button activation
Except for neural
noise parameters,
all parameters are
physically
measurable or
known.
Button-pressing
behavior emerges](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-79-2048.jpg)
![Example result: Force-velocity curves
omics.
complex than
nefit: parame-
a. Thesimula-
anatomically
el parameters
discuss future
omains.
DESIGN
es of buttons:
ckground for
CHANIC. We
discussion of
ions.
on asan elec-
signal when
e) state when
motion into a
nd touch sen-
l dimensions
plastics), and
cal buttons do. Because of false activations, thefinger cannot
rest on the surface. Activation is triggered by thresholding
contact area of thepulp of thefinger on the surface.
MID-AIR BUTTONS Mid-air buttons arebased not on electrome-
chanical sensing but, for example, on computer vision or elec-
tromyographic sensing. Sincethey arecontactless, they do not
have aforce curve. The point of activation is determined by
reference to angle at joint or distance traveled by thefingertip.
Latency and inaccuracies in tracking are known issues with
mid-air buttons.
Figure2. Idealized force–displacement curvesfor linear (left) and tactile
(right) buttons. Green lines are press and blue lines are release curves.
Annotations (A–H) arecovered in the text.
2
LINEAR
ysical
n text.
Ref.
[64]
[65]
Figure 7. Data collection on press kinematics: A single-subject study.
High-fidelity optical motion tracking was used to track a marker on
Oulasvirta et al. Proc. CHI 2018](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-80-2048.jpg)












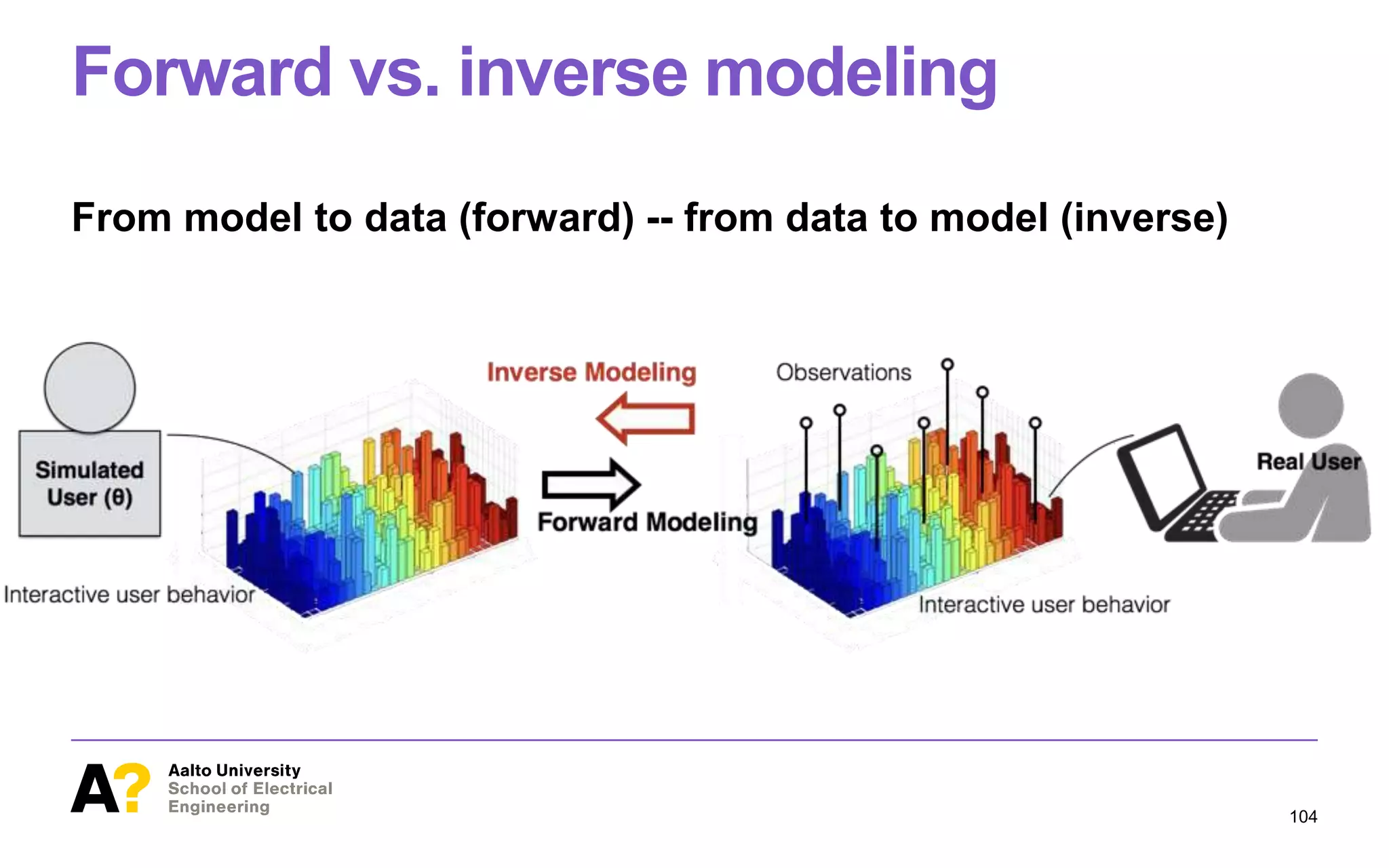


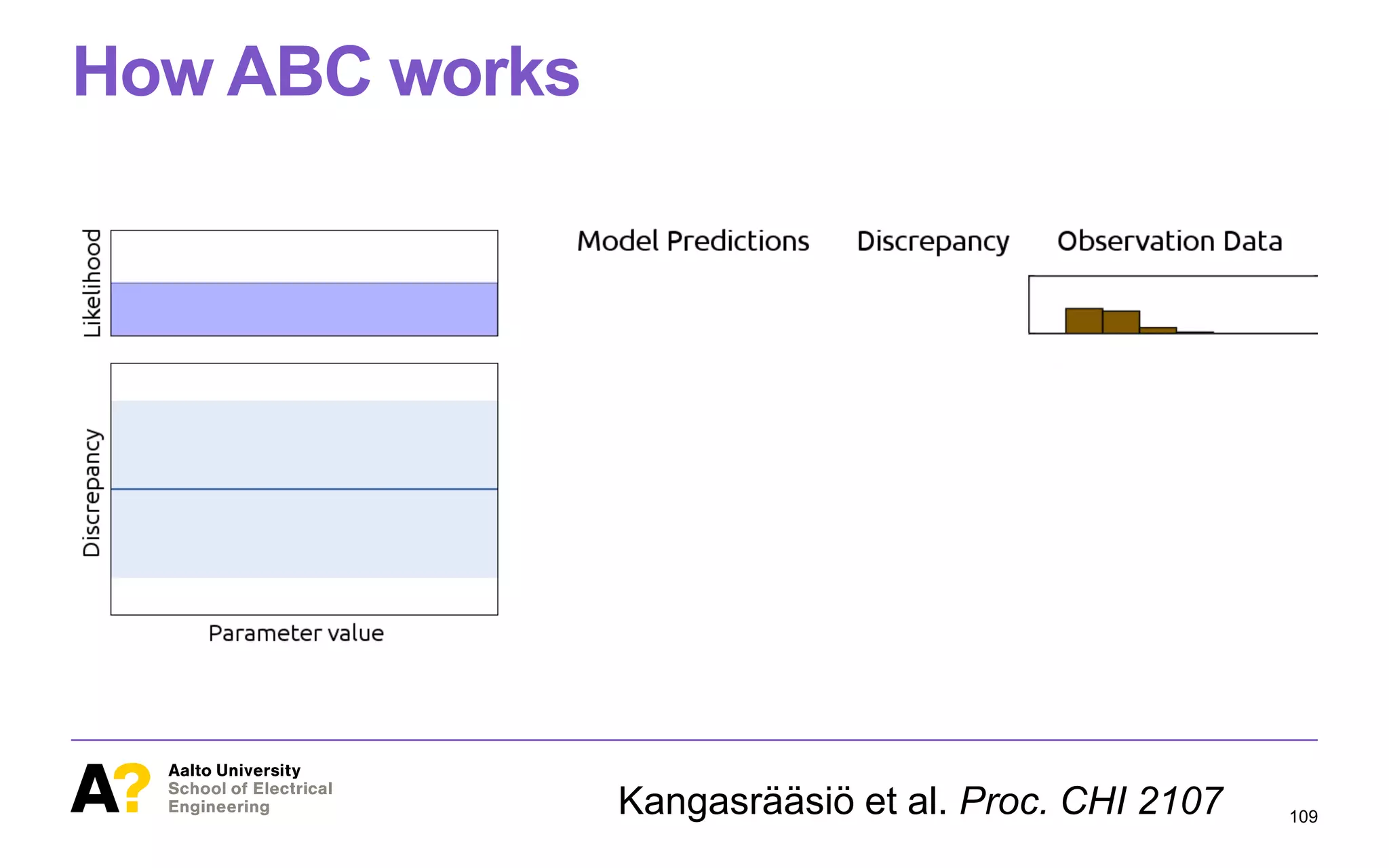
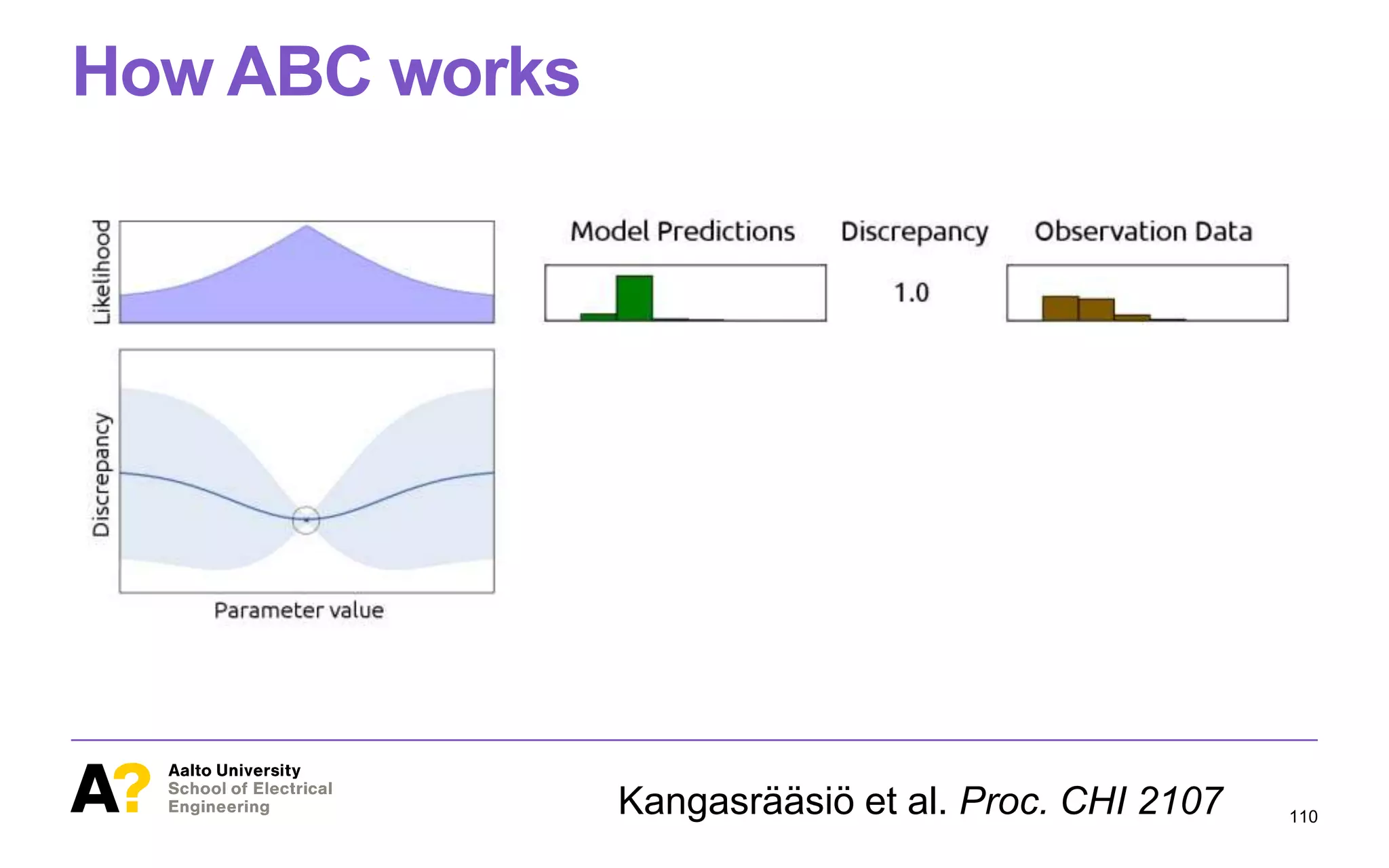
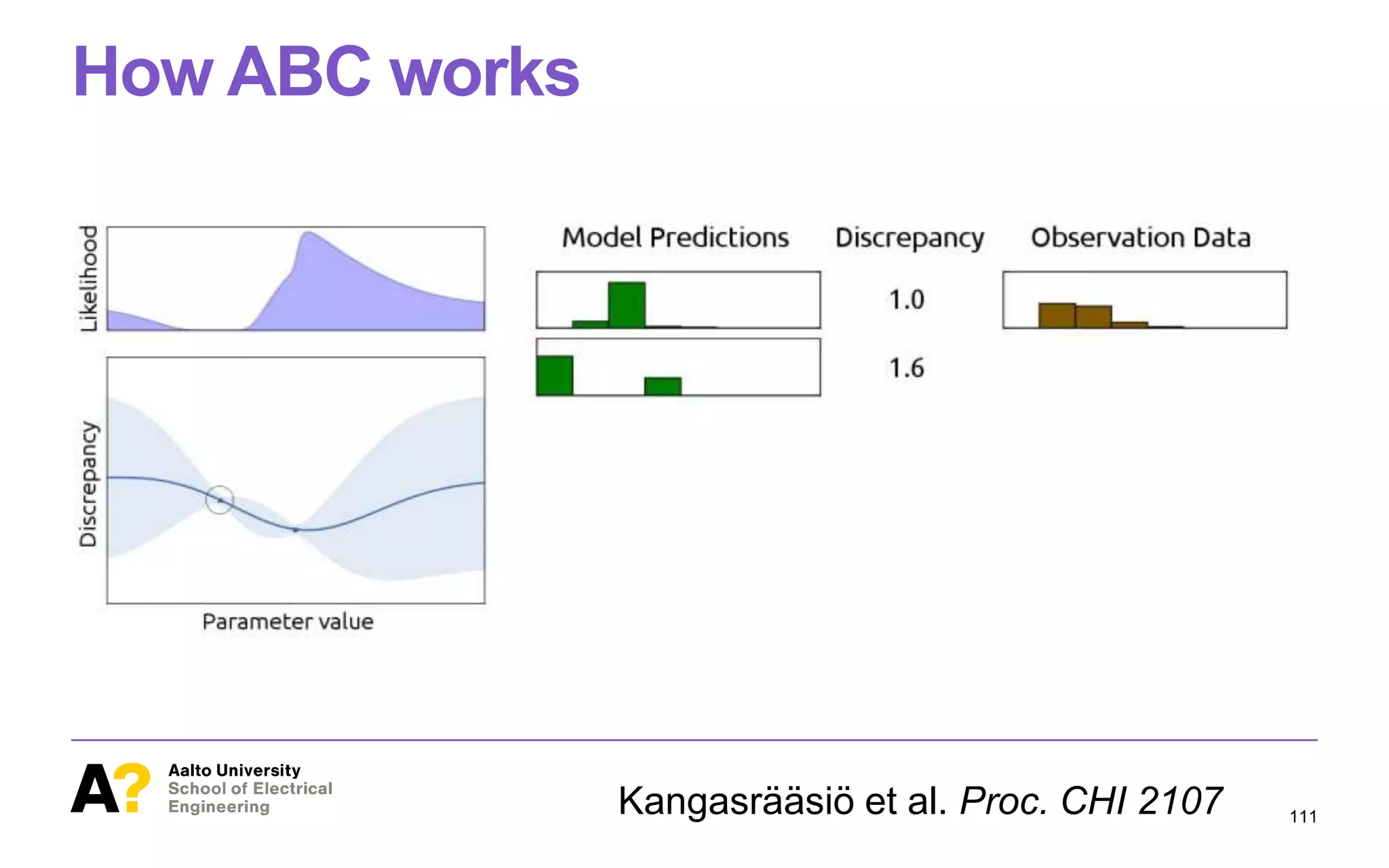
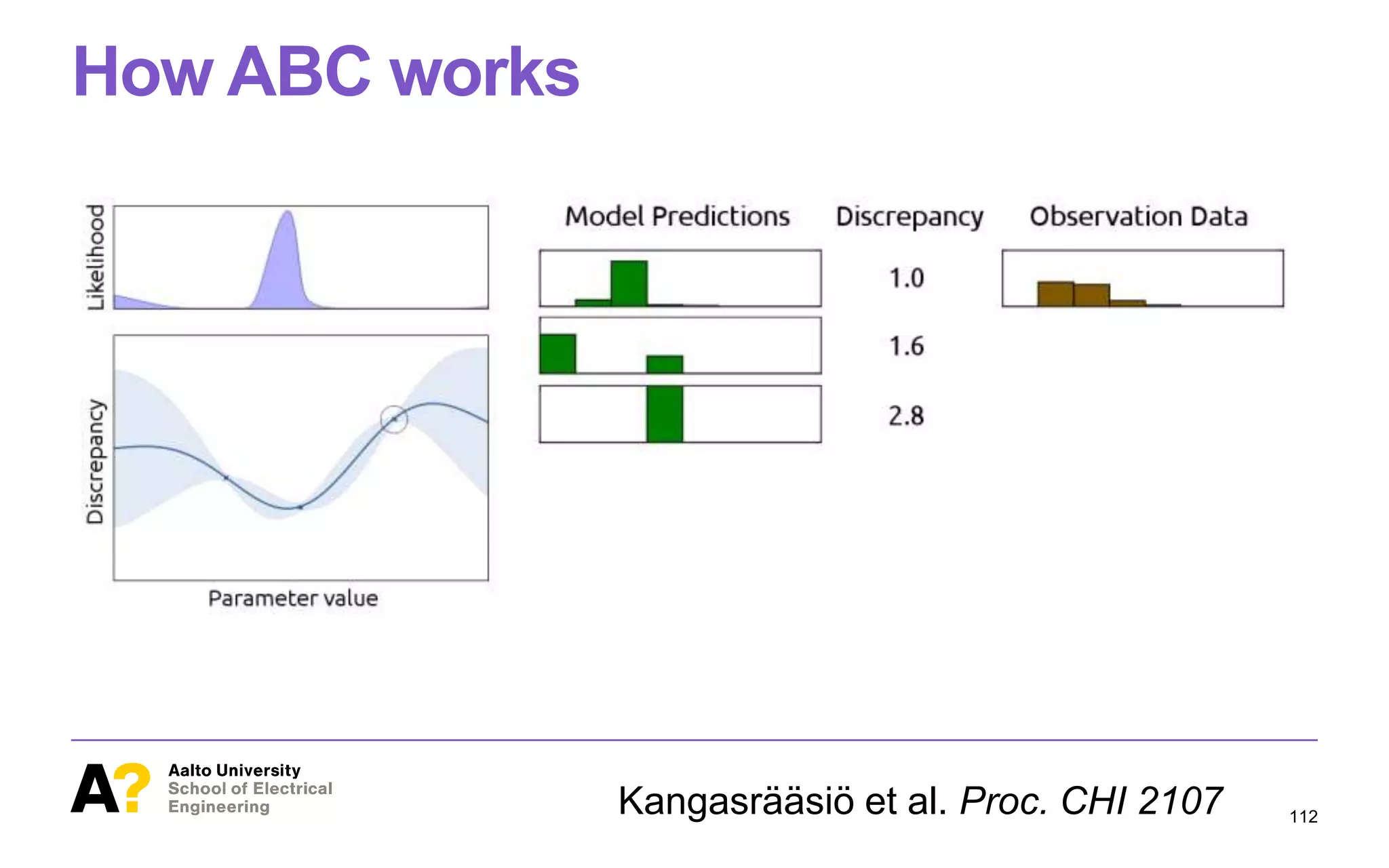
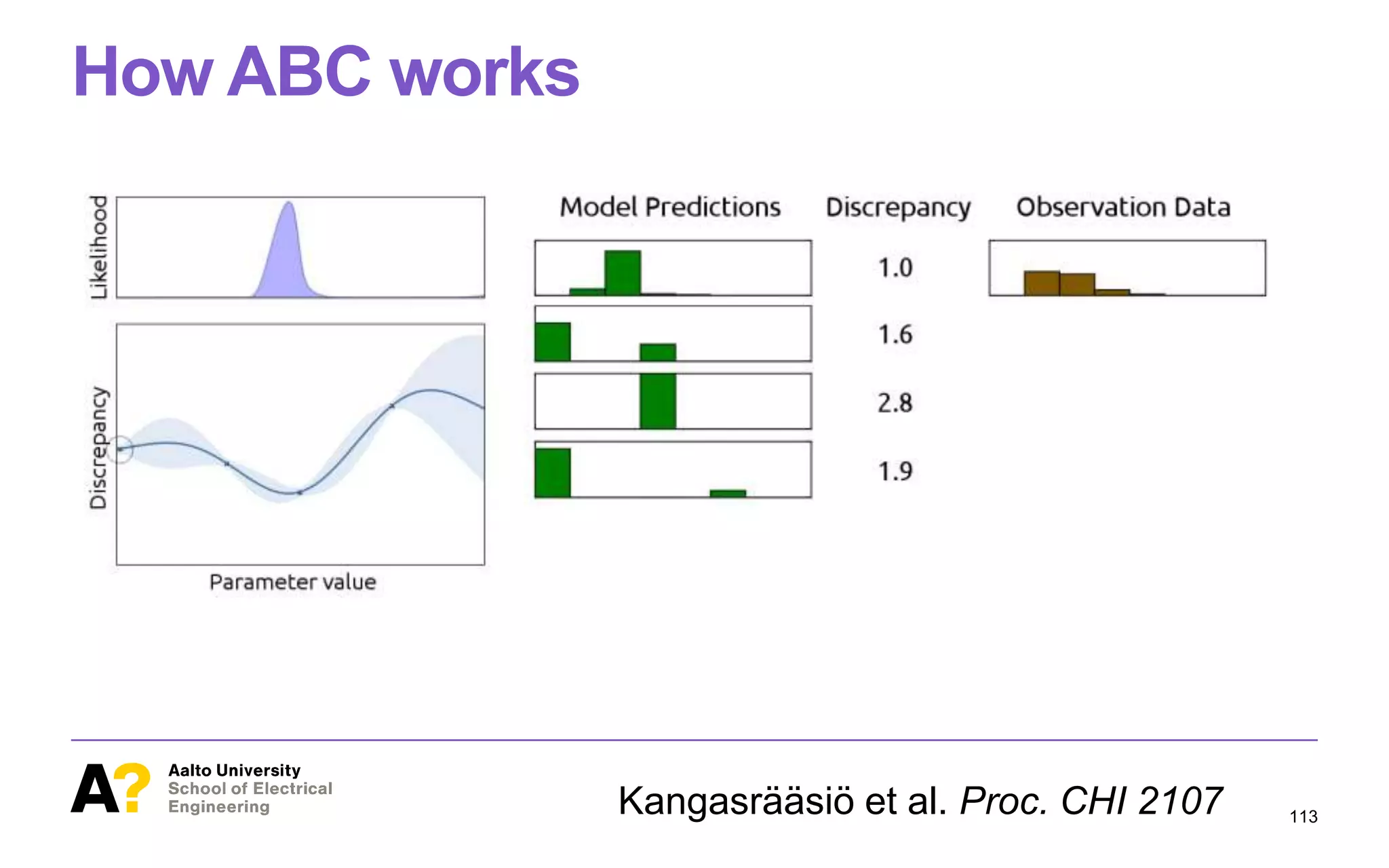
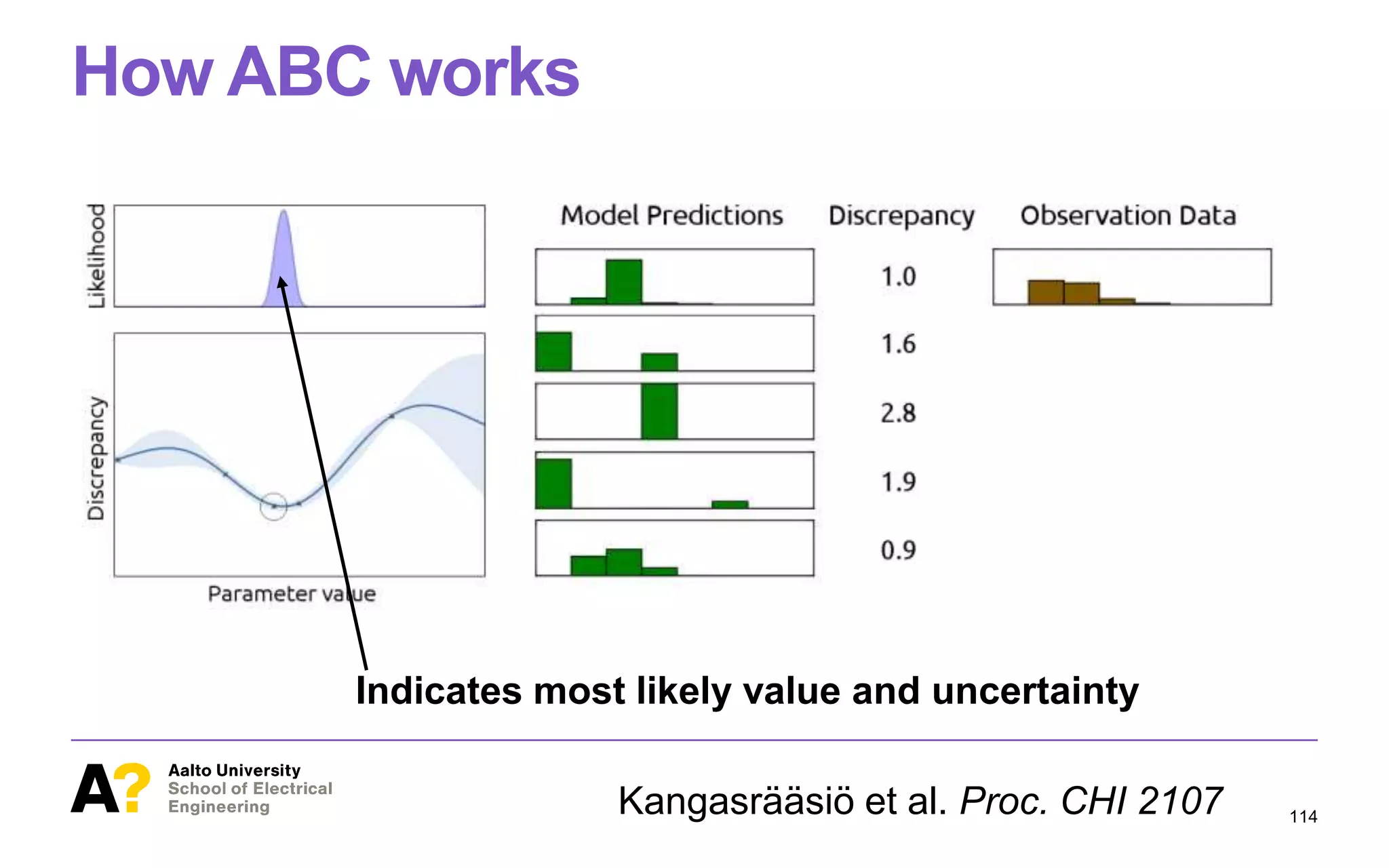
![ABC is a principled way to find optimal
model parameters
Figure 1. This paper studies methodology for inference of parameter
values of cognitive models from observational data in HCI. At the bot-
tom of the figure, we have behavioral data (orange histograms), such as
task solution, only the objecti
straints of thesituation, weca
theoptimal behavior policy. H
that isinferring theconstraints
optimal, isexceedingly difficu
quality and granularity of pre
this inversereinforcement lear
to beunreasonable when often
data exists, such as isoften the
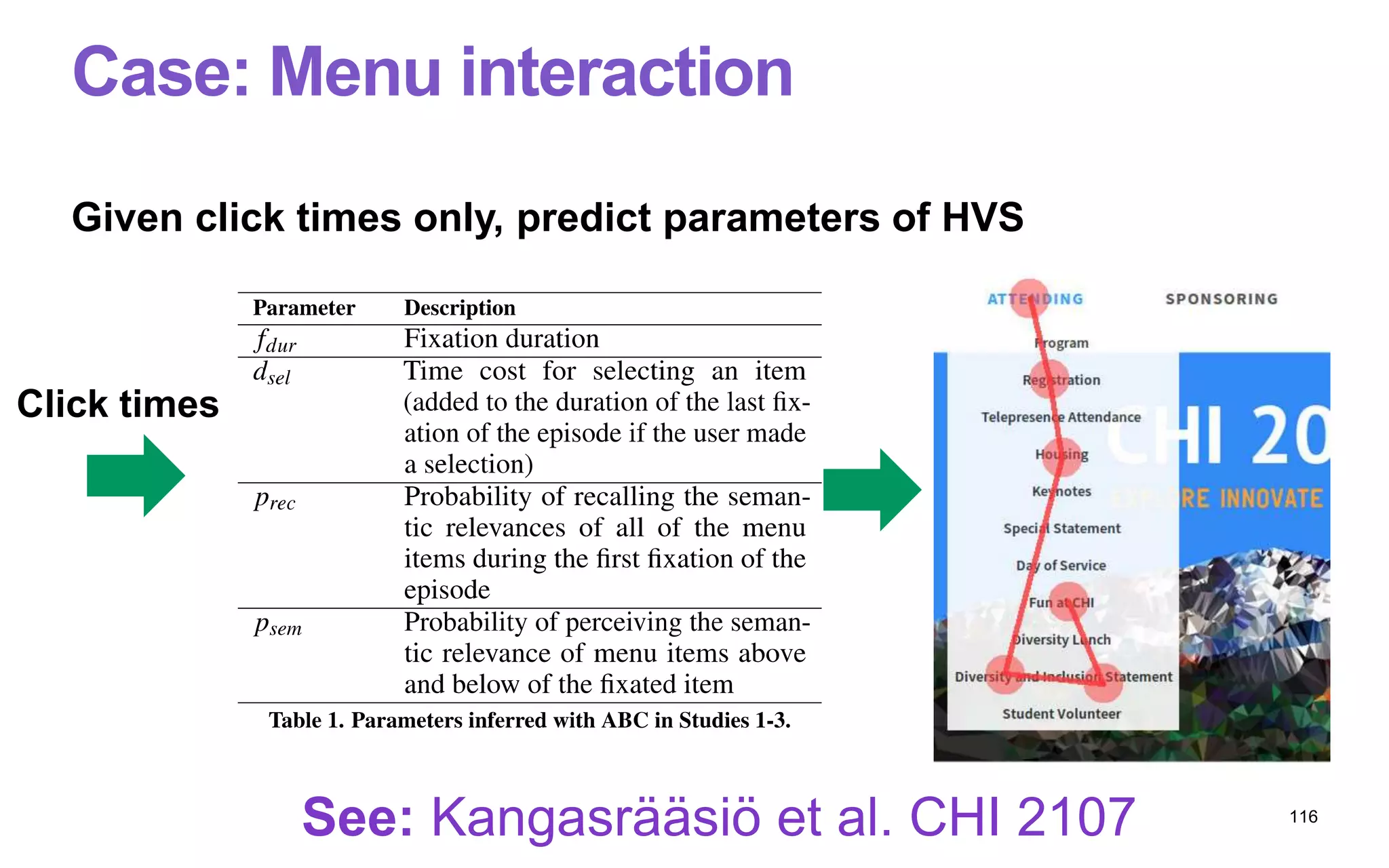
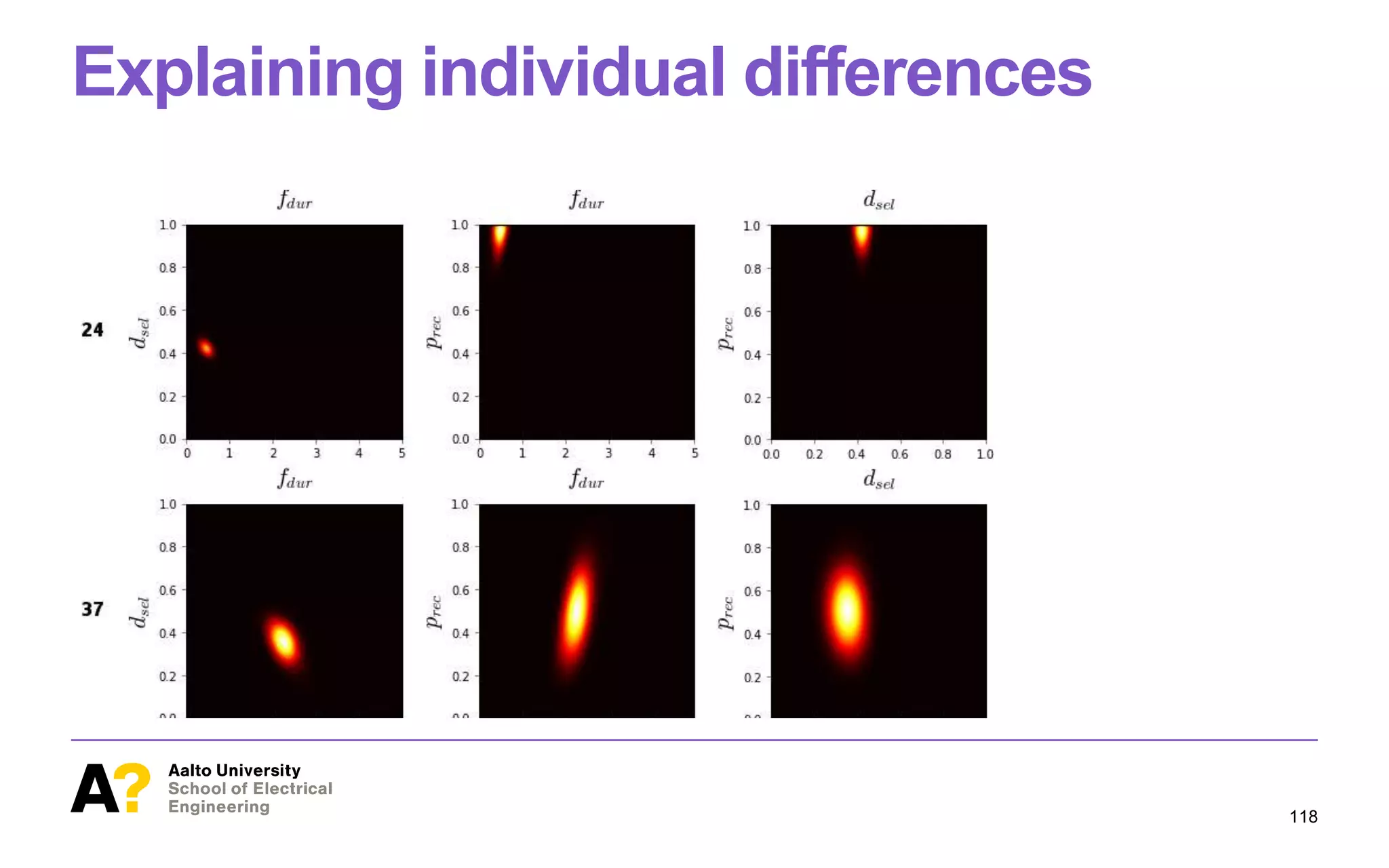
Our application case is a rece
[13]. The model studied here
tation of search behavior, and
completion times, in varioussi
parametric assumptions about
visual system (e.g., fixation dur
Kangasrääsiö et al. Proc. CHI 2107](https://image.slidesharecdn.com/computational-rationality-i-oulasvirta-march-12-2018-180312173249/75/Computational-Rationality-I-a-Lecture-at-Aalto-University-by-Antti-Oulasvirta-107-2048.jpg)