More Related Content
PDF
PDF
2015-09-02 @ 大型実験施設とスーパーコンピュータとの連携利用シンポジウム PPTX
CMSI計算科学技術特論C (2015) feram と強誘電体① PDF
CMSI計算科学技術特論C (2015) xTAPP をはじめとしたDFT コードと PDF
CMSI計算科学技術特論C (2015) feram と強誘電体② PDF
密度汎関数法, Density Fuctional Theory (DFT)の基礎第5回 PDF
PPTX
More from dc1394
PDF
Pseudopotential of vanderbilt PDF
Development of highly accurate pseudopotential method and its application to ... PDF
A lda+u study of selected iron compounds 第一章 PDF
PDF
水素原子に対するSchrödinger方程式の数値解法 PDF
PDF
PDF
PDF
PDF
SchracVisualizeによる波動関数の可視化 PDF
A lda+u study of selected iron compounds 第二章 PDF
PDF
PDF
単振り子と二重振り子のコンピュータシミュレーション PDF
PDF
Troullier and Martinsの擬ポテンシャルの作成法 高精度擬ポテンシャル法の開発と表面系への応用
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
なぜZrB2なのか
有用な特性
高い硬度(モース硬度8)
高融点性(2400℃)および金属性伝導率(熱伝導率99 (W/mK)、電気
抵抗4.6 (μΩ/cm))
期待される用途
電子エミッタ
触媒
(例えば、青色LEDなどの光学機器に使用される)GaNの薄膜結晶成
長のための基板
実際に、Tolleらによって、Si基板の上に成長したZrB2層が、
GaNの薄膜結晶成長のための、非常によい鋳型を提供する
ことが発見された。
我々はこの実験の過程で、Si基板の上のZrB2層のさらに上に、
Si基板のSi原子が移動して単一層を作ることを発見した。
J. Tolle et al., Appl. Phys. Lett. 84, 3510 (2004)
- 13.
- 14.
- 15.
- 16.
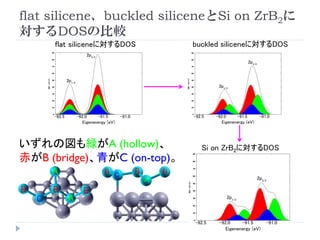
Si on ZrB2の構造
Si原子の位置A (hollow) B (bridge) C (on-top)
ZrB2表面からの距
離(平均)
2.124 (Å) 3.062 (Å) 2.727 (Å)
最近接Zr原子との
距離(平均)
2.815 (Å) 3.216 (Å) 2.684 (Å)
最近接Si原子との
距離(平均)
2.266 (Å) 2.258 (Å) 2.242 (Å)
最近接Si原子と作
る角度(平均)
104.1°
(sp3 like)
109.7°
(intermediate)
117.8°
(sp2 like)
- 17.
- 18.
- 19.
- 20.
SiliceneのDirac cone
flatsiliceneにはDirac coneが明らかに存在する。
しかし、buckled siliceneはDirac coneが壊れている。
flat siliceneのバンド構造 buckled siliceneのバンド構造
- 21.
- 22.
- 23.
- 24.
- 25.