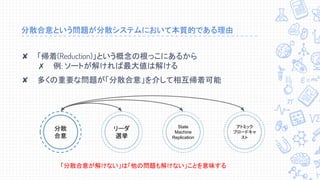
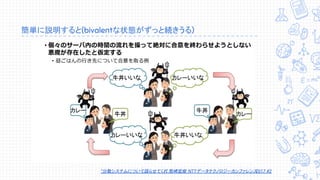
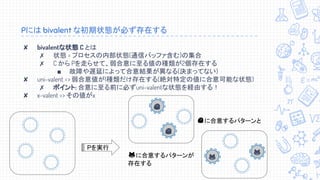
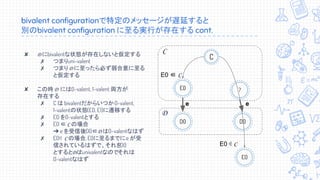
↓↓↓↓訂正あります。↓↓↓↓
2018/07/02に株式会社エフコード社内で行われた勉強会のスライドです。
訂正版(随時更新中): https://docs.google.com/presentation/d/15HOMfAbtdWwO48njcB8IdkN3kVAMu3wsmZo0O3S-f_4/edit?usp=sharing
専門家による資料・専門家向けの資料ではありません。自分自身で学習し、論文・文献等を読解してまとめた内容となります。間違い等あるかもしれませんが、あれば是非コメント頂ければと思います。
【訂正事項】
スライド16:
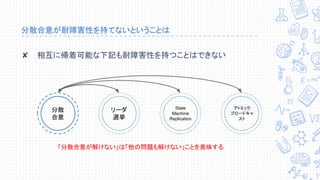
誤:たった一つのプロセスが故障しただけでも有限時間で合意できない
正:たった一つのプロセスが故障しうるだけでも有限時間で合意できない
スライド20:
誤: 重要: あるschedule σ1, σ2 がdisjoint (nodeが被ってない) なら可換
正: 重要: あるschedule σ1, σ2 がdisjoint (processが被ってない) なら可換
スライド24, 34
誤: “分散システムについて語らせてくれ” 熊崎宏樹 NTTデータテクノロジーカンファレンス2017 #2
正: “分散システムについて語らせてくれ” 熊崎宏樹 NTT Tech Conference #2