日本語形態素解析入門

1. 日本語形態素解析入門 ver.0.3 updated 2009-01-27

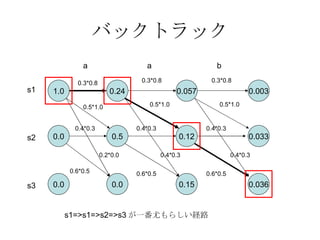
2. はじめに 本資料の作成に辺り以下のサイト ( アーティクル ) を参考にさせていただきました。 日本語形態素解析入門 [ 山下達雄 ] http://nais.to/~yto/doc/tech/jma/jma19990514.pdf Double-Array Articles [ 矢田 晋 ] http:// nanika.osonae.com/DArray / 確率的言語モデルによる自由発話認識に関する研究 [ 村上仁一 ] http://unicorn.ike.tottori-u.ac.jp/murakami/doctor/

3. 目次 形態素解析とは 形態素解析の仕組み 形態素辞書探索 形態素間の接続可能性の確認 最適解探索

4. 形態素解析とは 入力 文字列 出力 形態素の列 形態素解析をざっくり説明 与えられた文字列を形態素に分解(複数候補) 上の候補から一番もっともらしいものを出力 入力：東京都 候補：東京都(名詞), 東京(名詞)-都(名詞), 東(名詞)-京都(名詞) 出力：東京都(名詞)

5. 形態素解析の必要性 情報検索 日本語分ち書き N-gram 形態素解析 なぜ形態素解析を利用するか N-gram に比べて precision( 正答率 ) が高い 2-gram の例 ( 東京都 => 東京 , 京都 ) でもめんどくさい (‘A`) 言語依存性 日本語形態素解析システムは中国語に利用できない 新語に弱い

6. 目次 形態素解析とは 形態素解析の仕組み 形態素辞書探索 形態素間の接続可能性の確認 最適解探索

7. 形態素解析の仕組み 形態素解析は以下の3つに分けられる 形態素辞書探索 “涼宮ハルヒ”が辞書に存在するか？ 形態素間の接続可能性の確認 名詞の直後に動詞が出現するか？ 最適解探索 一番尤もらしい形態素の列はなにか？

8. 目次 形態素解析とは 形態素解析の仕組み 形態素辞書探索 形態素間の接続可能性の確認 最適解探索

9. 形態素辞書探索 辞書探索の必要性 分割候補は文字列長の２のべき乗通り 辞書を使用することで候補数を抑える 涼宮ハルヒ => {(涼,宮,ハ,ル,ヒ), (涼,宮,ハ,ルヒ), (涼,宮,ハル,ヒ),(涼,宮,ハルヒ), (涼,宮ハ,ル,ヒ),(涼,宮ハ,ルヒ), (涼,宮ハル,ヒ), (涼,宮ハルヒ) , (涼宮,ハ,ル,ヒ), (涼宮,ハ,ルヒ), (涼宮,ハル,ヒ), (涼宮,ハルヒ), (涼宮ハ,ル,ヒ), (涼宮ハ,ルヒ), (涼宮ハル,ヒ), (涼宮ハルヒ)} 合計2^4通り！

10. 形態素辞書探索 辞書探索には以下のような文字列探索アルゴリズムが用いられる Common Prefix Search Double Array Trie PAT 木 Suffix Array Trie + NDBM AC 法 (Aho-Corasick 法 ) Trie を用いた CommonPrefixSearch

11. Double Array Trie Trie 概要 Trie のデータ構造 Double Array 概要 Double Array Trie による文字列探索

12. Trie 概要 Trie とは文字列探索 (reTRIEval) のためのデータ構造 (DFA の一種 ) “ bird”, “bison”, “cat”, “birdie” を格納する Trie

13. Trie のデータ構造 Trie は抽象的なデータ構造なので実装のためにはより具体的なデータ構造を考える リスト実装 ( 速度：遅 , 領域：小 ) 配列実装 ( 速度：速 , 領域 : 大 ) Double 配列実装 ( 速度：速 , 領域：小 )

14. Double Array概要 Double Arrayは小さい領域で高速な実装 2つの配列BASEとCHECKを用いてデータを格納する 節 x から節 y に至る文字 c に対応する枝が存在するとき BASE[x]+CODE[c]=y x = CHECK[y] が成り立つ。 また , x が葉  BASE[x] < 0

15. Double Array Trie による文字列探索 “bird”を検索 BASE[1]+CODE[‘b’] = 4, CHECK[4]=1 BASE[4]+CODE[‘i’] = 7, CHECK[7]=4 BASE[7]+CODE[‘r’] = 10, CHECK[10] = 7 BASE[10]+CODE[‘d’] = 6, CHECK[6] = 10 BASE[6] + CODE[‘#’] = 2, CHECK[2]=6 BASE[2] < 0 “bird” が見つかった！！

16. 目次 形態素解析とは 形態素解析の仕組み 形態素辞書探索 形態素間の接続可能性の確認 最適解探索

17. 接続可能性の確認 連続する形態素が接続するか、どれだけ接続しやすいか mecab では 2 次元のテーブル (matrix) を用意して連接コスト探索を行う

18. 目次 形態素解析とは 形態素解析の仕組み 形態素辞書探索 形態素間の接続可能性の確認 最適解探索

19. 最適解探索 最適解探索の方法は以下のようなものが存在 左最長一致法 形態素数最小法 2文節最長一致法 コスト最小法 確立モデル

20. コスト最小法 文字列”さかなだよ”に対する辞書探索結果 さ - かな - だ - よ さか - なだ - よ さかな - だ - よ 上記各候補に生起コスト , 連接コストを付与 さ (100)-(30) かな (200)-(30) だ (10)-(30) よ (10) さか (200)-(30) なだ (200)-(45) よ (10) さかな (200)-(30) だ (10)- よ (10)

21. コストの定義 生起コスト, 連接コストを定義する 人手による定義 コーパスを利用して, 統計的に推定

22. 確立モデルを用いたコスト計算 形態素解析は以下の関数を最小化する W={w1,...,wn}, T={t1,....,tn} を求めること また事後確立は出現確立と同時確立を用いて計算することができる。 wi:i 番目の単語 ti:i 番目の単語の品詞

23. コーパス中で名詞が１００回, 名詞の直後に動詞が３０回, “さかな”が5回出現した場合 さ (0.02)-(0.1) かな (0.01)-(0.1) だ (0.5)-(0.5) よ (0.5) さか (0.04)-(0.1) なだ (0.01)-(0.15) よ (0.5) さかな (0.04)-(0.1) だ (0.5)- よ (0.5)

24. 式 (2) が最小であるとき式 (1) は最大である。 確立が最大となる組を求めることはコストが最小となる組をみつけることに等しい！！ =>人手によるコストとコーパスでの確立をマージできる 生起コスト 連接コスト

25. Viterbi のアルゴリズム start end a b c e d g f 20 10 30 20 30 10 10 40 10 20 10 startからendまでの最もコストの低いパスを見つける startからendまでの最も確立の高いパスを見つける

26. Viterbi のアルゴリズム このアルゴリズムが解く問題 観測された系列に対し , 最適な状態系列を求める 既に以下のことがわかっている “ 晴れ” => 秋葉原でメイド喫茶に行く (70%) “ 晴れ” => 家でニコニコ動画を見る (30%) “ 雨” => 秋葉原でメイド喫茶に行く (40%) “ 雨” => 家でニコニコ動画を見る (60%) 晴れの確率 (70%) 前日が晴れのとき , 次の日が晴れの確率 (80%) 前日が雨のとき , 次の日が晴れの確率 (40%) 土曜日は家でニコニコ動画を見 , 日曜日は秋葉原のメイド喫茶に行った ( ということが観測された ) 土曜日 , 日曜日の天気は？ ( 尤もらしい状態の系列は？ )

27. Viterbi のアルゴリズム 次のようなオートマトンを考える. s1 s2 s3 0.2 a:0 b:1.0 0.3 a:0.8 b:0.2 0.5 a:1.0 b:0 0.4 a:0.3 b:0.7 0.6 a:0.5 b:0.5 状態 s1 から s2 に遷移する確率は 0.2 でこのとき、 a を出力する確率は 0, b は 1.

28. 前述のオートマトンが” abb” を出力する確率 “ aab” を出力する各状態系列の確率の総和 s1->s1->s1->s3 ((0.3*0.8)*(0.3*0.8)*(0.2*0.1) = 0.01152) s1->s1->s2->s3 ((0.3*0.8)*(0.5*1.0)*(0.6*0.5) = 0.036) s1->s2->s2->s3 ((0.5*1.0)*(0.4*0.3)*(0.6*0.5) = 0.018) “ aab” が出力されていたとき , 一番尤もらしい状態系列 s1->s1->s2->s3 ((0.3*0.8)*(0.5*1.0)*(0.6*0.5) = 0.036) Viterbi のアルゴリズム

29. Viterbi のアルゴリズム “ aab” が出力されていたとき , 一番尤もらしい状態系列を見つけるアルゴリズム

30. モデル λ において観測系列 に対する最 適な状態系列 を求めるために、時刻 t で状態 i に至るまでの 最適状態確率 を定義する。

31. 最適状態確率の定義から次の時刻 t+1 における最適状態確率が導出される

33. “ aab” が出力されたとき , 一番尤もらしい状態系列を Viterbi のアルゴリズムを使って導出してみる s1 s2 s3 0.2 a:0 b:1.0 0.3 a:0.8 b:0.2 0.5 a:1.0 b:0 0.4 a:0.3 b:0.7 0.6 a:0.5 b:0.5

34. 時刻t=0 1.0 0.0 0.0 s1 s2 s3

35. 時刻t=1 1.0 0.0 0.0 s1 s2 s3 0.24 0.5 0.0 a 0.3*0.8 0.5*1.0 0.2*0.0 0.6*0.5 0.4*0.3

36. 時刻t=2 1.0 0.0 0.0 s1 s2 s3 0.24 0.5 0.0 a 0.3*0.8 0.5*1.0 0.2*0.0 0.6*0.5 0.4*0.3 0.057 0.12 0.15 a 0.3*0.8 0.5*1.0 0.4*0.3 0.4*0.3 0.6*0.5

37. 時刻t=3 1.0 0.0 0.0 s1 s2 s3 0.24 0.5 0.0 a 0.3*0.8 0.5*1.0 0.2*0.0 0.6*0.5 0.4*0.3 0.057 0.12 0.15 a 0.3*0.8 0.5*1.0 0.4*0.3 0.4*0.3 0.6*0.5 0.003 0.033 0.036 b 0.3*0.8 0.5*1.0 0.4*0.3 0.4*0.3 0.6*0.5 一番尤もらしい終了状態がわかった！

38. バックトラック 1.0 0.0 0.0 s1 s2 s3 0.24 0.5 0.0 a 0.3*0.8 0.5*1.0 0.2*0.0 0.6*0.5 0.4*0.3 0.057 0.12 0.15 a 0.3*0.8 0.5*1.0 0.4*0.3 0.4*0.3 0.6*0.5 0.003 0.033 0.036 b 0.3*0.8 0.5*1.0 0.4*0.3 0.4*0.3 0.6*0.5 s1=>s1=>s2=>s3 が一番尤もらしい経路

39. Viterbi のアルゴリズムの 形態素解析への利用 “ 東京都”が出現したときに ,” 東京都”が出力される系列中で尤もらしいものを探す . 開始 ->“ 東” -> “ 京都” 開始 ->“ 東京” ->” 都” 開始 ->“ 東京都” 品詞連接確率が遷移確率 単語の出現確率が出力する確率 として Viterbi のアルゴリズムを適用