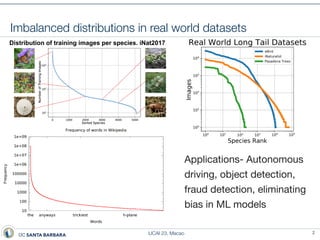
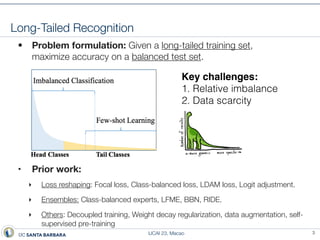
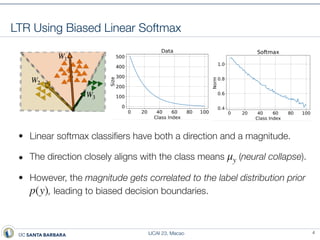
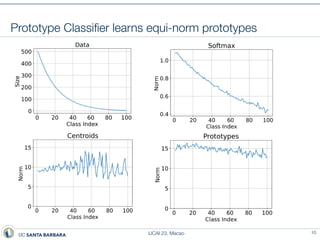
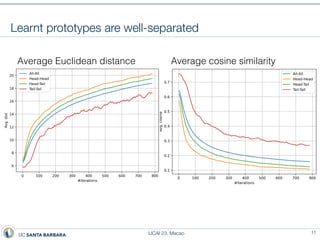
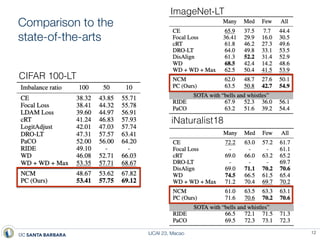
This document presents a method called prototype classifiers for long-tailed recognition (LTR). Prototype classifiers learn a prototype representation for each class and classify examples based on distance to the prototypes. This overcomes biases in linear softmax classifiers caused by imbalanced class distributions. The prototypes are learned to be equi-norm and well-separated. Evaluation on long-tailed benchmarks like CIFAR-100-LT and ImageNet-LT shows prototype classifiers outperform state-of-the-art LTR methods.

1. Learning Prototype Classifiers for Long-Tailed Recognition
Saurabh
Sharma1
1 University of California Santa Barbara, USA
Ning
Yu3
Yongqin
Xian2
Ambuj
Singh1
2 Google, Switzerland
3 Salesforce Research, USA
{saurabhsharma,ambuj}@cs.ucsb.edu
yxian@google.com ning.yu@salesforce.com

2. IJCAI 23, Macao
Imbalanced distributions in real world datasets
2
Distribution of training images per species. iNat2017
Applications- Autonomous
driving, object detection,
fraud detection, eliminating
bias in ML models

3. IJCAI 23, Macao
Long-Tailed Recognition
• Problem formulation: Given a long-tailed training set,
maximize accuracy on a balanced test set.
• Prior work:
‣ Loss reshaping: Focal loss, Class-balanced loss, LDAM loss, Logit adjustment.
‣ Ensembles: Class-balanced experts, LFME, BBN, RIDE.
‣ Others: Decoupled training, Weight decay regularization, data augmentation, self-
supervised pre-training
3
Key challenges:
1. Relative imbalance
2. Data scarcity

4. IJCAI 23, Macao
LTR Using Biased Linear Softmax
• Linear softmax classi
fi
ers have both a direction and a magnitude.
• The direction closely aligns with the class means (neural collapse).
• However, the magnitude gets correlated to the label distribution prior
, leading to biased decision boundaries.
μy
p(y)
4

5. IJCAI 23, Macao
Prototype Classi
fi
ers for LTR
• We propose distance-based classi
fi
cation using learnable
prototypes.
• Prototype classi
fi
ers outperform linear softmax and
nearest-class-mean classi
fi
ers.
• Our theoretical analysis shows that prototype classi
fi
ers
overcome the biased softmax problem.
5

6. IJCAI 23, Macao
Learning Prototype Classi
fi
ers
• We compute pre-softmax logit scores using distances:
where are
fi
xed representations from a baseline model,
and are learnable class prototypes.
• Inference is done using the nearest-prototype rule:
log p(y|g(x)) = −
1
2
d(g(x), cy)
g(x)
cy
6

7. IJCAI 23, Macao
Choice of distance metric
• Euclidean distance:
• Stable gradient updates on prototypes:
• L2 norm of gradient is independent of .
• Only depends on the probability of mis-classi
fi
cation.
• Optimization is robust to outliers that have a high .
d(g(x), cy)
d(g(x), cy)
7

8. IJCAI 23, Macao
Addressing the biased softmax problem
• We show that the prototype classi
fi
er is a linear softmax classi
fi
er,
where:
• Bias term negates the gains from increasing or decreasing
the norm of the weight term.
• The prototype classi
fi
er is robust to imbalanced distributions.
8
weight: cy
bias: −
∥cy∥2
2

9. IJCAI 23, Macao
Channel-dependent temperatures
• As distance scales vary along each channel, we use
channel-dependent temperatures:
• High T Low sensitivity
Low T High sensitivity
• Generalized Mahalanobis distance metric.
⟹
⟹
9

10. IJCAI 23, Macao
Prototype Classi
fi
er learns equi-norm prototypes
10

11. IJCAI 23, Macao
Learnt prototypes are well-separated
11
Average Euclidean distance Average cosine similarity

12. IJCAI 23, Macao 12
CIFAR 100-LT
ImageNet-LT
iNaturalist18
Comparison to the
state-of-the-arts

13. IJCAI 23, Macao
Conclusion
• We present Learnable Prototype Classi
fi
ers for LTR.
• Prototype Classi
fi
ers overcome the intrinsic bias of linear softmax
classi
fi
ers and are robust to imbalanced distributions.
• Euclidean distance based prototype classi
fi
ers are robust to outliers
because of its stable gradient property.
• Learnt prototypes are equi-norm and well-separated.
• For more details, please take a look below:
13
Code
Paper