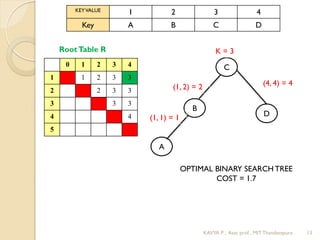
The document discusses the algorithm for constructing an optimal binary search tree. It involves calculating the cost table C and root table R based on the probabilities of keys. The cost C[i,j] is calculated recursively as the minimum of C[i,k-1] + C[k+1,j] + sum of probabilities from i to j. This is done by iterating through all subtrees until the overall minimum cost C[1,n] is found, with the corresponding roots in R. The example calculates the optimal binary search tree for keys A, B, C, D with probabilities 0.1, 0.2, 0.4, 0.3, finding a minimum cost of 1.7.

1. OPTIMAL BINARY
SEARCH TREE
1KAVYA P , Asst. prof. , MIT Thandavapura

2. BINARY SEARCH TREE
2KAVYA P , Asst. prof. , MIT Thandavapura

3. OPTIMAL BINARY SEARCH TREE
Key A B C D
Probability 0.1 0.2 0.4 0.3
C
B
A
D
B
A
D
C
COST = 2.9 COST = 2.1
3KAVYA P , Asst. prof. , MIT Thandavapura

4. Construction of Optimal Binary
Search tree
4KAVYA P , Asst. prof. , MIT Thandavapura

5. 0 1 2 3 4
1 0 0.1
2 0 0.2
3 0 0.4
4 0 0.3
5 0
0 1 2 3 4
1 1
2 2
3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.3
MainTable C RootTable R
C[1,0] = 0
C[2,1] = 0
C[3,2] = 0
C[4, 3] = 0
C[5, 4] = 0
C[1,1] =0.1
C[2,2] = 0.2
C[3,3] = 0.4
C[4,4] = 0.3
R[1,1] = 1
R[2,2] =2
R[3,3] = 3
R[4,4] = 4
C[ i , i-1 ] = 0 C[ i , i ] = p[i] R[ i , i ] = i
5KAVYA P , Asst. prof. , MIT Thandavapura

6.  C [ i , j ] = min i <= k <= j{C [ i , k-1] + C [k+1 , j ] } + 𝑃𝑠
𝑗
𝑠=𝑖
6KAVYA P , Asst. prof. , MIT Thandavapura

7. 0 1 2 3 4
1 0 0.1 0.4
2 0 0.2
3 0 0.4
4 0 0.5
5 0
0 1 2 3 4
1 1 2
2 2
3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.5
MainTable C RootTable R
C[1, 2] = min { C [ 1, 0 ] + C [ 2, 2] , C[1,1] + C[3,2] } + P1 + P2
= min { 0 + 0.2 , 0.1 + 0 } + 0.1 + 0.2
= min { 0.2 , 0.1 } + 0.3
= 0.1 + 0.3
= 0.4 (root = 2)
K = 1 K = 2
7KAVYA P , Asst. prof. , MIT Thandavapura

8. 0 1 2 3 4
1 0 0.1 0.4
2 0 0.2 0.8
3 0 0.4
4 0 0.5
5 0
0 1 2 3 4
1 1 2
2 2 3
3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.3
MainTable C RootTable R
C [ 2, 3] = min { C [ 2, 1 ] + C [ 3 , 3] , C[2,2] + C [ 4 , 3] } + P2 + P3
= min { 0 + 0.4 , 0.2 + 0 } + 0.2 + 0.4
= min {0.4 , 0.2 } +0.6
= 0.2 + 0.6
= 0.8 ( root = 3)
K = 2 K = 3
8KAVYA P , Asst. prof. , MIT Thandavapura

9. 0 1 2 3 4
1 0 0.1 0.4
2 0 0.2 0.8
3 0 0.4 1.0
4 0 0.5
5 0
0 1 2 3 4
1 1 2
2 2 3
3 3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.3
MainTable C RootTable R
C [3, 4] = min { C[ 3, 2] + C[4, 4] , C[3, 3] + C[5,4] } +P3+P4
= min { 0 + 0.3 , 0.4 + 0 } + 0.4 + 0.3
= min { 0.3, 0.4} +0.7
= 0.3+ 0.9
= 1.0 (root = 3)
K = 3 K = 4
9KAVYA P , Asst. prof. , MIT Thandavapura

10. 0 1 2 3 4
1 0 0.1 0.4 1.1
2 0 0.2 0.8
3 0 0.4 1.0
4 0 0.5
5 0
0 1 2 3 4
1 1 2 3
2 2 3
3 3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.3
MainTable C RootTable R
C [ 1, 3 ] = min { C[1,0]+C[2,3] , C[1, 1] + C[3, 3] , C[1, 2] +C[4, 3] } +
P1+ P2 +P3
= min { 0 + 0.8 , 0.1 +0.4, 0.4 + 0} + 0.1 + 0.2 +0.4
= min {0.8 , 0.5 , 0.4 } + 0.7
= 0.4 + 0.7
= 1.1 ( root = 3)
K = 1 K = 2 K = 3
10KAVYA P , Asst. prof. , MIT Thandavapura

11. 0 1 2 3 4
1 0 0.1 0.4 1.1
2 0 0.2 0.8 1.4
3 0 0.4 1.0
4 0 0.5
5 0
0 1 2 3 4
1 1 2 3
2 2 3 3
3 3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.3
MainTable C RootTable R
C[2, 4] = min { C[2,1]+C[3,4] , C[2, 2] + C[4, 4] , C[2, 3] +C[5, 4] } +
P2+ P3 +P4
= min { 0 + 1.0 , 0.2 +0.3, 0.8 + 0} + 0.2 + 0.4 +0.3
= min {1.0 , 0.5 , 0.8 } + 0.9
= 0.5 + 0.93
= 1.4 ( root = 3)
K = 2 K = 3 K = 4
11KAVYA P , Asst. prof. , MIT Thandavapura

12. 0 1 2 3 4
1 0 0.1 0.4 1.1 1.7
2 0 0.2 0.8 1.4
3 0 0.4 1.0
4 0 0.5
5 0
0 1 2 3 4
1 1 2 3 3
2 2 3 3
3 3 3
4 4
5
Key A B C D
Probability 0.1 0.2 0.4 0.3
MainTable C RootTable R
C[1, 4] = min { C[1,0]+C[2,4] , C[1,1] + C[3,4] , C[1, 2] +C[4, 4] , C[1,3]+C[5,4] }
+ P1+ P2 +P3+P4
= min { 0 + 1.4 , 0.1 +1.0, 0.4+0.3 , 1.1+0} + 0.1 + 0.2 + 0.4 + 0.3
= min {1.4, 1.1, 0.7, 1.1} + 1.0
= 0.7 + 1.0
= 1.7 ( root = 3)
K = 1 K = 2 K = 3 K = 4
12KAVYA P , Asst. prof. , MIT Thandavapura

13. 0 1 2 3 4
1 1 2 3 3
2 2 3 3
3 3 3
4 4
5
RootTable R
C
KEYVALUE 1 2 3 4
Key A B C D
K = 3
B
A
D
(1, 2) = 2
(1, 1) = 1
(4, 4) = 4
OPTIMAL BINARY SEARCH TREE
COST = 1.7
13KAVYA P , Asst. prof. , MIT Thandavapura

14. Algorithm Optimal BST
14KAVYA P , Asst. prof. , MIT Thandavapura