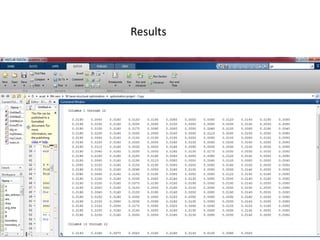
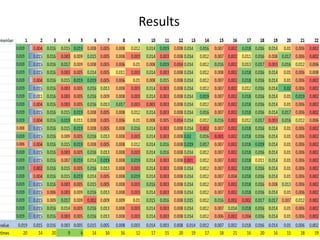
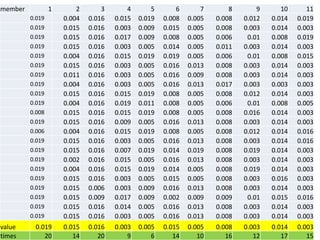
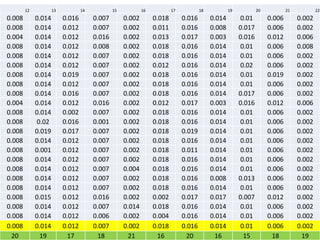
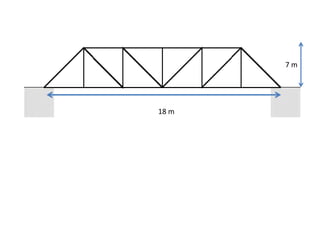
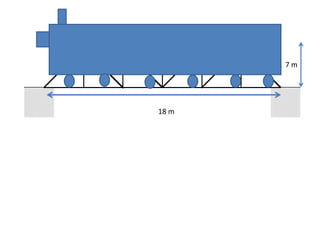
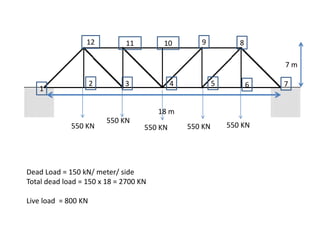
The document describes optimizing the design of a Pratt truss bridge using a genetic algorithm. It presents the objective of minimizing the total cross-sectional area of the truss members subject to constraints on member size and displacement. The genetic algorithm is applied over multiple generations using selection, crossover and mutation to iteratively evolve solutions toward an optimal design. The results show the optimized cross-sectional area in cm^2 for each of the 22 truss members.

1. Pratt Truss Optimization Using
Genetic Algorithm
By :- Harish Kant Soni
Roll No:- 12CE31004

2. Use of Pratt truss
Fig :- Gatton Railway Bridge, Queensland, Australia
Image Source :- https://commons.wikimedia.org/wiki/File:Gatton_Railway_Bridge.JPG

3. Forces in Pratt truss
Image source :-http://www.slideshare.net/sheikhjunaidyawar/trusses-28955458
F

4. 18 m
7 m

5. Loading
Train’s engine has highest weight as compared to other coaches
Indian locomotive class
WAP-5
• Length = 18.16 m
• Weight = 79251.7 kg
Source :- https://en.wikipedia.org/wiki/Indian_locomotive_class_WAP-5

6. 18 m
7 m

7. 18 m
7 m
Dead Load = 150 kN/ meter/ side
Total dead load = 150 x 18 = 2700 KN
Live load = 800 KN
550 KN
550 KN
550 KN 550 KN 550 KN
1
2 3 4 5 6 7
12 11 10 9 8

8. Objective Function:-
min. total Area = min
A(1)+A(2)+A(3)+A(4)+A(5)+A(6)+A(7)+A(8)
+A(9)+A(10)+A(11)+A(12)+A(13)+A(14)+A(15)+
+A(16)+A(17)+A(18)+A(19)+A(20)+A(21)+A(22)
Constraints :-
min. Area = 0.0010 m^2 = 10 cm^2
disp at any node < 50 mm

9. clc; clear all;
% initial cromosome having area in the range 0.002 to 0.02 m^2-
C = 2e-3*[1 2 4 10 3 9 10 7 1 5 1 1 2 4 10 3 9 10 7 1 5 2;
9 3 7 9 4 7 5 2 4 9 1 9 3 7 9 4 7 5 2 4 9 3;
7 3 4 1 1 7 3 2 4 9 8 7 3 4 1 1 7 3 2 4 9 4;
1 5 7 9 4 9 5 2 4 9 6 1 5 7 9 4 9 5 2 4 9 5;
4 10 6 2 2 2 3 2 4 1 9 4 10 6 2 2 2 3 2 4 1 6;
9 3 5 9 5 7 5 1 4 9 1 9 3 5 9 5 7 5 1 4 9 7;
9 9 4 1 4 3 1 2 4 9 8 9 9 4 1 4 3 1 2 4 9 8;
1 3 7 9 1 7 5 5 4 4 1 1 3 7 9 1 7 5 5 4 4 9;
9 8 3 1 2 4 2 2 4 9 6 9 8 3 1 2 4 2 2 4 9 10;
2 3 7 9 3 7 5 9 4 3 1 2 3 7 9 3 7 5 9 4 3 1;
8 7 2 10 4 5 3 10 4 7 4 8 7 2 10 4 5 3 10 4 7 2;
1 2 4 10 3 9 10 7 1 5 1 1 2 4 10 3 9 10 7 1 5 3;
9 3 7 9 4 7 5 2 4 9 1 9 3 7 9 4 7 5 2 4 9 4;
7 3 4 1 1 7 3 2 4 9 8 7 3 4 1 1 7 3 2 4 9 5;
1 5 7 9 4 9 5 2 4 9 6 1 5 7 9 4 9 5 2 4 9 6;
4 10 6 2 2 2 3 2 4 1 9 4 10 6 2 2 2 3 2 4 1 7;
9 3 5 9 5 7 5 1 4 9 1 9 3 5 9 5 7 5 1 4 9 8;
9 9 4 1 4 3 1 2 4 9 8 9 9 4 1 4 3 1 2 4 9 9;
1 3 7 9 1 7 5 5 4 4 1 1 3 7 9 1 7 5 5 4 4 10;
9 8 3 1 2 4 2 2 4 9 6 9 8 3 1 2 4 2 2 4 9 1;
2 3 7 9 3 7 5 9 4 3 1 2 3 7 9 3 7 5 9 4 3 2;
2 3 7 9 3 7 5 9 4 3 1 2 3 7 9 3 7 5 9 4 3 3];

10. F_obj= sum(C,2); % return sum of rows in a column matrix of 22 X 1
%% selection
Fitness = zeros(22,1);
for a = 1:22
Fitness(a) = (1/(1+F_obj(a)));
end
S = sum(Fitness);
Prob_of_cromosome = Fitness/S;
roullet = zeros(22,1);
roullet(1) = Prob_of_cromosome(1);
for a = 2:22;
roullet(a) = roullet(a-1) + Prob_of_cromosome(a); %CDF
end

11. %% new set of cromosome
for a = 1 : 22
r = rand;
if (r <= roullet(1))
new_cromosome_id = 1;
else
for b = 1 : 21
if (r > roullet(b) & r <= roullet(b+1))
new_cromosome_id = b+1;
end
end
end
C(a,:) = C (new_cromosome_id,:);
end

12. %% Cross Over
C_new = C;
for a= 1:22
r_crossover = rand();
if(r_crossover < 0.7)
r_location = 10*round(rand(),1); % generates random number between 0 to 10. It
selects location for crossover
for b = r_location+1 : 22
if (a==22)
C_new(a,b)= C(1,b);
C_new(1,b) = C(22,b);
else
C_new(a,b)= C(a+1,b);
C_new(a+1,b) = C(a,b);
end
end
end
end

13. %% Mutation Probability 0.1
for a=1:22
for b=1:22
if(rand < 0.1)
C_new(a,b)= round(((0.02-0.001)*rand+0.001),3);
end
end
end

14. %% Truss code
coordinate=[0 0 ;3 0 ;6 0;9 0; 12 0; 15 0; 18 0;15 7; 12 7; 9 7; 6 7; 3 7;];
connectivity=[1 2;2 3;3 4;4 5;5 6; 6 7; 7 8;8 9; 9 10;10 11; 11 12;1
12; 2 12;3 12;3 11; 4 11;4 9; 4 10; 5 9; 5 8;6 8; 7 8];
boundary=[1 1 ; 0 0 ; 0 0 ;0 0 ;0 0;0 0; 1 1;0 0; 0 0;0 0;0 0;0 0];
load=[0 0 0 -550e3 0 -550e3 0 -550e3 0 -550e3 0 -550e3 0 0 0 0 0 0
0 0 0 0 0 0];
Elasticity=2.E+11*[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];

15. %% Penalty
abs_unknown_displacement = abs(unknown_displacement);
count = 0;
for k = 1 : 22
for l = 1:20
if(abs_unknown_displacement(k,l)-0.050 > 0)
count = count + 1;
end
C_new(k,:)= (1+0.05*count)*C_new(k,:);
end
end

16. Results

17. Results

18. member 1 2 3 4 5 6 7 8 9 10 11
0.019 0.004 0.016 0.015 0.019 0.008 0.005 0.008 0.012 0.014 0.019
0.019 0.015 0.016 0.003 0.009 0.015 0.005 0.008 0.003 0.014 0.003
0.019 0.015 0.016 0.017 0.009 0.008 0.005 0.006 0.01 0.008 0.019
0.019 0.015 0.016 0.003 0.005 0.014 0.005 0.011 0.003 0.014 0.003
0.019 0.004 0.016 0.015 0.019 0.019 0.005 0.006 0.01 0.008 0.015
0.019 0.015 0.016 0.003 0.005 0.016 0.013 0.008 0.003 0.014 0.003
0.019 0.011 0.016 0.003 0.005 0.016 0.009 0.008 0.003 0.014 0.003
0.019 0.004 0.016 0.003 0.005 0.016 0.013 0.017 0.003 0.003 0.003
0.019 0.015 0.016 0.015 0.019 0.008 0.005 0.008 0.012 0.014 0.003
0.019 0.004 0.016 0.019 0.011 0.008 0.005 0.006 0.01 0.008 0.005
0.008 0.015 0.016 0.015 0.019 0.008 0.005 0.008 0.016 0.014 0.003
0.019 0.015 0.016 0.009 0.005 0.016 0.013 0.008 0.003 0.014 0.003
0.006 0.004 0.016 0.015 0.019 0.008 0.005 0.008 0.012 0.014 0.016
0.019 0.015 0.016 0.003 0.005 0.016 0.013 0.008 0.003 0.014 0.016
0.019 0.015 0.016 0.007 0.019 0.014 0.019 0.008 0.019 0.014 0.003
0.019 0.002 0.016 0.015 0.005 0.016 0.013 0.008 0.003 0.014 0.003
0.019 0.004 0.016 0.015 0.019 0.014 0.005 0.008 0.019 0.014 0.003
0.019 0.015 0.016 0.003 0.005 0.015 0.005 0.008 0.003 0.016 0.003
0.019 0.015 0.006 0.003 0.009 0.016 0.013 0.008 0.003 0.014 0.003
0.019 0.015 0.009 0.017 0.009 0.002 0.009 0.009 0.01 0.015 0.016
0.019 0.015 0.016 0.014 0.005 0.016 0.013 0.008 0.003 0.014 0.003
0.019 0.015 0.016 0.003 0.005 0.016 0.013 0.008 0.003 0.014 0.003
value 0.019 0.015 0.016 0.003 0.005 0.015 0.005 0.008 0.003 0.014 0.003
times 20 14 20 9 6 14 10 16 12 17 15

19. 12 13 14 15 16 17 18 19 20 21 22
0.008 0.014 0.016 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.011 0.016 0.008 0.017 0.006 0.002
0.004 0.014 0.012 0.016 0.002 0.013 0.017 0.003 0.016 0.012 0.006
0.008 0.014 0.012 0.008 0.002 0.018 0.016 0.014 0.01 0.006 0.008
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.012 0.016 0.014 0.02 0.006 0.002
0.008 0.014 0.019 0.007 0.002 0.018 0.016 0.014 0.01 0.019 0.002
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.016 0.007 0.002 0.018 0.016 0.014 0.017 0.006 0.002
0.004 0.014 0.012 0.016 0.002 0.012 0.017 0.003 0.016 0.012 0.006
0.008 0.014 0.002 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.02 0.016 0.001 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.019 0.017 0.007 0.002 0.018 0.019 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.001 0.012 0.007 0.002 0.018 0.011 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.004 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.008 0.013 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.015 0.012 0.016 0.002 0.002 0.017 0.017 0.007 0.012 0.002
0.008 0.014 0.012 0.007 0.014 0.018 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.006 0.002 0.004 0.016 0.014 0.01 0.006 0.002
0.008 0.014 0.012 0.007 0.002 0.018 0.016 0.014 0.01 0.006 0.002
20 19 17 18 21 16 20 16 15 18 19