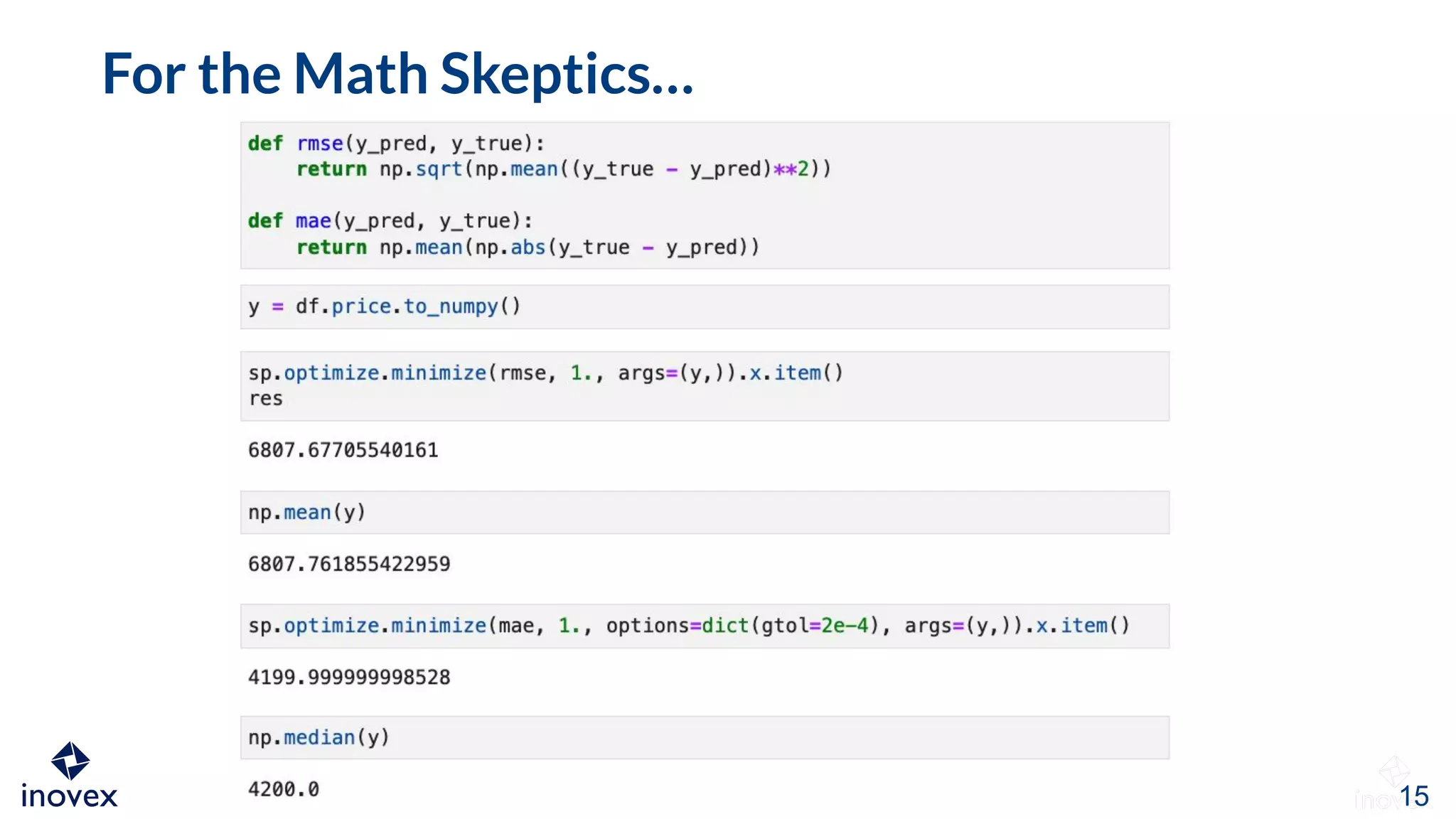
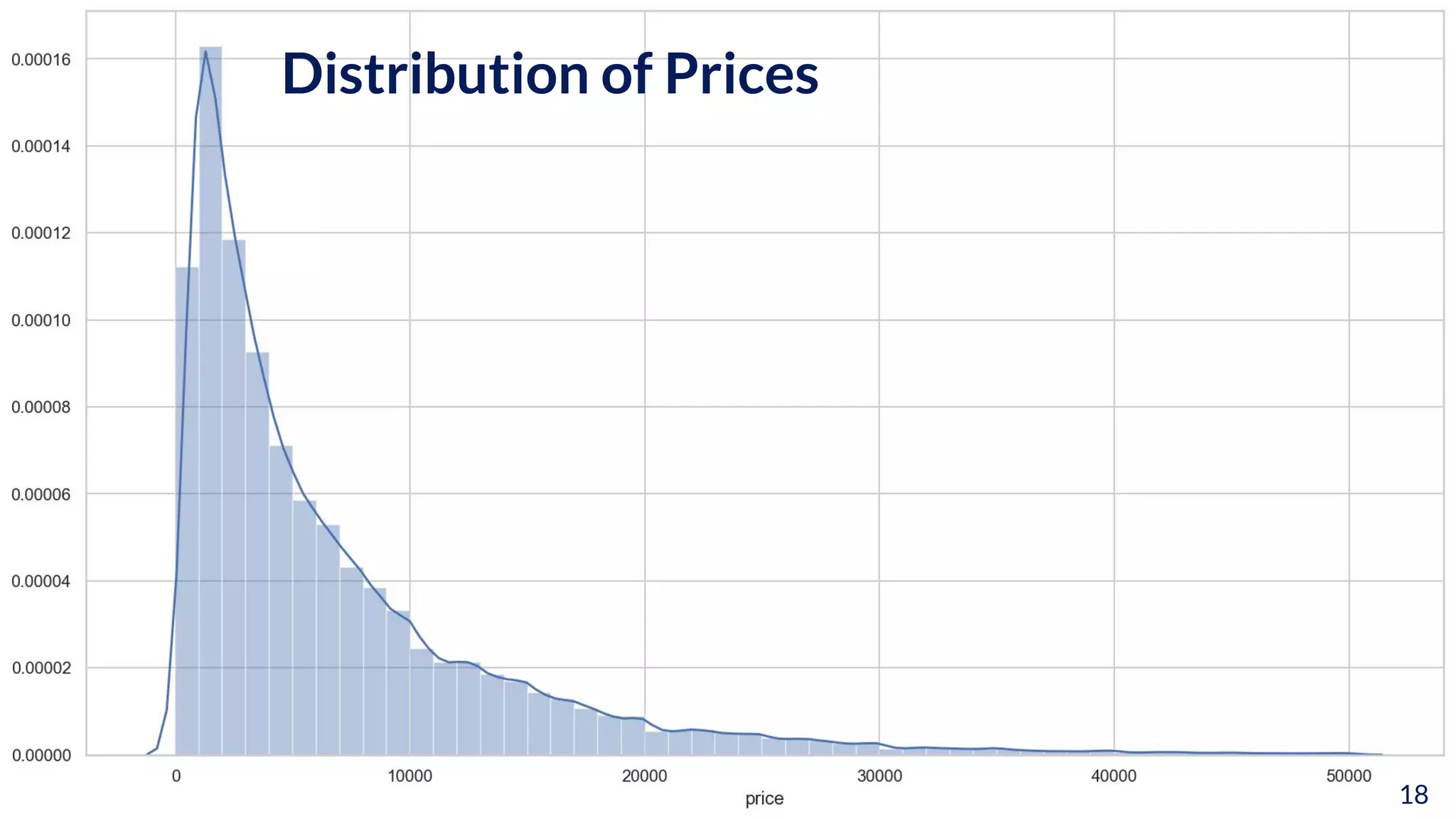
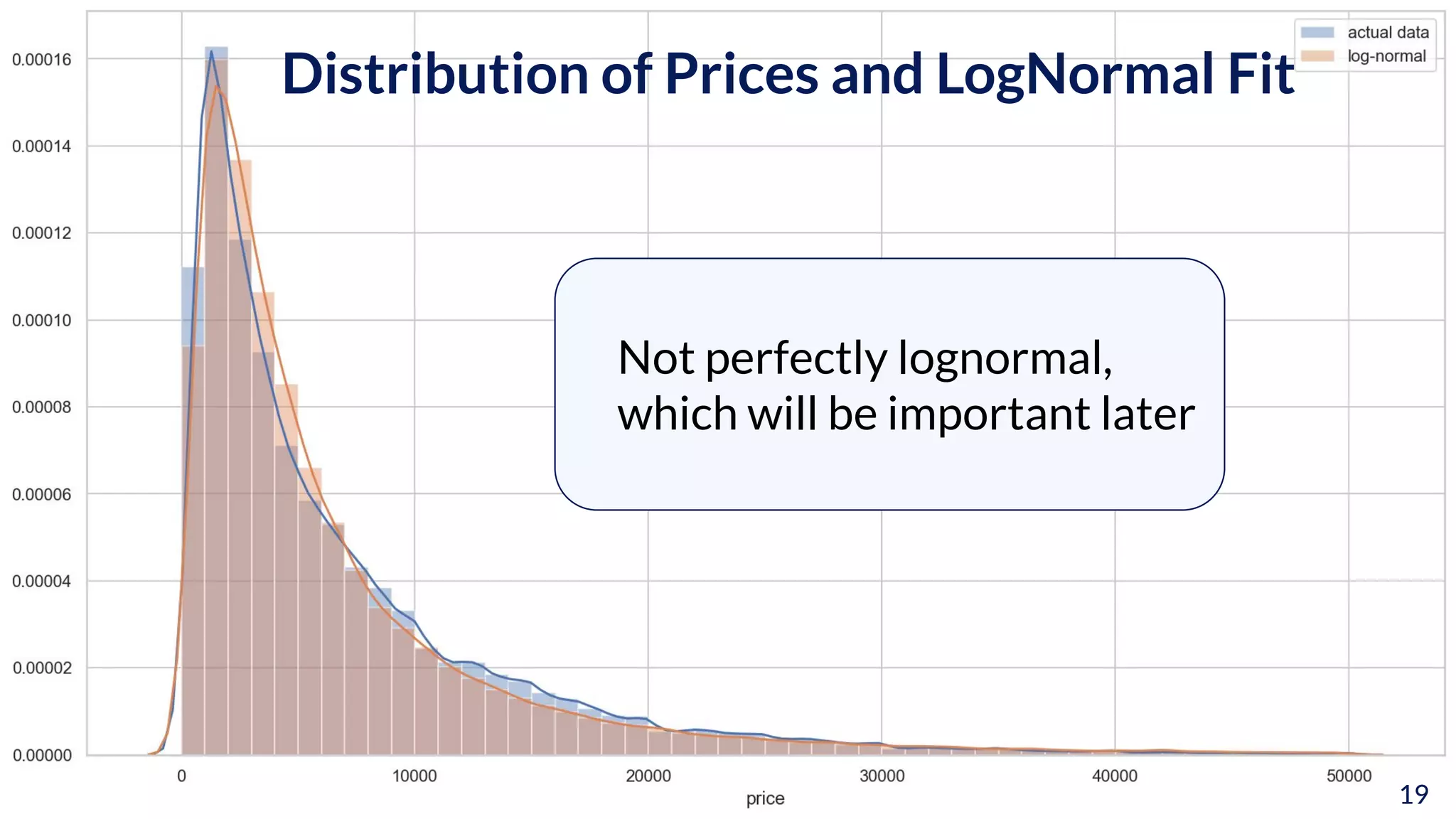
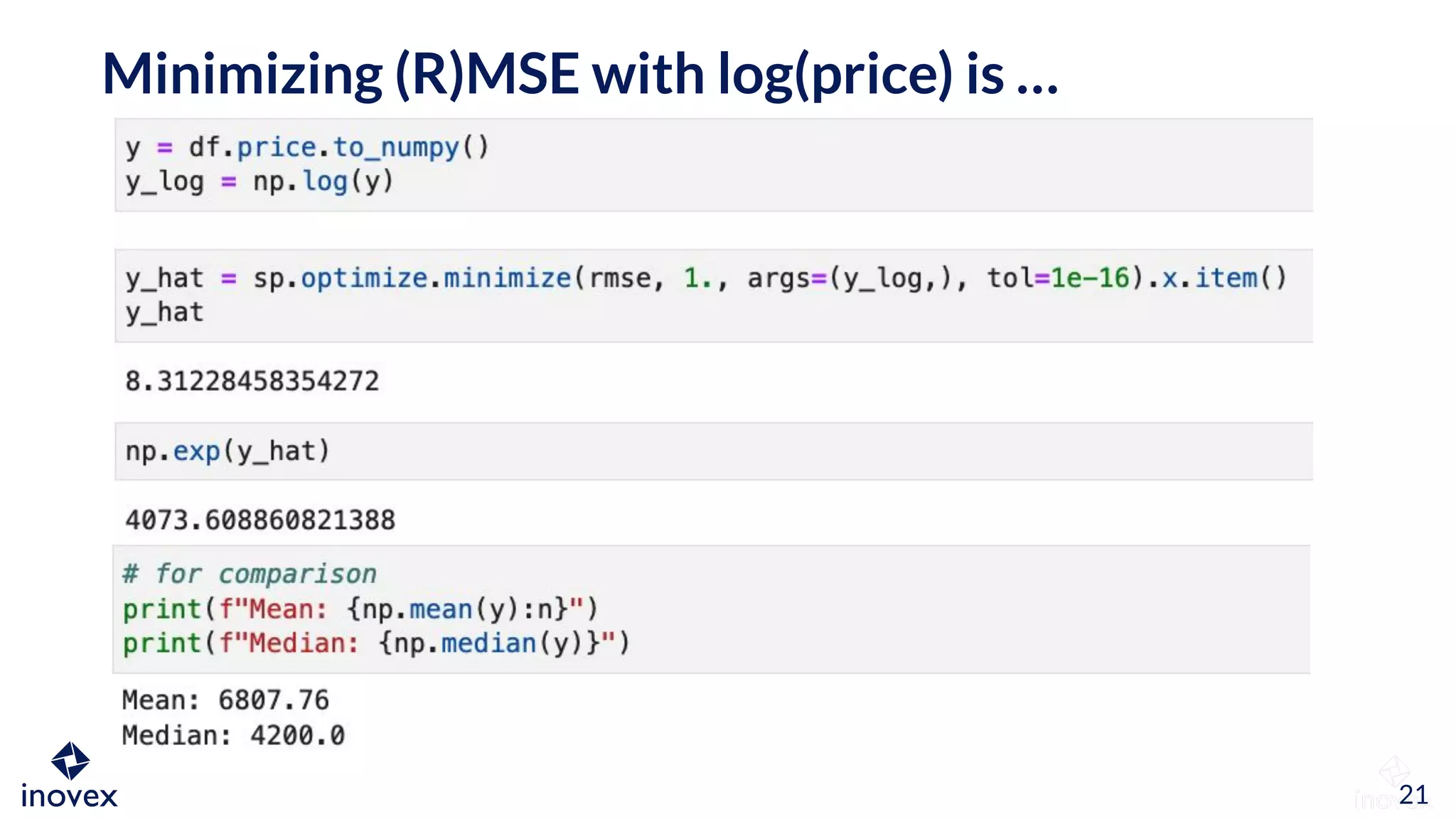
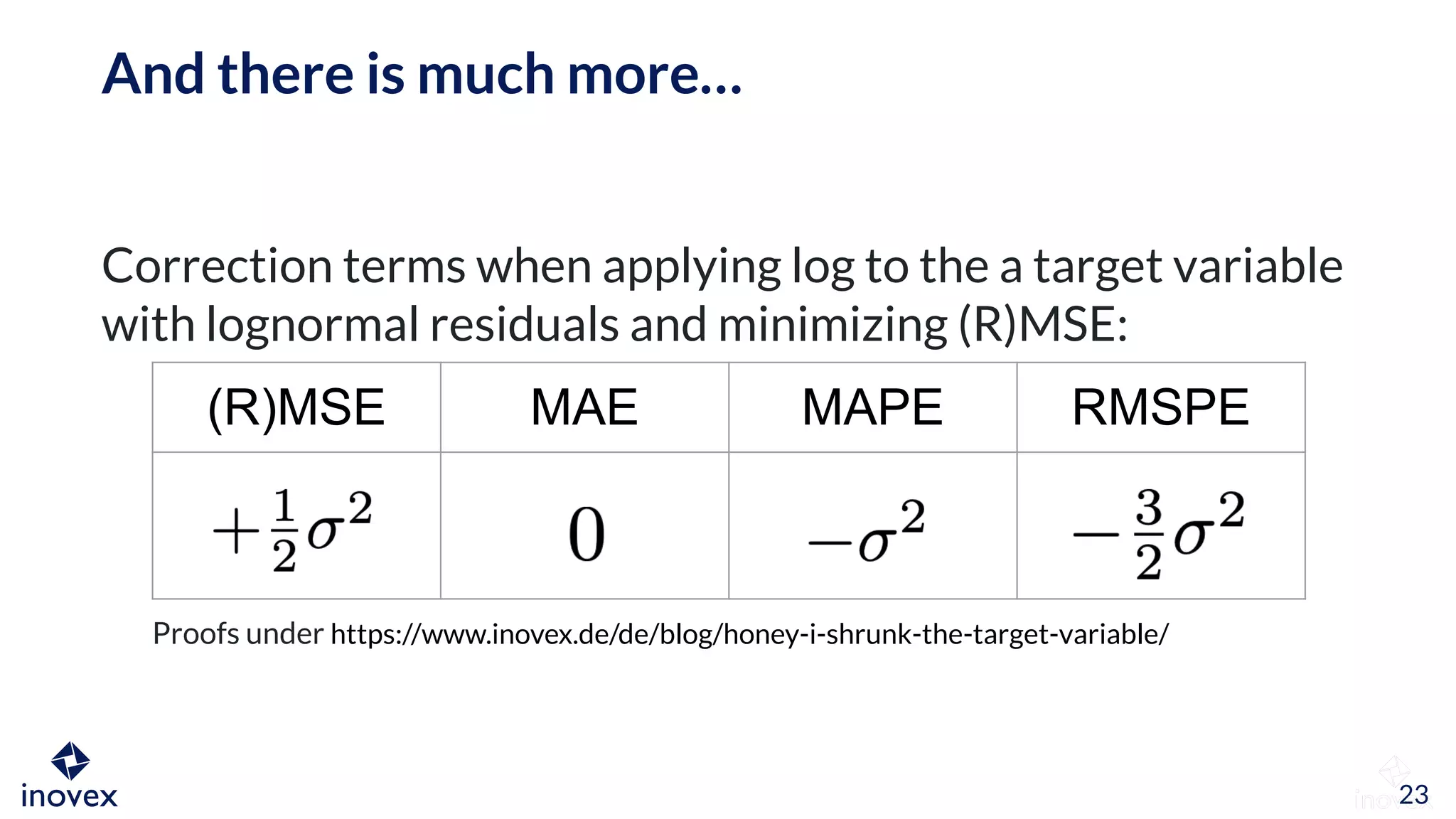
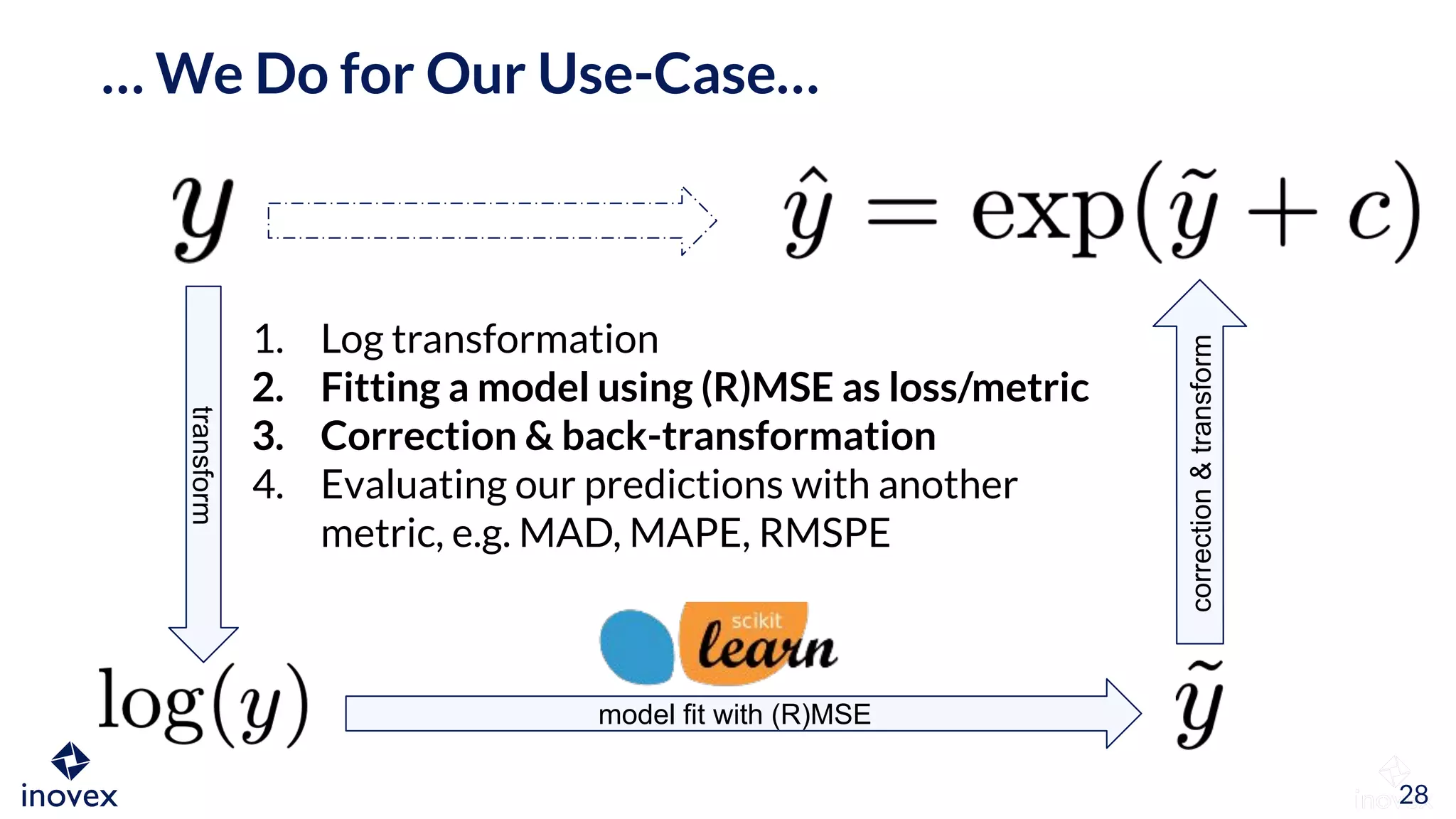
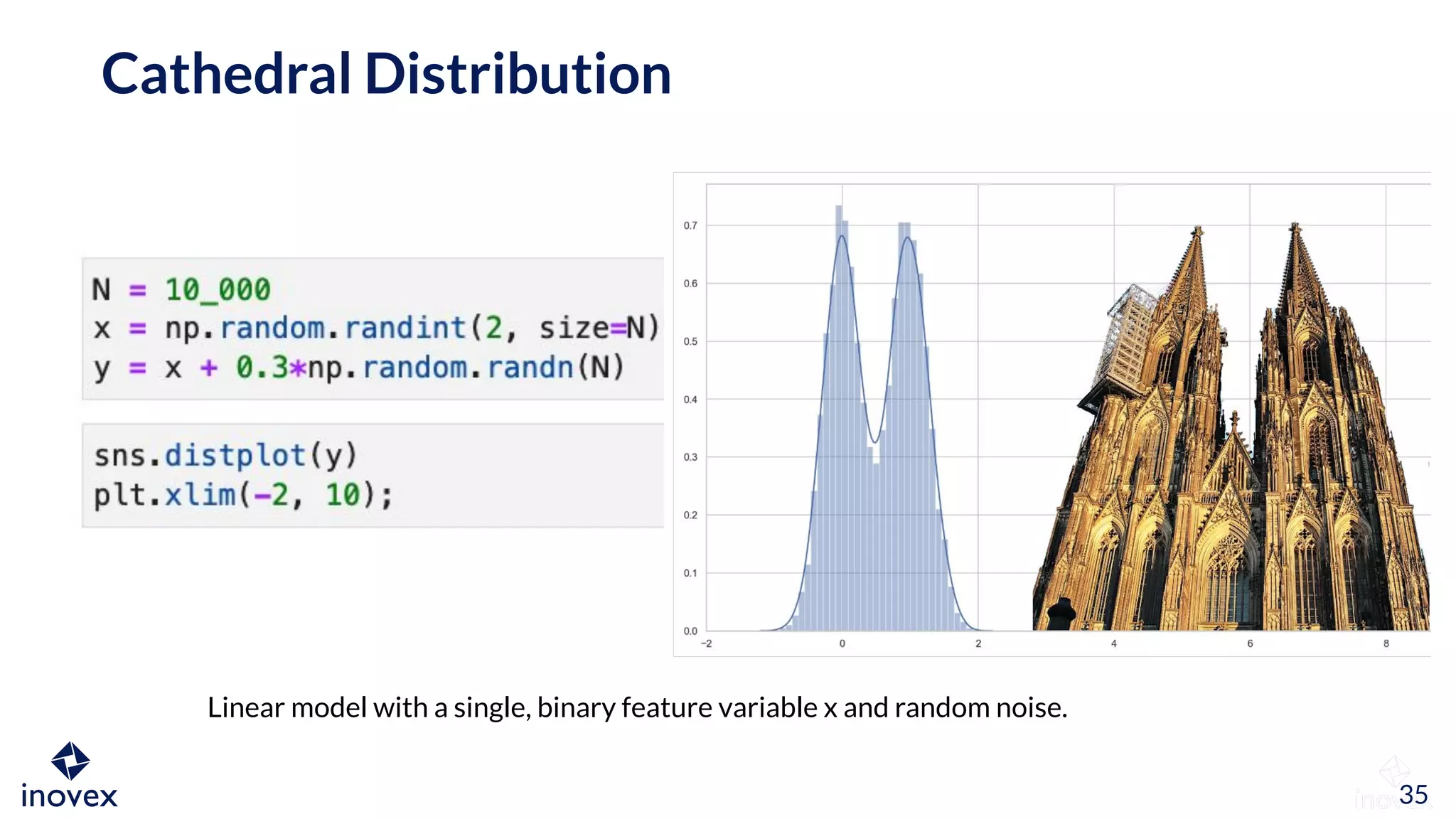
The document discusses the implications of transforming target variables in data science, emphasizing that the choice of metric affects model results. It highlights the advantages of using log transformations to minimize residual error metrics like (r)mse and the importance of correcting results based on the distribution of data. Key insights include that the mean minimizes (r)mse while the median minimizes mae, and the necessity of adjusting metric evaluations when using transformations.

1. Honey, I Shrunk the Target Variable!
Florian Wilhelm
Common pitfalls when transforming the target variable and
how to exploit transformations
Berlin, April 12th 2022

2. Dein
Foto
hier
Mathematical Modelling
dA Data Science to Production & MLOps
Personalisation & RecSys
Uncertainty Quantification & Causality
Python Data Stack
Creator of PyScaffold
@FlorianWilhelm
FlorianWilhelm
FlorianWilhem.info
2
Dr. Florian Wilhelm
Head of Data Science @ inovex

3. inovex is an IT project house
with focus on digital transformation
› Product Discovery · Product Ownership
› Web · UI/UX · Replatforming · Microservices
› Mobile · Apps · Smart Devices · Robotics
› Big Data & Business Intelligence Platforms
› Data Science · Data Products · Search · Deep Learning
› Data Center Automation · DevOps · Cloud · Hosting
› Agile Training · Technology Training · Coaching
Karlsruhe · Pforzheim · Stuttgart · München · Köln · Hamburg
www.inovex.de/en
Using technology to inspire our clients.
And ourselves.

4. Recap about
Metrics
4

5. Choosing the Right Metric
› (R)MSE is most often
used in practice
› Scikit-Learn’s
regressors use mostly
MSE as default
5
In which Use-Cases does (R)MSE make sense?

6. Quadratic Absolute
Little Recap about Metrics
6
Difference
Relation

7. Our Use-Case
7

8. 8
How much should
I sell my car for?
Model fitted on
many sold cars
and their features
could provide a
fair market value

9. Our Use-Case Setting
9
1. take used-cars database from Kaggle with 370k cars having
features: vehicle type, model, registration date, gearbox,
powerPS, model, mileage, fuel type, brand and price
2. built a model to estimate the price based on these features
and treat this as a fair market value
3. decide what’s a good/fair/bad price based on this fair
market value
source-code: https://github.com/FlorianWilhelm/used-cars-log-trans/

10. Question 1:
10
What’s worse? Selling 10 equal cars
with an actual price of 50,000 € and
1. getting the actual price for 9
but only 40,000 € for the last car or
2. getting 49,000 € for every car?
● For (R)MSE option 1 is much worse
● For MAE both options are equally good/bad

11. Question 2:
11
Which one is worse?
Getting 1,000 € less if your
car’s actual value is
1. 100,000 € or
2. 10,000 €?
● For RMSE & MAE this makes no difference
● For RMSPE & MAPE option 2 is much worse

12. Learning 1:
The right metric depends on the
use-case and will affect your results!
12

13. What does minimizing (R)MSE
actually Mean?
13

14. Minimizing MSE
14
is continuous
random variable
Derive and set to 0:
is actually the Mean!
Analog proof
for MAE and
Median

15. For the Math Skeptics…
15

16. Learning 2:
The mean (expected value) minimizes (R)MSE
and the median minimizes MAE.
16

17. Shrinking the Prices with Log
17

18. 18
18
Distribution of Prices

19. 19
19
Distribution of Prices and LogNormal Fit
Not perfectly lognormal,
which will be important later

20. Minimizing (R)MSE with log(price)
20
What we gonna do:
1. Take log(price) as target variable
2. Minimize (R)MSE to find ŷ
3. Transform ŷ back with exp(ŷ)

21. Minimizing (R)MSE with log(price) is …
21

22. … the Median?!?
Mathematically, in case of a
lognormal residual distribution:
› taking the log, minimizing for
RMSE and transforming back
with exp, will lead to the median.
› if we wanted the mean, we need
to correct the transformed result
by adding .
22
On our data (not perfectly lognormal)
https://www.pinterest.de/pin/494973815284951824/
Uploaded by Jittanisa Sukaphatana
a bit higher than the “actual” mean of 6807

23. And there is much more…
Correction terms when applying log to the a target variable
with lognormal residuals and minimizing (R)MSE:
23
(R)MSE MAE MAPE RMSPE
Proofs under https://www.inovex.de/de/blog/honey-i-shrunk-the-target-variable/

24. Learning 3:
Transforming your target might change the
metric you are actually minimizing!
24

25. Transforming the Target Variable
for Fun & Profit
25

26. What To Do If Your Metric Is Not Supported?
26
Imagine you want to optimise for RMSPE, and your data has
a lognormal residual distribution but the ML-library your
are using only supports (R)MSE?

27. One More Time. Instead of doing…
27
model fit with (R)MSE
1. Fitting a model using (R)MSE as loss/metric
2. Evaluating our predictions with another
metric, e.g. MAD, MAPE, RMSPE

28. … We Do for Our Use-Case…
28
transform
model fit with (R)MSE
correction
&
transform
1. Log transformation
2. Fitting a model using (R)MSE as loss/metric
3. Correction & back-transformation
4. Evaluating our predictions with another
metric, e.g. MAD, MAPE, RMSPE

29. Let’s Apply This In Our Use-Case
29
Improvements over raw target when using a log transformation & correction
and evaluating the final prediction under a given metric, e.g. MAPE, …
In case of the Kaggle competition the
transformation was key for winning
negative numbers mean improvement

30. 30

31. Want to know more?
blog.inovex.de
31
https://www.inovex.de/de/blog/honey-i-shrunk-the-target-variable/

32. Thank you!
Florian Wilhelm
Head of Data Science
inovex GmbH
Schanzenstraße 6-20
Kupferhütte 1.13
51063 Köln
florian.wilhelm@inovex.de

33. Linear Models
&
Normal Distribution
33

34. Recap: Linear Model
34
raw features
(non-linear) functions, feature engineering
weights to fit
true latent (unknown) outcome
noise
observations/samples
Normal Distribution

35. Cathedral Distribution
35
Linear model with a single, binary feature variable x and random noise.

36. Appendix Learning:
The residuals of a linear model should be
normally distributed, not the target variable.
36