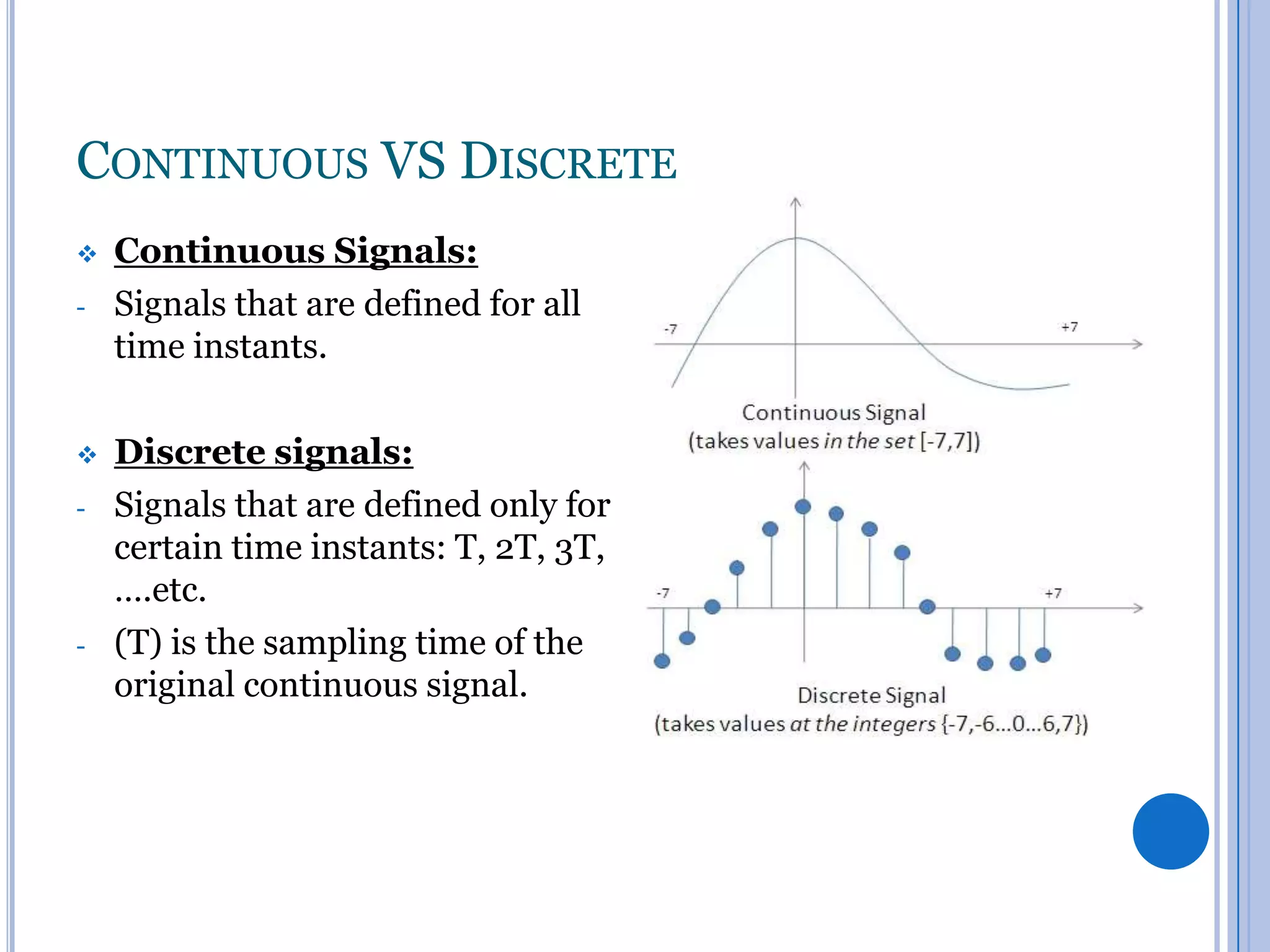
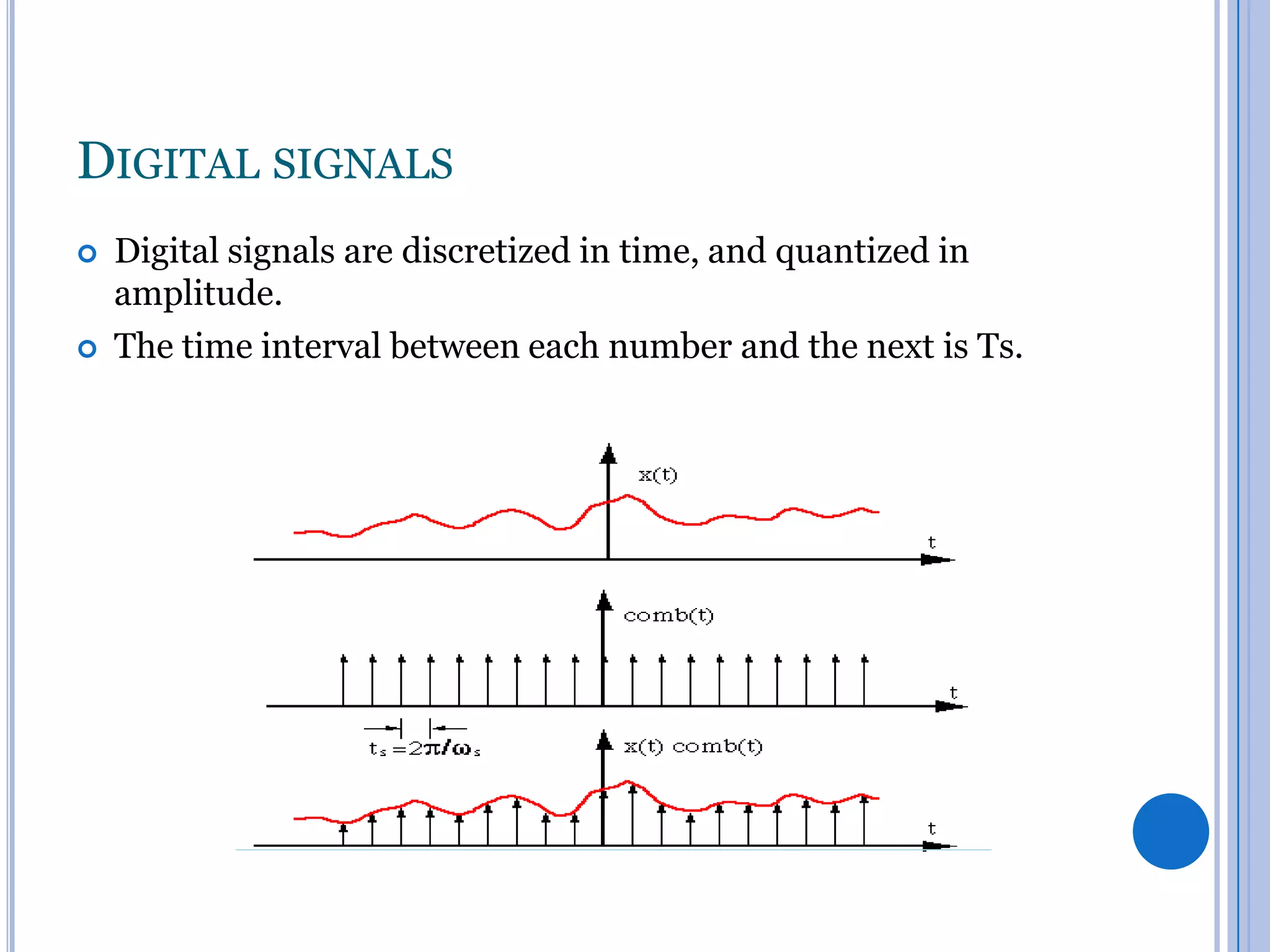
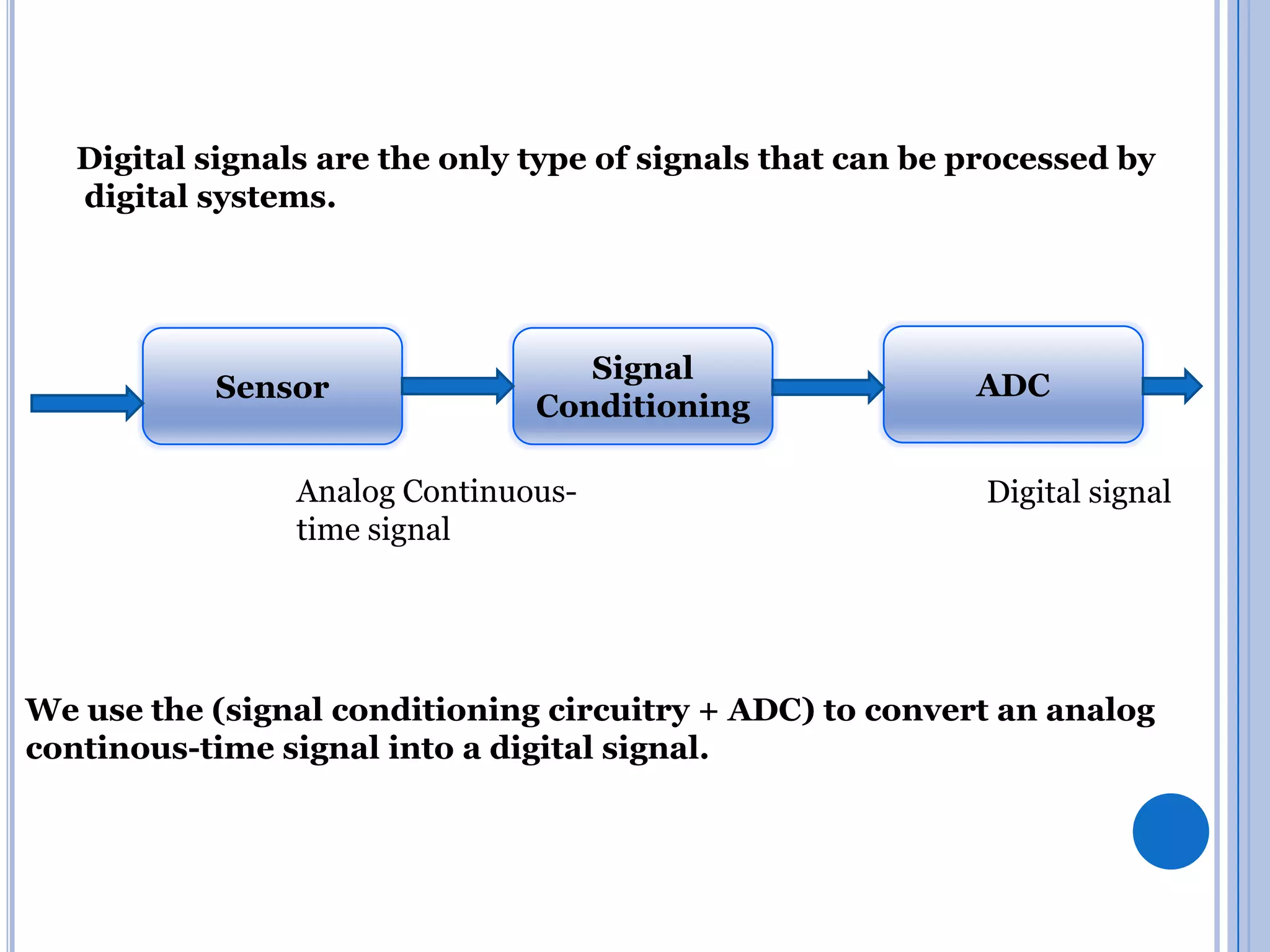
The document discusses analog to digital conversion. It explains that analog signals are continuous while digital signals are discrete in both time and amplitude. It describes how analog signals are converted to digital using sample and hold circuits, quantization, and encoding. The conversion process filters the analog signal, takes samples at regular time intervals, rounds samples to the nearest digital value, and encodes samples into binary format. The document also provides examples of analog to digital converters and discusses considerations like resolution, dynamic range, and signal conditioning.

1. INTERFACING TO THE ANALOG WORLD
Prepared by:
Islam Samir

2. AGENDA
The importance of signals.
 Why do we process signals?
 Continuous VS Discrete.
 Analog signals VS digital signals.
 How to convert an analog signal into digital?
 S/H, Quantization, Encoding.


3. WHAT ARE SIGNALS?

Signals are mathematical functions that represents an
electrical quantity (voltage, current ..etc).

These quantity carries information in one of its
parameters [amplitude, frequency ..etc].

4. WHY DO WE PROCESS SIGNALS?

1.
2.
We’ve to process these signals in an appropriate way to:
Extract the information that they carry.
To get them in a better form (filtering).

5. CONTINUOUS VS DISCRETE

-

-
-
Continuous Signals:
Signals that are defined for all
time instants.
Discrete signals:
Signals that are defined only for
certain time instants: T, 2T, 3T,
….etc.
(T) is the sampling time of the
original continuous signal.

6. ANALOG SIGNALS

For analog signals, the voltage - or current - can take any
value and the system is supposed to respond to this value.

Information is represented by changing the signal’s voltage,
current, frequency, or total charge.
 The amplitude of an analog signal can take any value.

7. THE RULE OF TRANSDUCERS (SENSORS)


Information is converted from some other physical form
(sound, light, temperature ..etc) to an electrical signal
by a transducer.
The processing system (analog or digital) can then take
the right decision based on the electrical quantity that
it monitors, which represents the corresponding
physical quantity.

8. DIGITAL SIGNALS


Digital signals are discretized in time, and quantized in
amplitude.
The time interval between each number and the next is Ts.

9. Digital signals are the only type of signals that can be processed by
digital systems.
Sensor
Signal
Conditioning
Analog Continuoustime signal
ADC
Digital signal
We use the (signal conditioning circuitry + ADC) to convert an analog
continous-time signal into a digital signal.

10. DIGITAL SIGNALS

A digital computer can only deal with binary values, these
values change in a limited range due to the limited word
length.
Ex. For an 8-bit register
28 ) values only.
 It can hold one of 256 (
So, digital signals can take one of certain values only
(Quantized).

11. DIGITAL SIGNALS
-
The hardware that converts an analog signal to digital needs
time to quantize this signal and encode it. Also we need time
for the required processing.
-
We use a (Sample & Hold) circuit that takes samples of the
original continuous signal every time interval (Ts), where:
Ts> hardware delay + processing delay

So, digital signals are discretized in time.
 Digital signals are discretized in both time and
amplitude.

12. ANALOG VS DIGITAL
Analog signals
Digital signals
The signal’s amplitude can take
any value.
The signal’s amplitude is limited to
a certain range of values.
(Quantized)
Can be discrete or continuous in
time.
Always discrete in time.

13. HOW TO CONVERT ANALOG SIGNALS TO
DIGITAL?

14. HOW TO CONVERT ANALOG SIGNALS TO
DIGITAL?
LPF: Low pass filter
S/H: Sample and hold circuit.
X(t): Analog signal to be converted.
X(kTs): Sampled signal.
Xq(kTs): Quantized signal.

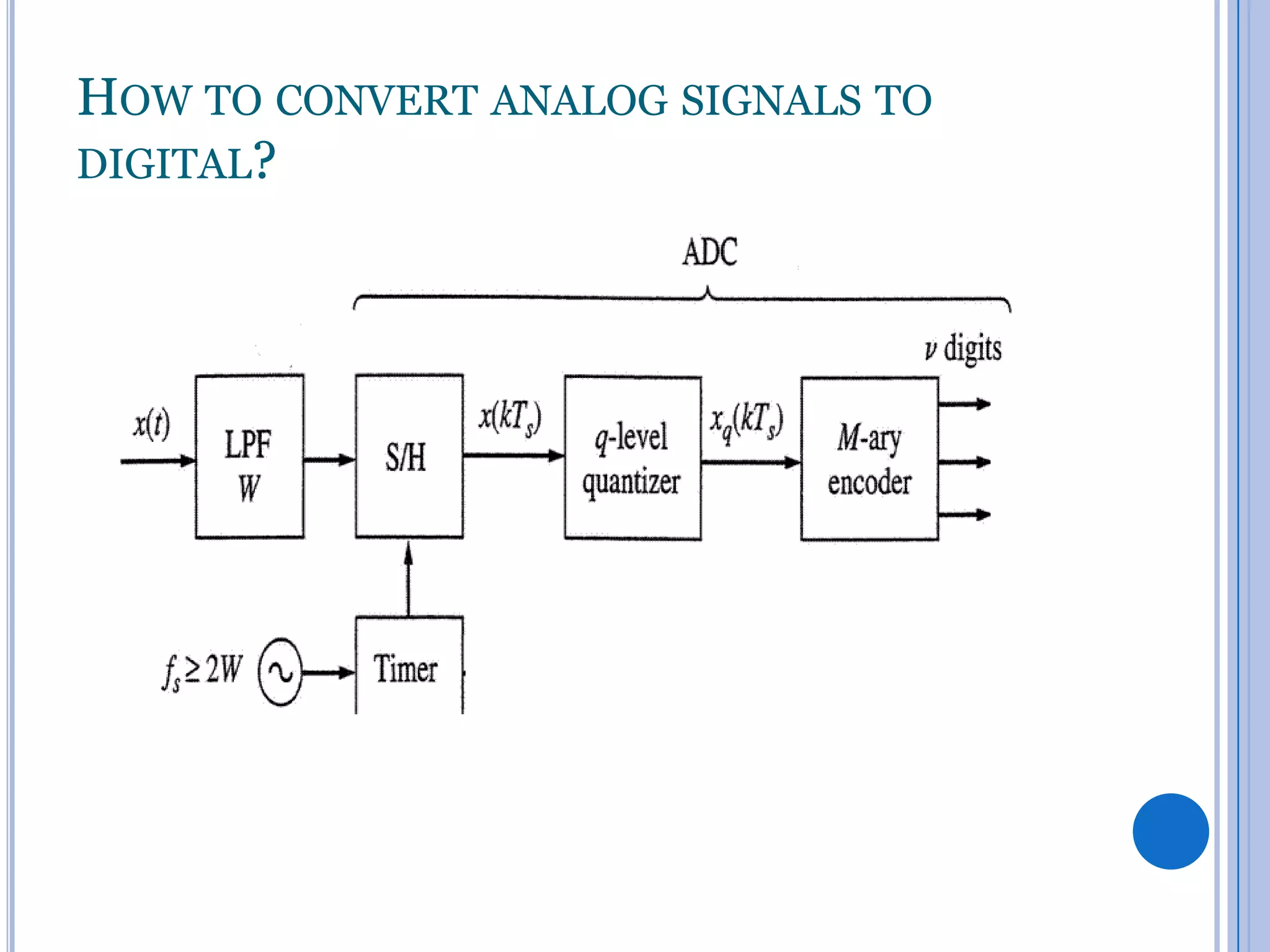
15. HOW TO CONVERT ANALOG SIGNALS TO
DIGITAL?
1.
LPF: The signal is filtered and band limited to 0.5 Fs, in
order to avoid aliasing. (Review sampling theorem)
 Fs≥2Fm
[Nyquist rate]
Fm: the max. signal frequency.
-
1.
2.
If the sampled signal is not band limited, aliasing will occur.
This will result:
The digital signal produced is not representing the original
analog signal.
If we tried to reproduce the analog signal it’ll be distorted.

16. HOW TO CONVERT ANALOG SIGNALS TO
DIGITAL?
1.
a)
b)
(S/H):
To convert the continuous signal to a discrete signal.
This is done for two reasons:
A time is required for the ADC to quantize and encode the
coming sample.
A time is required to do the required processing on this
sample.

17. HOW TO CONVERT ANALOG SIGNALS TO
DIGITAL?
Quantizer:
Due to the limited word length of any digital computer , the
sample’s value must be within a certain range according to
the number of bits used to represent the sample.
Ex. If we used an 8 – bit ADC
The sample can take one of 256 values.
3.
 The quantizer has to approximate every sample to
the nearest level.

18. HOW TO CONVERT ANALOG SIGNALS TO
DIGITAL?
4.
-
Encoder:
After quantization, the quantized sample must be encoded
to the corresponding binary value by an encoder.
Usually, the quantizer and the encoder are implemented by
the same hardware.
The use of quantization introduces an error between the
input signal and the signal at the quantizer output.
quantization error or (e)
-
, where: e = X(t) – Xq(kTs)

19. Example.
Discrete & analog signal
Discrete & quantized signal
(Digital signal)

20. ANALOG-TO-DIGITAL CONVERTER

1.
2.
-
The ADC converts an analog sample into the corresponding
digital value according to:
The (Full-scale) voltage. (called also Vref).
The number of bits.
The conversion can be: unipolar (0  +Vfs)
or bipolar (-Vfs  (+Vfs-1LSB)).
or (Vref-)  (Vref +).

21. ANALOG-TO-DIGITAL CONVERTER

In an A/D converter, Q = 1 LSB.
 Q determines the resolution of the system, that is, the lowest
change in voltage that will produce a code change.
Dynamic range:
-
It’s the minimum number of voltage levels needed to
represent a certain voltage signal, according to the range of
this signal and the required resolution.

22. Ex. 4-bit ADC , Vref=10v (Unipolar)
 note that the analog value represented by the all-ones code is
not full-scale (FS), but (FS – 1 LSB).

23. Transfer function of a 3-bit ADC (Unipolar)
-
There is a range of analog input voltage over which the ADC
will produce a given output code; this range is the
quantization uncertainty and is equal to 1 LSB.

24. Ex. 4-bit ADC (Bipolar)
-
In order to maintain perfect symmetry about midscale, the allzeros code (0000) representing negative full-scale (–FS) is not
normally used in computation.

25. Transfer function of a 3-bit ADC (Bipolar)
-
Most ADC ICs are unipolar. To monitor both positive and
negative voltage values, use a level shifter circuit before the
ADC.

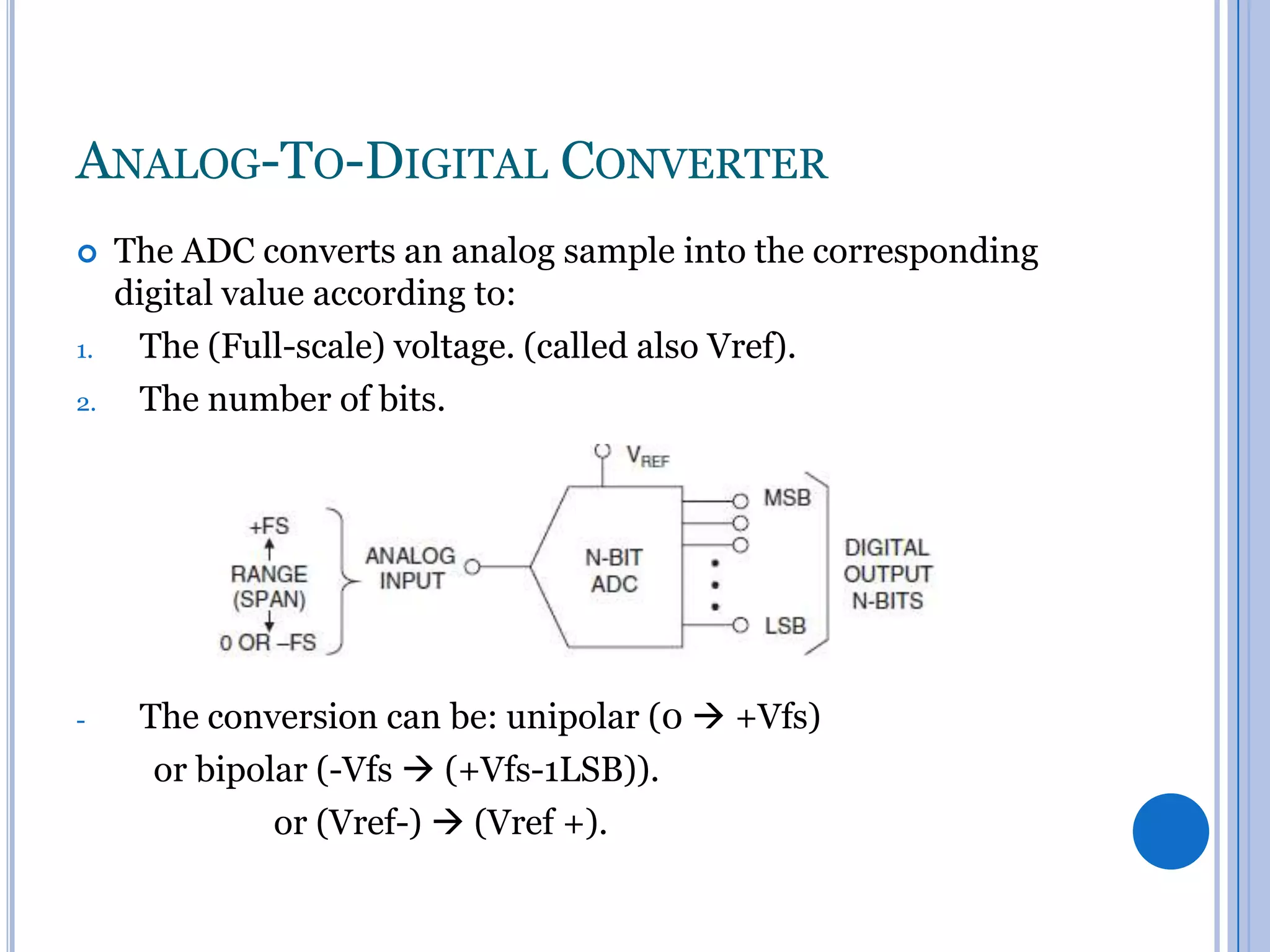
26. SIGNAL CONDITIONING

Typical sensors yield low-amplitude analog signals that need to be
amplified and then digitized by means of an (A/D) converter.

To adapt the analog signal to the range of expected amplitude at the
input of the A/D converter, a signal conditioner is used.
Ex. If the analog signal in the range: [-20mv  20mv]
and the ADC is [0v  5v]
-
The number of values that represent this analog range is small, so
that the quantization noise will be large.
-
If we amplified the signal by (*100) , it’ll be in the range: [-2v  2v]
and the quantization noise is reduced.

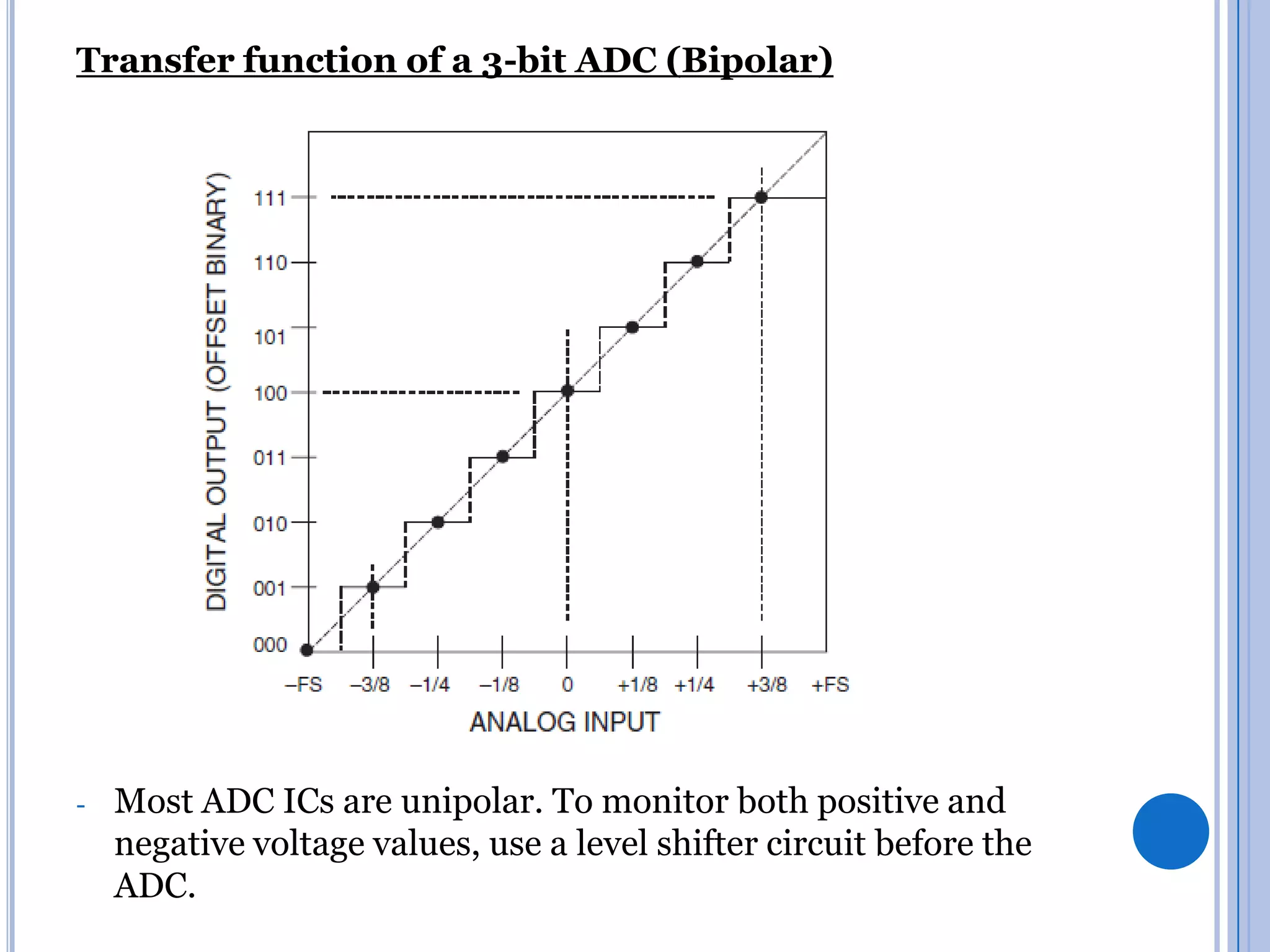
27. SIGNAL CONDITIONING
-
If the analog signal can be +ve or –ve, use a shift up circuit (adder) to
make it in the range [0v  Vref v].

28. Ex.
- We wish to measure a temperature between (–40°C, 60°C) with a
resolution of (0.5°C). How many bits does the A/D converter need?
If we use a sensor with a sensitivity of (1 mV/°C) and an A/D
converter with an input range between (0 V, 5 V), how much gain is
necessary?
1- DR= (60-(-40))/0.5 = 200

We need 200 level at least to represent the output (8-bits).
2- G = 5v/100mv = 50
Or, G= (5v - 0v)/ (60mv – (-40mv)) = 50

We need to shift up the analog voltage 40mv before converting it
by the ADC.

29. THE PIC’S ADC
-
It’s a 10-bit, SAR ADC, with eight multiplexed inputs.
-
It can sample and process signals as fast as 25 kHz or so
accurately.
-
The analog input charges a sample and hold capacitor. The
output of the sample and hold capacitor is the input into the
converter.
-
The A/D module has high and low voltage reference input that
is software selectable to some combination of VDD, VSS, RA2,
or RA3.

30. THE PIC’S ADC

31. THE PIC’S ADC

Acquisition time: After the analog input channel is selected
(changed), you have to wait for this time before the conversion can
be started.

Conversion time: The A/D conversion requires a minimum 12TAD
per 10-bit conversion. (Tad min.=16µs)

How can we get (Tad)?

The four possible options for TAD are: 2Tosc, 8Tosc, 32Tosc,
Internal A/D module RC oscillator.

If you use Tosc to get Tad, ensure that Tad is greater than 16µs.

32. Registers and bits:

A/D Result High Register (ADRESH)

A/D Result Low Register (ADRESL)

The ADRESH:ADRESL registers contain the 10-bit result of the A/D
conversion.

A/D Control Register0 (ADCON0): controls the operation of the A/D
module.

A/D Control Register1 (ADCON1): configures the functions of the
port pins. The port pins can be configured as analog inputs (RA3 can
also be the voltage reference), or as digital I/O.

(GO/DONE~) bit (ADCON0<2>): cleared when the conversion is
done.

ADIF: set when the conversion is done.

33. 
These steps should be followed for doing an A/D
Conversion:
1. Configure the A/D module:
• Configure analog pins/voltage reference and digital I/O (ADCON1)
• Select A/D input channel (ADCON0)
• Select A/D conversion clock (ADCON0)
• Turn on A/D module (ADCON0)
Select the format of the result to be right-justified or left justified.

If you’ll take only
the most significant
8-bits, choose
left justified.

34. 2. Configure A/D interrupt (if desired):
• Clear ADIF bit
• Set ADIE bit
• Set PEIE bit
• Set GIE bit
3. Wait the required acquisition time. (at least 20µs)
4. Start conversion:
• Set GO/DONE bit (ADCON0)
5. Wait for A/D conversion to complete, by either:
• Polling for the GO/DONE bit to be cleared
OR
• Waiting for the A/D interrupt
6. Read A/D result register pair
(ADRESH: ADRESL), clear bit ADIF if required.
7. for the next conversion, go to step 1 or step 2, as required.