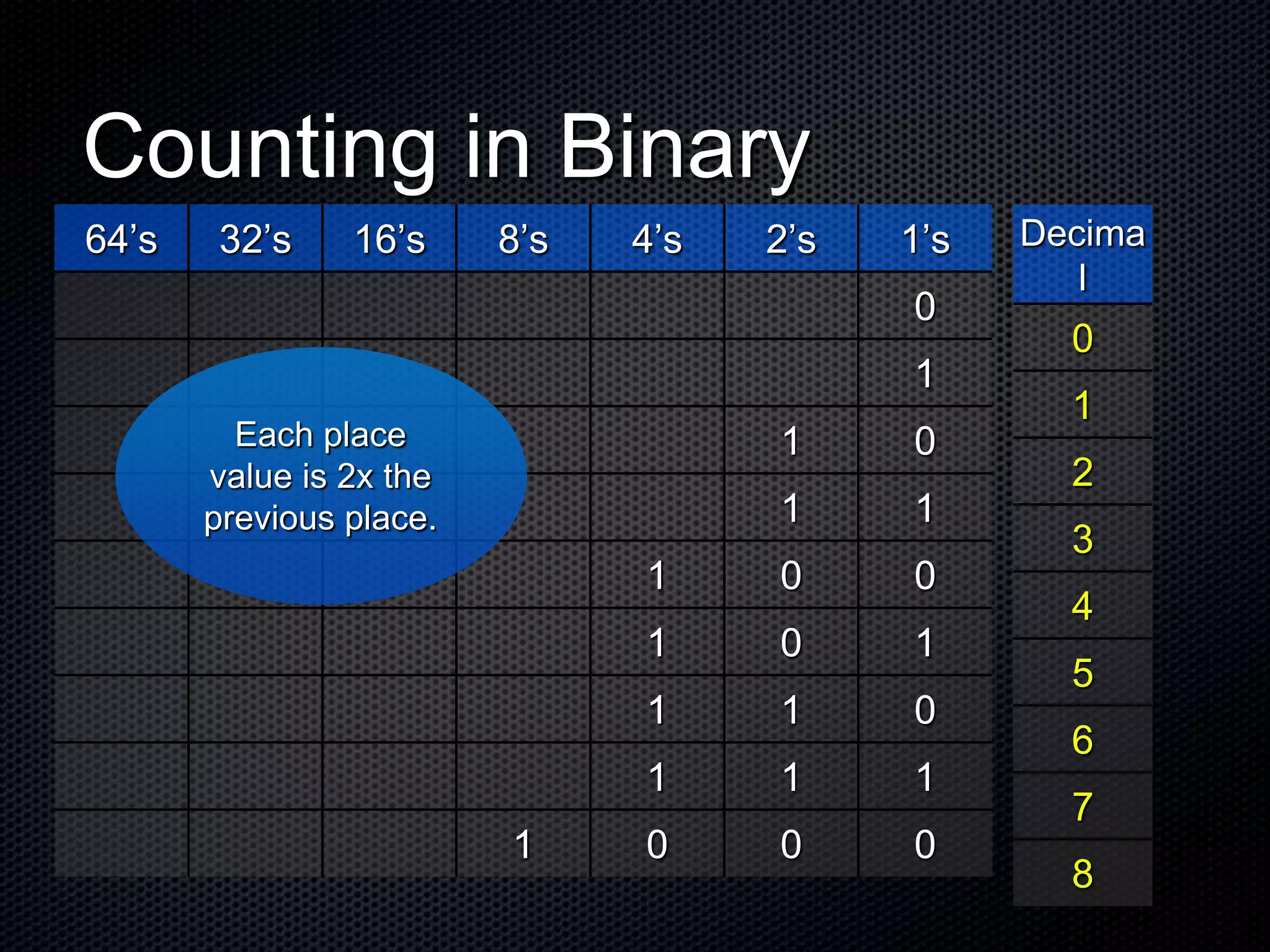
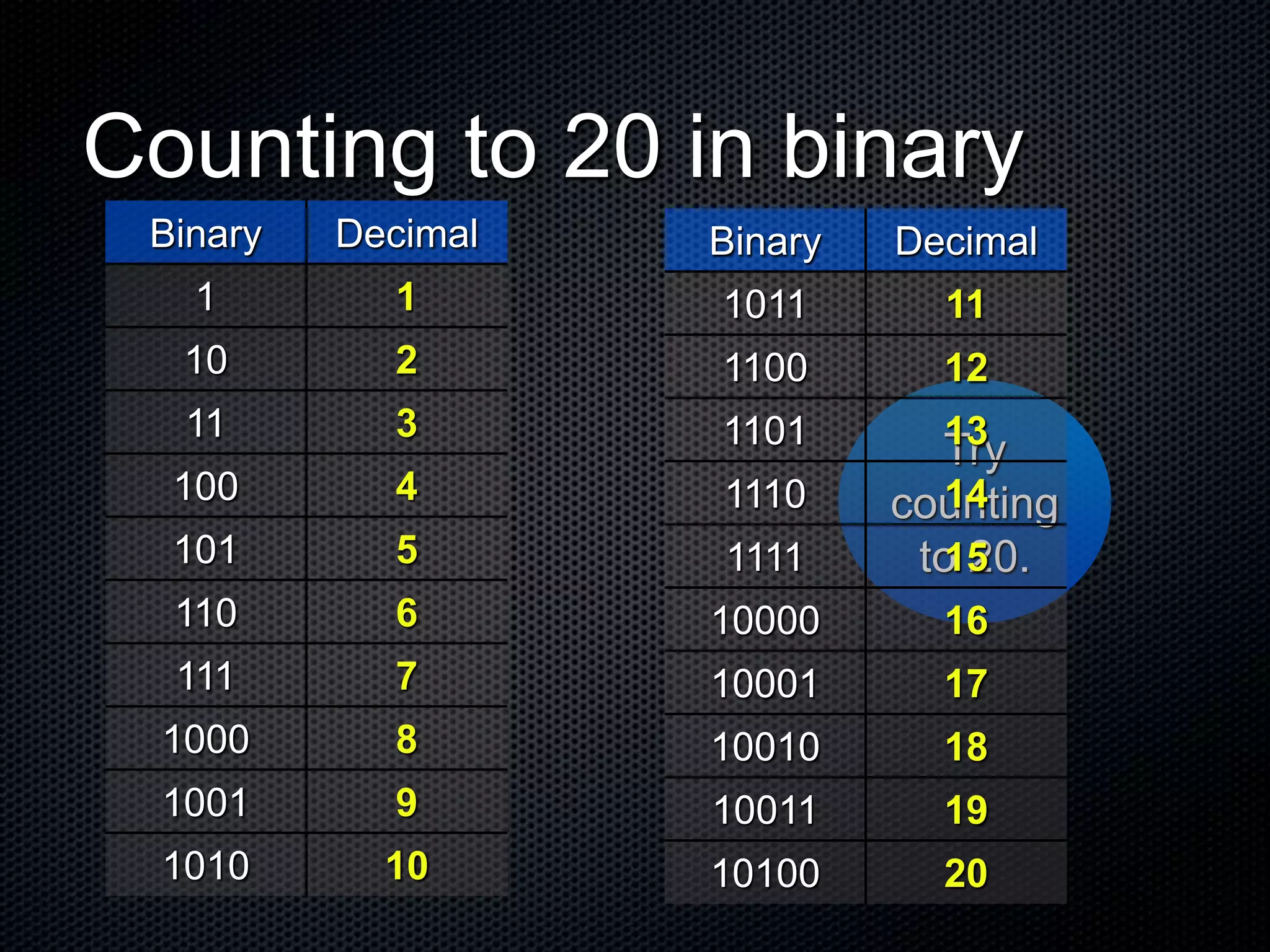
The document explains the concepts of binary code and its fundamental role in computer processing, highlighting the difference between the binary system (base 2) and the decimal system (base 10). It details how data is represented in binary using bits, which are the smallest units, and describes the structure of counting in both systems. Additionally, it includes examples and resources for further understanding of binary code and its applications in programming.

1. Binary Code
The Language of Your Computer

2. Input/Output
Input is whatever is put into a computer.
Input can be data, letters, numbers, symbols, shapes,
sounds, pressure, light beams or whatever material
needs processing.
Output hardware consists of devices that translate
information processed by the computer into a form
humans can understand - print, sound, graphics, or
video, for example.

3. The Binary System
The base of all programs is the binary system, a
number system of two - 1 and 0.
These represent On and Off - the position for an
electrical signal to pass through (or not) a transistor.
All data and program instructions that go into the
computer to be processed and stored, are
represented by these binary numbers.

4. Decimal System
To understand the binary system, we need to review
our Base 10, decimal system.
The prefix “dec-” means 10
Our decimal system is based on 10 numbers
(0,1,2,3,4,5,6,7,8,9)
When counting, using place value, we fill the ones
place and then move to the tens place.

5. For example:
When you count in the
decimal system (base 10)
you fill the one’s place, then
move to the ten’s place.
Only the numbers 0 - 9 are
used.
As each place value is filled
with the numbers, we
continue to the next place
value. Each place value is
10x the previous place.
10’s 1’s
9
1 0
1 1
1 2
1 3
100’s 10’s 1’s
9 9
1 0 0
1 0 1

6. Counting in Binary (Base 2)
The prefix “bi-” means two.
The binary system uses only two numbers - 0 and 1.
We count in the binary system the same as in the
decimal system by filling in the place values and
moving up the place value chart.
If the decimal system, base 10 has place values 10x
the previous place - How do you think the place
values for the binary system are determined?

7. Counting in Binary
0
1
1 0
1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0
Do you see a
pattern?

8. Counting in Binary
64’s 32’s 16’s 8’s 4’s 2’s 1’s
0
1
1 0
1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0
Each place
value is 2x the
previous place.
Decima
l
0
1
2
3
4
5
6
7
8

9. Counting in Binary
64’s 32’s 16’s 8’s 4’s 2’s 1’s
0
1
1 0
1 1
1 0 0
1 0 1
1 1 0
1 1 1
1 0 0 0
110 = 6
one 4, one 2 = 6
1000 = 8
one 8
Decima
l
0
1
2
3
4
5
6
7
8

10. Counting in Binary
64’s 32’s 16’s 8’s 4’s 2’s 1’s
1 0 1 0 0 1
What is this
binary
number?

11. Counting in Binary
64’s 32’s 16’s 8’s 4’s 2’s 1’s
1 0 1 0 0 1
(32) + (0) + (8) + (0) + (0) + 1=
Determine the
place values
and add them
together.
41

12. Try
counting
to 20.
Counting to 20 in binary
Binary Decimal
1 1
10 2
11 3
100 4
101 5
110 6
111 7
1000 8
1001 9
1010 10
Binary Decimal
1011 11
1100 12
1101 13
1110 14
1111 15
10000 16
10001 17
10010 18
10011 19
10100 20

13. Bits and Bytes
Bit - In the binary system, each 0 or 1 is called a bit -
short for binary digit.
Byte - A group of eight bits. The letter “G” is a
representation of 1 byte (eight bits).
There are 256 combinations of bits available 28=256

14. The alphabet in binary
Binary Alphabet
O11OOOO1 a
O11OOO1O b
O11OOO11 c
O11OO1OO d
O11OO1O1 e
O11OO11O f
O11OO111 g
O11O1OOO h
O11O1OO1 i

15. Can you read this?
O11O1OOO_O11O1OO1
Binary code is the base code of computer
language.
Once you understand the patterns and the
rules, you can learn other programming
languages.
Have fun coding!

16. Sources
Adapted from, Using Information Technology,
Williams/Sawyer

17. Additional Teaching Links
Text to Binary and Back Again
http://www.roubaixinteractive.com/PlayGround/Binary_Conversion/Binary_To_Text.a
sp
The Alphabet in Binary
http://www.tekmom.com/buzzwords/binaryalphabet.html
Cisco Binary Game
http://forums.cisco.com/CertCom/game/binary_game_page.htm
http://www.networkclue.com/hardware/computer/binary.aspx
http://en.wikipedia.org/wiki/Binary_numeral_system