AS LEVEL Trigonometry (CIE) EXPLAINED WITH EXAMPLE AND DIAGRAMS

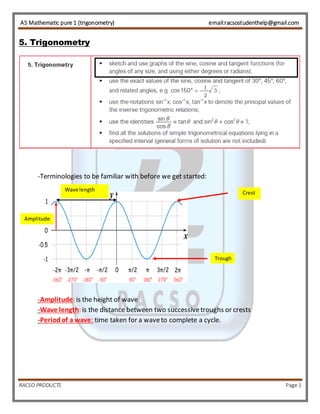
AS Mathematic pure 1 (trigonometry) email:racsostudenthelp@gmail.com
5. Trigonometry
-Terminologies to be familiar with before we get started:
Amplitude
Wave length
Trough
Crest
-Amplitude: is the height of wave
-Wave length: is the distance between two successive troughs or crests
-Period of a wave: time taken for a wave to complete a cycle.
RACSO PRODUCTS Page 1

 Sine graph
 Cosine graph
A cosine has a period of 180o or π
radians also. Meaning a new wave
starts after every 180o or π radians.
Radians
Meanin
g a new
wave
starts
after
every
180o or
π
radians.
n
A sine graph has a period of 180o
or π radians. Meaning a new
wave starts after every 180o or π
radians.
Radians
Degrees
Degrees
Y

 Tangent graph
-What does it mean by a wave completing one cycle?
Look at the example below.
Figure ( i)
A tangent graph has a
period of 90o or π/2
radians. Meaning a new
tangent graph starts after
90o or π/2 every
Radians
Degrees
-An easy way to remember, look at the part of
wave circled, they look like 2 half circles (semi-circles).
2 semi-circles make one complete
circle.
2 half waves= Make a waves one complete cycle

Figure (ii)
-The graph on the left, the wave complete one
cycle at 2π radians or 360o.
Look at this wave, one complete cycle ends at
π radians or 180o. In other words this wave
complete one cycle earlier.
When a wave finishes one complete cycle
earlier that the other we say it has a higher
frequency.
That means wave on figure (ii) is faster
than the one on figure (i).
It is not very necessary for you to
know this for you example, it only
make your understanding better.

-Transformation of a wave:
A general equation of a wave is y = a sin bx ± d.
From the general equation y = a sin bx ± d. on this page we changed “b”
y = sin bx
(a) Y = sin x (b)
Look at what happens to the graph when b=2.
And therefore eqn; y= sin 2x, and when b=3,
y= sin 3x. As b increases period decreases and
vice versa
( c ) Y = six 2x
Y=sin
1
2
Y = sin x/2 Or
푥
Look at the difference between figure (a)
and (b) on changing “b”. figure (a) has b=1
figure (b) has b= ½ .
In figure (b), b is decreased and the fore
period increased.
(D) Y = sin 3x
If you want to know where the graph complete one cycle, take 360/b or 2π/b. take an example of figure (c). b=2.
Therefore 2π/2 = π. That means one complete cycle ends at π radians.

y = a sin x We are now changing “a”
Y= 2 sin x
Y= ½ sin x
Y= sin x
Same as Y =1sin x
Noticed anything? When a= 2 graph
stretched vertical, and its amplitude
becomes 2, when a=1, amplitude is 1 so on.

‘’d ‘’ will be changed, and see the resulting changes on the graph.
From equation y = sin x ± d
Y= sin x + 1
Y= sin x -1
Y= sin x, the same as Y= sin x + 0

-From the equation y = a sin bx ± d all the variables a, b and d will be changed.
Example 1: write down the equation of the graph below.
-The equation is y = a sin bx ± d,
-Let me find out what d is, I look at where by graph intersects the y-axis. It is +1, hence d= +1/2
- We now know what d is so we know where the horizontal axis is . look at diagram below
2.5

0.5
2.5- 0.5= 2.0, hence a=2.0
The amplitude is 2.0
-b is the period. We learnt a formula that period= 2π / b. We know the period is π radians
(because the graph finishes one complete cycle at π radians.)
So b= 2 π /period = 2 π /π = 2.therefore b= 2.
Y=2sin 2x + 1/2
In the case where a= -ve number, look the difference.
Y= - sin x
Y= sin x

When “a” is negative start drawing downwards for sine, if “a” is positive start by heading
upwards.
Amplitude (strengths graph
vertical)
Period: it determines where graph finishes a complete
cycle.
y = a sin b x ± d
For cosine graphs, it is the same idea with sine,
It shifts the graph, vertically.

Y= cos x
Y= cos x + 1
Y= cos 2x

-How to determine the equation of a cosine graph.
-General formula is y = a cos bx + d.
Y = cos 2x +1
First determine the highest and lowest
points on the graph.
Amplitude= (max. – min)/2.
a = (1.5 – 0.5)/ 2 = 0.5
d = max – min.
d= 1.5 – 0.5 = 1.0

If a= -ve.
Max. = 1.5
Min = 0.5
Period = π. Therefore b=2π / period =
2. So b= 2.
Equation; y = ½ cos 2x + 1
-If you flip the graph y=cos x upside down it becomes y= - cos x.
y = cos x y = - cos x
For
Tangent
Y = tan x
Period of tangents is 180o or π radians.
So for tangents b= π /period.
Y = - tan x

Y = tan 2x

HOW TO USE THE EXACT VALUES OF SINE, COSINE AND TANGENT
THIS SECTION IS VERY IMPORTANT FOR YOUR EXAMS!
A unit circle: is a circle with a radius of one.
-Before starting: try the following questions on your scientific calculator and compare your answers

i) Sin 45 = √ퟑ/ퟐ or 0.577 ii) cos 45 = √ퟐ/ퟐ or 0.701
iii) Sin 135 = √ퟑ/ퟐ or 0.577 IV) cos 135 = −√ퟐ/ퟐ or -0.701
v) Sin 225 = −√ퟑ/ퟐ or - 0.577 VI) cos 225 = −√ퟐ/ퟐ or -0.701
vii) Sin 315 = −√ퟑ/ퟐ or -0.577 viii) cos 315 = √ퟐ/ퟐ or 0.701
i) Tan 45 = ퟏ
ii) Tan 135 = - ퟏ
iii) Tan 225 = ퟏ
iv) Tan 315 = - ퟏ
They are all the same
numbers, the
difference is the sign,
how to determine
where to put what
sign?

Easier way to
remember
Second quadrant
Only sine is positve
(180 – θ)
Third quadrant
Only tangent is
positive
(180 + θ)
This is a unit circle
For the diagram on the previous page,
First quadrant
All positive
A – all
S - Students
T – Take
C - Coffee
- ANGLE AS θ
Forth quadrant
Only cosine is
positive
360 – θ
 All (Sine or cosine or tangent) of any angle in the 1st quadrant is a +ve.
 Sine of any angle in 2nd quadrant is +ve , but tangent and cosine are –ve.
 Tangent of any angle in the 3rd quadrant is positive, but sine and cosine are –ve.
 Cosine of any angle in the 4th quadrant is positive, but sine and tangent are –ve.
- Do your know what a reference angle is? It is the acute version of a certain angle.
Example; 60o is the reference angle of 120o, 240o and 300o.
To determine what the reference angle is ask yourself the following;
1. In what quadrant is the angle given?
2. What is the formula for that specific quadrant?
3. Use the formula to obtain the answer.

Example: find the reference angle of 120o .
θ= reference angle
1. 120o is in the second quadrant.
2. Formula second quadrant is (180 – θ), , 180 – θ = 120o
3. Solve for θ.
4. On solving final answer, θ = 60o
Note: Reference angle should always be 0o < θ< 90o (always from the 1st quadrant)
-You can try for 240 and 300, you should get 60o as the reference angle.

Remember the special angles?
Questions:
Means answers shouldn’t be a decimal (most decimals are approximations)
Find the exact value of the following angles.
i) Sin 60.
ii) Cos 240
iii) Tan 120
Whenever you are asked to find the exact value of
an angle, that angle should be a special angles. If
not specified about the answer you can give it in
any form.
Before answering this kind of question ask yourself the following.
1. In which quadrant is the angle given?
2. Is the value -ve or +ve in that specific quadrant?
A – all
S - Students
T – Take
C - Coffee
3. What is the reference angle of the given angle?
4. Go to the table with special angles to get the value.
5. Don’t forget the correct sign on your final answer
depending on step 2
You are required
to know the
table for your
exams.

I will solve the above questions following the steps on previous page.
i) Sin 60.
1. 60o is in the first quadrant,
2. Sine is positive in the first quadrant hence final answer should be positve.
3. The reference angle is the same 60o,
4. from the table, sin 60 = √3/2.
5. The answer is √3/2.
ii) Cos 240.
1. 240o is in the 2rd quadrant.
2. Cosine is –ve in the 3rd quadrant, hence final answer is negative.
3. Reference angle is ( 180 + θ) = 240, θ =60.
4. On the table cos60 = ½
5. Remember the –ve in step 2 hence answer is -1/2
iii) Give part (iii) a try. And you are not expected to write down step by step, this for you to understand.

HOW TO FIND THE INVERSE OF A TRIGONOMETRIC RELATION.
1. How to find inverse of trigonometric relation.
1. What is inverse mean?
Example: it is easy to find what sin 30 is on a calculator.
Sin 30= 0.5
-What if the question is sin x = 0.5, How do u find x?
-At this point you have to find the sine inverse of 0.5, to get the value of x.
-In this case you would have to find sin-1 0.5 to get x.
Sine inverse

-This is the section to master, every year a question comes from this section!
Sin θ /cos θ ≡ tan θ
From the right-angled triangle above;
Sin θ
Cos θ
Note
sin2θ = (sin θ) 2
cos2θ = (cos θ) 2
tan2 θ = (tan θ)2
= a/h ÷ b/ h = a / b
But; Tan θ =
a
b
Therefore,
Tan θ =
Sin θ
Cos θ

Sin θ =opposite / hypotenuse = a / h
Cos θ =adjacent /hypotenuse = b/ h
Tan θ = opposite / adjacent = a / b
- You are NOT expected to prove the equivalence in your exams!
sin2θ + cos2θ ≡ 1
From the right-angled triangle above;
Sin θ =opposite / hypotenuse = a / h
Cos θ =adjacent /hypotenuse = b/ h
Tan θ = opposite / adjacent = a / b
By Pythagoras theorem
a2 + b2= h2 (from the triangle above)
sin 2 θ + cos2 θ = (a / h)2 + (b/ h)2 = (a2 + b2)/ h2 = h2/ h2 = 1.
Therefore; sin2θ + cos2θ ≡ 1
sin2θ = (sin θ) 2
cos2θ = (cos θ) 2
tan2 θ = (tan θ)2
You are not expected to prove this equivalence either, just remember it!
There are different ways you can express identities.
Note
It is all about getting creative with the trigonometric identities, you can always express them in any form

sin cos2θ = 1- sin2θ 2θ = 1 - cos2θ
sin2θ + cos2θ ≡ 1
Squaring both sides;
Sin2 θ /cos2 θ ≡ tan2 θ
Sin θ /cos θ ≡ tan θ
cos2θ = (1 – sinθ)( 1 + sinθ)
If sin2θ Is divide throughout:
1 + 1 / tan2 θ = 1/ sin2θ
sin2θ = (1 – cosθ)( 1+ cosθ)
If cos2θ is divide throughout:
tan2 θ + 1 = 1/ cos2θ.
Express cos θ in terms of sine and tan θ
Cos θ = Sin θ / tan θ
Note
sin2θ = (sin θ) 2
cos2θ = (cos θ) 2
tan2 θ = (tan θ)2
Express Sin θ in terms of cos θ and tan θ
Sin θ ≡ tan θ × cos θ
-You don’t have to memorise all these different ways of expressing trigonometric identities, through
solving many past questions, you automatically get them!

How questions are set in this section; (from Cambridge examination).
Right hand side (R.H.S) o f the equivalence
Left hand side (L.H.S) of the equivalence
-When asked to prove one side is equivalent to the other, you choose a side, either the left
hand side (L. H. S) or the right hand side (R.H.S) of the equivalence. With the use of the 2
identities (Sin θ /Cos θ ≡ tan θ and sin2θ + cos2θ ≡ 1)
How do you do it?
-Make sure you choose an easier side, from the question above it is easier starting from left hand side heading
to the right hand side. But I will solve in both ways.
-But how do I know the easy side? You look at the side that is less simplified. Detailed explanations will be made
on the video.
- I will show that left hand side is equivalence to the right hand side and in another solution I will show that the
right hand side is equivalent to the left hand side with the use of the two identities we learnt.
Techniques in attempting this kind of question. (Proving L.H.S = R.H.S)
1. What is in the side you trying to convert to, in this case we (1 – 2sin2x) it is only sine. (We will start from
the L.H.S to prove its equivalent to R.H.S).
2. What do I have on the side I am are trying to start, in this case we have only tan2x.
3. Is there a relation between tan and sin? Is there a way I can express tan2x in terms of sine? Use the
identities (on previous page).

SOLUTION OF TRIGONOMETRICALLY EQUATION LYING IN SPECIFIC
INTERVAL
1. Interval may be positive or negative
-Can you tell the difference between cos 60 and cos -60?
This is anti-clockwise
(60o), means you start from 0o
going anti-clockwise
+60
-60
(-60o )means you start form 0o
clockwise. That means
cos-60o = cos 300o
This is clockwise
Does this make any sense?

1. Cos -120 = cos 240 = - cos 60
2. Sin 300 = sin -60 = -sin 60
For tangent it is different, but trust me! If you understand it, forgetting is hard.
-All this will be explained clearly on the video for this section.
1.1 When interval is positive
According to how we have learnt, cosine is positive in the 1st and 4th quadrant.
Meaning, cos60 =cos 300= 0.5
- If a question is given as cos x = 0.5, find x. such that 0o< x < 360o
Answer: x is 60o and 300o
Let me change the interval
This means, the value of x you will get
should be somewhere between
0 – 360.
Interval
- If a question is given as cos x = 0.5, find x. such that 0o< x < 180o
Answer: x = 60o only
300o is eliminated as the answer
because it is not in the specified
interval. X should be somewhere
between 0o – 180o.

1.2 When interval is negative.
-If a question is given as cos x = 0.5, find x. Such that -180o< x < 180
+180 x is 60o and 300o – only 60o is in the
interval.
But we have also learnt that 300o can
be written as -60o .
Therefore x is 60o and -60o
+180
-180

Conceptual questions
1. Can you draw a sine and a cosine graph? What is the similarities
and difference?
2. What is the difference between a tangent graph, cosine and sine
in terms of period of completing a cycle?
3. State the effect on the graph on changing the following variable
on the equation, y=asin bx + d
3.1 Increasing “a”
3.2 Changing “d”
3.3 Doubling “b”
3.4 Making “a” negative.
4. State the reference angles of the following angles
4.1 240o
4.2 210o
4.3 60o
5. List down the ways of finding the exact value of a certain angle.
5.1 find the exact value of the following angles
5.1.1 60o
5.1.2 240o
5.1.3 120o
6. Mention two identities that you have learnt.
7. Express the identities mentioned in question 6 to obtain at least
3 different equivalences.
(DISCUSS THE ABOVE QUESTIONS WITH YOUR TEACHER/TUTOR)

AS LEVEL Trigonometry (CIE) EXPLAINED WITH EXAMPLE AND DIAGRAMS

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (20)

Similar to AS LEVEL Trigonometry (CIE) EXPLAINED WITH EXAMPLE AND DIAGRAMS

Similar to AS LEVEL Trigonometry (CIE) EXPLAINED WITH EXAMPLE AND DIAGRAMS (20)

More from RACSOelimu

More from RACSOelimu (7)

AS LEVEL Trigonometry (CIE) EXPLAINED WITH EXAMPLE AND DIAGRAMS