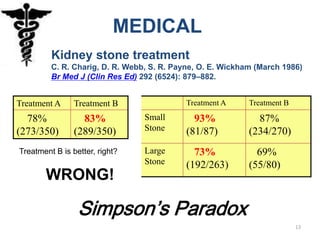
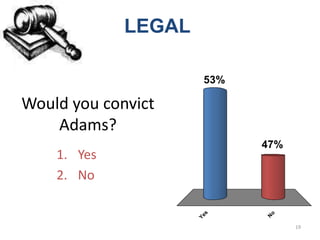
Based on the information provided, I would not convict Adams. While the DNA evidence places him in a very small group of potential suspects, there are reasonable doubts raised by the defense arguments regarding the accuracy of the victim's identification and Adams' alibi. Statistical evidence alone is not enough to determine guilt beyond a reasonable doubt in this case.

2. A type of mathematical analysis
involving the use of quantified
representations, models and
summaries for a given set of empirical
data or real world observations.
Statistical analysis involves the process
of collecting and analyzing data and then
summarizing the data into a numerical
form.

3. Statistics is a general term used to summarize a
process that an analyst, mathematician or
statistician can use to characterize a data set. If
the data set is based on a sample of a larger
population, then the analyst can extend
inferences onto the population based on the
statistical results from the sample.
Some statistical measures include regression
analysis, mean, kurtosis, skewness, analysis of
variance and variance.

4. Gottfried Achenwall used the word statistik at a German University in 1749 which
means that political science of different countries. In 1771 W. Hooper
(Englishman) usedthe word statistics in his translation of Elements of Universal
Erudition written by Baron B.F Bieford, in his book statistics has been defined as
the science that teaches us what is the political arrangement of all the modern
states of the known world. There is a big gap between the old statistics and the
modern statistics, but old statistics also used as a part of the present statistics.
During the 18th century the English writer have used the word statistics in their
works, so statistics has developed gradually during last few centuries. A lot of work
has been done in the end of the nineteenth century.
At the beginning of the 20th century, William S Gosset was developed the
methods for decision making based on small set of data. During the 20th century
several statistician are active in developing new methods, theories and application
of statistics. Now these days the availability of electronics computers is certainly a
major factor in the modern development of statistics.

5. Types of Data:
Attribute:
Discrete data. Data values can only be integers. Counted data or
attribute data. Examples include:
 How many of the products are defective?
 How often are the machines repaired?
 How many people are absent each day?
Variable:
Continuous data. Data values can be any real number.
Measured data.
Examples include:
 How long is each item?
 How long did it take to complete the task?
 What is the weight of the product?
 Length, volume, time

6. MEAN MEDIAN MODE
• The quotient of the • Denoting or • The mode in a list
sum of several relating to a value of numbers refers
quantities and their or quantity lying at to the list of
number; an the midpoint of a numbers that occur
average. frequency most frequently.
distribution of
observed values or
quantities

7. FREQUENCY
DISTRIBUTION
GROUPED UNGROUPED

8. Grouped frequency distributions
Can be used when the range of values
in the data set is very large. The data
must be grouped into classes that are
more than one unit in width.
Examples - the life of boat batteries in
hours.

9. Ungrouped frequency distributions
Ungrouped frequency distributions - can be used
for data that can be enumerated and when the
range of values in the data set is not large.
Examples - number of miles your instructors
have to travel from home to campus, number of
girls in a 4-child family etc.

10. 10

11. FINANCE
•What do you want to
learn from this data?
• How do you
summarize the data?
• How do you visualize
the signal behind the
noise?
11

12. MEDICAL
• How do you test whether a new drug is
effective?
• Ideally, we perform a controlled clinical trial, by
randomly assign one group of people to take the
drug, and another group to take a placebo.
• It needs to be double blinded.
• When such an experiment is not possible due to
practical or ethical issues, what can go wrong?
12

13. MEDICAL
Kidney stone treatment
C. R. Charig, D. R. Webb, S. R. Payne, O. E. Wickham (March 1986)
Br Med J (Clin Res Ed) 292 (6524): 879–882.
Treatment A Treatment B Treatment A Treatment B
78% 83% Small 93% 87%
(273/350) (289/350) Stone (81/87) (234/270)
Treatment B is better, right? Large 73% 69%
Stone (192/263) (55/80)
WRONG!
Simpson’s Paradox
13

14. LEGAL
• How is statistics an important part of our legal
system?
• How might we use a statistic or probability as
evidence in a trial?
• How are statistics often misinterpreted by
lawyers and juries?
14

15. LEGAL
You have just been selected for jury duty. In 1996 in
England, Denis Adams was suspect in a rape trial.
Listen closely to the details of the case and the
arguments presented before deciding your verdict.
(We have simplified the actual case/arguments for the
purpose of this illustration.)
15

16. LEGAL
Prosecution Argument
• Adams’ DNA profile matches that of evidence found
at the scene of the crime
•If Adams is innocent, there is only a 1 in 20 million
chance that his DNA would match that found at the
crime
• Therefore, the probability Adams is innocent is only
.00000005, hence the probability he is guilty is 1
minus that, .9999995. Thus Adams is guilty beyond
the shadow of a doubt.
16

17. LEGAL
Defense Argument
• If the odds of a DNA match for any person is
1/ 20,000,000, since there are 60 million people in
England, there are on average 3 other people with this
DNA type (in 1996).
•Since it is equally likely to be any of these others, the
probability of Adams’ guilt is 1/3 = .33, which is not
enough certainty to convict.
17

18. LEGAL
Defense Argument
• In an identity line up, victim failed to pick out Adams
• Victim describes an attacker in his 20’s
• Adams is 37
• Victim guessed Adams to be about 40
• Adams had an alibi for the night of the crime (he
spent the night with his girlfriend)
18

19. LEGAL
53%
Would you convict
Adams?
47%
1. Yes
2. No
s
o
Ye
N
19