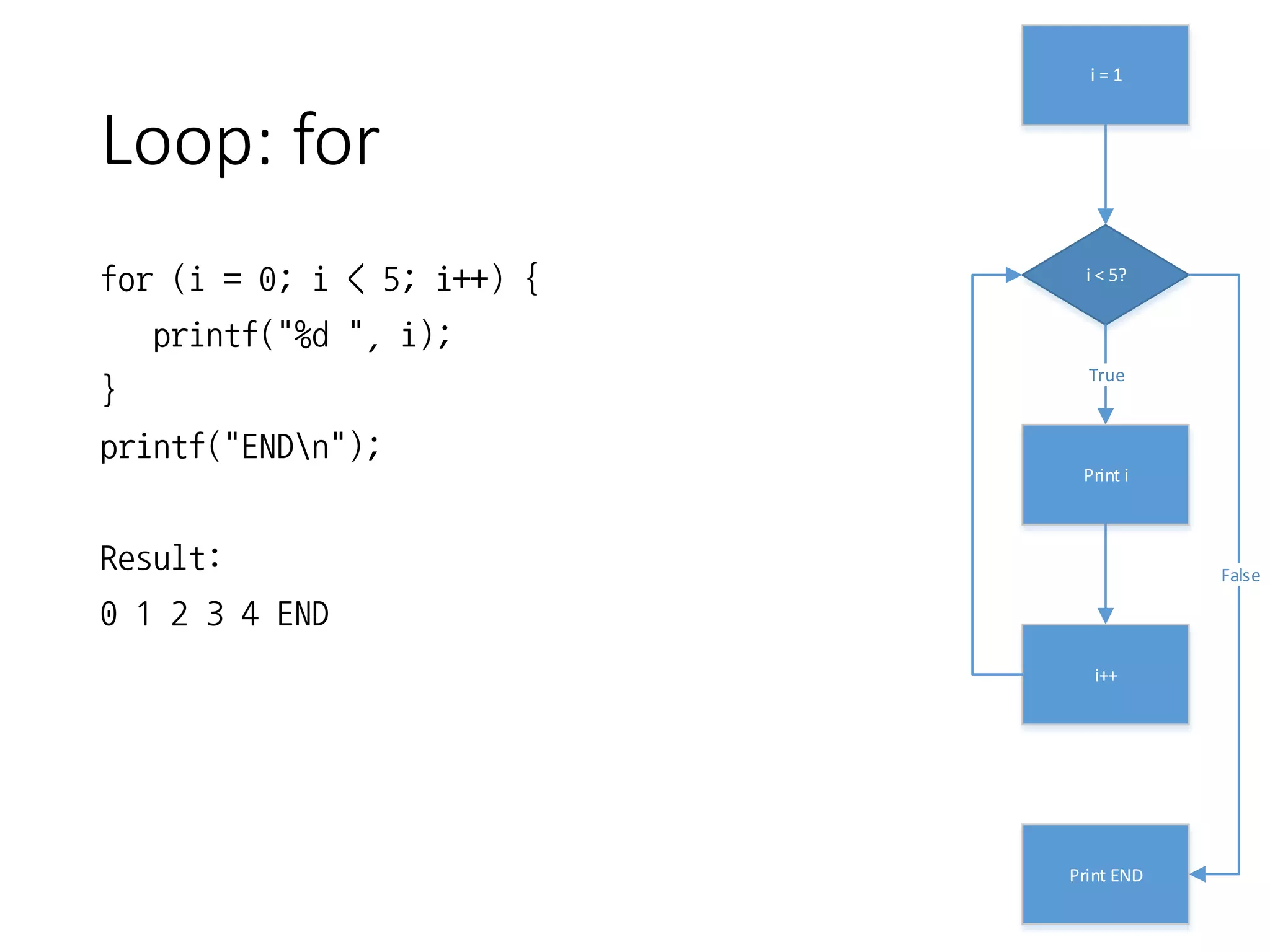
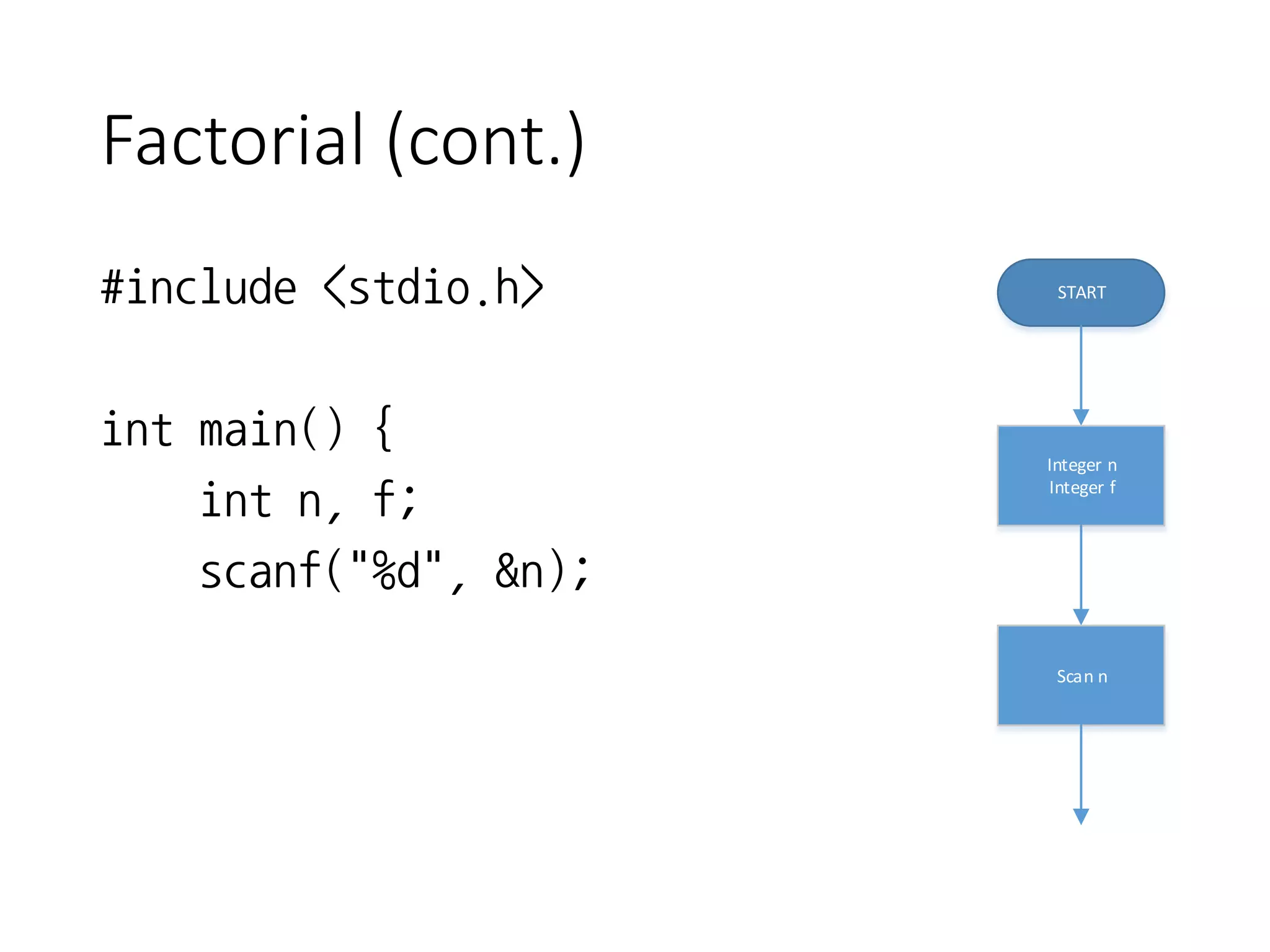
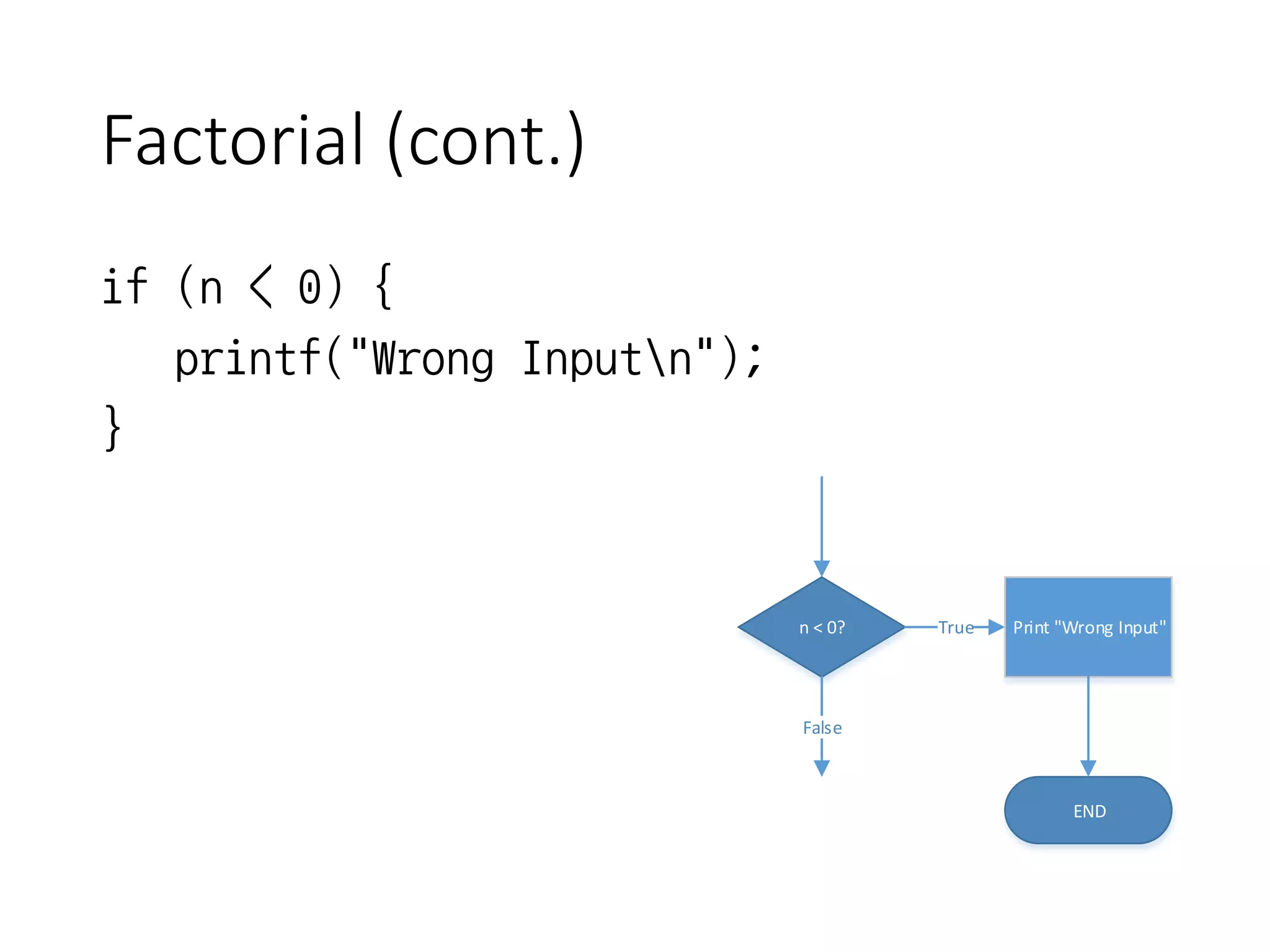
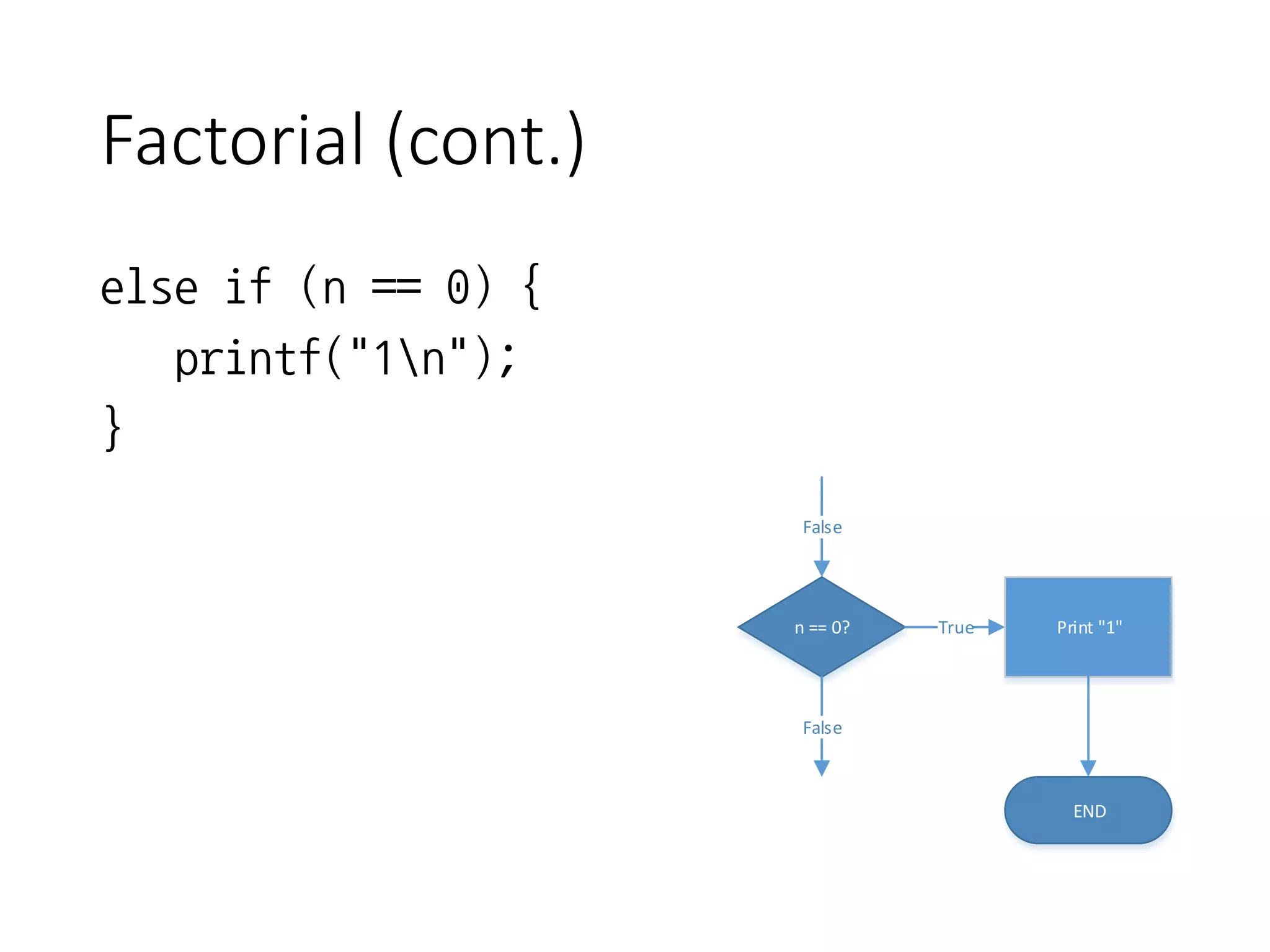
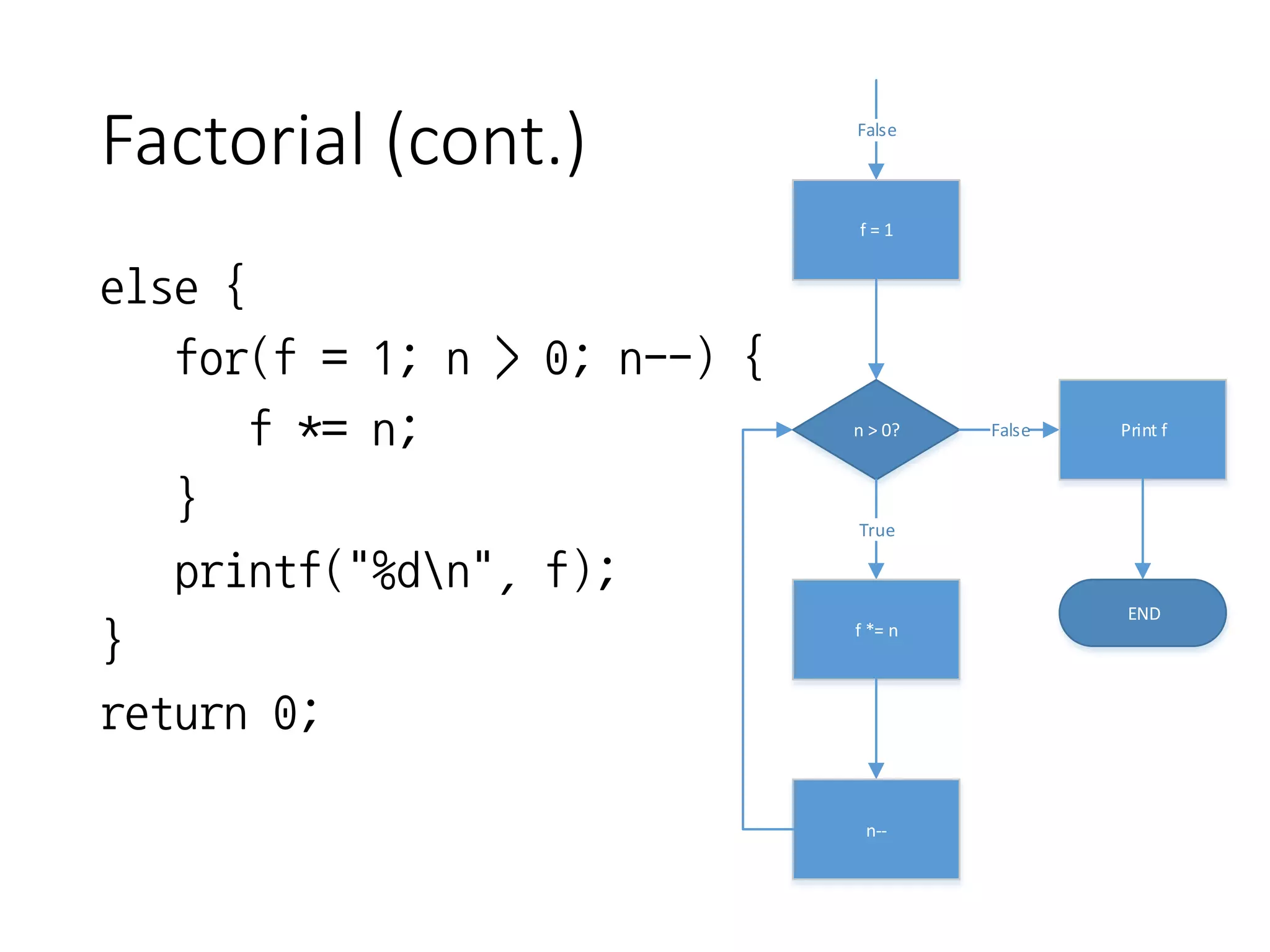
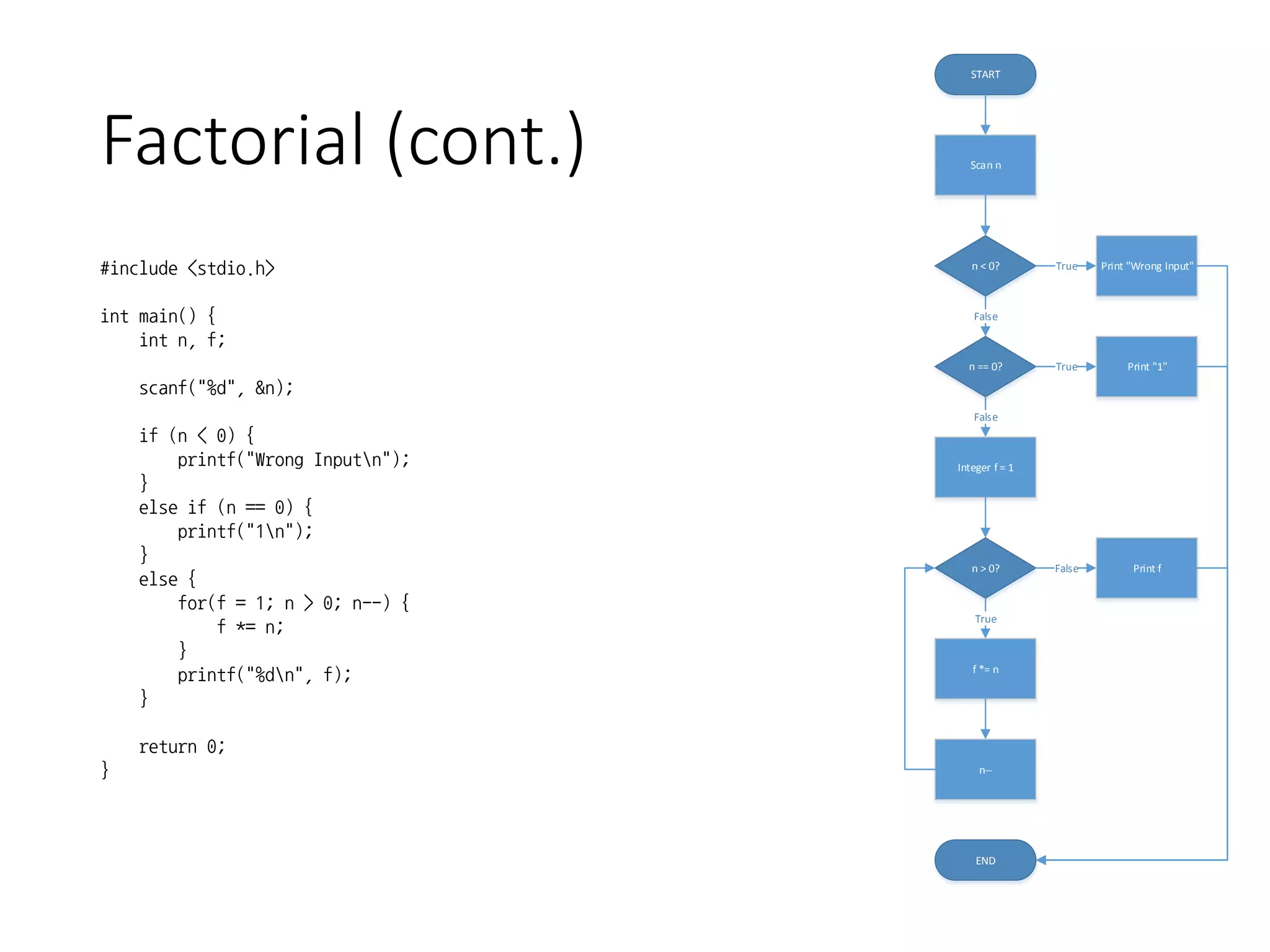
The document provides examples and explanations for various programming concepts: - It explains for loops with examples of printing numbers from 0 to 4. - It shows functions like pow(), sqrt(), and includes their prototypes. Examples calculate 2^3 and square root of 2. - It outlines a factorial program that takes user input, checks for invalid input, and calculates the factorial using a for loop. - It discusses improving the factorial program to handle larger numbers using long long int. - It provides examples of programming practice problems to find odd numbers between ranges, divisors of a number, perfect numbers, and Pythagorean triples.

1. Practice
Week 3

2. Loop: for
for (initialization; condition; increment) {
// statement1
}
// statement2
Initialization
Condition
True
Statement 1
Increment
False
Statement 2

3. Loop: for
for (i = 0; i < 5; i++) {
printf("%d ", i);
}
printf("ENDn");
Result:
0 1 2 3 4 END
i = 1
i < 5?
True
Print i
i++
False
Print END

4. 𝑥 𝑦
• double pow(double x, double y);
• float powf(float x, float y);
• long double pow(long double x, long double y);
#include <stdio.h>
#include <math.h>
int main() {
int x = 2;
int y = 3;
printf("%dn", (int)pow((double)x, (double)y)); // 2^3
printf("%.3lfn", pow((double)x, 0.5)); //√2
return 0;
}

5. 𝑥
• double sqrt(double x);
• float sqrtf(float x);
• long double sqrtl(long double x);
#include <stdio.h>
#include <math.h>
int main() {
double a = 3.0;
printf("%lf", sqrt(a));
return 0;
}

6. Factorial
𝑛! = 1 × 2 × ⋯ × 𝑛
0! = 1
𝑛 𝑖𝑠 𝑝𝑜𝑠𝑖𝑡𝑖𝑣𝑒 𝑖𝑛𝑡𝑒𝑔𝑒𝑟
Input
Integer n
Output
Print the value of n!
If n < 0, Print “Wrong Input”

7. Factorial (cont.)
#include <stdio.h>
int main() {
int n, f;
scanf("%d", &n);
START
Integer n
Integer f
Scan n

8. Factorial (cont.)
if (n < 0) {
printf("Wrong Inputn");
}
n < 0? True Print "Wrong Input"
END
False

9. Factorial (cont.)
else if (n == 0) {
printf("1n");
}
False
n == 0? True Print "1"
False
END

10. Factorial (cont.)
else {
for(f = 1; n > 0; n--) {
f *= n;
}
printf("%dn", f);
}
return 0;
False
f = 1
n > 0? False Print f
END
True
f *= n
n--

11. Factorial (cont.)
#include <stdio.h>
int main() {
int n, f;
scanf("%d", &n);
if (n < 0) {
printf("Wrong Inputn");
}
else if (n == 0) {
printf("1n");
}
else {
for(f = 1; n > 0; n--) {
f *= n;
}
printf("%dn", f);
}
return 0;
}
START
Scan n
n < 0?
False
n == 0? True Print "1"
True Print "Wrong Input"
False
Integer f = 1
n > 0?
True
f *= n
n--
False Print f
END

12. Factorial (cont.)
• 13! is bigger than maximum of int
• How to handle that?
• long long int is at least 64 bits.

13. Practice 1 - Odd number
Input
Natural number a, b (a < b)
Output
Print odd numbers between a with b
Ex)
3 11
3
5
7
9
11
Input

14. Practice 2 - Divisor
Input
Natural number n (n<100,000,000)
Output
Print all divisors of n
Ex)
10
1
2
5
10
Input

15. Practice 3 - Perfect number
In number theory, a perfect number is a positive integer that is equal to
the sum of its proper positive divisors, that is, the sum of its positive
divisors excluding the number itself (also known as its aliquot sum). For
example, 6 is a perfect number. (1+2+3 = 6)
Input
Natural number n (n<2,100,000,000)
Output
If n is perfect number, print “yes”. Or if it isn’t, print “no”.
Ex-1)
6
yes
Ex-2)
8
no
Input

16. Homework - Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such
that 𝑎2 + 𝑏2 = 𝑐2. Such a triple is commonly written (a, b, c), and a well-
known example is (3, 4, 5).
Input
Natural number c (c < 45,000)
Output
Pythagorean triple (a, b, c) (a < b < c)
If there is no answer, print “impossible”.
If there are multiple answers, print all of that.
Ex-1)
5
(3, 4, 5)
Ex-2)
6
impossible
Ex-3)
25
(7, 24, 25)
(15, 20, 25)
Input