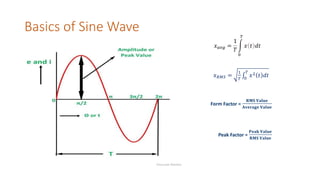
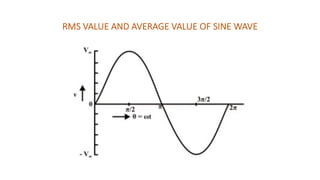
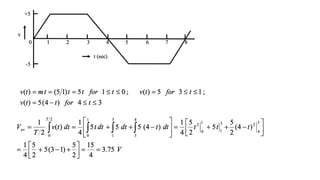
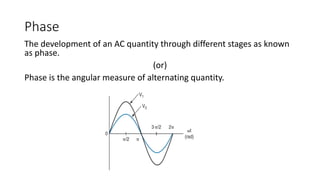
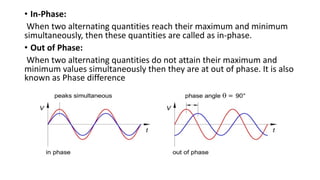
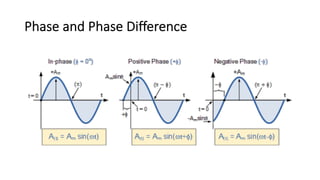
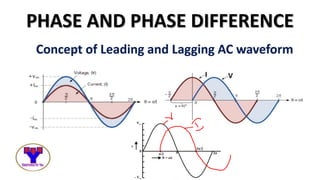
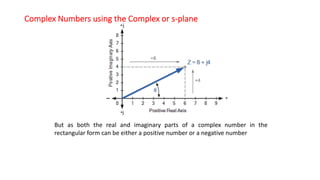
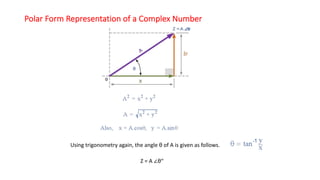
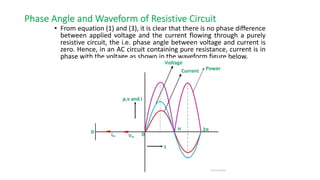
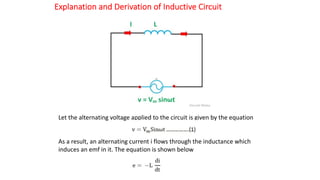
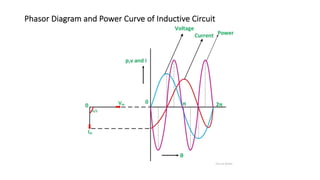
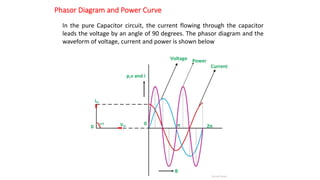
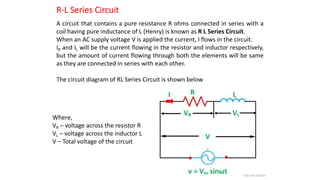
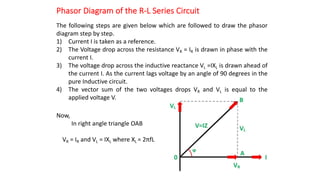
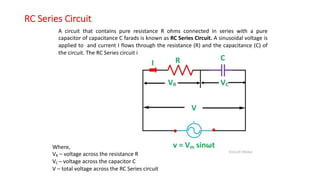
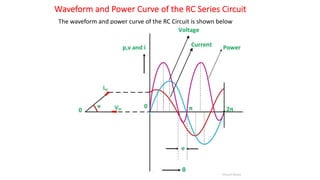
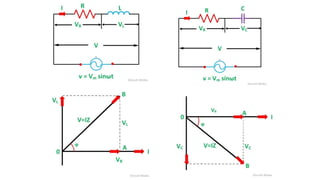
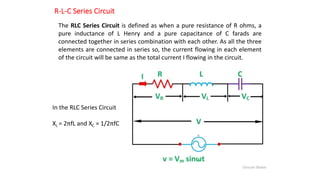
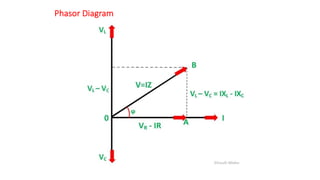
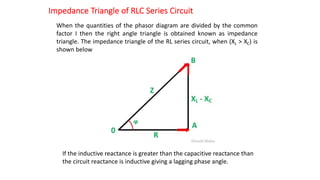
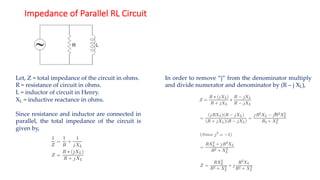
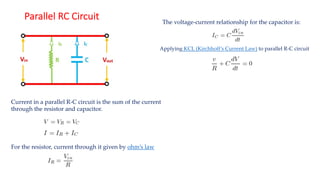
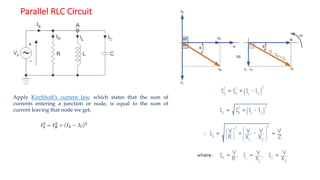
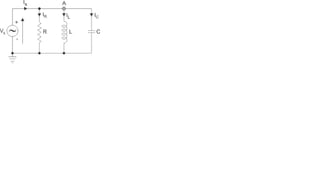
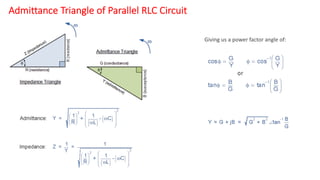
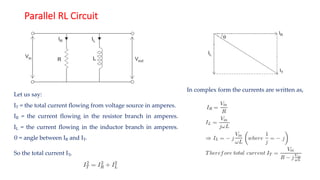
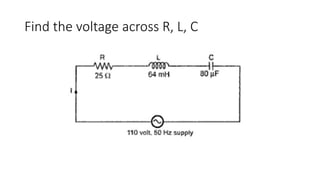
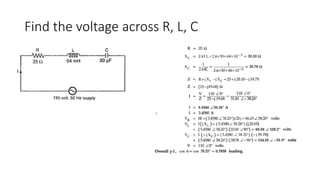
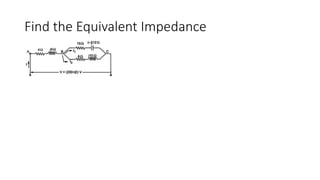
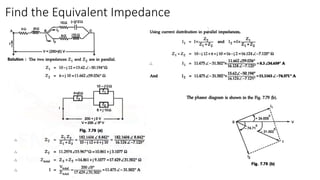
The document covers single-phase alternating current (AC) circuits, focusing on concepts such as RMS values, impedance, reactance, and phase relationships in resistive, inductive, and capacitive circuits. It explains the behavior of current and voltage in RL, RC, and RLC series circuits, highlighting the differences in power factor and phase angles. Key mathematical principles and graphical representations such as phasor diagrams and impedance triangles are utilized to illustrate circuit characteristics and power consumption.