Downloaded 154 times
Uploaded byEY GDS
Unit 2 resonance circuit
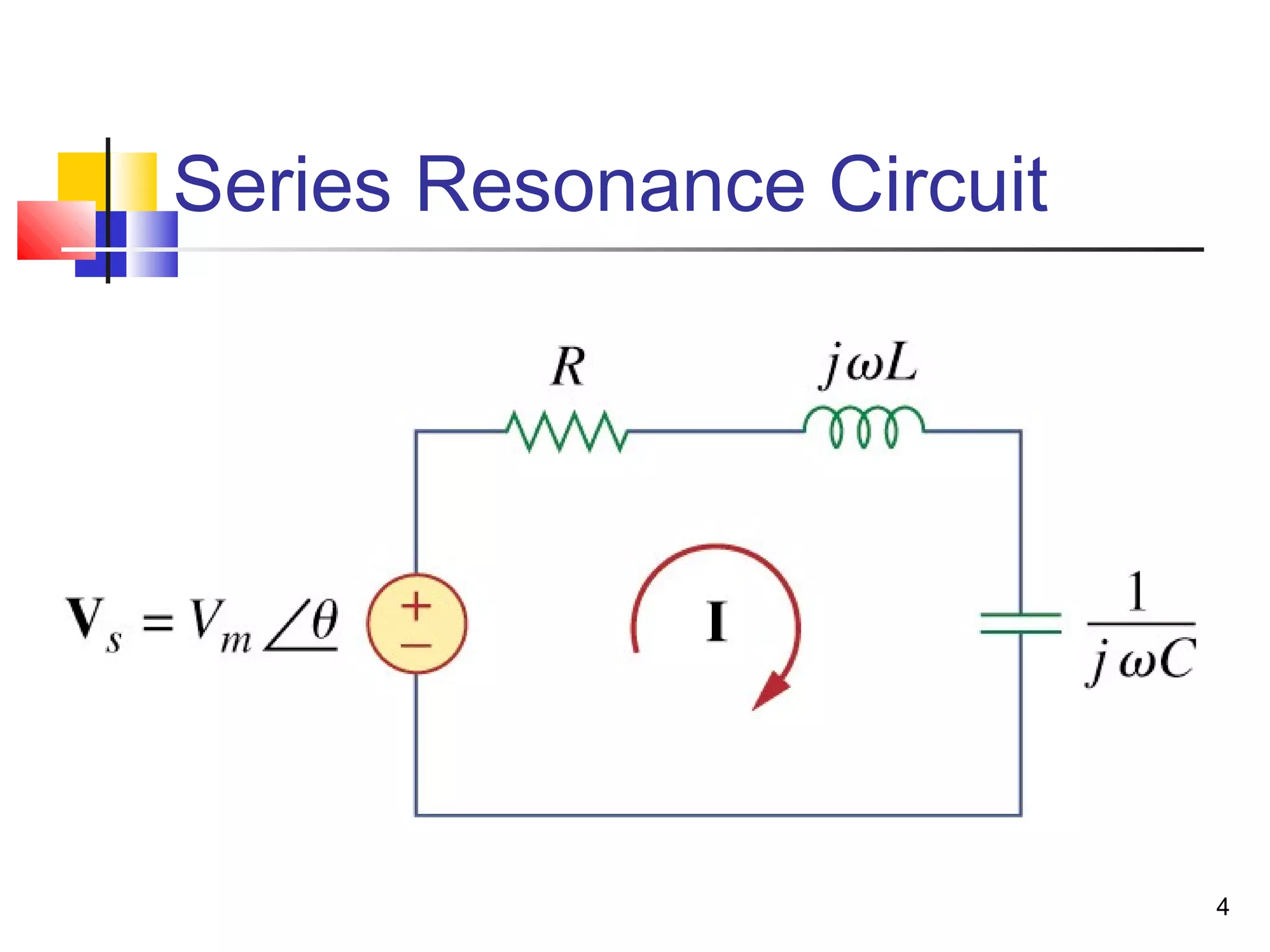
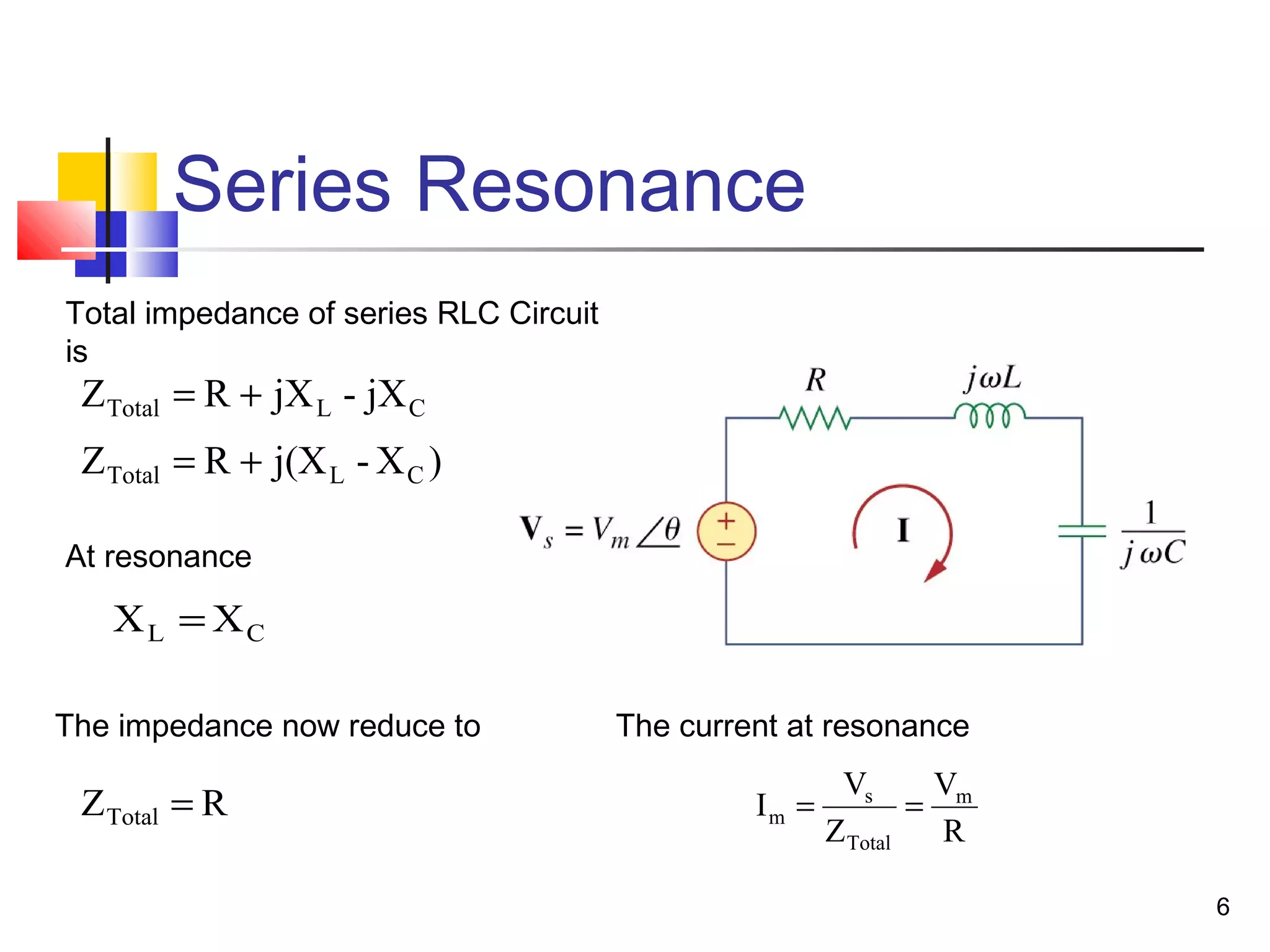
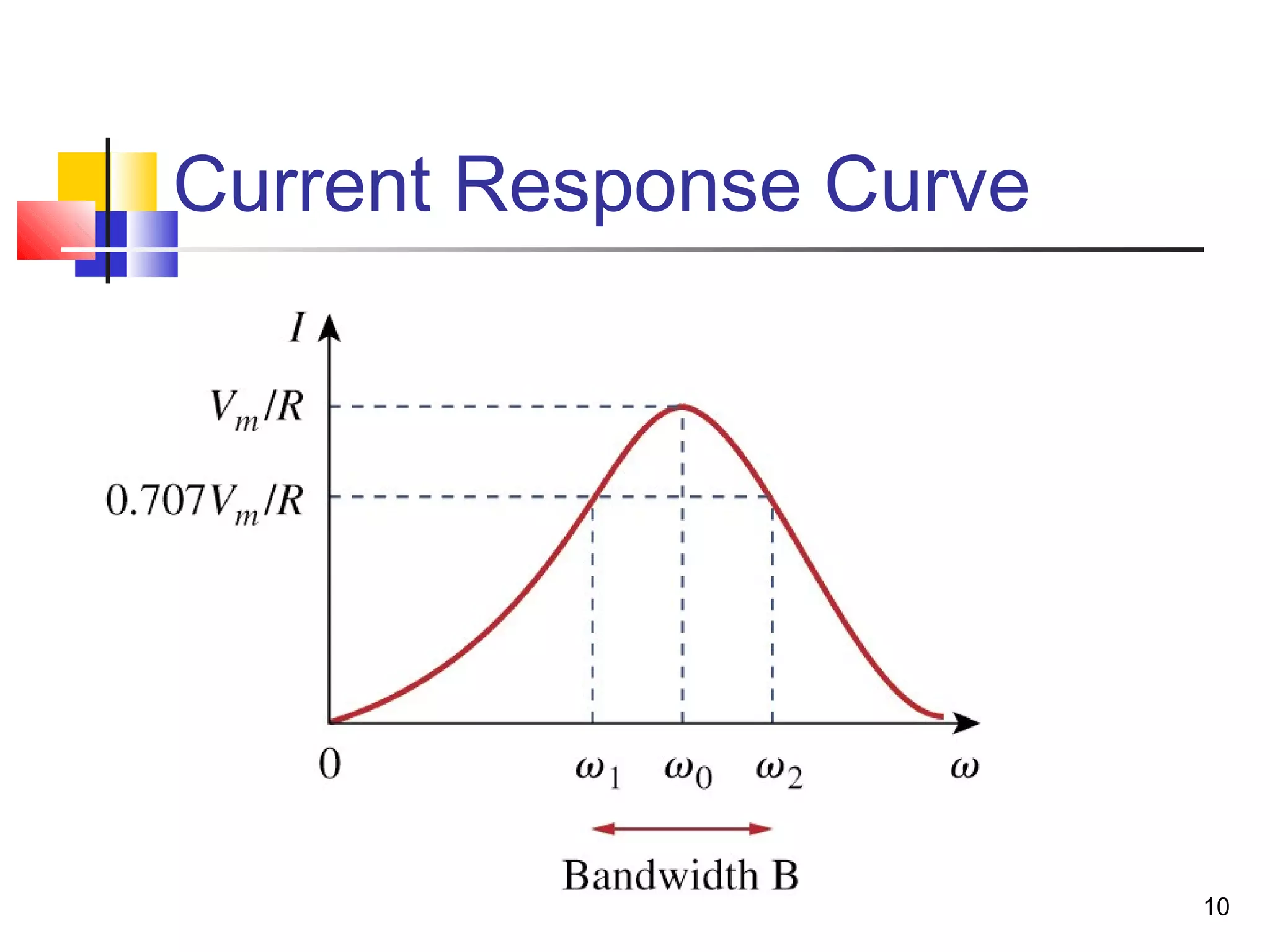
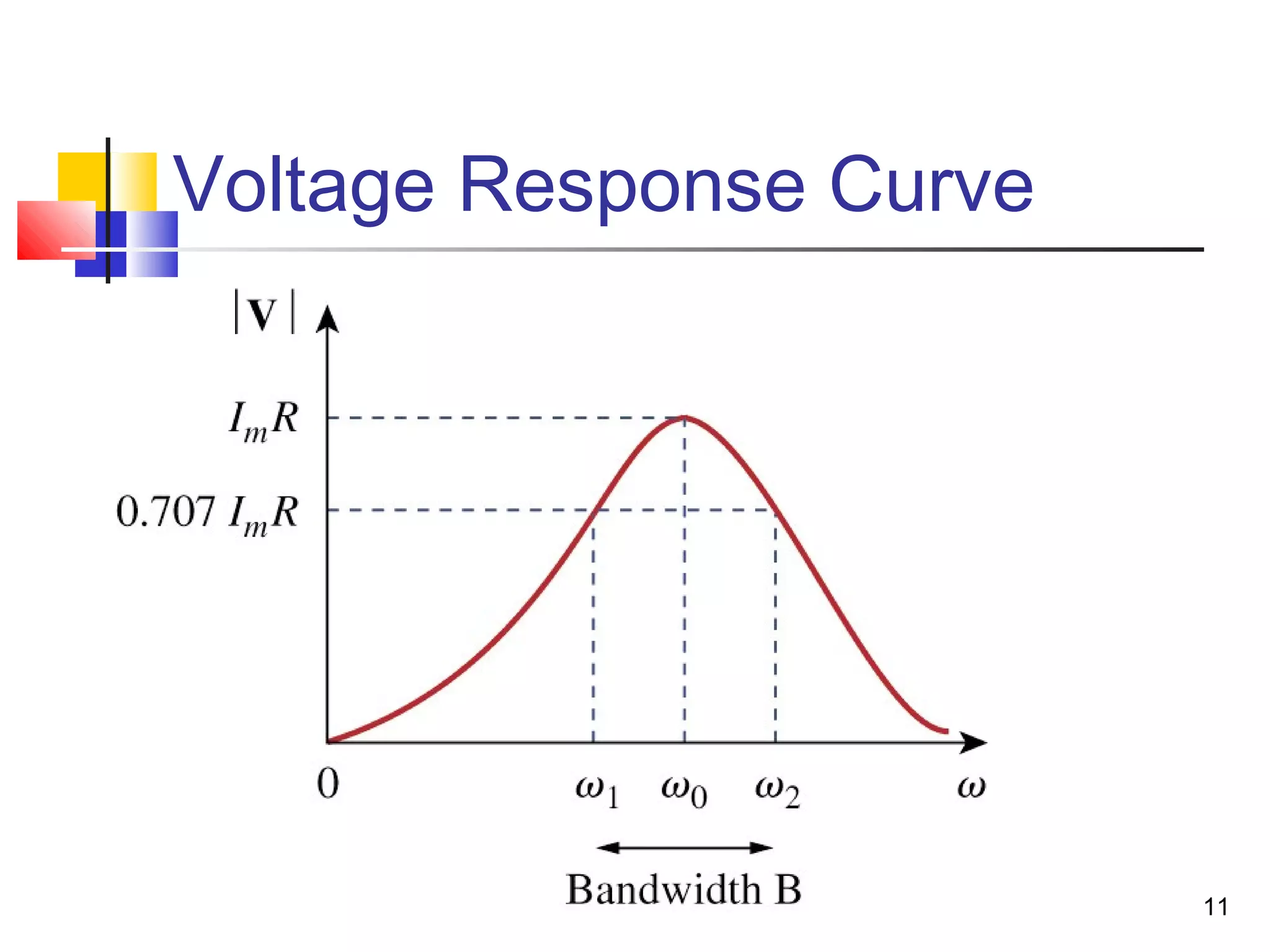
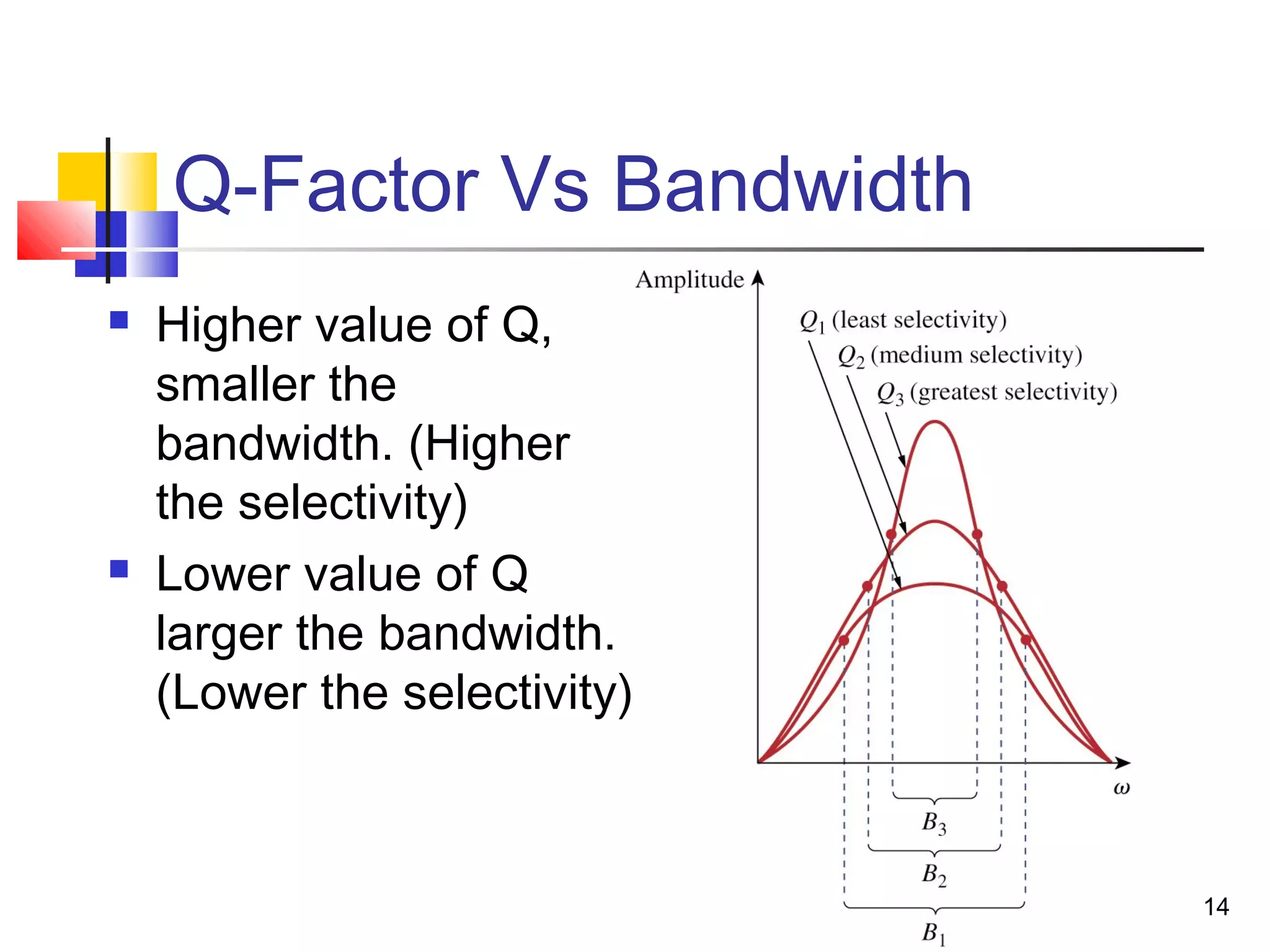
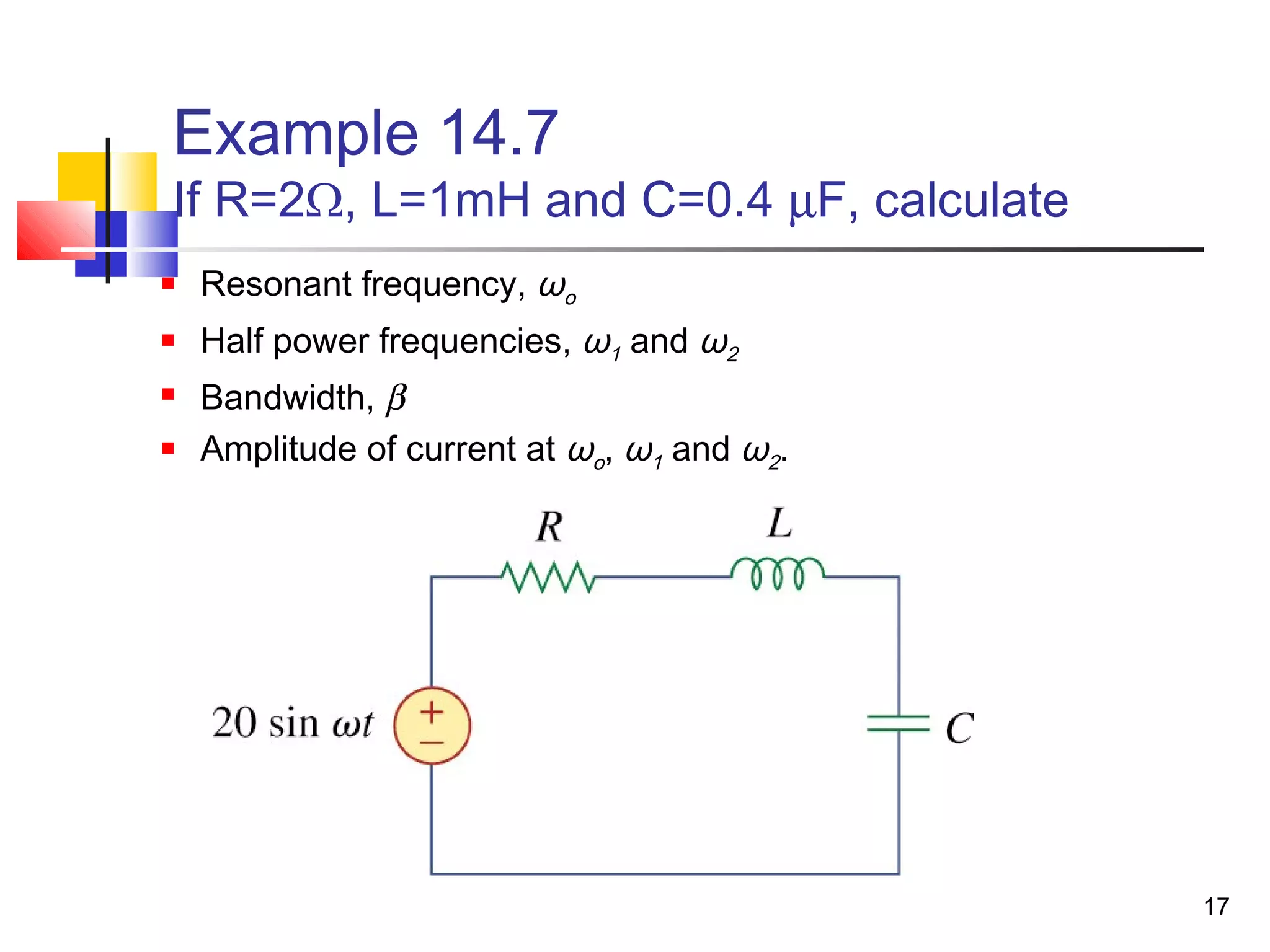
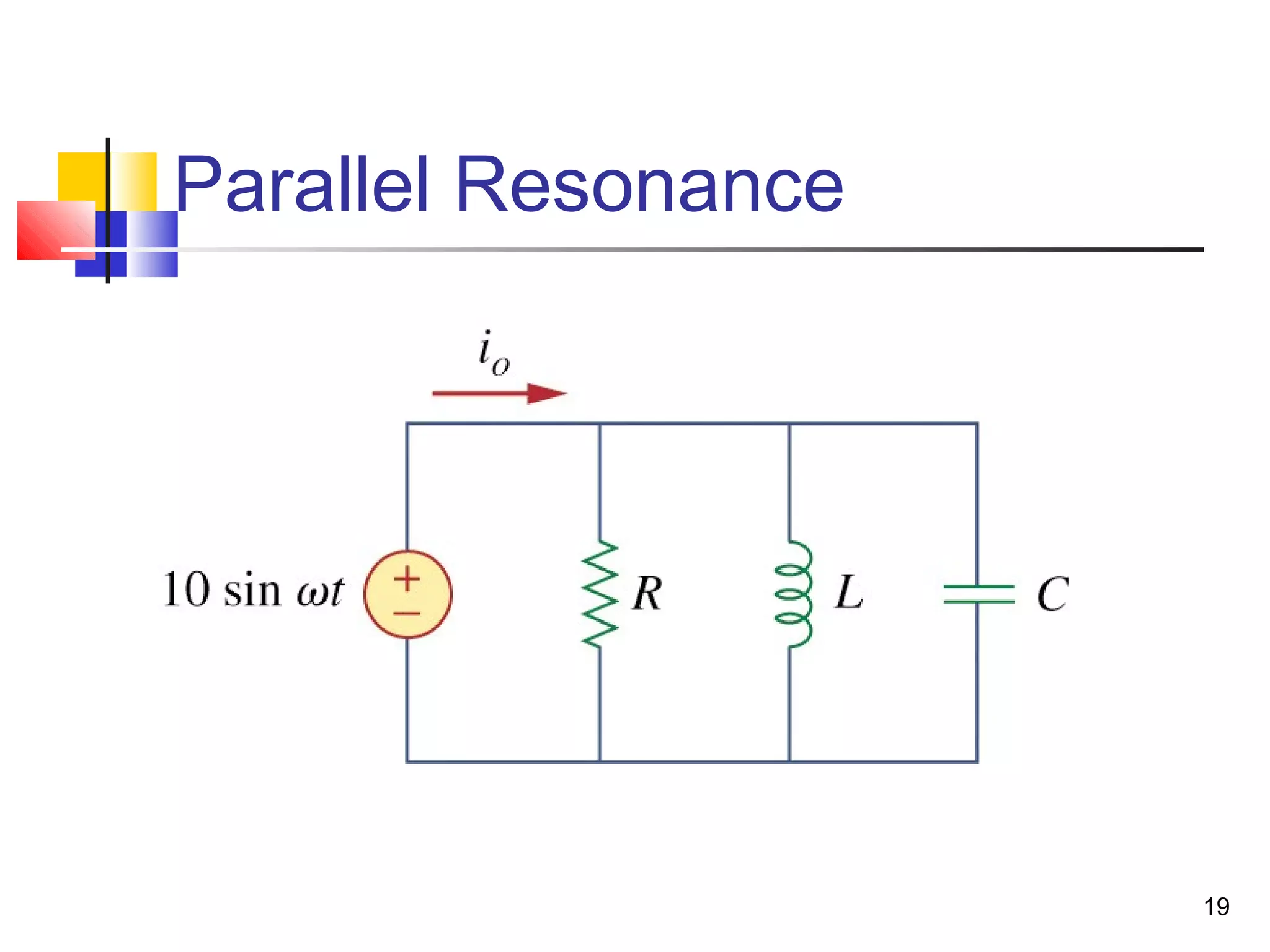
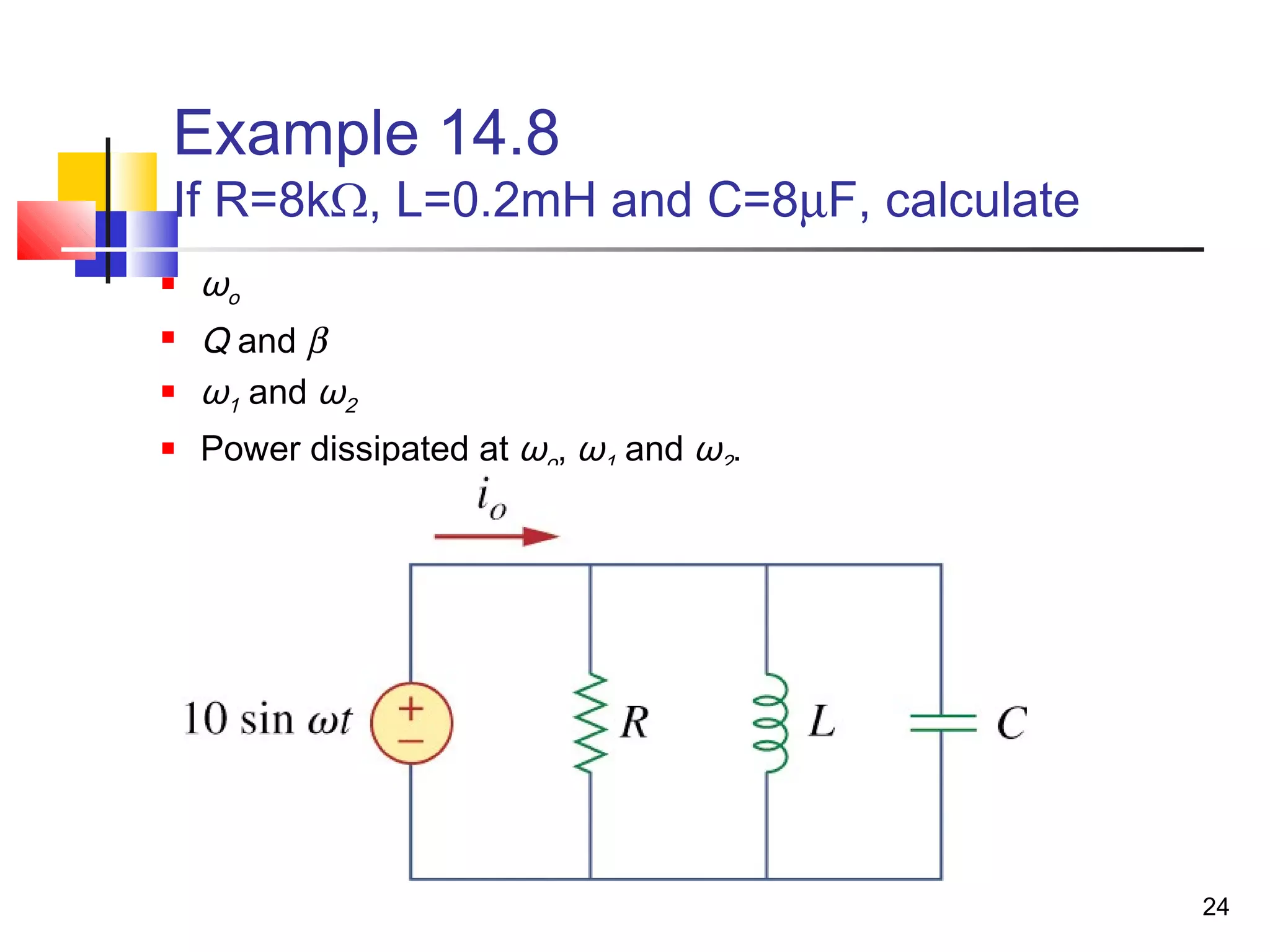
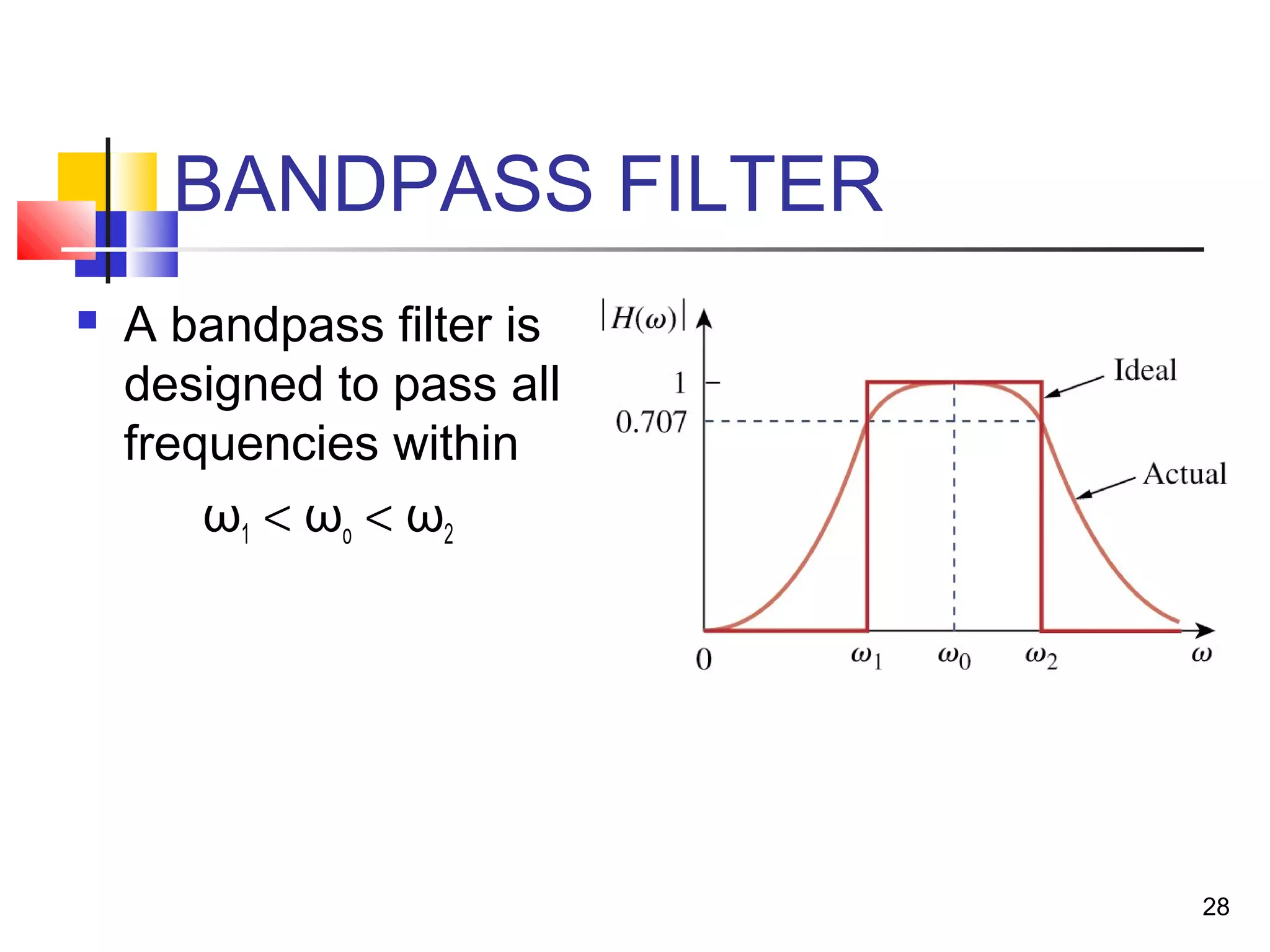
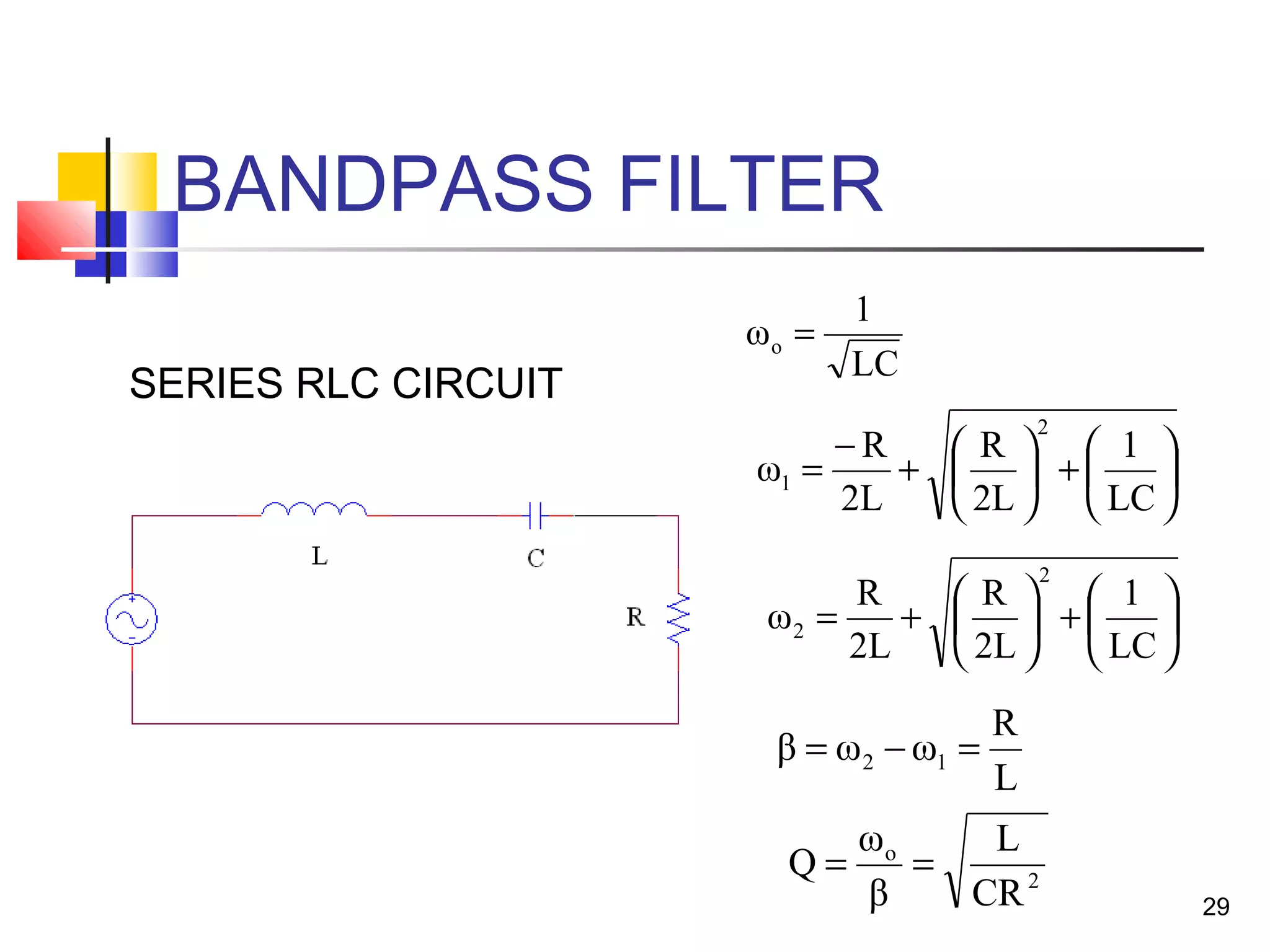
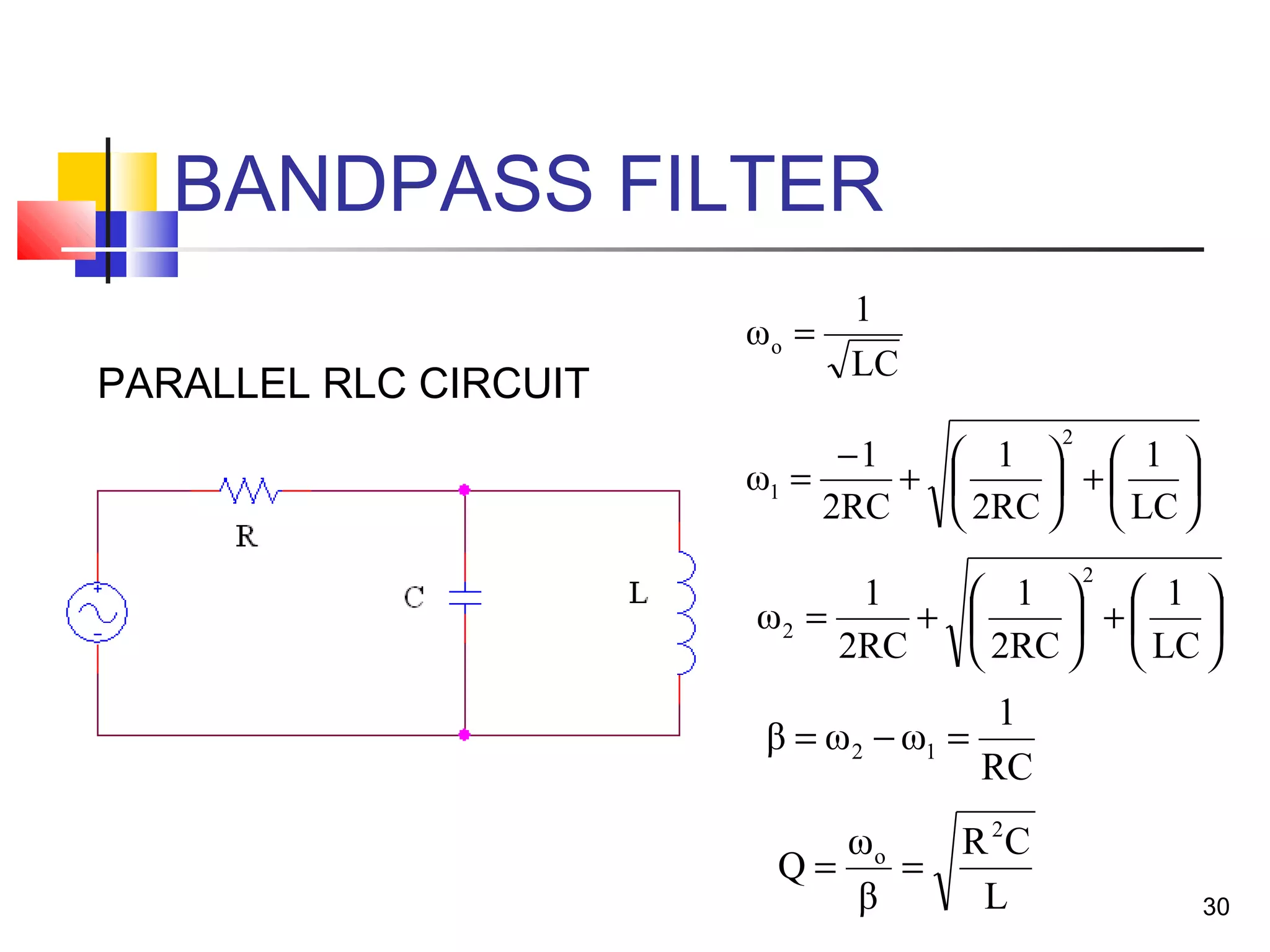
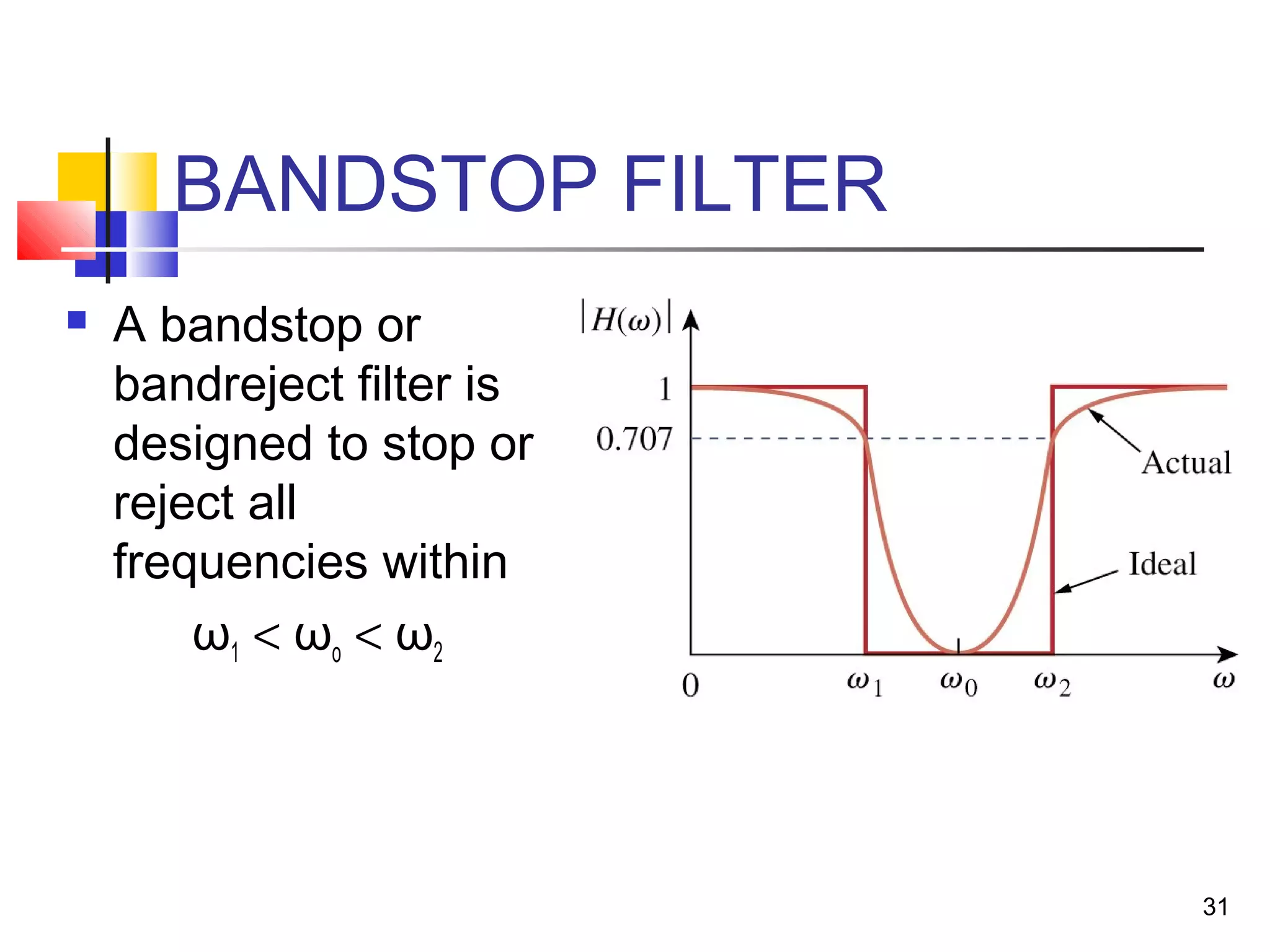
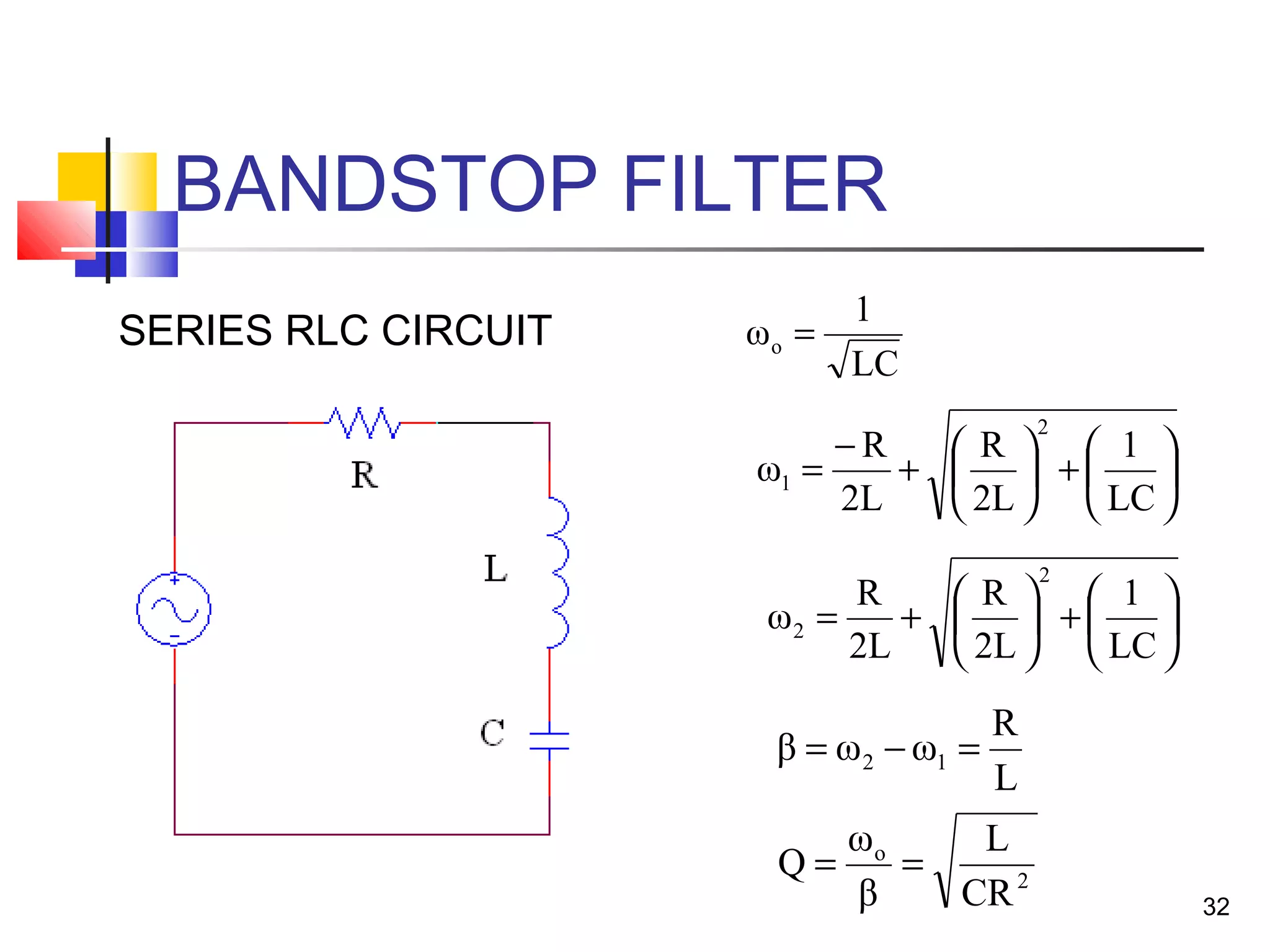
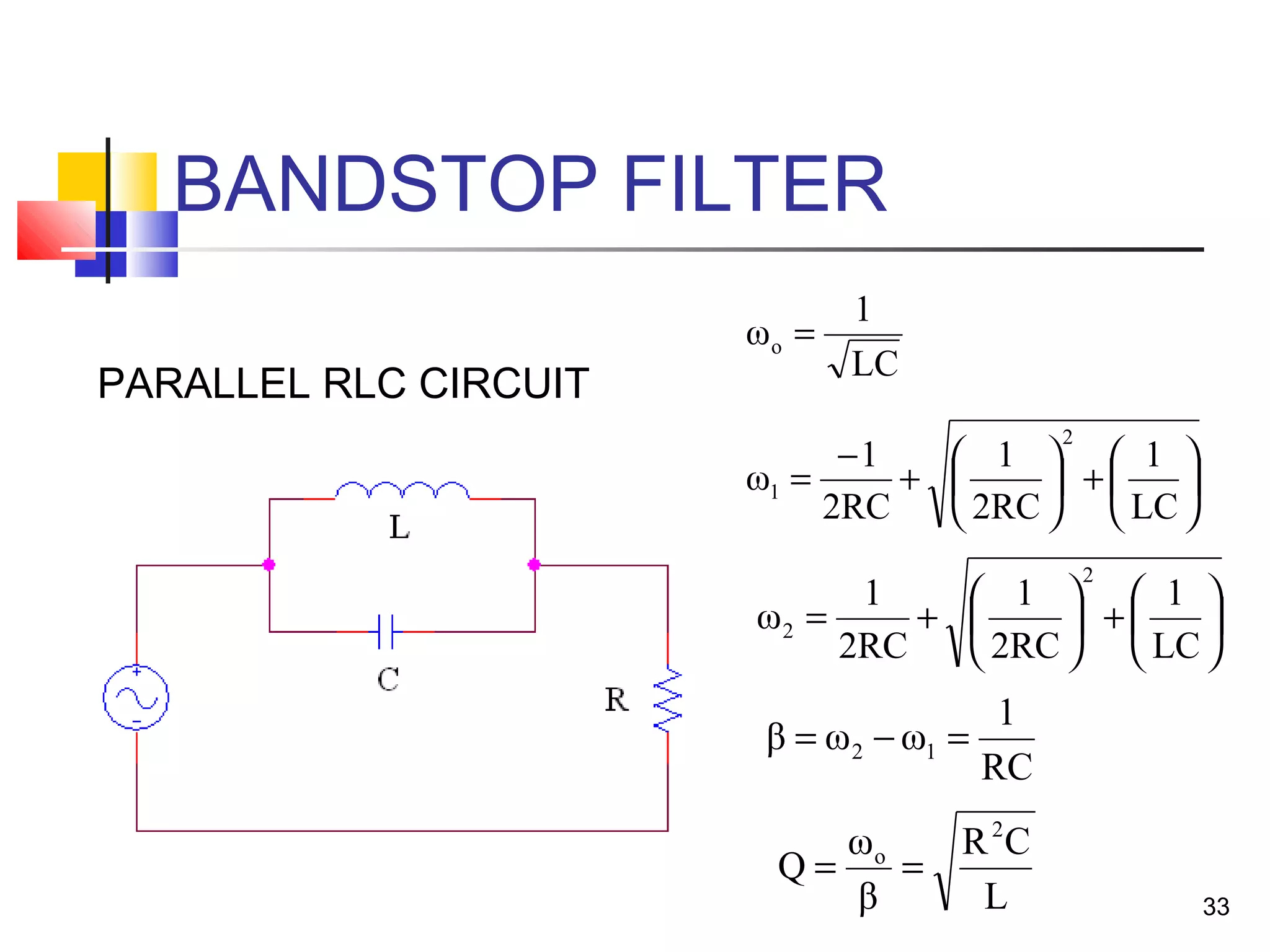
This document discusses resonance circuits and their applications. Resonance occurs when the capacitive and inductive reactances are equal, resulting in a purely resistive impedance. Key parameters of resonance circuits include the resonance frequency, half-power frequencies, bandwidth, and quality factor. Resonance circuits are useful for constructing filters and are used in applications like bandpass and bandstop filters, which allow only certain frequency ranges to pass.
More Related Content
Similar to Unit 2 resonance circuit
Unit 2 resonance circuit
- 1. UNIT-2 RESONANCE CIRCUITS 1.selectivity 2.sensitivity 3.fidelity D VS Ramanjaneyulu Asst.professor Department ofECE, Ace engineering college.
- 2. 2 Content Series Resonance Parallel Resonance Important Parameters Resonance Frequency, ω0 Half-power frequencies, ω1 and ω2 Bandwidth, β Quality Factor, Q Application
- 3. 3 Introduction Resonance isa condition in an RLC circuit in which the capacitive and reactive reactance are equal in magnitude, thereby resulting in a purely resistive impedance. Resonance circuits are useful for constructing filters and used in many application.
- 4.
- 5. 5 At Resonance Atresonance, the impedance consists only resistive component R. The value of current will be maximum since the total impedance is minimum. The voltage and current are in phase. Maximum power occurs at resonance since the power factor is unity.
- 6. 6 Series Resonance CLTotal jX-jXRZ+= R V Z V I m Total s m == Total impedance of series RLC Circuit is At resonance The impedance now reduce to CL XX = RZTotal = )X-j(XRZ CLTotal += The current at resonance
- 7. 7 Resonance Frequency Resonance frequencyis the frequency where the condition of resonance occur. Also known as center frequency. Resonance frequency rad/s LC 1 ωo = Hz LC2 1 π =of
- 8. 8 Half-power Frequency rad/s LC 1 2L R 2L R ω 2 2 + += Half-powerfrequencies is the frequency when the magnitude of the output voltage or current is decrease by the factor of 1 / √2 from its maximum value. Also known as cutoff frequencies. rad/s LC 1 2L R 2L R ω 2 1 + + − =
- 9. 9 Bandwidth, β rad/s)( 12cc ωωβ −= Bandwidth, β is define as the difference between the two half power frequencies. The width of the response curve is determine by the bandwidth. rad/s L R β =
- 10.
- 11.
- 12. 12 Quality Factor (Q-Factor) Theratio of resonance frequency to the bandwidth The “sharpness” of response curve could be measured by the quality factor, Q. R L Q oo ω β ω ==
- 13. 13 High-Q It is tobe a high-Q circuit when its quality factor is equal or greater than 10. For a high-Q circuit (Q ≥ 10), the half-power frequencies are, for all practical purposes, symmetrical around the resonant frequency and can be approximated as 2 1 β ωω −≅ o 2 2 β ωω +≅ o
- 14. 14 Q-Factor Vs Bandwidth Higher value of Q, smaller the bandwidth. (Higher the selectivity) Lower value of Q larger the bandwidth. (Lower the selectivity)
- 15. 15 Maximum Power Dissipated Theaverage power dissipated by the RLC circuit is The maximum power dissipated at resonance where R V 2 1 )P(ω m 2 o = R V I m = RI 2 1 )P(ω 2 o = Thus maximum power dissipated is
- 16. 16 Power Dissipated atω1 and ω2 At certain frequencies, where ω = ω1 and ω2, the dissipated power is half of maximum power Hence, ω1 and ω2 are called half-power frequencies. 4R V R )2/(V 2 1 )P(ω)P(ω m 22 m 21 ===
- 17. 17 Example 14.7 If R=2Ω,L=1mH and C=0.4 µF, calculate Resonant frequency, ωo Half power frequencies, ω1 and ω2 Bandwidth, β Amplitude of current at ωo, ω1 and ω2.
- 18. 18 Practice Problem 14.7 A series connected circuit has R=4Ω and L=25mH. Calculate Value of C that will produce a quality factor of 50. Find ω1 ,ω2 and β. Determine average power dissipated at ω0 , ω1 and ω2 Take Vm = 100V
- 19.
- 20. 20 Parallel Resonance The totaladmittance ωL ωC 1 = Resonance occur when )ωω L1/Cj( R 1 YTotal −+= 321Total YYYY ++= C)(-j/ 1 L)(j 1 R 1 YTotal ωω ++= Cj ωL j- R 1 YTotal ω++=
- 21. 21 At Resonance Atresonance, the impedance consists only conductance G. The value of current will be minimum since the total admittance is minimum. The voltage and current are in phase.
- 22. 22 Parameters in ParallelCircuit rad/s LC 1 2RC 1 2RC 1 ω 2 1 + + − = Parallel resonant circuit has same parameters as the series resonant circuit. rad/s LC 1 ωo = rad/s LC 1 2RC 1 2RC 1 ω 2 2 + += Resonance frequency Half-power frequencies
- 23. 23 Parameters in ParallelCircuit RC β ω Q o o ω== RC 1 12 =−= ωωβ Bandwidth Quality Factor
- 24. 24 Example 14.8 If R=8kΩ,L=0.2mH and C=8µF, calculate ωo Q and β ω1 and ω2 Power dissipated at ωo, ω1 and ω2.
- 25. 25 Practice Problem 14.8 A parallel resonant circuit has R=100kΩ, L=25mH and C=5nF. Calculate ω0 ω1 and ω2 Q β
- 26.
- 27. 27 PASSIVE FILTERS Afilter is a circuit that is designed to pass signals with desired frequencies and reject or attenuates others A filter is a Passive Filters if it consists only passive elements which is R, L and C. Filters that used resonant circuit Bandpass Filter Bandstop Filter
- 28. 28 BANDPASS FILTER Abandpass filter is designed to pass all frequencies within ω1 < ωo < ω2
- 29. 29 BANDPASS FILTER + + − = LC 1 2L R 2L R ω 2 1 SERIES RLCCIRCUIT LC 1 ωo = 2 o CR L β ω Q == L R ωωβ 12 =−= + += LC 1 2L R 2L R ω 2 2
- 30. 30 BANDPASS FILTER + + − = LC 1 2RC 1 2RC 1 ω 2 1 PARALLEL RLCCIRCUIT LC 1 ωo = L CR β ω Q 2 o == RC 1 ωωβ 12 =−= + += LC 1 2RC 1 2RC 1 ω 2 2
- 31. 31 BANDSTOP FILTER Abandstop or bandreject filter is designed to stop or reject all frequencies within ω1 < ωo < ω2
- 32. 32 BANDSTOP FILTER + + − = LC 1 2L R 2L R ω 2 1 SERIES RLCCIRCUIT LC 1 ωo = 2 o CR L β ω Q == L R ωωβ 12 =−= + += LC 1 2L R 2L R ω 2 2
- 33. 33 BANDSTOP FILTER + + − = LC 1 2RC 1 2RC 1 ω 2 1 PARALLEL RLCCIRCUIT LC 1 ωo = L CR β ω Q 2 o == RC 1 ωωβ 12 =−= + += LC 1 2RC 1 2RC 1 ω 2 2