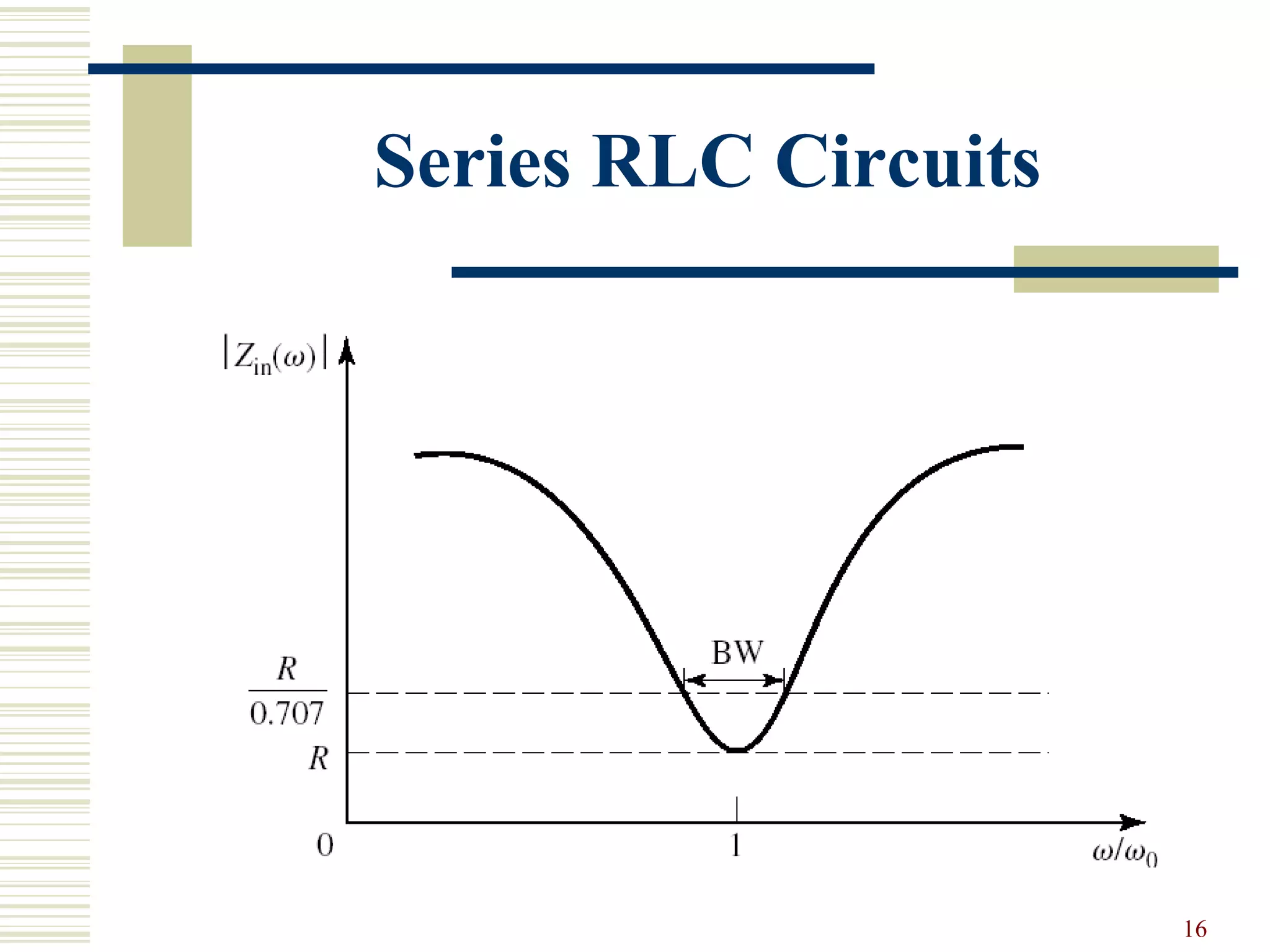
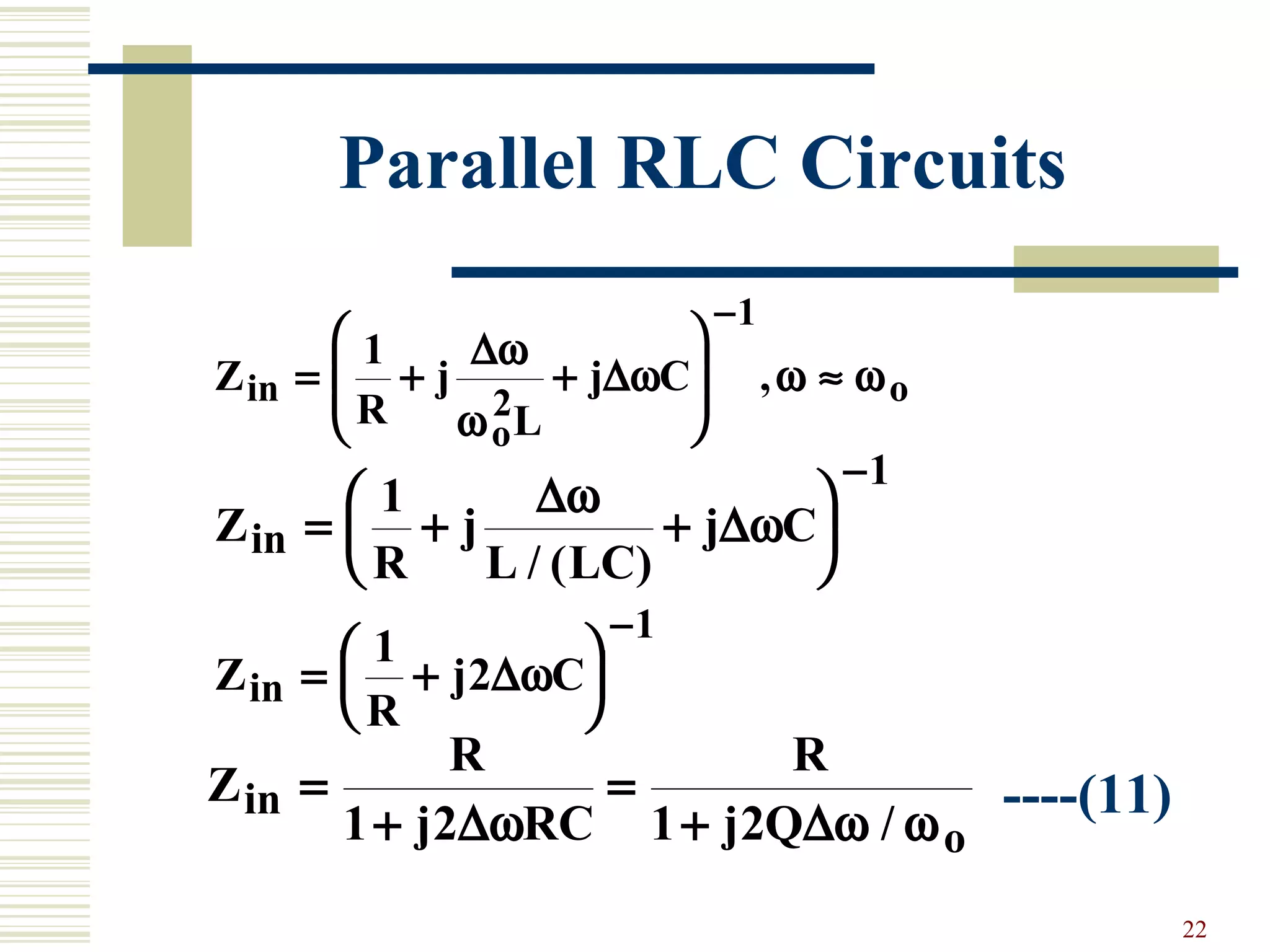
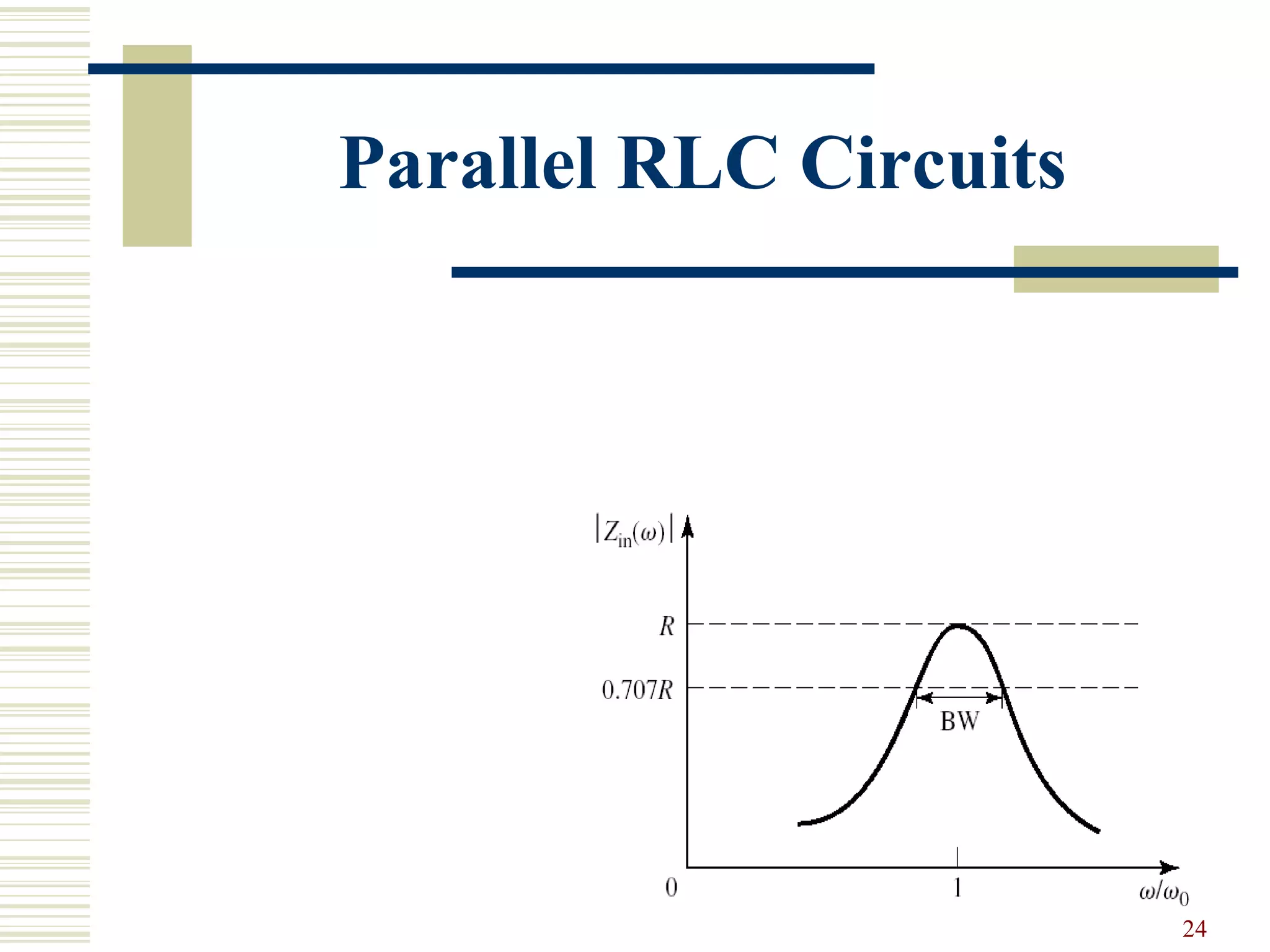
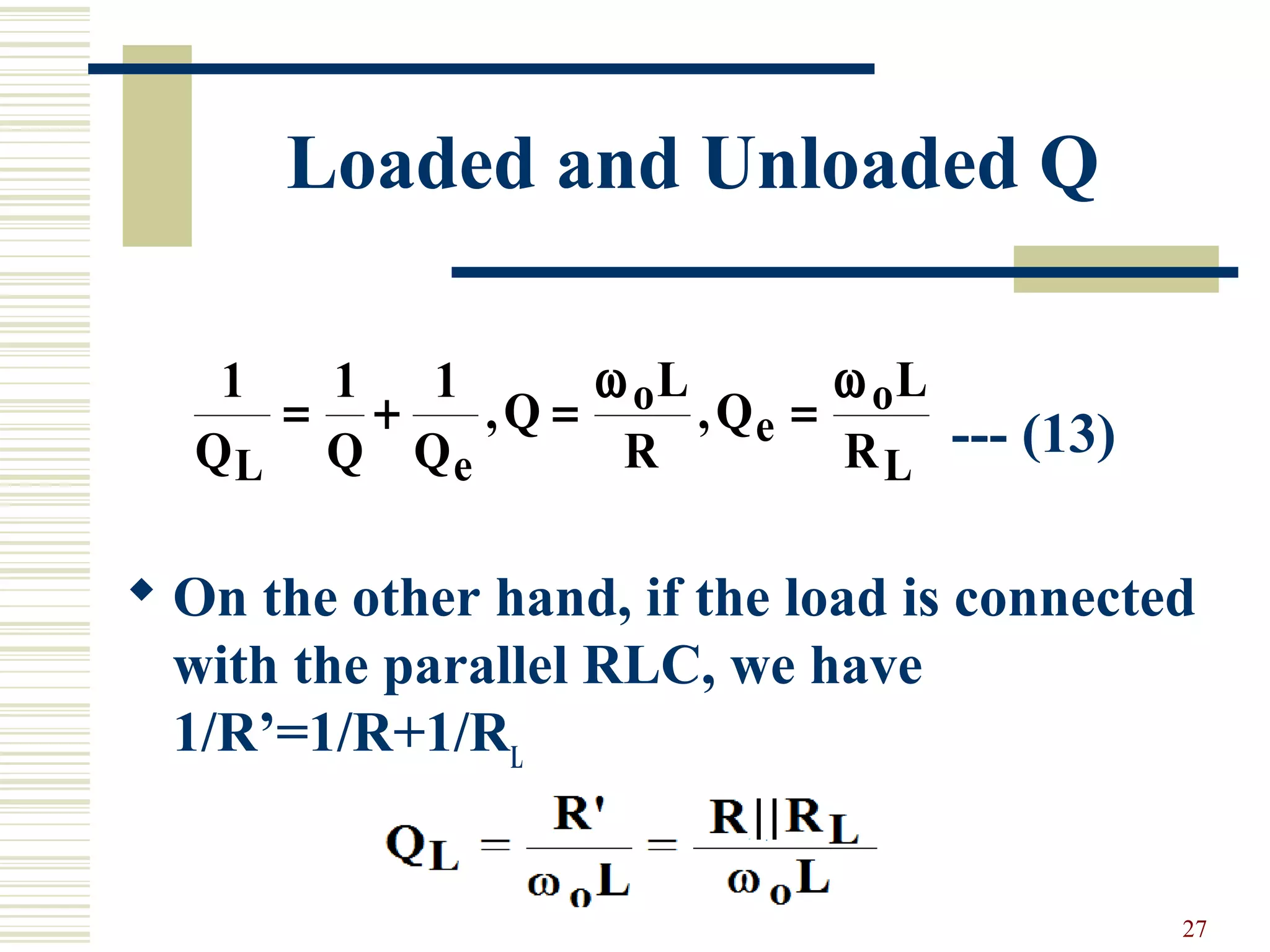
Series and parallel RLC resonator circuits are discussed. A series RLC circuit exhibits resonance at the angular frequency where the average stored magnetic energy equals the average stored electric energy. The quality factor Q of a series RLC circuit increases as the resistance R decreases. For a parallel RLC circuit, Q increases as R increases. Near resonance, the input impedance of both circuits can be approximated using Q and a complex effective frequency accounting for losses. The loaded Q of a resonant circuit decreases when connected to a resistive load.

1. 1
Series and Parallel ResonatorsSeries and Parallel Resonators
Resonators

2. 2
What is a Resonator ?
 A resonator is a device or system that
exhibits resonance or resonant behavior,
i.e., it naturally oscillates at some
frequencies, called its resonant
frequencies, with greater amplitude than
at others.

3. 3
Series RLC Circuits
 Consider the series RLC resonator shown
below:

4. 4
Series RLC Circuits
 The input impedance Zin
is given by
-------(1)
 The average complex power delivered to
the resonator is
Z R j L j
C
in = + −ω
ω
1
P VI Z I I R j L j
C
in in= = = + −






1
2
1
2
1
2
12 2* ω
ω

5. 5
Series RLC Circuits
 The average power dissipated by the
resistor is
 The time-averaged electric energy stored in
the capacitor is
 Similarly, the time-averaged magnetic
energy stored in the inductor is
P I Rloss =
1
2
2
W I Lm =
1
4
2

6. 6
Series RLC Circuits
 Input power can be written as
 The input impedance can then be
expressed as follows:
-----(2)

7. 7
Series RLC Circuits
 At resonance, the average stored magnetic
and electric energies are equal i.e.,
Wm = We.
 So,
 and the resonance frequency is defined as
Z
P
I
Rin
loss= =
2
2/
ωo
LC
=
1

8. 8
Series RLC Circuits
 The Quality factor is defined as the
product of the angular frequency and the
ratio of the average energy stored to
energy loss per second
 Q is a measure of loss of a resonant
circuit.
 Lower loss implies higher Q and high Q
implies narrower bandwidth.
Q
W W
P
m e
loss
=
+
ω

9. 9
Series RLC Circuits
 At resonance We
= Wm
and we have
----
(3)
 When R decreases, Q increases as R
dictates the power loss.
Q
W
P
L
R RC
o
m
loss
o
o
= = =ω
ω
ω
2 1

10. 10
Series RLC Circuits
 The input impedance can be rewritten in
the following form:
Z R j L j
C
R j L
LC
Rin = + − = + − = +ω
ω
ω
ω
1
1
1
2
( )

11. 11
Series RLC Circuits
 and
 so Zin can be written as
---(4)
ω ω ω ω ω ω ω2 2
2− = − + = •o o o( )( ) ∆ω
Z R j L R j L R j
RQ
in
o
≈ + = + = +ω
ω∆ω
ω ω
2
2
2
2
∆ω
∆ω

12. 13
Series RLC Circuits
 Consider the equation
 As
---(5)
Z R j L
L
Q
j Lin
o
o≈ + = + −2 2∆ω
ω
ω ω( )
Q
L
R
o=
ω
Z j L
j Q
j L j
Q
in o
o
o≈ − + = − +2
2
2 1
1
2
( ) [ ( )]ω ω
ω
ω ω

13. 14
Series RLC Circuits
 From the EQ.4, when
R = 0 for the lossless case, therefore, we
can define a complex effective frequency
----(6) so that,
--- (7) to incorporate
the loss
Z j Lin ≈ 2 ∆ω
ω ωo o j
Q
' ( )= +1
1
2
Z j Lin o≈ −2 ( )'
ω ω

14. 15
Series RLC Circuits
 From EQ.4 we have Z R j
RQ
in
o
≈ +
2 ∆ω
ω

15. Series RLC Circuits
16

16. 17
Parallel RLC Circuits
 Now let us turn our attention to the
parallel RLC resonator:

17. 18
Parallel RLC Circuits
 The input impedance is equal to
-----(9)
 At resonance, and ,
same results as we obtained in series RLC
Z
R j L
j Cin = + +






−
1 1
1
ω
ω
Z Rin = ωo
LC
=
1

18. 19
Parallel RLC Circuits
 The quality factor, however, is different
Q
W
P P
I L
I R
I L
Q
L
R
V L
V R
R
L
RC
o
m
loss
o
loss
L
o
R
L
o o
o
o
= = =
= = = − − −
ω ω ω
ω ω
ω
ω
2 2
4
2
2 4
10
2
2
2
2 2
2 2
| |
/
| |
/ ( )
/
( )

19. 20
Parallel RLC Circuits
 Contrary to series RLC, the Q of the
parallel RLC increases as R increases.
 Similar to series RLC, we can derive an
approximate expression of Zin for parallel
RLC near resonance .

20. 21
Parallel RLC Circuits
 Given ∆ω = −ω ωo
Z
R j L
j C
R j L
j C j Cin
o
o= + +





 = +
−
+ +






− −
1 1 1 1
1 1
ω
ω
ω
ω
ω
∆ω
∆ω
/
Z
R
j
L j L
j C j Cin
o o
o= + + + +






−
1 1
1
∆ω
∆ω
ωω ω
ω
Z
R
j
L
LC
j L
j Cin
o
o
o
= + +
−
+








−
1 1 2 1
∆ω
∆ω
ωω
ω
ω

21. 22
Parallel RLC Circuits
----(11)
Z
R
j
L
j Cin
o
o= + +







 ≈
−
1
2
1
∆ω
∆ω
ω
ω ω,
Z
R
j
L LC
j Cin = + +






−
1
1
∆ω
∆ω
/ ( )
Z
R
j Cin = +






−
1
2
1
∆ω
Z
R
j RC
R
j Q
in
o
=
+
=
+1 2 1 2∆ω ∆ω / ω

22. 23
Parallel RLC Circuits
 Similar to the series RLC case, the effect
of the loss can be incorporated into the
lossless result by defining a complex
frequency equal to
-----(12)ω ωo o j
Q
'
( )= +1
1
2

23. Parallel RLC Circuits
24

24. 25
Loaded and Unloaded Q
 Q defined above is a characteristic of the
resonant circuit, this will change when the
circuit is connected to a load
Resonant
circuit Q
R
L

25. 26
Loaded and Unloaded Q
 if the load is connected with the series
RLC, the resistance in the series RLC is
given by R’=R+RL
, the corresponding
quality factor QL
becomes
Q
L
R
L
R R R
L
R
L
L
o o
L
o
L
o
= =
+
=
+
ω ω
ω ω
'
1

26. 27
Loaded and Unloaded Q
--- (13)
 On the other hand, if the load is connected
with the parallel RLC, we have
1/R’=1/R+1/RL
1 1 1
Q Q Q
Q
L
R
Q
L
RL e
o
e
o
L
= + = =, ,
ω ω

27. 28
Loaded and Unloaded Q
1
1 1 1
1
Q
L
R R R L RL
o
L o L
=
+
= +
ω
ω/ ( / / ) / ( )
1 1 1
1 1 1 1L
R R R L R L Q QL
o
L o L o e
=
+
= + = +
ω
ω ω/ ( / / ) / ( ) / ( )
1 1 1 1
R L R L Q Qo L o e
+ = +
ω ω/ ( ) / ( )

28. Series and Parallel Resonators
29

29. 30