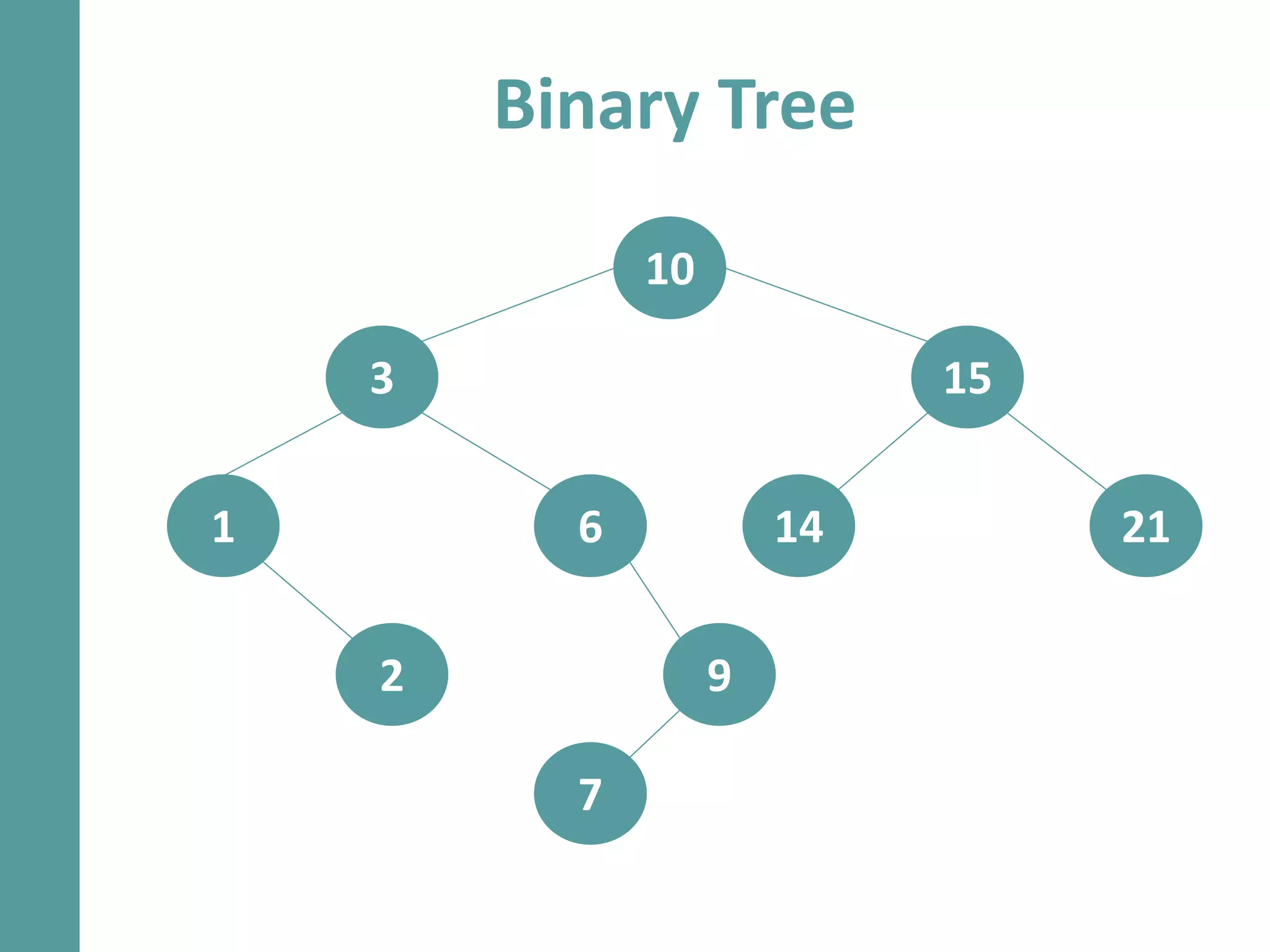
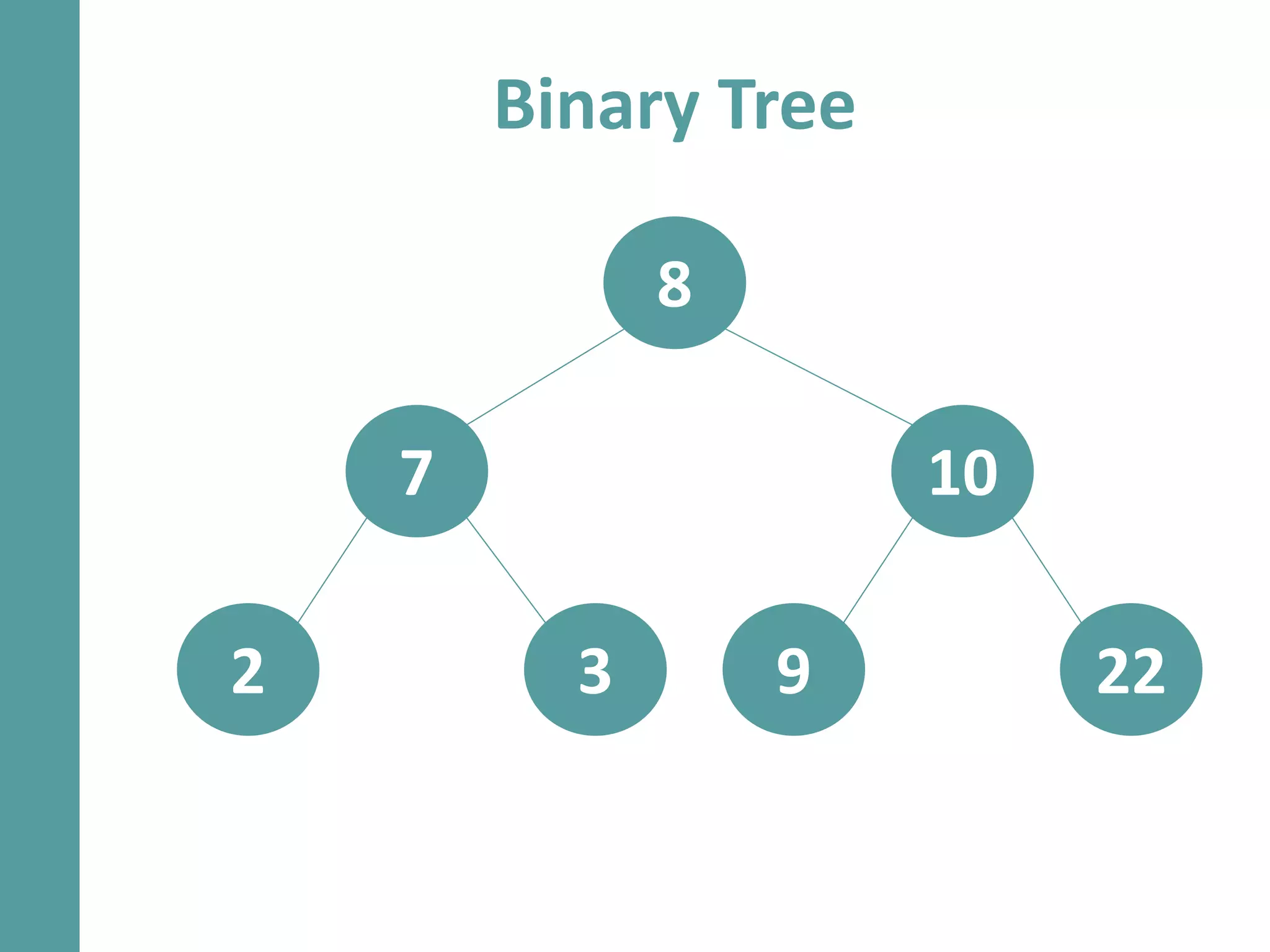
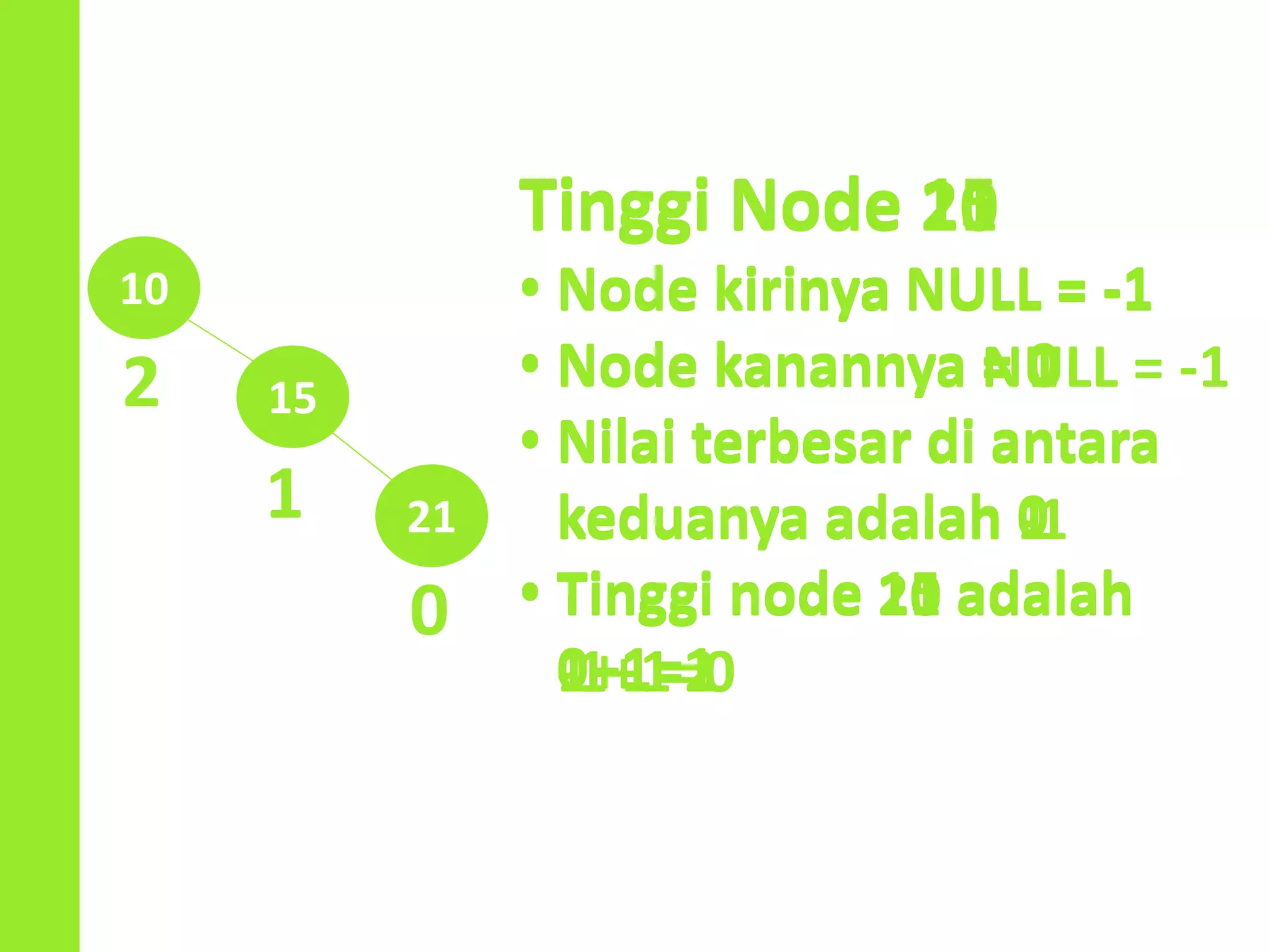
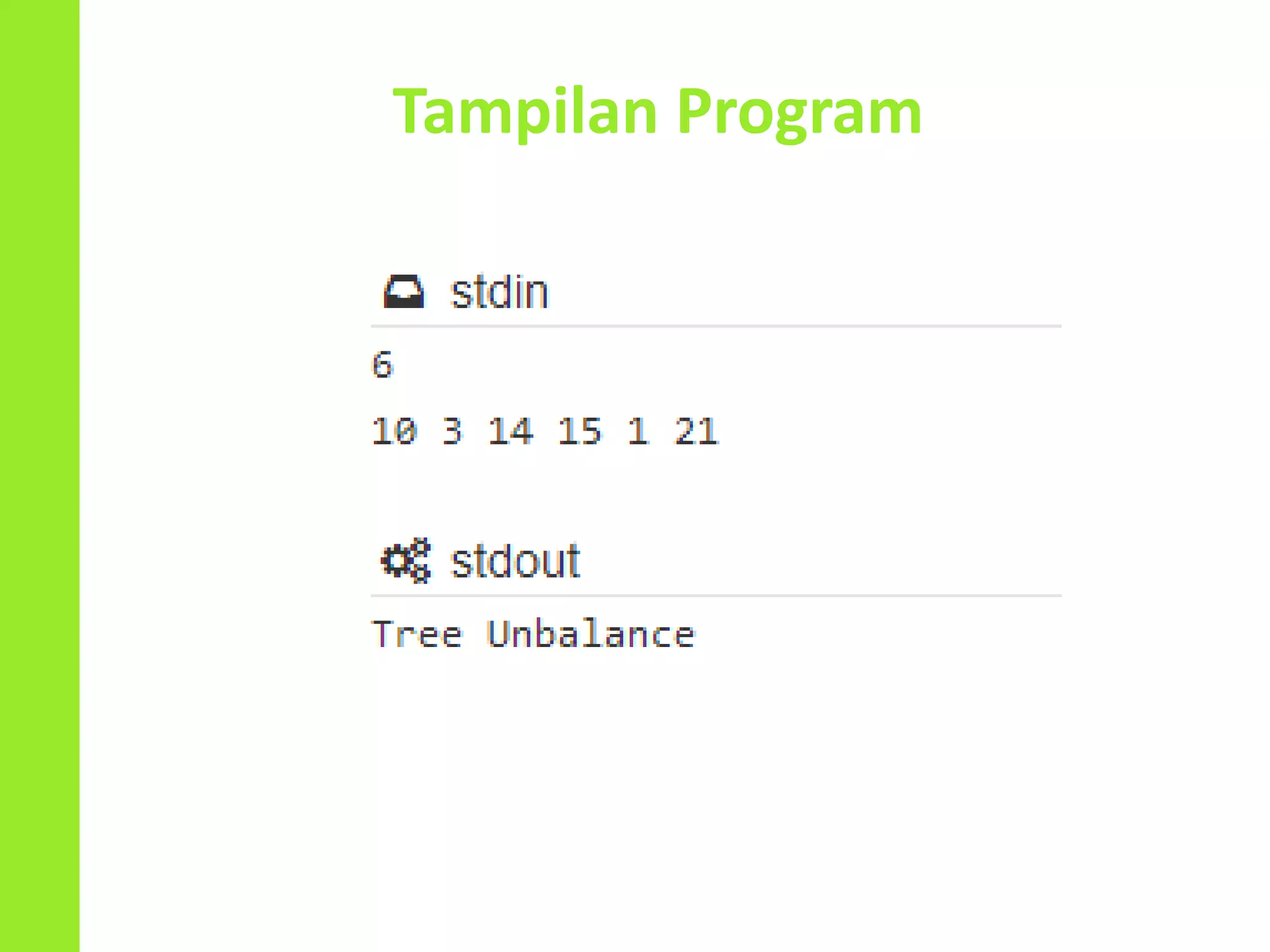
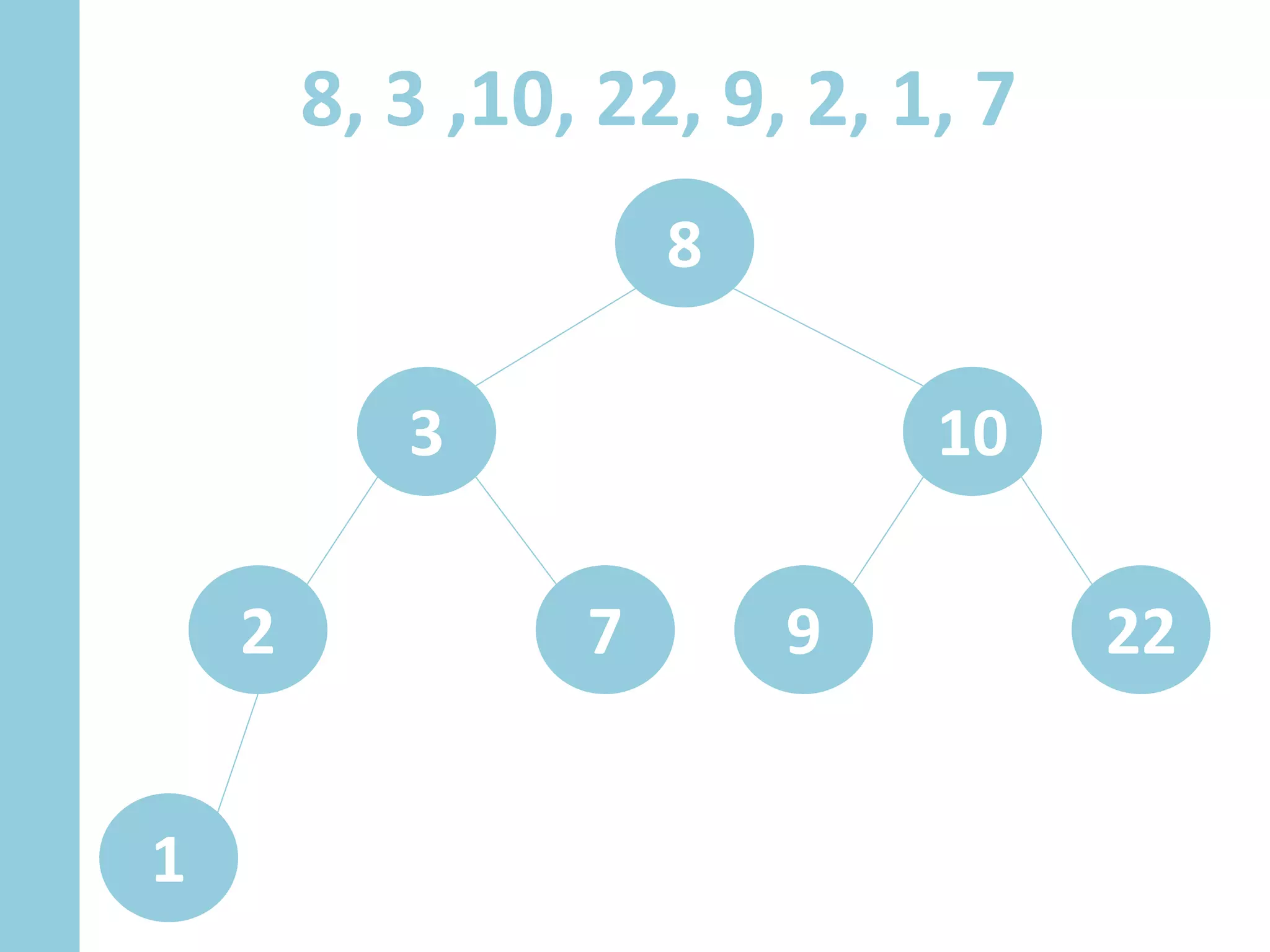
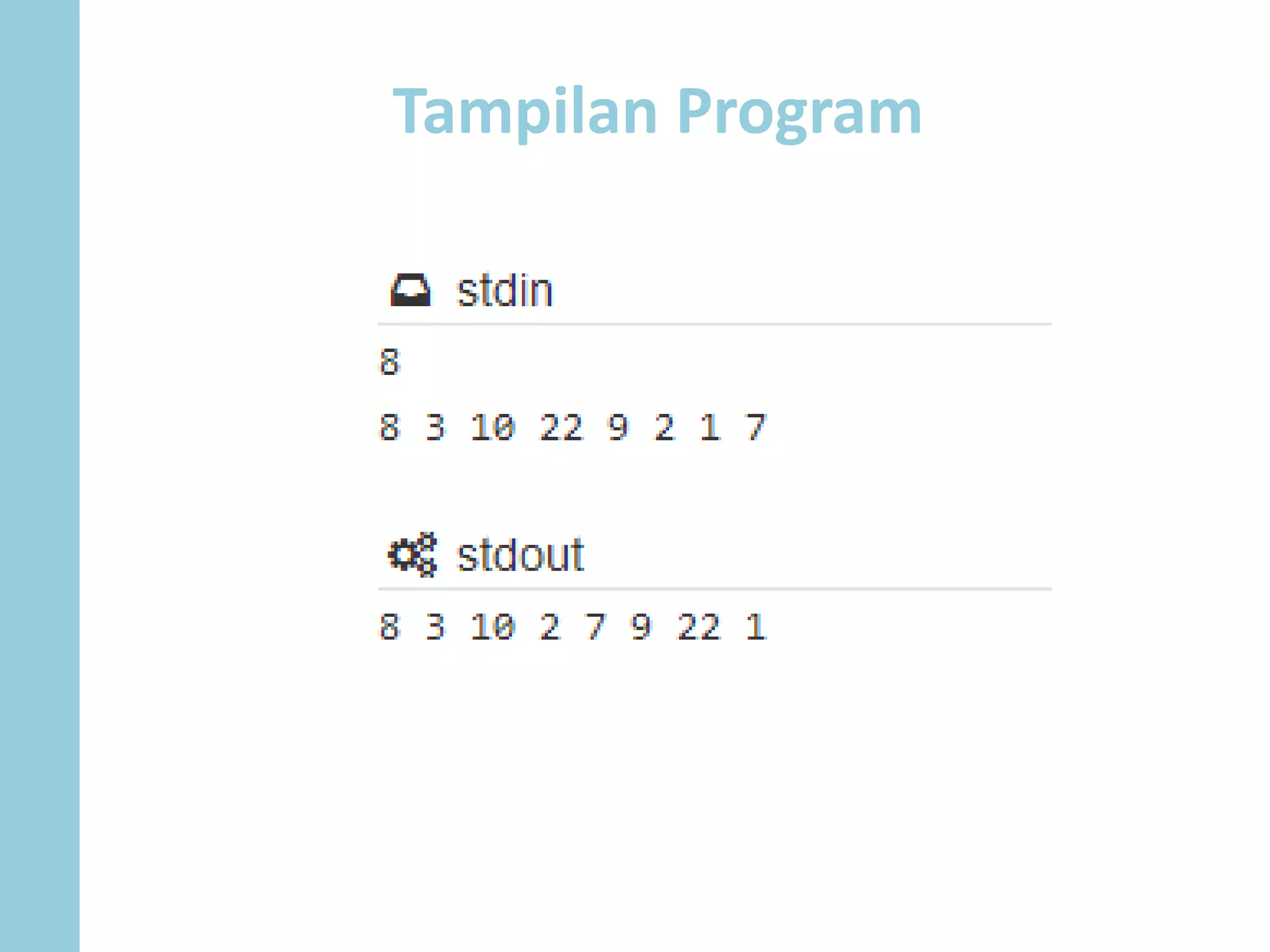
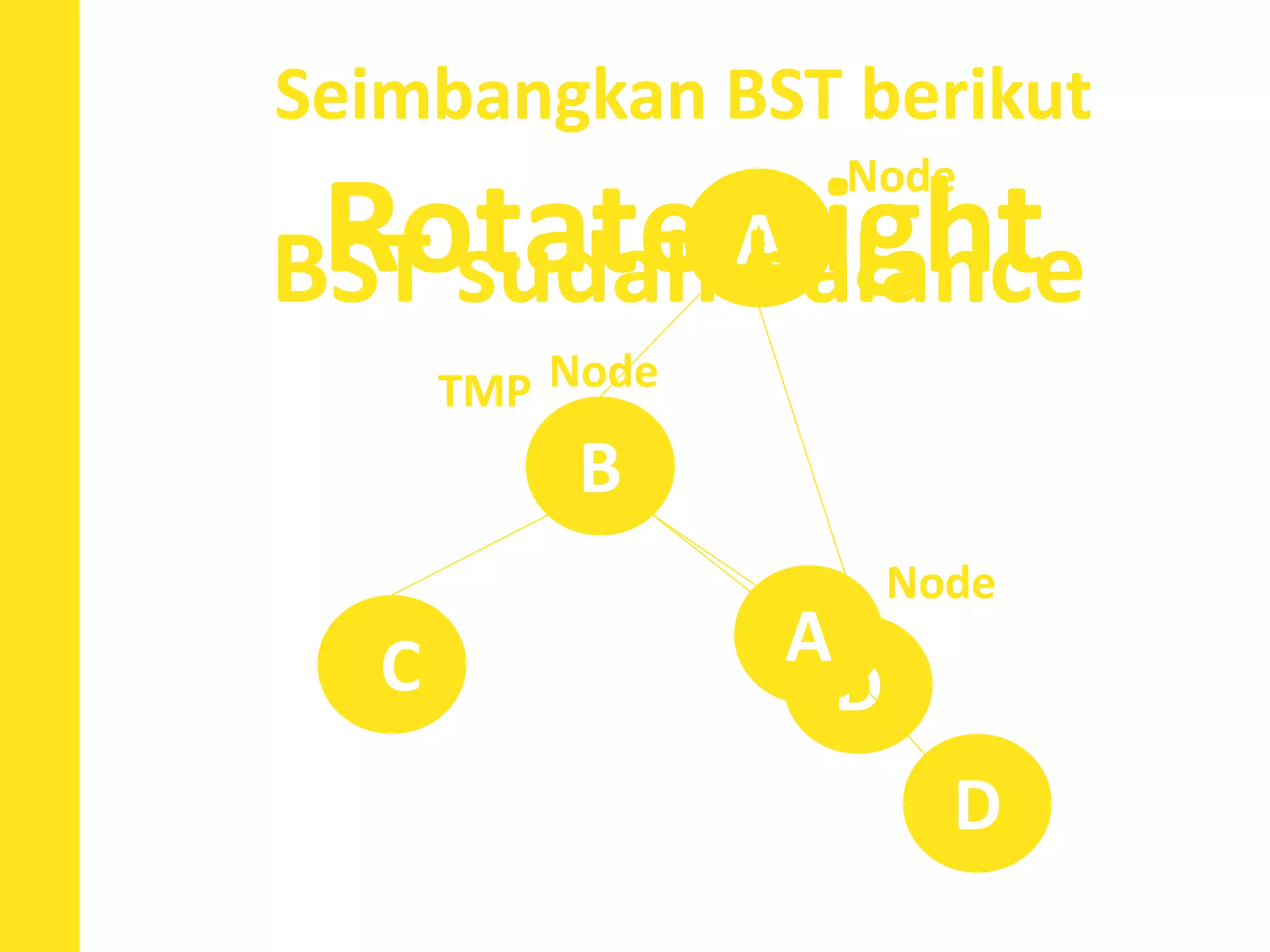
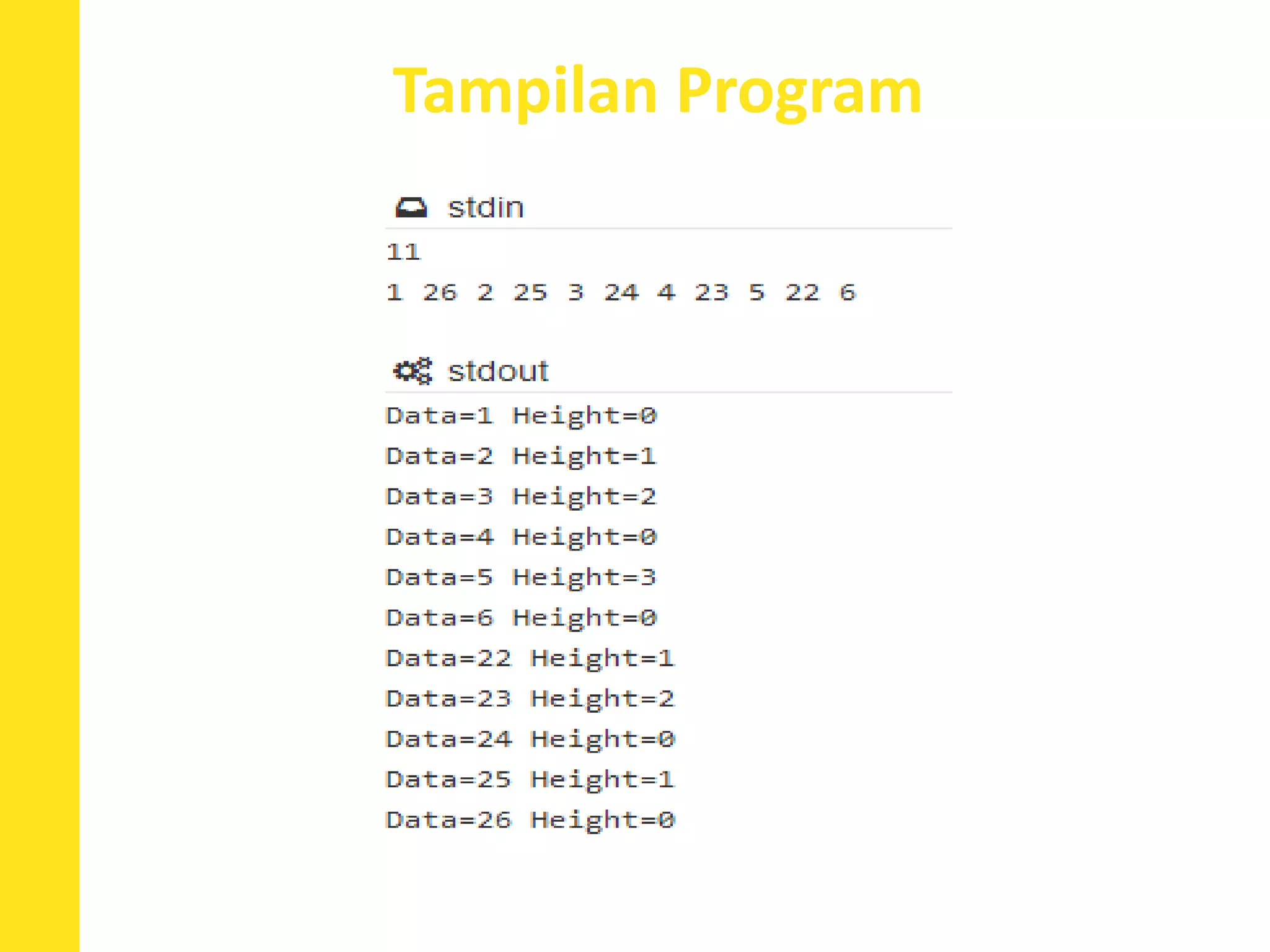
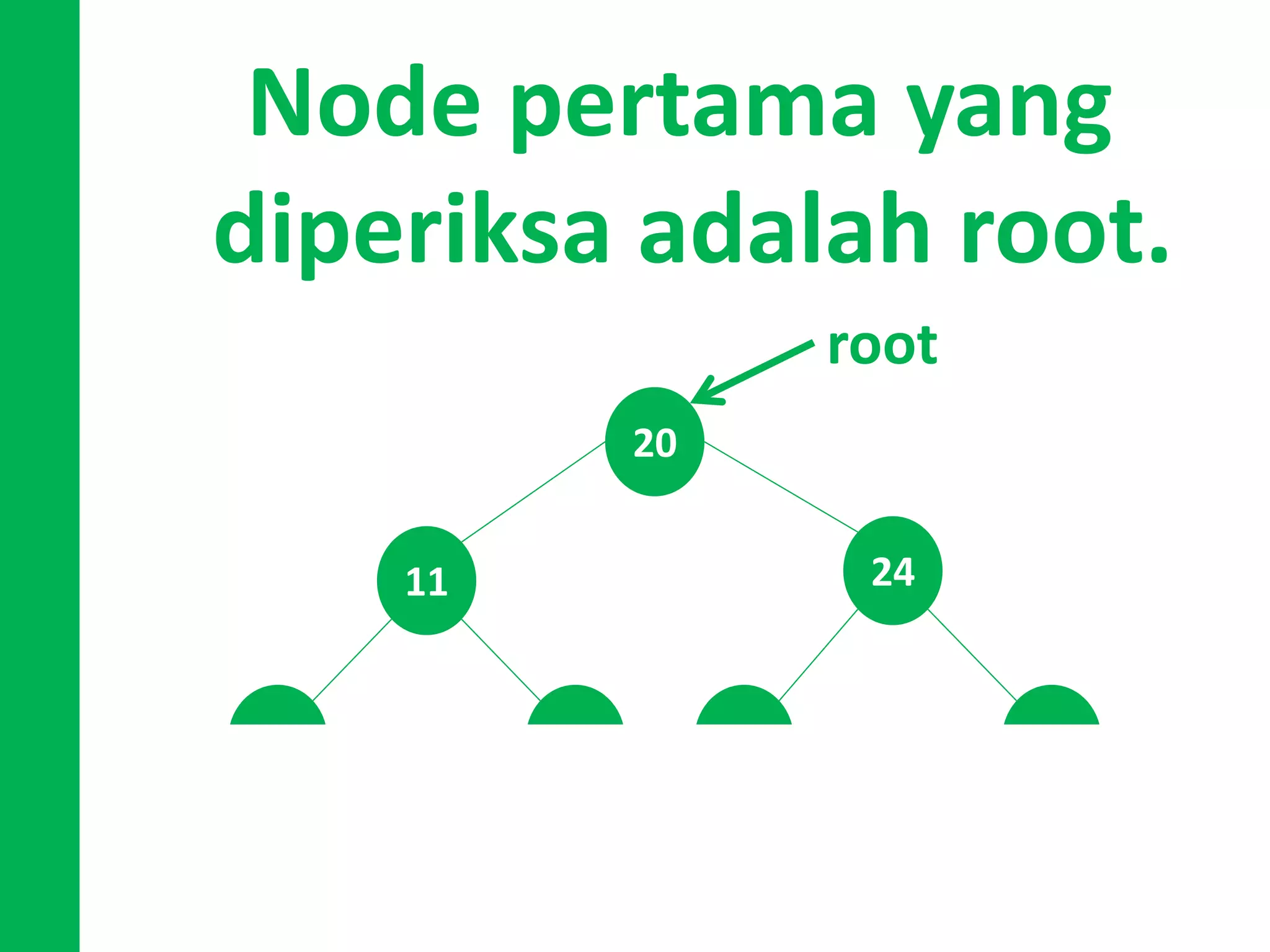
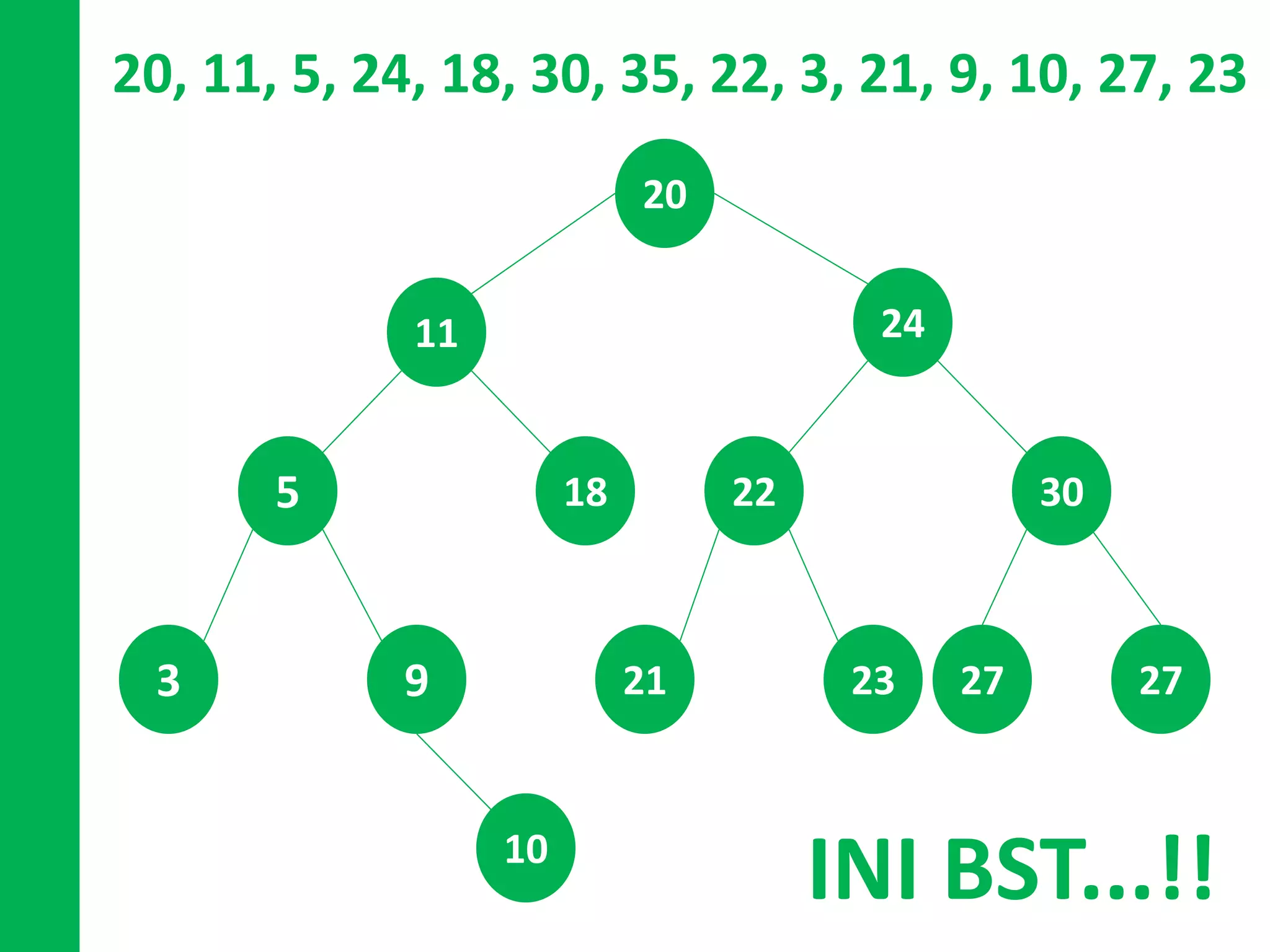
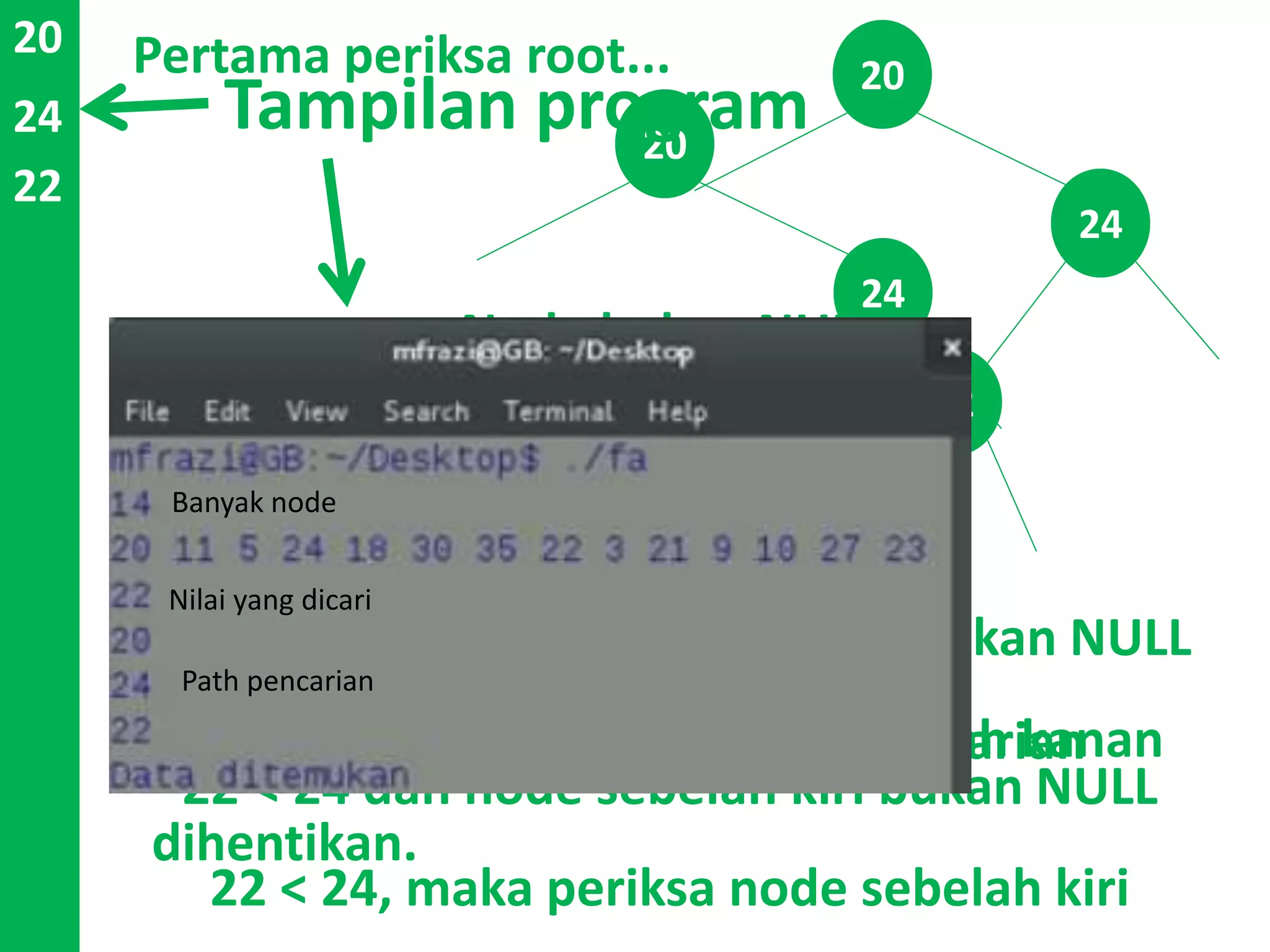
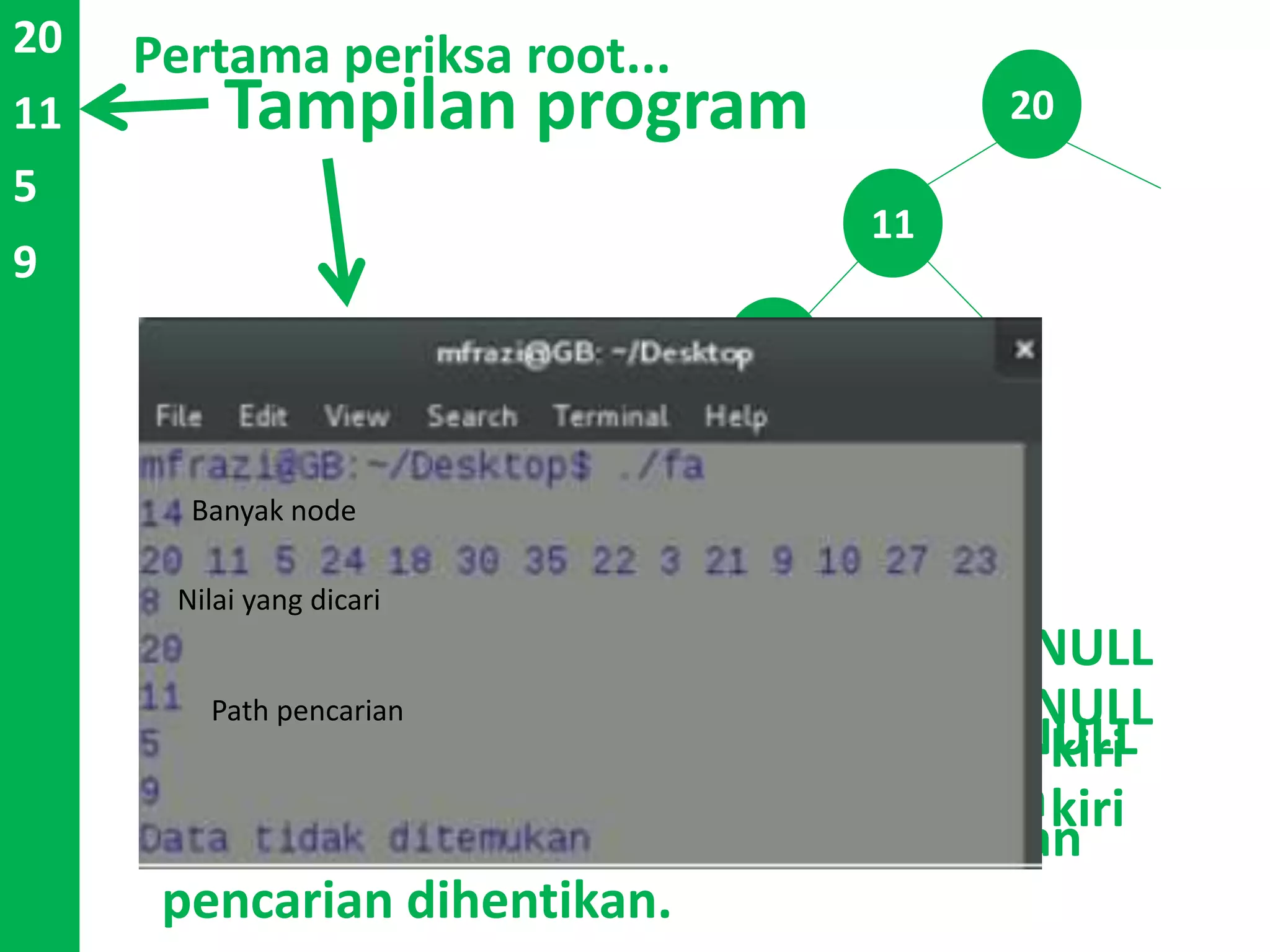
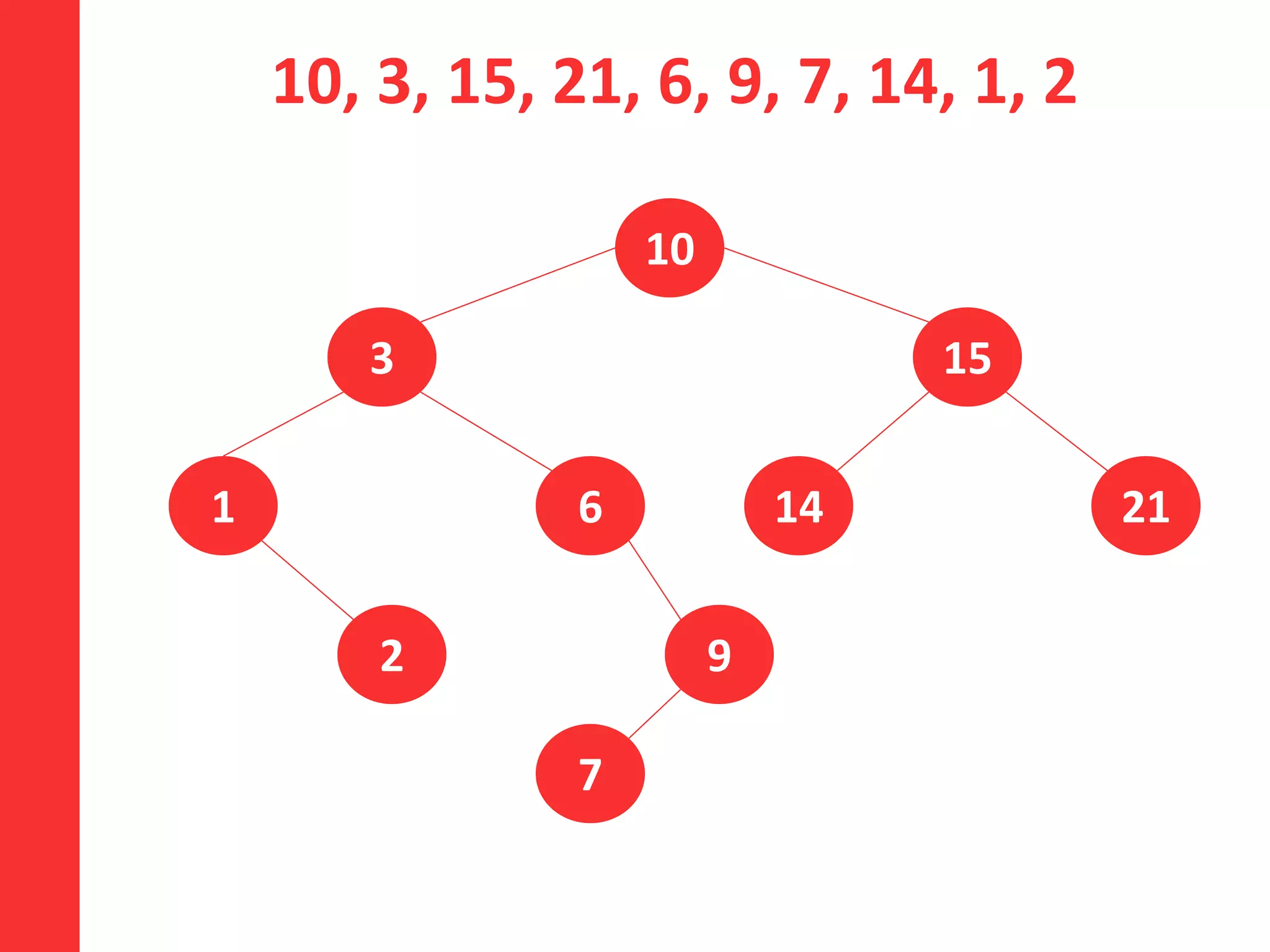
Dokumen ini menjelaskan konsep dan operasi dasar pada binary tree, termasuk pengujian apakah sebuah binary tree adalah binary search tree (BST) dan metode untuk menyeimbangkan BST. Selain itu, dijelaskan juga tentang traversal menggunakan BFS, pencarian nilai dalam BST, dan mencari lowest common ancestor (LCA) antara dua node. Contoh kode dan hasil eksekusi program disertakan untuk ilustrasi lebih lanjut.

1. Binary Tree==BST

2. Untuk mengetahui
apakah sebuah binary
tree adalah BST,
salah satu caranya adalah
dengan melakukan
print in order
BST : Binary Search Tree

3. Print in order, melakukan print
node sebelah kiri, kemudian
induknya, kemudian node
sebelah kanan.m
Jika tampilan tree dalam print in
order terurut dari kecil ke besar,
maka tree tersebut BST, jika tidak
maka tree tersebut bukan BST.

4. 10
3 15
216
9
7
141
2
Binary Tree

5. Apakah
binary tree di
atas adalah
BST ?

6. Lakukan print in order
pada tree di atas
10
3 15
216
9
7
141
2
1
2
3
4
5
6
7
8
9
10
1 2 3 6 7 10 14 15 219
Hasil print in order sudah urut
dari kecil ke besar
Maka binary tree di atas adalah
BST

7. 8
7
2
10
3 9 22
Binary Tree

8. Apakah
binary tree di
atas adalah
BST ?

9. 8
7
2
10
3 9 22
Lakukan print in order
pada tree di atas
1
2
3
4
5
6
7
2 227 3 8 9 10
Hasil print in order tidak urut
dari kecil ke besar
Maka binary tree di atas bukan
BST

10. Tampilan Program

11. BST balance

12. Untuk mengetahui
apakah sebuah BST
balance dapat diketahui
dengan melakukan
pengecekkan tinggi
sebuah node

13. Mencari tinggi
(height)
sebuah node ?

14. Tinggi sebuah node :
Nilai terbesar antara tinggi node
kanan dan tinggi node kiri
ditambah 1.
Jika nodenya adalah NULL, maka
tingginya -1.

15. 10
15
21
Tinggi Node 21
• Node kirinya NULL = -1
• Node kanannya NULL = -1
• Nilai terbesar di antara
keduanya adalah -1
• Tinggi node 21 adalah
-1+1=0
1
0
2
Tinggi Node 15
• Node kirinya NULL = -1
• Node kanannya = 0
• Nilai terbesar di antara
keduanya adalah 0
• Tinggi node 15 adalah
0+1=1
Tinggi Node 10
• Node kirinya NULL = -1
• Node kanannya = 1
• Nilai terbesar di antara
keduanya adalah 1
• Tinggi node 10 adalah
1+1=2

16. BST tidak balance jika:
Ada node yang
tinggi node kirinya
dikurang
tinggi node kanannya
tidak sama dengan
-1, 0, 1

17. 10
3
15
21
14
1
-1-(-1)=0
-1-(0)=-1
-1-(1)=-2
-1-(-1)=0
1-2=-1
0-(-1)=1
Apakah BST berikut balance?
10, 3, 14, 15, 1, 21
Ada node yang tinggi kiri
dikurang tinggi kanannya
tidak sama dengan -1, 0 , 1.
Berarti BST ini tidak balance.

18. Tampilan Program

19. Apakah BST berikut balance?
8, 3 ,10, 22, 9, 2, 1, 7
8
3
2
1
10
7 9 22
-1-(-1)=0-1-(-1)=0-1-(-1)=0
-1-(-1)=0
0-0=0
0-(-1)=1
1-0=1
2-1=1
Tidak ada node yang
tinggi kirinya dikurang tinggi kanannya
di luar dari -1, 0 , 1.
Berarti BST ini balance.

20. Tampilan Program

21. Tree traversal BFS,
gunakan queue

22. Tree traversal dengan BFS
artinya menampilkan
semua isi node
Level 0  Level n-1
BFS : Breadth-first search

23. Langkah-langkah
tree traversal dengan
BFS
dengan bantuan
queue

24. •Inisialisasi isi node pertama queue dengan
root (front).
•Ulang selama queue tidak kosong.
oJika node (front) sebelah kiri tidak kosong,
masukkan datanya ke dalam queue.
oJika node (front) sebelah kanan tidak
kosong, masukkan datanya ke dalam queue.
oDequeue dan tampilkan node front.

25. 8, 3 ,10, 22, 9, 2, 1, 7
8
3
2
1
10
7 9 22

26. Lakukan tree
traversal pada
tree di atas

27. 32 1078 10
Isi queue dengan
root
8
Karena queue tidak kosong, maka :
Node sebelah kiri 8 tidak kosong, masukkan
queue
Node sebelah kanan 8 tidak kosong,
masukkan queue
Keluarkan dan tampilkan 8
8
3 10
8
3
2 7
72
Karena queue tidak kosong, maka :
Node sebelah kiri 3 tidak kosong, masukkan
queue
Node sebelah kanan 3 tidak kosong,
masukkan queue
Keluarkan dan tampilkan 3
3
10
9 22
Karena queue tidak kosong, maka :
Node sebelah kiri 10 tidak kosong, masukkan
queue
Node sebelah kanan 10 tidak kosong,
masukkan queue
Keluarkan dan tampilkan 10
9 2210
9 22
2
1
Karena queue tidak kosong, maka :
Node sebelah kiri 2 tidak kosong, masukkan
queue
Node sebelah kanan 2 kosong
Keluarkan dan tampilkan 2
1
2
Karena queue tidak kosong, maka :
Node sebelah kiri 7 kosong
Node sebelah kanan 7 kosong
Keluarkan dan tampilkan 7
7
7
9
Karena queue tidak kosong, maka :
Node sebelah kiri 9 kosong
Node sebelah kanan 9 kosong
Keluarkan dan tampilkan 9
9
22
Karena queue tidak kosong, maka :
Node sebelah kiri 22 kosong
Node sebelah kanan 22 kosong
Keluarkan dan tampilkan 22
22
1
Karena queue tidak kosong, maka :
Node sebelah kiri 1 kosong
Node sebelah kanan 1 kosong
Keluarkan dan tampilkan 1
1
Queue sudah kosong, maka proses traversal sudah selesai
Tampilan program
3

28. Tampilan Program

29. AVL Tree
1, 26, 2, 25, 3, 24, 4, 23, 5, 22, 6

30. AVL tree adalah
tree yang
balance
Bagaimana tree yang balance?

31. Setiap kali menginputkan
sebuah node baru, kita
akan periksa apakah
treenya sudah balance
atau belum,
Jika belum, maka :

32. Ada empat cara untuk
menyeimbangkan sebuah tree:
1.Rotate Left
2.Rotate Right
3.Rotate Right Left
4.Rotate Left Right

33. A
B
DC
Node
TMP
A
C
Node
Node
Seimbangkan BST berikut
Rotate LeftBST sudah balance

34. Seimbangkan BST berikut
Rotate Right
B
D
A
C
Node
TMP
D
A
Node
Node
BST sudah balance

35. 1
26
2
25
3
24
4
23
5
22
6 Rotate Right LeftRotate Right
1
26
2
2
261
25
3
2
251
3 26
24
2 25
1
3
2624
4
23
Rotate Left Right
2 25
1
3
2623
4 24
5
2 23
1
3
254
5 2624
22
Rotate Left
2 23
1
3
255
4 262422
6
2
23
1
3
25
5
4
2624
22
6
Semua input sudah dimasukkan.
Tree di atas adalah hasilnya, berupa
AVL tree dan tentunya sudah balance

36. Tampilan Program

37. Path pencarian nilai
suatu BST

38. Langkah-langkah
mencari suatu nilai
pada BST dan
menampilkan path
pencariannya

39. • Tampilkan node yang diperiksa
• Jika nilai node sama dengan X, X ditemukan. Kalau
tidak,
• Jika nilai node lebih besar dari X dan node di
sebelah kiri adalah NULL, atau
Jika nilai node lebih kecil dari X dan node di sebelah
kanan adalah NULL, maka X tidak ditemukan, kalau
tidak,
• Jika nilai node lebih besar dari X, periksa node di
sebelah kiri. Kalau tidak,
• Jika nilai node lebih kecil dari X, periksa node di
sebelah kanan.
Sebut saja nilai yang dicari
adalah X

40. Node pertama yang
diperiksa adalah root.
20
11 24
5 18 22 30
root

41. 20
11 24
5 18 22 30
3 9 21 23 27 27
10
20, 11, 5, 24, 18, 30, 35, 22, 3, 21, 9, 10, 27, 23
INI BST...!!

42. Cari angka
22
dari BST di atas

43. 20
Node bukan NULL
Tampilkan nilai node
22 != 20
22 > 20 dan node sebelah kanan bukan NULL
22 > 20, maka periksa node sebelah kanan
20
24
Node bukan NULL
Tampilkan nilai node
22 != 24
22 < 24 dan node sebelah kiri bukan NULL
22 < 24, maka periksa node sebelah kiri
24
20
24
Pertama periksa root...
22
Node bukan NULL
Tampilkan nilai node
22 == 24, nilai ditemukan dan pencarian
dihentikan.
22
Tampilan program
Banyak node
Nilai yang dicari
Path pencarian

44. Cari angka
8
dari BST di atas

45. Node bukan NULL
Tampilkan nilai node
8 != 9
8 < 9 dan node sebelah kiri NULL,
maka nilai tidak dapat ditemukan dan
pencarian dihentikan.
Node bukan NULL
Tampilkan nilai node
8 != 5
8 > 5 dan node sebelah kanan bukan NULL
8 > 5, maka periksa node sebelah kanan
20
Pertama periksa root...
Node bukan NULL
Tampilkan nilai node
8 != 20
8 < 20 dan node sebelah kiri bukan NULL
8 < 20, maka periksa node sebelah kiri
20
11
Node bukan NULL
Tampilkan nilai node
8 != 11
8 < 11 dan node sebelah kiri bukan NULL
8 < 11, maka periksa node sebelah kiri
11
5
5
9
9
Tampilan program
Banyak node
Nilai yang dicari
Path pencarian

46. Langkah di atas hanya bisa dilakuakan jika :
•Tree yang digunakan
adalah BST
•Tidak ada dua nilai atau
lebih yang sama di
dalam tree

47. LCA pada BST

48. Lowest Common Ancestor (LCA)
Let T be a rooted tree with n
nodes. The lowest common
ancestor between two nodes v
and w is defined as the lowest
node in T that has both v and w
as descendants (where we allow
a node to be a descendant of
itself).

49. •Node yang pertama diperiksa adalah root
•Jika :
oa ≤ isi node dan b > isi node, atau
ob ≤ isi node dan a > isi node, atau
oa == isi node dan b < isi node, atau
ob == isi node dan a < isi node
Tampilkan isi node
•Kalau tidak, jika:
oa < isi node dan b < isi node
Periksa node sebelah kiri
•Kalau tidak, jika:
oa > isi node dan b > isi node
Periksa node sebelah kanan

50. 10, 3, 15, 21, 6, 9, 7, 14, 1, 2
10
3 15
216
9
7
141
2

51. Cari LCA dari
1 dan 14

52. Periksa root
10
1 lebih kecil dari 10 dan 14 lebih
besar dari 10
Maka LCA dari 1 dan 14 adalah 10

53. Cari LCA dari
3 dan 9

54. Periksa root
10
9 lebih kecil dari 10 dan 3 lebih kecil
dari 10
Maka periksa node sebelah kiri
3
9 lebih besar dari 3 dan 3 sama
dengan 3 (node yang dicari)
Maka LCA dari 3 dan 9 adalah 3

55. Tampilan Program

56. Cara di atas hanya dapat digunakan jika :
• Tree yang digunakan adalah
BST
• Tidak ada dua buah atau lebih
isi node yang sama
• Dua buah node yang di cari
LCAnya harus ada di dalam
tree

57. Reference :
Mark Allen Weiss, “AVL Tree”, Data Structures
& Algorithm Analysis in C++, (2) 1999, 143-
155
Source Code :
https://www.dropbox.com/sh/7b6m3j7v3semk8
y/s987IXfj4j/SC

58. Oleh
Muhammad Fahrul Razi
5113100105
Teknik Informatika
Institut Teknologi Sepuluh November