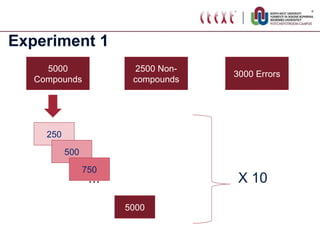
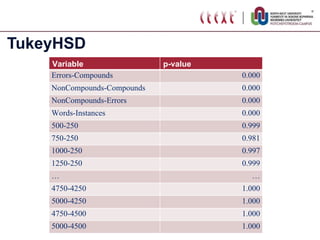
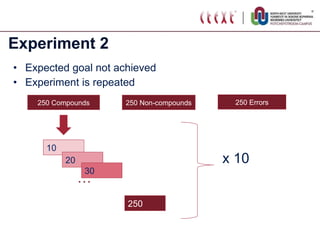
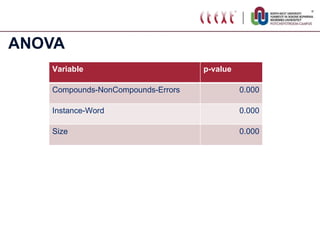
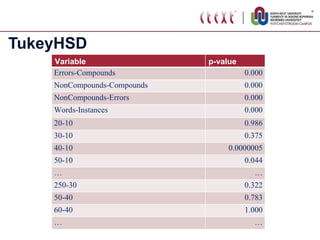
The document proposes standardizing test sets for evaluating compound analyzers by establishing parameters for a standard test set. It discusses evaluating compound analyzers on different sized test sets containing compound words, non-compound words, and error words. Experiments compare analyzer performance on test sets of varying sizes, finding sizes below 250 words are too small and sizes above 1250 words show no significant differences in results. The proposed standard test set consists of 500 examples each of compounds, non-compounds, and errors for a total of 1500 words.

1. Towards Standardizing Evaluation Test Sets for Compound Analysers

2. Contents Introduction Related work Evaluation of compound analysers Parameter of standard test sets Metrics for evaluation Experimental set-up Data Experiments Results and discussion Conclusion

3. Introduction Importance of compound analysers Compounding is productive process Evaluations of compound analysers differ Results cannot be compared Propose to standardize: Test set Set of metrics Standardization will enable comparison Problem: no standard test set

4. Evaluation of Compound Analysers Test set contains test data Used to test compound analyser Change outcome of evaluation Representative of task Ensure reliability and validity

5. Parameters of Standard Test Sets Ensure set can be rebuilt Include total number of data types Represent properties of language Well-balanced test set

6. Parameters of Standard Test Sets II Size is most important Assume that larger test set = stable results El-Emam (2000) Results will normalize Minimum size is where results normalize Optimum test set: Set with results not statistically significantly different

7. Metrics for Evaluation There are three commonly used metrics: Accuracy Schiller (2006) Error rate Van Huyssteen & Van Zaanen (2004) Precision, Recall and F-score Pilon et al. (2008)

8. Data Categories Focus: determine what a standard test set looks like Test set has three different categories of data: Compound words Non-compound words Error words: Real-world errors Generated errors

9. Compound Words sjokoladekoek (chocolate cake)

10. Compound Words II sjokoladekoek sjokolade + koek (chocolate cake) (chocolate) + (cake)

11. Non-compound Words balkonnetjie ( balcony + DIM )

12. Non-compound Words II balkonnetjie bal + kon + netjie ( balcony + DIM )

13. Error Words Real-world errors: aanbeve e lingsbrief (letter of recommendation) Generated errors: prok k ureur (lawyer) bakkersl u sensie (baker’s license) gebr uk ersnaam (username)

14. Error Words II Real-world errors: aanbeve e lingsbrief aanbeve e ling _ s + brief (letter of recommendation) (recommendation) + (letter) Generated errors: prok k ureur prok k ureur (lawyer) bakkersl u sensie bakker _ s + l u sensie (baker’s license) (baker) + (license) gebr uk ersnaam gebr uk er _ s + naam (username) (user) + (name)

15. Experiments TiMBL is used Wordlists obtained from CKARMA Van Huyssteen et al. (2005) Words extracted for test purposes: 5,000 compounds 2,500 non-compounds Two lists combined into training set Errors file has 3,000 words: 2,113 real-world errors 887 generated errors Substitution used to generate errors Search for assosiasie (association) Create a s osiasiegrond (association ground)

16. Experiment 1 ... X 10 5000 Compounds 2500 Non-compounds 3000 Errors 250 500 5000 750

17. Instance and Word Level Evaluation results calculated on two levels: Instance level Word level For example: Consider the word stoelpoot (chair leg) s + t + o + e + l + p + o + o + t (c + h + a + i + r l + e + g) stoel + poot (chair leg)

18. Results and Discussion Results compared for statistical significance The null hypothesis, H 0 , of the experiment is: The performance of a smaller set cannot be shown to be significantly different compared to that of a larger set. F-test determines significant difference P-value determines if result significantly different ANOVA and TukeyHSD summarize results Determine significant difference between: Data types (compounds, non-compounds and errors) Instance and word level Different sizes

19. ANOVA Variable p-value Compounds-NonCompounds-Errors 0.000 Instance-Word 0.000 Size 0.991

20. TukeyHSD Variable p-value Errors-Compounds 0.000 NonCompounds-Compounds 0.000 NonCompounds-Errors 0.000 Words-Instances 0.000 500-250 0.999 750-250 0.981 1000-250 0.997 1250-250 0.999 … … 4750-4250 1.000 5000-4250 1.000 4750-4500 1.000 5000-4500 1.000

21. Experiment 2 Expected goal not achieved Experiment is repeated x 10 … 250 Compounds 250 Non-compounds 250 Errors 10 20 250 30

22. ANOVA Variable p-value Compounds-NonCompounds-Errors 0.000 Instance-Word 0.000 Size 0.000

23. TukeyHSD Variable p-value Errors-Compounds 0.000 NonCompounds-Compounds 0.000 NonCompounds-Errors 0.000 Words-Instances 0.000 20-10 0.986 30-10 0.375 40-10 0.0000005 50-10 0.044 … … 250-30 0.322 50-40 0.783 60-40 1.000 … …

24. Conclusion Minimum number of words is 250 Minimum size incremented by 250 for reliability Standard test set consists of: 500 compounds 500 non-compounds 500 errors Standard test set has 1500 words Standard test set goal is achieved Should be representative Each data category should have enough examples

25. Future Work Test set not fully evaluated Therefore, we need to compare: Evaluation metrics Settings for algorithm Algorithms Training sets Languages Results should remain statistically similar

26. Thank you!