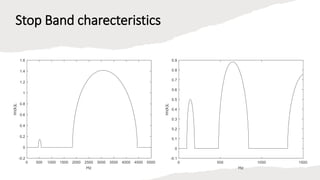
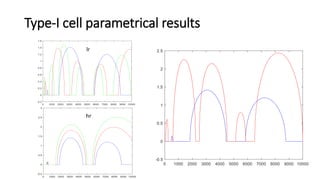
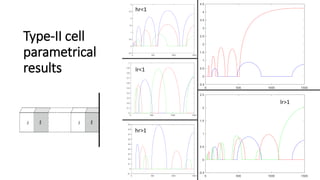
This document discusses the time domain spectral element-based wave finite element method for analyzing periodic Timoshenko beams, which are defined by repetitive unit cells. It highlights the significance of stop bands in periodic structures that result from destructive interference, motivating research into vibration attenuation. Various analysis methods, especially the transfer matrix method and spectral element method, are compared, noting the computational efficiency of the latter over conventional finite element methods.

1. Time domain spectral
element-based wave finite
element method for
periodic Timoshenko Beam
M.E. IN CIVIL ENGINEERING
ROHAN DAS
ROLL NO: 002210402001
SESSION-2022-24

2. Periodic Structure
• A periodic structure can be defined as a structure or material which is formed by repetition
of an identical representative element named a unit cell
• The repetition can be in the form of material properties, boundary conditions, geometry, etc.
• In periodic structures, the stop bands are generated as a consequence of destructive
interference between the incident wave and the reflecting wave due to the change in
geometry or material properties
• The stop bands are the main points of interest of periodic structures which motivates the
research on the use of periodic structures for vibration attenuation.
• The behavior of the whole structure can be analyzed by performing an analysis of a unit cell
which is the main motivation of periodic analysis. The periodic analysis is independent of the
domain and number of unit cells.
Schematic of the periodic unit cell (not
to scale) of the 1-D perodic
Timoshenko beam made of two
different material

3. Method of Analysis
• The methods are plane wave expansion
method (PWE), extended plane wave
expansion method,(EPWE), finite difference
time domain method (FDTD), finite element
method, spectral element method (SEM),
and wave finite element method
• Among all the methods mentioned above, the
transfer matrix method (TMM) is very popular for
analyzing periodic structures
• In SEM, the dynamic stiffness matrix is formed, and
the dynamic response of the structure is expressed
using spectral representations
• Compared to conventional finite element, SEM
reduces the computational cost substantially.

4. Wave finite
element
• Bloch’s theorem was developed
to study the electron behavior in
crystalline solids. Later, it was
adapted to study the elastic wave
propagation in periodic structures.
• For periodic analysis, it is
sufficient to analyze a single cell
which is capable of predicting
thewave propagation
characteristics of the whole
structure.

5. Cells and Periodic
representations…

6. Stop Band charecteristics

7. Type-I cell parametrical results
hr
lr

8. Type-II cell
parametrical
results lr<1
hr<1
hr>1
lr>1

9. THANK YOU !