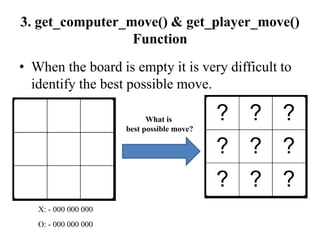
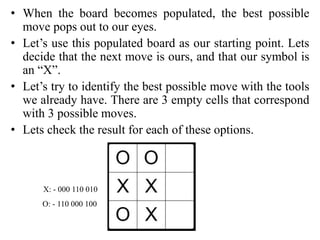
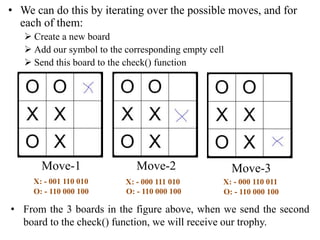
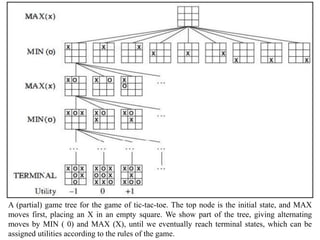
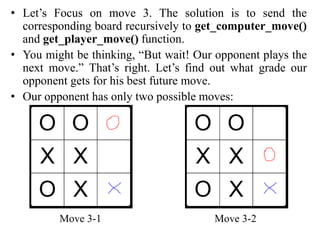
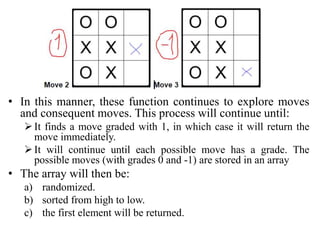
- Tic-tac-toe is a paper-and-pencil game where two players alternate placing Xs and Os on a 3x3 grid. The first player to get 3 in a row wins. - The game uses a 3x3 character matrix to represent the board, and functions like check() to evaluate the board state after each move. - The get_computer_move() function uses minimax search to evaluate all possible future moves and choose the move that maximizes the computer's chance of winning or drawing. It simulates both players' optimal play to assign each possible current move a grade.

2. Tic Tac Toe Game
• Tic-tac-toe (also known as noughts and
crosses or Xs and Os) is a paper-and-pencil
game for two players, X and O, who take turns
marking the spaces in a 3×3 grid.
• The player who succeeds in placing three of their
marks in a horizontal, vertical, or diagonal row
wins the game.
• Players soon discover that the best play from both
parties leads to a draw.
• Hence, tic-tac-toe is most often played by young
children.

3. Data members and functions used
• char matrix[3][3]; //intitial matrix declaration
• char check(void); // checks for someone to win
• void init_matrix(void); //initializes 3*3 matrics
• void get_player_move(void); //get player’s move
• void get_computer_move(void); //get computer’s
move using AI
• void disp_matrix(void); // display matrics after
each move

4. 1. board data structure
• The board matrix (3*3) contains 3 arrays, each
representing a row.
• Each row array contains 3 character or string
elements.
• These elements are either:
– “ ” as an empty string, representing an empty cell
– “X” representing the X player
– “O” representing the O player or computer as a
player

5. 2. check() function
• At any given state, the board will be in one and
one only of these possible states:
– Incomplete
– Player X won
– Player O won(or computer Won)
– or a tie
• The check() function receives a board array,
iterates over all the rows, through all the columns
and across both diagonals.
• It checks the succession of symbols.
• Then it lets us know the current state of that
board.

6. 3. get_computer_move() & get_player_move()
Function
• When the board is empty it is very difficult to
identify the best possible move.
What is
best possible move?
X: - 000 000 000
O: - 000 000 000

7. • When the board becomes populated, the best possible
move pops out to our eyes.
• Let’s use this populated board as our starting point. Lets
decide that the next move is ours, and that our symbol is
an “X”.
• Let’s try to identify the best possible move with the tools
we already have. There are 3 empty cells that correspond
with 3 possible moves.
• Lets check the result for each of these options.
X: - 000 110 010
O: - 110 000 100

8. • From the 3 boards in the figure above, when we send the second
board to the check() function, we will receive our trophy.
Move-1 Move-2 Move-3
• We can do this by iterating over the possible moves, and for
each of them:
 Create a new board
 Add our symbol to the corresponding empty cell
 Send this board to the check() function
X: - 001 110 010
O: - 110 000 100
X: - 000 111 010 X: - 000 110 011
O: - 110 000 100 O: - 110 000 100

9. Please concentrate for the next essential steps:
1. We need to grade the possible moves so we can
compare them. Let’s decide that if a move yields a
winning board we will grade it 1. If it yields a losing
board it will receive the grade of -1. A tie will receive
a grade of 0.
2. Move 2 will receive a grade of 1. When we find a
move graded with 1 we can ignore all other possible
moves. There is no other better possible move than a
definite victory.
3. But for the sake of understanding, how would we
grade moves 1 or 3, or any other move with an
incomplete result?

10. A (partial) game tree for the game of tic-tac-toe. The top node is the initial state, and MAX
moves first, placing an X in an empty square. We show part of the tree, giving alternating
moves by MIN ( 0) and MAX (X), until we eventually reach terminal states, which can be
assigned utilities according to the rules of the game.

11. • Let’s Focus on move 3. The solution is to send the
corresponding board recursively to get_computer_move()
and get_player_move() function.
• You might be thinking, “But wait! Our opponent plays the
next move.” That’s right. Let’s find out what grade our
opponent gets for his best future move.
• Our opponent has only two possible moves:
Move 3-1 Move 3-2

12. • Move 3–1 will win the game in favor of our
opponent. Since we are using the exact same
get_player_move function, Move 3–1 will
receive a grade of 1.
• This might be a bit confusing as both our victory
and our loss will receive grades of 1. We need to
remember that this function call belongs to our
opponent, and his victory is our loss and vice
versa.
• Move 3–1 receives a grade of 1 and Move 3 will
receive a grade of -1.

13. • In this manner, these function continues to explore moves
and consequent moves. This process will continue until:
It finds a move graded with 1, in which case it will return the
move immediately.
It will continue until each possible move has a grade. The
possible moves (with grades 0 and -1) are stored in an array
• The array will then be:
a) randomized.
b) sorted from high to low.
c) the first element will be returned.

14. • These steps guarantee that:
– A losing move will be avoided unless it’s the only option
– The computer player can play diversely