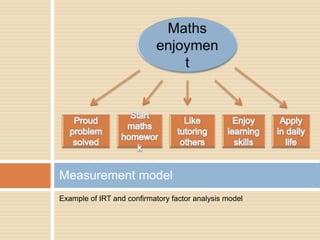
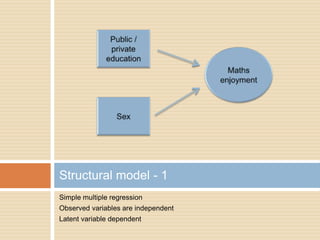
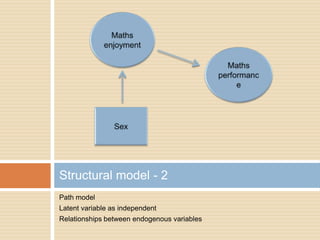
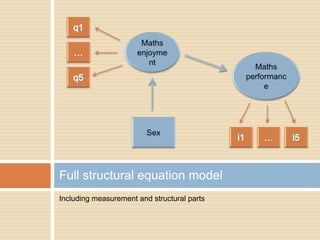
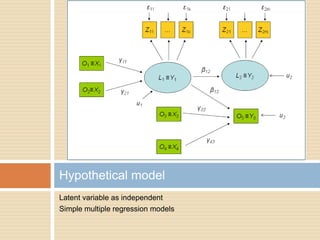
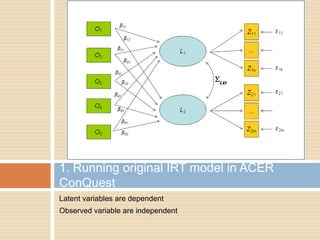
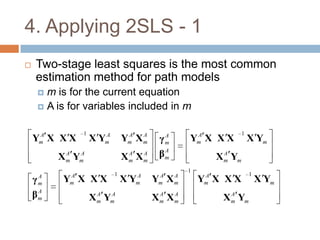
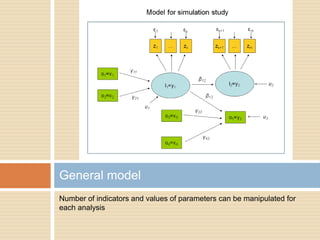
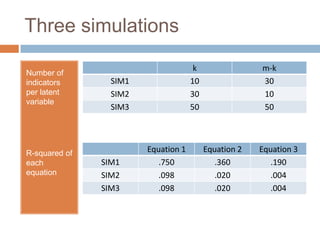
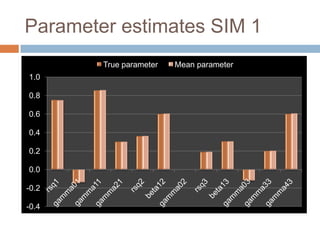
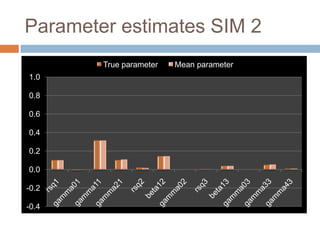
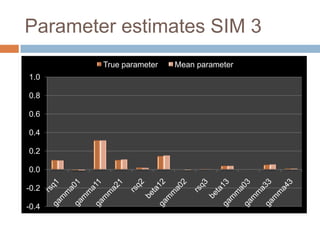
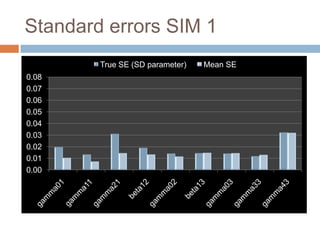
This document describes a PhD thesis that aims to bridge the gap between item response theory (IRT) and structural equation modeling (SEM). It discusses how the two approaches are formally equivalent but have some differences in their measurement and structural models. The thesis involves describing matching IRT and SEM models, estimating structural models in SEM using two-stage least squares, and adding structural features to current IRT models. A simulation study is used to evaluate the accuracy of structural parameter estimates from a multi-step approach compared to true parameters and estimates from other software programs. Results show the regression coefficients, R-squared values, and standard errors are estimated accurately.

1. BRIDGING THE GAP
BETWEEN ITEM
RESPONSE THEORY AND
STRUCTURAL EQUATION
MODELLING
PhD thesis Eveline Gebhardt

2. Background
 Two related traditions: IRT and SEM
 Measuring constructs (IRT)
 Relationships between constructs (SEM)
 Formally equivalent
 Some remaining differences:
 IRTmore flexibility measurement models
 And in data structure and guessing parameter
 SEM more flexible structural models
 SEM quicker

3. Measurement model
Example of IRT and confirmatory factor analysis model

4. Structural model - 1
Simple multiple regression
Observed variables are independent
Latent variable dependent

5. Structural model - 2
Path model
Latent variable as independent
Relationships between endogenous variables

6. Full structural equation model
Including measurement and structural parts

7. PhD thesis
 Describing similarities and differences
between the measurement models of IRT and
SEM
 Finding matching models
 Describing estimation of structural models of
SEM (2SLS)
 Adding structural features to current IRT
models
 Testing and applying of additional features

8. Expanding structural features
 Multi-step method
1. Run original IRT model in ACER ConQuest
2. Construct SSCP matrix of the structural part
from CQ output and permute this matrix
3. Apply two-stage least squares (2SLS)
estimation method

9. Hypothetical model
Latent variable as independent
Simple multiple regression models

10. 1. Running original IRT model in ACER
ConQuest
Latent variables are dependent
Observed variable are independent

11. 2. Using OLS equations - 1
 To obtain the full SSCP of the structural model
LL LO
SSCP
OL OO
 From ACER ConQuest’s output:
 conditional ˆc
covariance matrix of latent variablesO(
L|
)
ˆ
 regression c
B coefficients between latent and
observed variables ( )

12. 2. Using OLS equations - 2
 Imagine a general regression model
L = OΒ + U
 With the OLS equations
1
Β=LO OO
1
UU LL LO OO LO
 We can construct each part of the SSCP using
the ConQuest parameters from previous slide

13. 2. Using OLS equations - 3
ˆ
L O Bc O O
OL ˆ
O O Bc
L'L = U ¢ + L'O (O'O ) (L ¢ )¢
-1
U O
¢
U ˆ ˆ
= U ¢ + Bc (Bc (O ¢ ))
O
U ˆ O ˆ
= U ¢ + Bc (O ¢ )B c¢
ˆ ˆ O ˆ
= Σ cL O (N - K ) + Bc (O ¢ )B c¢
( )
é ù
UU ˆ O ˆ ˆ
éL¢ L¢ ù ê ¢ + Bc (O¢ )Bc¢ Bc (O¢ )ú
L O O
SSCP = ê ú= ê ú
ê ¢ O¢ ú ê
ë L
O Oû
ê
ë O ˆ
(O¢ )Bc¢ O¢ ú
O úû

14. 3. Permuting the original SSCP
 Latent and observed variables are redefined
as endogenous (Y) and exogenous (X)
variables
 Endogenous variables are being explained by the
model (l1, l2, o5)
 Exogenous variables only explain other variables
(o1, o2, o3, o4)
 And *then reordered using the following
Y'Y Y'X
SSCP
structure
X'Y X'X

15. 4. Applying 2SLS - 1
 Two-stage least squares is the most common
estimation method for path models
 m is for the current equation
 A is for variables included in m
A 1 A A A A 1
Ym X X X X Ym Ym X m γm
A
Ym X X X X Ym
A A
X m Ym A A
Xm Xm βm
A
A
X m Ym
1
A 1 A A A A 1
γ A
m
Y X XX
m XY m Y X
m m Ym X X X X Ym
β A
m
A A
X m Ym A A
Xm Xm A
X m Ym

16. 4. Applying 2SLS - 2
 Additional estimates
 Standard errors
1
A 1 A A A
2
Y X XX
m XY
m Y X
m m
S s
A A A A
X m Ym Xm Xm
 Explained variance
ee
R2 1 2
2 1
Ym N Ym

17. Simulation study
 Part 1 - estimated structural parameters were
evaluated by comparing them with the true
structural parameters and their standard error
 Part 2 - the same structural parameters were
compared with parameters as estimated by the
2SLS procedure in SPSS and a path model
procedure in Mplus.
 Part 3 - results from the full model, including the
measurement model, were compared between the
multi-step approach and a structural equation
model using Mplus

18. Simulation study – part 1
 Generate student responses using known
(true) parameters of a hypothetical model (100
replications)
 Running original IRT model in ACER
ConQuest
 Applying multi-step method
 Compare average estimates with true
parameters

19. General model
Number of indicators and values of parameters can be manipulated for
each analysis

20. ,
Set of three equations
 Equation 1
,
 Equation 2
 Equation 3

21. Three simulations
k m-k
Number of
indicators SIM1 10 30
per latent SIM2 30 10
variable
SIM3 50 50
R-squared of Equation 1 Equation 2 Equation 3
each SIM1 .750 .360 .190
equation SIM2 .098 .020 .004
SIM3 .098 .020 .004

22. Parameter estimates SIM 1
True parameter Mean parameter
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4

23. Parameter estimates SIM 2
True parameter Mean parameter
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4

24. Parameter estimates SIM 3
True parameter Mean parameter
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4

25. Standard errors SIM 1
True SE (SD parameter) Mean SE
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
0.00

26. Standard errors SIM 2
True SE (SD parameter) Mean SE
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
0.00

27. Standard errors SIM 3
True SE (SD parameter) Mean SE
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
0.00

28. Conclusions
 Regression coefficients are accurately
estimated
 R-squared estimates are accurately estimated
 Standard errors are equal to standard errors
from 2SLS in SPSS, but different from the SD
of the 100 estimates of each parameters
 Measurement error should be included in the
standard errors when measurement model is
included in the full model