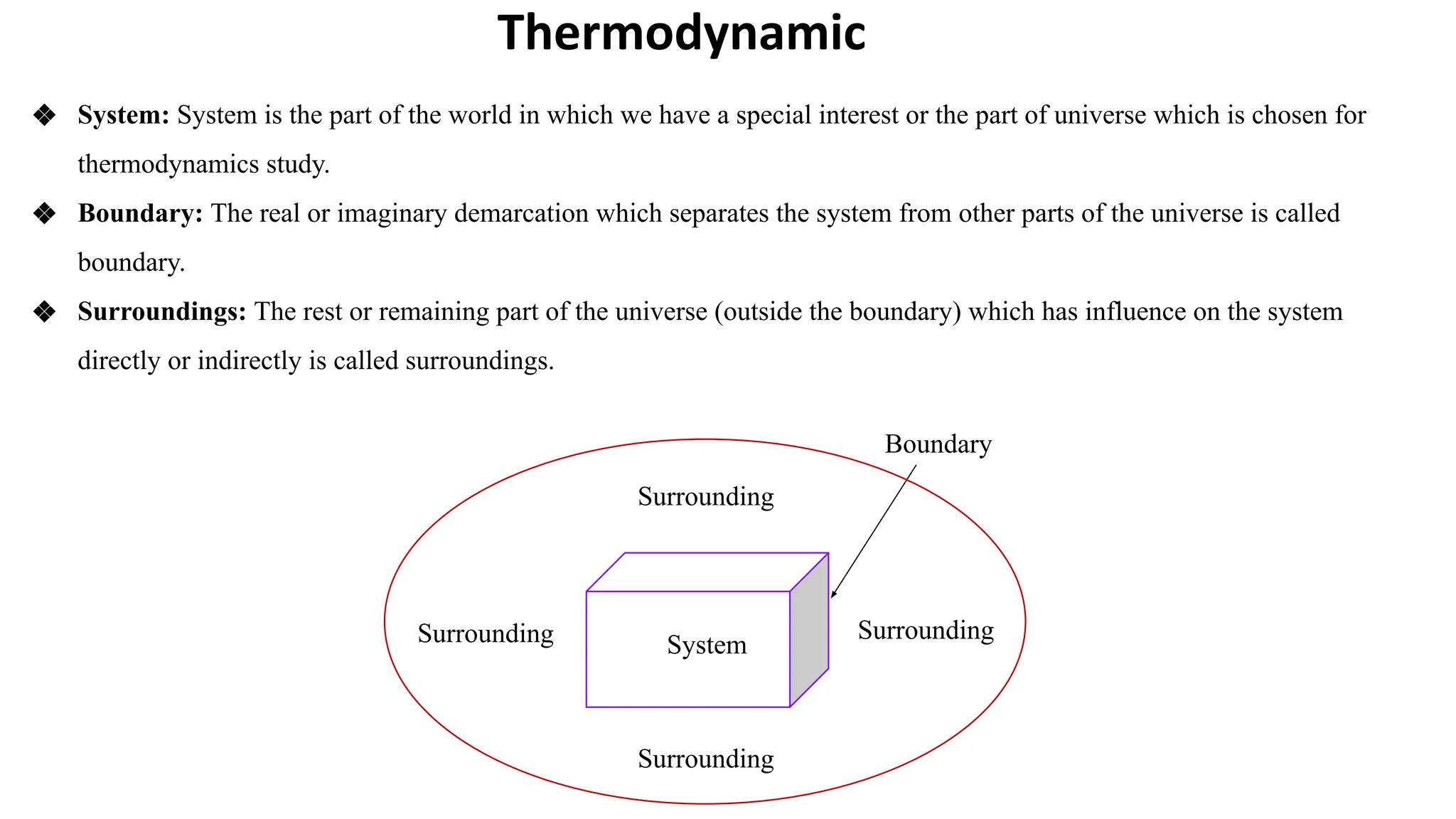
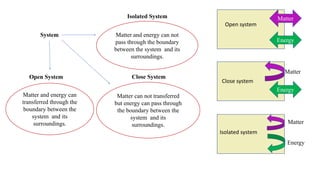
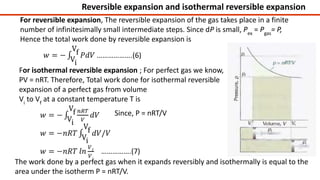
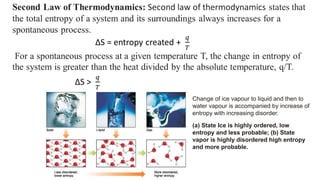
Thermodynamics is a branch of physics that deals with the relationships between heat, work, temperature, and energy. It describes how thermal energy is converted to and from other forms of energy and how matter is affected by these processes. Thermodynamics is fundamental in science and engineering, especially in fields such as mechanical engineering, physical chemistry, and energy systems.

1. ❖ System: System is the part of the world in which we have a special interest or the part of universe which is chosen for
thermodynamics study.
❖ Boundary: The real or imaginary demarcation which separates the system from other parts of the universe is called
boundary.
❖ Surroundings: The rest or remaining part of the universe (outside the boundary) which has influence on the system
directly or indirectly is called surroundings.
System
Surrounding
Surrounding
Surrounding
Surrounding
Boundary
Thermodynamic

2. Matter
Energy
Energy
Matter
Matter
Energy
System
Open System Close System
Matter and energy can
transferred through the
boundary between the
system and its
surroundings.
Matter can not transferred
but energy can pass through
the boundary between the
system and its
surroundings.
Matter and energy can not
pass through the boundary
between the system and its
surroundings.
Isolated System
Open system
Close system
Isolated system

3. Energy of a system is its ability or capacity to do work.
Heat is defined as the energy that flows into or out of a system because of a difference in temperature between the
system and its surroundings.
Enthalpy (denoted H) is an extensive property of a substance and it represents total heat content of a system.
Enthalpy of a system is express by the sum of internal energy and pressure volume work. H = U+ PV
The change in enthalpy for a reaction at a given temperature and pressure (called the enthalpy of reaction) is
obtained by subtracting the enthalpy of the reactants from the enthalpy of the products.
Thus ∆H = Hfinal
- Hinitial.
∆H = H(products) - H(reactants)
An extensive property is a property that depends on the amount of substance present in the system. Volume, Mass,
enthalpy, entropy. Gibbs Free Energy.
Let us consider a glass of water. If we double the mass of water, the volume is doubled and so is the number of
moles and the internal energy of the system.
Intensive Property is a property which does not depend on the amount of the matter present in the system, e.g.
pressure, temperature, density, and concentration. If the overall temperature of a glass of water (our system) is
20o
C, then any drop of water in that glass has a temperature of 20o
C.

4. A state function is a property of a system that depends only on its present state, which is determined by
variables such as temperature and pressure, and is independent of any previous history of the system. This
means that a change in enthalpy does not depend on how the change was made, but only on the initial state
and final state of the system.
An exothermic process is a chemical reaction or a physical change in which heat is evolved .
CH4
(g) 2O2
(g) + CO2
(g) 2H2
O(l). ∆H = - 890 kJ.
An endothermic process is a chemical reaction or a physical change in which heat is absorbed.
N2
(g) + 3H2
(g) = 2NH3(g); ∆H= 91.8 kJ
Isothermal Processes
The processes in which the temperature remains constant are called isothermal processes. For an isothermal
process dT = 0
Adiabatic Processes
The processes in which no heat can flow into or out of the system, are called adiabatic processes. For an
adiabatic process dq = 0
Isobaric Processes
The processes which take place at constant pressure are called isobaric processes. For an isobaric process dp =
0

5. Isochoric Processes
Those processes in which the volume remains constant are known as isochoric processes. For isochoric processes dV = 0.
Reversible Process
A reversible process consists of infinite number of steps for a small change of system. A reversible process must be such
that if the change of the system is done in opposite direction along the same path, then the magnitude of change of
thermodynamic quantities in different stages will be same as in the forward direction but opposite sign.
Irreversible Process:
When a process goes from the initial to the final state in a single step and cannot be carried in the reverse order, it is said to
be an irreversible process.
The heat of reaction (at a given temperature) is the amount of heat required to return a system after completion of the
reaction.
Kinetic energy is the energy associated with an object by virtue of its motion. An object of mass m and speed or velocity v
has kinetic energy Ek
equal to Ek
= 1/2 mv2
Potential Energy: is the energy associated with an object by virtue of its position. Ep
= mgh
Internal Energy: Total energy of a system is called its internal energy, U. it includes kinetic, potential energy, vibrational
energy, rotational energy and translational energy of the molecules in the system.

6. Consider a gas is confined by a frictionless piston of area, A. Suppose, an external
pressure (Pex
), equal to the pressure of the confined gas (Pgas
), is exerted on to the piston,
the magnitude of the force acting on the outer face is F =Pex
A. If the System expands
through a distance dz against the external pressure Pex
. The work done is
dw = - Pex
Adz = Pex
dV------(3)
Total work don when the volume changes from Vi
to Vf
is
If the external pressure is constant through out the expansion process, then
A
A
dz
Pex
Pgas
Expansion works at constant pressure:
Pex

7. For reversible expansion, The reversible expansion of the gas takes place in a finite
number of infinitesimally small intermediate steps. Since dP is small, Pex
= Pgas
= P,
Hence the total work done by reversible expansion is
For isothermal reversible expansion ; For perfect gas we know,
PV = nRT. Therefore, Total work done for isothermal reversible
expansion of a perfect gas from volume
Vi
to Vf
at a constant temperature T is
Since, P = nRT/V
The work done by a perfect gas when it expands reversibly and isothermally is equal to the
area under the isotherm P = nRT/V.
Reversible expansion and isothermal reversible expansion

8. First Law of Thermodynamic:
Consider a work (w) is done on a system and the energy (q) is transferred as a heat to the
system, then, the resulting internal energy change (∆U) is written as
∆U = ∆ q + ∆ w………(1)
This equation is called first Law of thermodynamic. The equation states that the change in
internal energy of a closed system is equal to the energy that passes through its boundary
as heat or work. For infinitesimal change the above equation can be written as
dU = dq + dw………(2)
First Law of Thermodynamic:

9. Or, dH = dU + PdV+VdP
Or, dH = dq+dw + PdV+VdP ( According to first
law, dU = dq+dw
Now if the system is in mechanical equilibrium
with its surroundings at constant pressure and
does only expansion work, then, dw = - PdV,
therefore,
dH = dq - PdV + PdV+VdP
or, dH = dq +VdP ( Since pressure is constant
dP = 0)
Or, dH = dq ( at constant pressure)
Consider, a infinitesimal change in the
state of a system, internal energy change
from U to U+dU, P changes to P+dP, and
V changes to V+ dV, therefore, the
enthalpy (H) change from U+PV to
H+dH = (U+dU) + (P+dP)(V+dV)
= U + dU + PV +PdV+ VdP + dPdV
= U + dU + PV +PdV+ VdP
(Since, both dP and dV is infinitesimally
small, so their product(dPdV) can be
neglected)
Hence, H+dH = H + dU +PdV+ VdP (
Since H = U + PV )
dH = qp
at constant pressure.

10. Change of ice vapour to liquid and then to
water vapour is accompanied by increase of
entropy with increasing disorder.
(a) State Ice is highly ordered, low
entropy and less probable; (b) State
vapor is highly disordered high entropy
and more probable.

11. The enthalpy change in a chemical or physical process is similar whether it is
carried out in one step or in several steps.
Hess’s Law
Let us suppose that a substance A can be changed to Z
directly.
A → Z + Q1 ∆H = – Q1
where Q1
is the heat evolved in the direct change. When
the same change is brought about in stages :
A → B + q1
∆H2 = – q1
B → C + q2
∆H2 = – q2
C → Z + q3
∆H2 = – q3
The total evolution of heat
= q1
+ q2
+ q3
= Q1

12. △G(reaction) = Σ△G(product) - Σ△G(reactants)
Hess’s Law can be used to determine other state functions with enthalpies like
free energy and entropy.
△S(reaction) = ΣS(product)- ΣS(reactants)
Formation of Enthalpy Determination:
There are various compounds including Co, C6
H6
, C2
H6
, and more, whose direct
synthesis from their constituent elements cannot be possible. Their △H values
are determined indirectly using Hess’s law.
Calculating Standard Enthalpies of Reaction
From the standard enthalpies of the reactants and products’ formation, the
standard enthalpy of the reaction is calculated by using Hess’s law.
Σ△f
Ho
(P) = Σ△f
Ho
(R) + Σ△R
Ho
=˃ Σ△R
Ho
= Σ△f
Ho
(P) - Σ△f
Ho
(R) = Sum of the standard enthalpies of
products’ formation − Sum of the standard enthalpies of reactants’ formation.

13. Determination of Heat of Transition
The heat of transition of one allotropic form to another can also be
calculated with the help of Hess’s law.
For example, the enthalpy of transition from monoclinic sulphur to rhombic
sulphur can be calculated from their heats of combustion which are :
(i) Srhombic
+ O2
(g) → SO2
(g) ∆H = – 291.4 kJ
(ii) Smonoclinic
+ O2
(g) → SO2
(g) ∆H = – 295.4 kJ
Subtracting equation (ii) from (i) we get
Srhombic
– Smonoclinic
+ O2
(g) – O2
(g)→ SO2
(g) – SO2
(g), ∆H = – 291.4 – (– 295.4)
=˃ Srhombic
= Smonoclinic
∆H = 4.0 kJ
Thus, heat of transition of rhombic sulphur to monoclinic sulphur is 4.0 kJ.

14. Heat capacity at constant pressure and Heat capacity at constant volume:

15. Relationship between Cp
and Cv
:
From definition of enthalpy,
H = U + PV
=˃ H =U+ nRT
For 1 mole of ideal gass
=˃ H = U + RT
Differentiating with respect to temperature

16. It is experimentally verified that if a reaction is carried out at different temperature the heat
changes in the reaction would be different. Kirchhoff equation expressed the dependence of
heat of reaction on temperature.
Differential form of Kirchhoff’s equation: Heat of reaction at constant pressure is
Kirchhoff equation
Differentiation of both sides of the equation with respect to absolute temperature at constant
pressure gives,
We know that,
Hence, it can be written

17. Integrated form of Kirchhoff’s equation: From the differential form of Kirchhoff’s equation we
have,
This equation is known as integrated form Kirchhoff’s equation. According to this equation heat
of reaction at higher temperature(T2
) minus heat of reaction at lower temperature(T1
) divided
by the difference of temperature is equal to change of heat capacity.