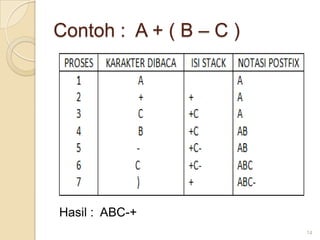
Dokumen tersebut membahas tentang struktur data dan algoritma konversi notasi infix ke postfix. Secara singkat, dibahas tentang pengenalan stack dan cara mengkonversi ekspresi matematika dari bentuk infix ke postfix menggunakan algoritma yang melibatkan penggunaan stack. Operator diproses berdasarkan level hirarkinya dan ditulis hasilnya secara berurutan tanpa operator.

1. STRUKTUR DATA
SILABUS :
• Pengenalan struktur data
• Stack
• Rekursif : - Bilangan Faktorial
- Perkalian bilangan asli
- Bilangan Fibonanci
- Permutasi
• Pemrograman pascal : - Struktur bahasa
- Tipe data
- Fungsi dan Prosedur
• Antrian
• Senarai
• Pohon
1

2. Penulisan Ungkapan Numeris
:
Salah satu pernyataan tumpukan
adalah untuk menulis ungkapan
menggunakan notasi tertentu.
Bahwa penulisan ungkapan numeris
digunakan tanda kurung untuk
mengelompokkan bagian mana yang
harus dikerjakan terlebih dahulu.
Sebagai contoh : (A+B)*(C-D)
2

3. Berbeda cara menyelesaikannya jika tidak
diberi tanda kurung. Seperti A+B*C-D.
Cara penulisan ungkapan sering disebut
dengan notasi infix yang artinya adalah
bahwa operator ditulis diantara dua
operand. Seorang ahli matematika Jan
Inkasiewicz menuliskan perkembangan
ungkapan numeris :
1. Infix yaitu operator ditulis diantara 2 buah
operand. Contoh : x + y
2. Prefix yaitu operator ditulis mendahului 2
buah operand. Contoh : +xy
3. Postfix yaitu operator ditulis setelah 2
operand. Contoh : xy +
3

4. Untuk melakukan konversi dari infix ke
postfix perlu diperhatikan level dari
operatornya yang ada pada pernyataan
infix tersebut. Operator yang memiliki
level tertinggi akan diproses terlebih
dahulu dan terhadap operator yang
selevel maka yang akan diproses lebih
dahulu adalah operator yang pertama
ditemukan.
Level operator :
1. ^ atau $ (pangkat)
2. * dan / (kali dan bagi)
4

5. Contoh – contoh :
I. Konversi infix ke prefix ?
infix  prefix
x+y+xy
 A=P+Q*R
maka :
Q*R = *QR…..1
P + 1 = +P1
= +P*QR
5

6.  B = P+Q-R
 C= (P+Q)*R
 Z = A-B*(C^D-E*G)/(M-
P^Q)^R
 A = M*N-P+Q*R/S^T/U*V
 N = (X+Y)-Z^W
 P = A+B/C-D^W
 X = A^B/C-D*E+F^G
6

7. II. Konversikan infix ke
postfix?
A = P+Q*R
Q*R = QR*…..1
P + 1 = P1+…..2
= PQR*+
 B = P+Q*(R-S)
 C= ( (P*Q)-R+S)*(V-W+Z*(M*T) )
 D= (X^Y-Z)*(M-N*(O^P)*(Q-R/S))+V
7

8. II. Konversikan infix ke
postfix?
A = P+Q*R
Q*R = QR*…..1
P + 1 = P1+…..2
= PQR*+
 B = P+Q*(R-S)
 C= ( (P*Q)-R+S)*(V-W+Z*(M*T) )
 D= (X^Y-Z)*(M-N*(O^P)*(Q-R/S))+V
8

9. Algoritma Logic ke Postfix
Menggunakan Stack
Untuk melakukan konversi dari infix ke
postfix dalam algoritmanya diperlukan
sebuah stack yang berisikan operator,
dimana setiap operator dimasukkan
kedalam stack harus diperhatikan
hirarki/level dari operatornya dengan
ketentuan :
1. Jika ada pada stack operator + atau –
kemudian diikuti oleh operator yang lebih
tinggi level hirarkinya maka operator
tersebut dimasukkan kedalam stack. Misal
= P+Q*R
9

10. 2. Jika operatornya selevel maka
operator pertama yang berada
dalam stack dieksekusi terlebiha
dahulu dan operator kedua dipush
kedalam stack. Misal :
P*Q/R
10

11. 3. Jika didalam stack level opratornya
lebih tinggi dari oprator yang akan
masuk maka langsung eksekusi
operator pertama dan push operator
kedua dalam stack.
Misal : P*Q+R
11

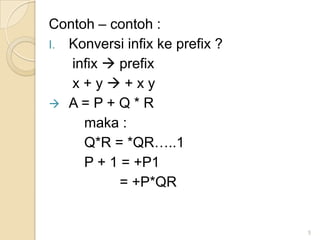
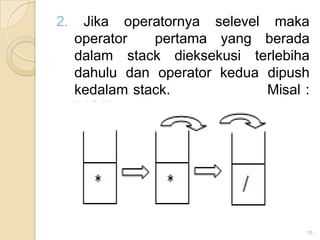
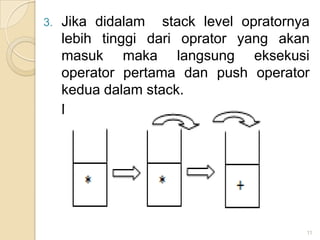
12. Algoritma Infix ke Postfix
Langkah I :
Baca ungkapan dalam notasi infix
Langkah II :
Dimulai dari I sampai N, kerjakan langkah-
langkah berikut :
a. R = S [ I ]
b. Test nilai R jika R adalah :
1. Operand : langsung ditulis
2. Kurung buka : push kedalam stack
3. Kurung tutup : pop dan tulis semua
isi tumpukan sampai ujung stack (TOS),
POP juga tanda ( tapi tidak ditulis.
12

13. 4. Operator
 Jika stack kosong atau level R lebih tinggi
dibanding level operator pada TOS, push R
(operator kedalam stack)
 Jika tidak POP ujung stack dan tulis
kemudian ulangi pembandingan R dengan
TOS kemudian R di PUSH. Kurung buka
dalam stack dianggab mempunyai level
lebih rendah diabnding R.
Langkah III :
Jika akhir notasi infix telah tercapai dan
tumpukan masih belum kosong POP
semua isi stack dan tulis hasilnya.
13

14. Contoh : A + ( B – C )
Hasil : ABC-+
14

15. Kerjakan Latihan Berikut :
S=P+Q/R–S+T
T=(X*Y)–Z^W
N=A+B/C–D^W
B=P+Q*(R–S)
15