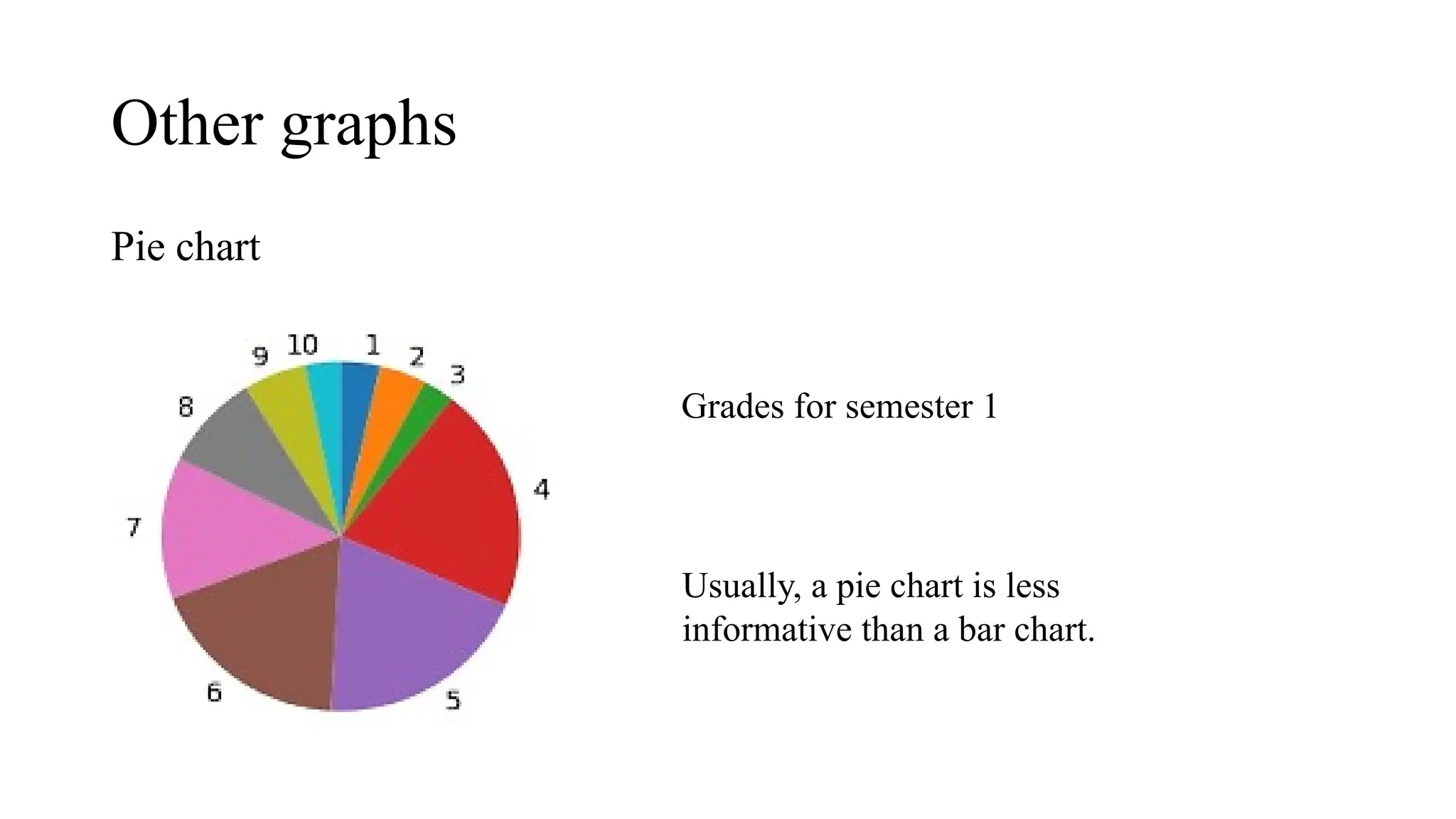
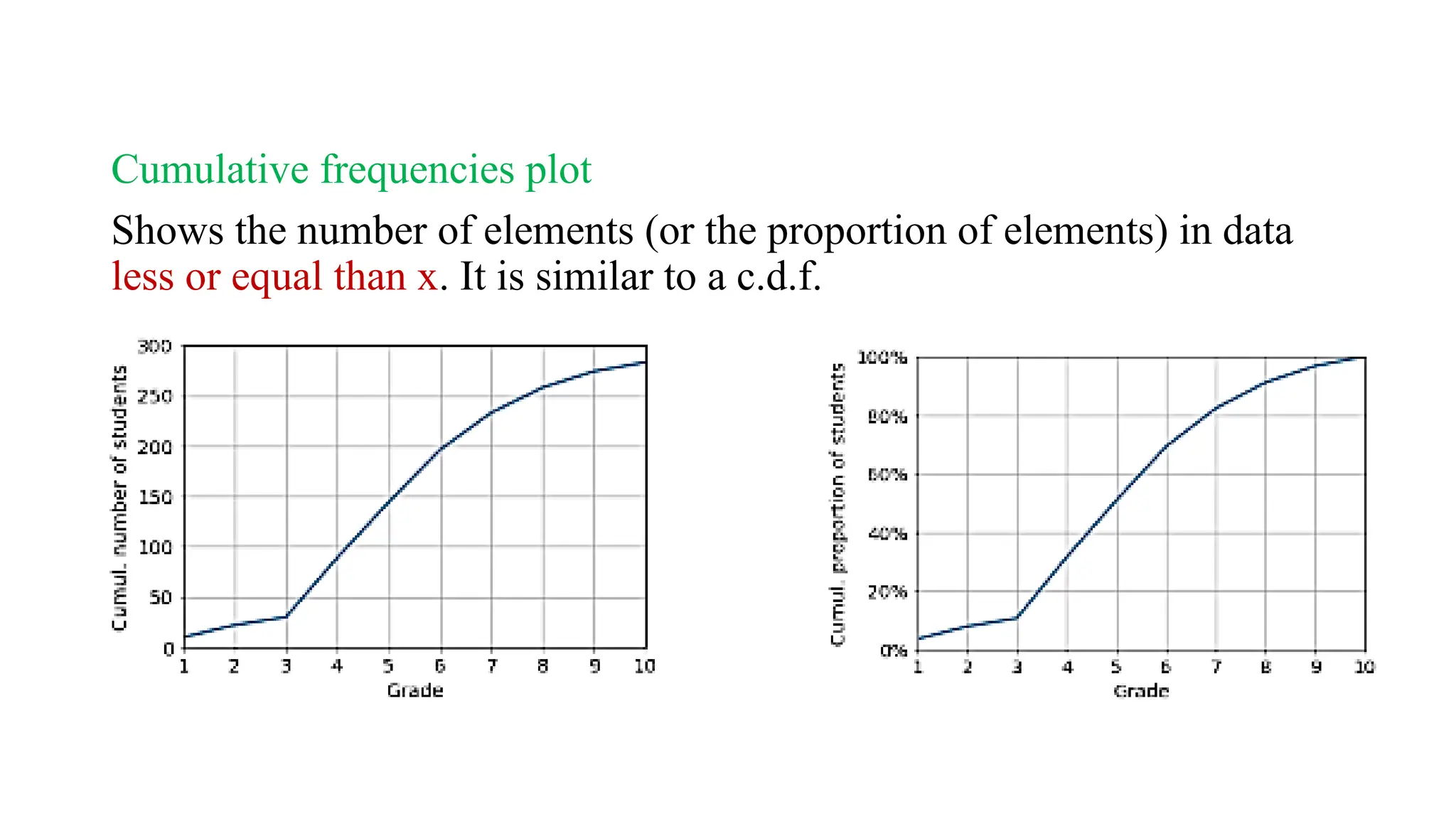
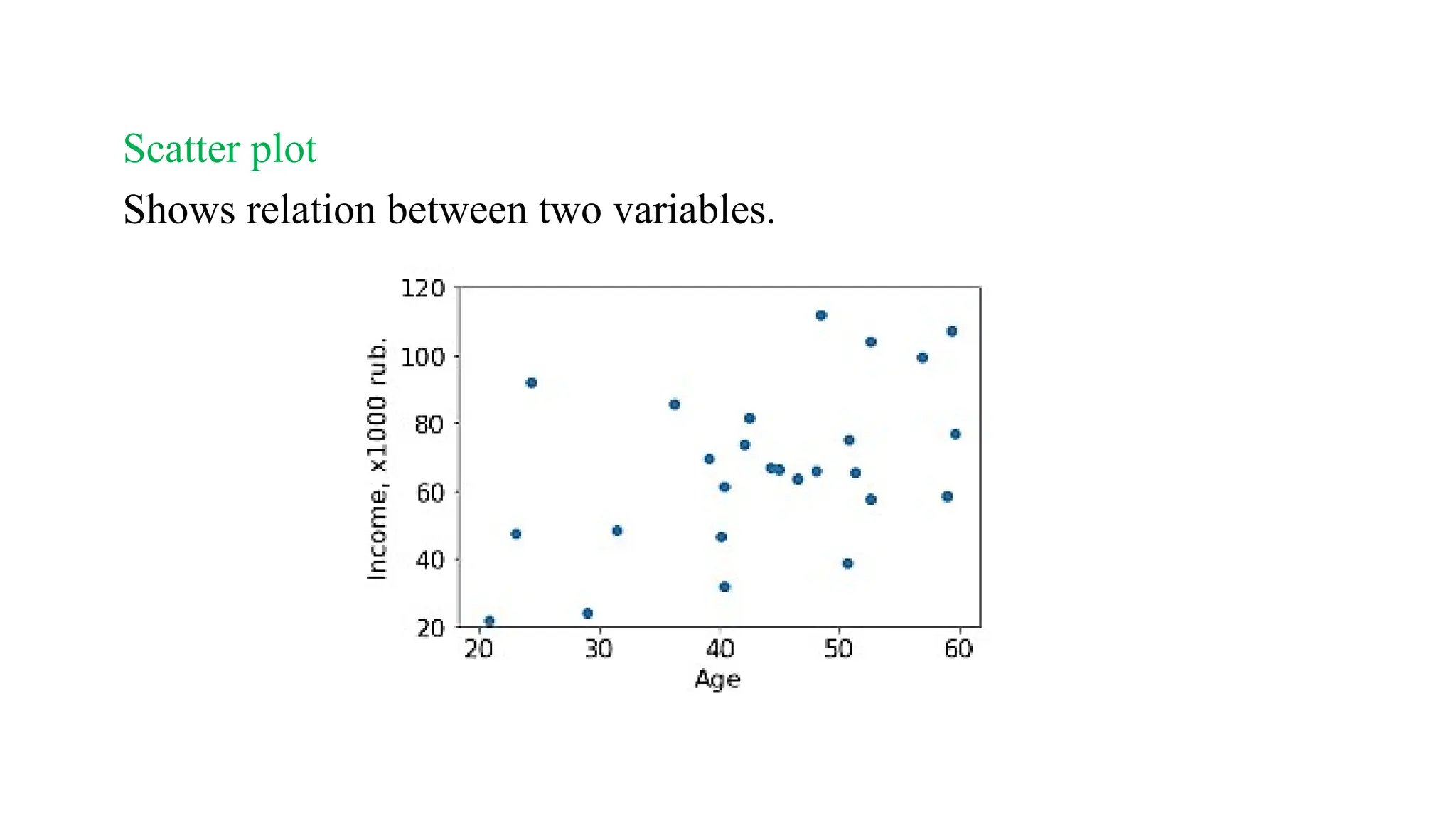
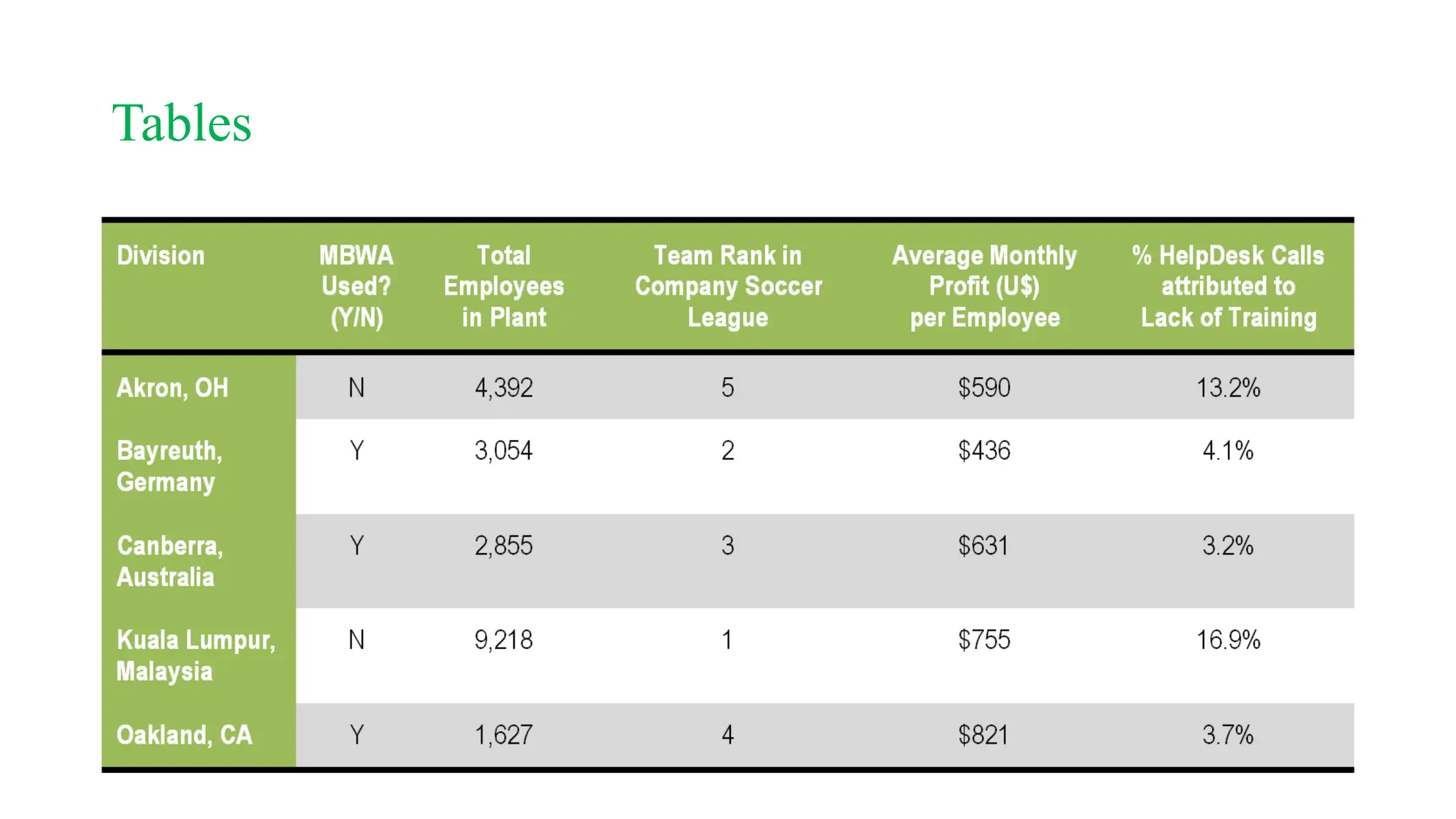
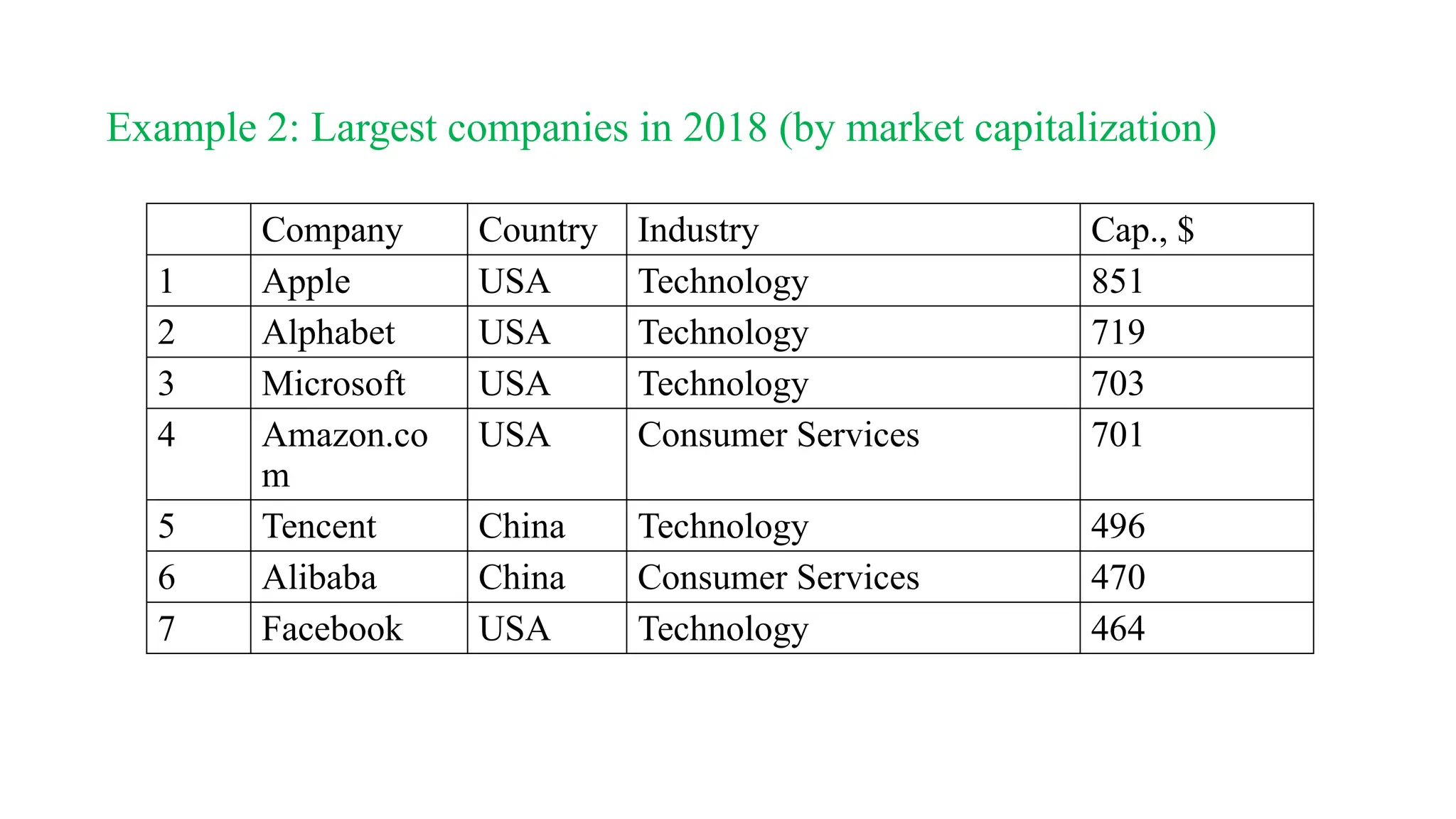
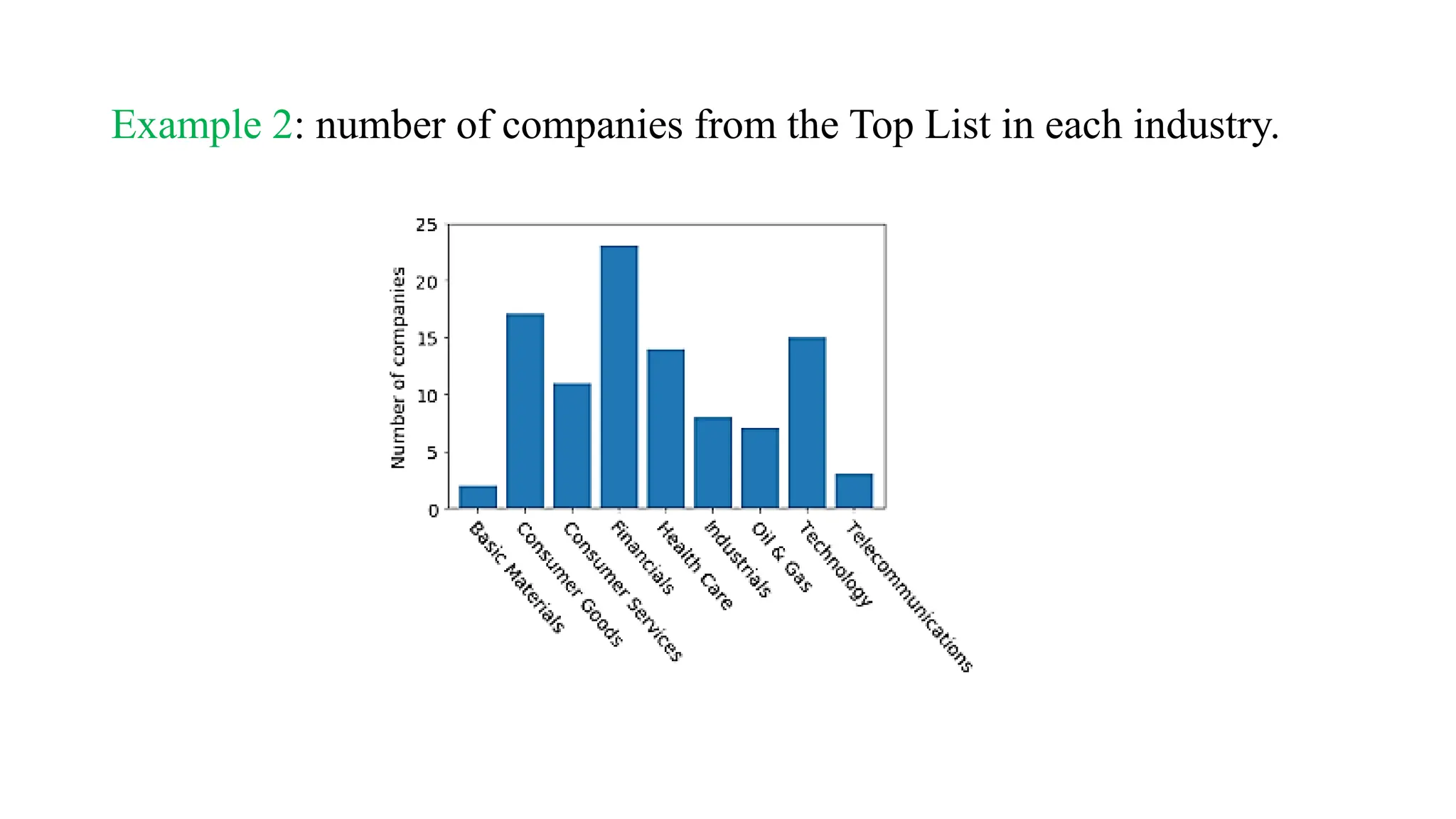
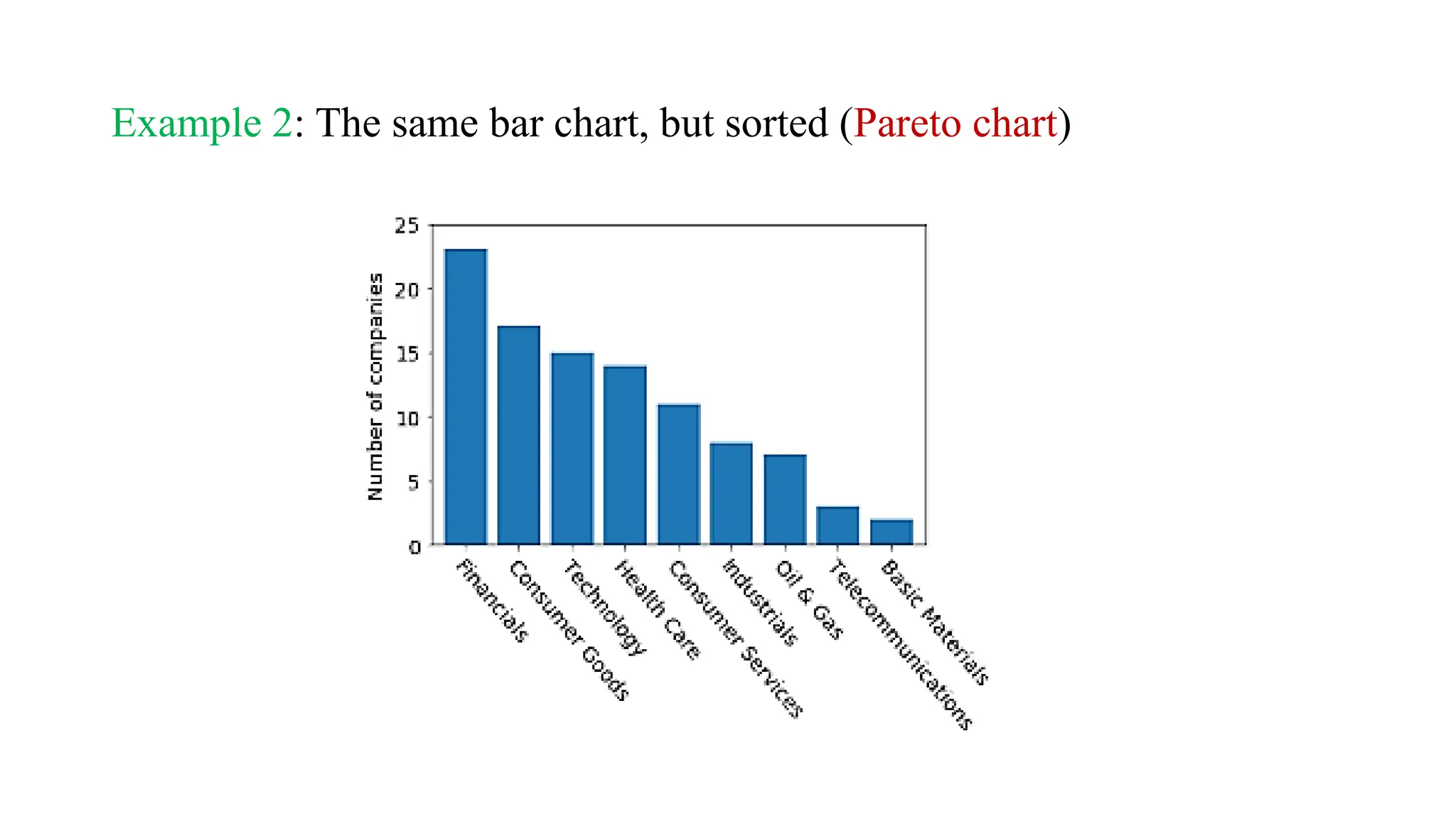
The document outlines a statistics course, detailing course rules, grading systems, and the importance of statistics in data analysis and decision-making. It distinguishes between descriptive and inferential statistics, discusses populations and samples, and provides multiple examples of applied statistics in various fields such as business, finance, and information technology. Additionally, it covers types of data, data representation methods, and various graphical techniques for visualizing data.

1. Lecture 1.
Statistical Graphs
• Statistics. Data
• Populations and Samples
• Graphical Representation of Data
Statistics

2. Course rules:
• Do not be late.
• No smart phones in class.
• All the lectures and notes will be available at iuhdportal.uni.tm.
• Every student must have 3 notebooks. ( lecture, practice, SIW)
• Be active
• Submit on time

3. Grading system
30% - midterm exam
45% - final exam
25% - SIW 40%
- lecture notes 40%
- group project 50%
- Extra points

4. Statistics
Statistics is a science about data: how to collect, analyze, present, and
interpret data.
Statistics – is a branch of applied mathematics and important in
everyday life.
- helps to make informed decisions
- understand risks
- follow the news
- conduct research
- make predictions about the future based on past data.

5. Two branches of statistics:
• Descriptive statistics organizes data by using tables, graphs, and
numerical measures.
• Inferential statistics makes decisions or predictions about a population
based on data from a sample.

6. Example:
A statistician collected data of software developers’ income per project
in Turkmenistan: 10,000; 15,000; 100,000; 130,000; 140,000, . . . . . .

7. Example:
A statistician collected data of software developers’ income per project
in Turkmenistan: 10,000; 15,000; 100,000; 130,000; 140,000, . . . . . .
Examples of questions arising in statistics:
• How to collect data? How to select people participating in the study?
• How to summarize data? For example, what is the average income,
spread of incomes, etc. of selected people?
• What can be said about the whole population? For example, how to
estimate the average income of all software developers in the country?
• How accurate are obtained estimates? How can they be improved?

8. Populations and samples
A population is a complete set of all items that interest a statistician.
Examples
• all people living in a country
• grades of all students in a university
• history of temperature observations in a city
A sample is a subset of population available for analysis
Examples
• a group of selected people
• marks of 2 students from each academic group
• temperature during the last year

9. A population is often too large for analysis and in this case the
analysis is performed on a sample. A sample can accurately
represent the whole population if the sample is chosen in a
right way

10. Applied Statistics
 Business
What’s the range of estimated sales next year that has a 95% chance of
being correct?
A manager maintaining inventory needs to know how many products
are being sold at which time of year so she can place orders before she
runs out of materials.
Supervisors have to monitor the quality of their production lines and
service levels to spot problem areas, inefficient processes, and people
who need to improve their knowledge, skills, and performance.

11. Applied Statistics
 Business
Sales managers need to know which customers:
• Buy the most?
• And which complain the most?
• Are increasing their purchase levels the fastest?
• Which salesperson has reduced productivity the most in the last
quarter?
• Is the reduction in sales by this salesperson due to chance alone or
could there be something else going on?

12. Applied Statistics
 Business
 Marketing managers ask about the millions of dollars spent on
several advertising campaigns; are any of them obviously better than
the others?
• Are the differences just temporary fluctuations or are they something
we should take seriously?

13. Applied Statistics
 Finance
• Which of several brokerages has a reliable record of higher-than-
average return on investment?
• Is the share price for this firm rising predictably enough for a day-
trader to invest in it?
• What has our return on investment been for these two brands of
computer equipment over the last four years?

14. Applied Statistics
Finance
• Should we pay the new premium being proposed by our insurance
company for liability insurance?
• What is the premium that our actuaries are calculating for a fire-
insurance policy on this type of building?
• Should we invest in bonds or in stock this year? What are the average
rates of return? How predictable are these numbers?
• Which country has the greatest chance of maximizing our profit on
investment over the next decade? Which industry? Which company?

15. Applied Statistics
Management
• One of our division manager’s claims that his below-average profit figures are just
the luck of the draw; how often would he get such a big drop in profit by chance
alone if we look at our historical records?
• Another manager claims that her above-average productivity is associated with the
weekly walkabout that is part of her management-by-walking-around philosophy;
can we test that idea to see if there is any rational basis for believing her analysis?
• The Human Resources Department wants to create a questionnaire that will help
them determine where to put their emphasis and resources in internal training next
year. How should we design the questionnaire to ensure the most neutral and least
ambiguous formulation of the questions? How can we tell if people are answering
seriously or if they are just filling in answers at random?

16. Applied Statistics
 Information Technologies
 Which of these motherboards has the lowest rate of failure according
to industry studies?
 How long should we expect these LCD monitors to last before
failure?
 How is our disk free space doing? When do we expect to have to buy
new disk drives? With what degree of confidence are you predicting
these dates?

17. Applied Statistics
 Information Technologies
 Which department is increasing their disk-space usage unusually fast? Is that
part of the normal variations or is something new going on?
 Which of our department has been increasing their use of printer paper the
most over the last quarter? Is their rate of increase just part of the normal
growth rate for the whole organization or is there anything unusual that we
should investigate?
 We have been testing three different antispam products over the last six
months; is any one of them obviously better than the others?

18. Applied Statistics
 Information Technologies
 Which of our programming teams has the lowest rate of coding errors
per thousand lines of production code? Is the difference between their
error rate and those of the other team significant enough to warrant a
lecture from them, or is it just one of those random things?
 Which programmer’s code has caused the highest number of helpdesk
calls in the past year? Is that bad luck or bad programming?

19. Applied Statistics
 Life in general
 This politician claims that our taxes have been rising over the last
couple of years; is that true?
 Is using this brand of tooth paste associated with decreased chances
of getting tooth decay compared with that brand?
 Does listening to two different sounds at the same time really relate to
changes in brainwaves that make us feel calmer and be smarter?

20. What is data?
In this course, Data will be represented by a collection of values
describing particular characteristics of some objects. Values xi are called
observations.
Types of data
Quantitative data (numerical) –
are numbers Income, profit,
weight, length, temperature,
time, . . . . .
Qualitative data (categorical)
– are not numbers Yes/No,
color, brand, country,
name, . . . . .
Warning: data can be represented by numbers which have no “numerical” meaning
(example: academic group number). We treat such data as categorical.

21. Examples of qualitative data:
• Color (e.g., red, orange, yellow, etc.)
• Tone (e.g., middle-C, b-flat below middle-C)
• Timbre (e.g., oboe-sound, flute-sound, drum-sound)
• Shape (e.g., round, square, tetrahedral, etc.)
• Preference for a particular movie (e.g., like, neutral, dislike, etc.)
• Type (e.g., wool, cotton, plastic; or complaint vs praise, addiction
vs habit; etc.)
• Origin (e.g., endogenous vs exogenous; local vs foreign)

22. Examples of quantitative data:
 Primary wavelength of light reflected by an object ?
 Primary frequency of light reflected by an object ?
 Waveform of a trumpet sound expressed as Fourier transforms of a sonogram
 Length of sides of a triangle
 Number of people expressing a particular preference for a movie
 Numerical representation (e.g., a Likert scale) of a feeling (e.g., 0 = no pain, 1 =
barely noticeable pain, 2 = slightly annoying pain, … 10 = “Angel of Death
please take me now.”)

23. Example:
Occupation, gender are categorical data. Age, income are numerical data.
Examples of statistical problems:
1. Which profession is the most popular? Which is the most well-paid?
2. Is there a relation between age and income? Gender and income?
3. How much will a 25 years old male economist will earn?
Occupation Gender Age Income
Programmer Male 25 100,000
Economist Female 25 60,000
Lawyer Male 45 100,000
Dentist Female 40 80,000
Programmer Female 35 90,000

24. Tables
It is a simple table (a matrix with labels for the rows down the side and
those for the columns across the top) showing some (invented)
qualitative and quantitative data.
The focus of the study is on different characteristics of the five divisions
in the company.(Figure:1). Division can be called the identifier and the
information about the different divisions can be called observations.

25. Tables

26. The different observations about each of the specific cases of the
identifier are called variables; in this case, we have a total of six
variables because the identifier is itself a variable. All the variables are
listed in columns in this table. Two of the variables are qualitative
(sometimes described as categorical because values are categories) and
four of the variables are quantitative. Quantitative variables may be
measured, counted, or ranked.

27. Qualitative variables in our study:
• The use of MBWA (management by walking around) – qualitative.
• The name or location of the division – qualitative.
Quantitative variables:
• Total employees in plant – quantitative (counted).
• Team rank in the company soccer competitions – quantitative (rank
order).
• Average monthly profit per employee in US dollars – quantitative
(measured).
• The percentage of Help Desk calls traced to a lack of training –
quantitative (measured).

28. Graphical representation of data
Example 1: grades for the 1st semester of XYZ university students in 2020
9, 5, 6, 6, 8, 3, 7, 5, 4, 4, 6, 7, 3, 9, 7, 4, 2, 5, 4, 8, 6, 5, 4, 5, 6, 1, 7, 5, 5, 4,
7, 7, 6, 6, 6, 6, 5, 7, 8, 4, 4, 6, 4, 5, 8, 3, 4, 6, 10, 10, 4, 7, 7, 2, 6, 8, 4, 5, 7,
5, 7, 7, 5, 4, 5, 6, 4, 7, 5, 5, 5, 1, 5, 6, 5, 4, 5, 5, 6, 7, 6, 4, 4, 9, 6, 6, 4, 4, 9,
1, 6, 8, 6, 7, 8, 10, 8, 2, 2, 6, 5, 6, 8, 4, 5, 4, 9, 4, 4, 5, 7, 4, 5, 7, 10, 6, 8, 2,
6, 5, 5, 2, 7, 9, 8, 4, 7, 8, 4, 7, 6, 5, 6, 6, 6, 10, 8, 2, 5, 6, 6, 6, 5, 2, 5, 9, 8, 5,
4, 2, 8, 10, 1, 5, 4, 4, 5, 6, 10, 1, 5, 4, 5, 5, 6, 6, 4, 3, 6, 8, 7, 4, 4, 4, 7, 7, 7,
4, 8, 7, 5, 8, 4, 1, 5, 5, 5, 1, 5, 7, 10, 3, 9, 4, 8, 5, 7, 4, 6, 4, 6, 7, 3, 4, 4, 7, 4,
5, 6, 7, 9, 4, 6, 2, 5, 4, 8, 2, 4, 5, 9, 7, 8, 9, 4, 3, 4, 4, 4, 4, 6, 6, 4, 5, 9, 6, 7,
6, 7, 7, 4, 5, 8, 6, 9, 4, 1, 6, 8, 7, 7, 9, 6, 6, 5, 6, 5, 5, 9, 7, 5, 4, 6, 1, 6, 5, 4,
5, 3, 4, 8, 6, 4, 5, 10, 5, 4, 9, 2, 4, 1, 6, 8 Looking at this list, it is difficult to
make conclusions.

29. Example 2: Largest companies in 2018 (by market capitalization)
Company Country Industry Cap., $
1 Apple USA Technology 851
2 Alphabet USA Technology 719
3 Microsoft USA Technology 703
4 Amazon.co
m
USA Consumer Services 701
5 Tencent China Technology 496
6 Alibaba China Consumer Services 470
7 Facebook USA Technology 464

30. Bar Chats
A bar chart (or a bar graph) shows how many elements belong to each
of the categories. It is used for categorical data or numerical data with a
small number of different values.
Example 1: Number of students who got each grade

31. Example 2: number of companies from the Top List in each industry.

32. Example 2: The same bar chart, but sorted (Pareto chart)

33. Things to remember:
1. The heights of the bars should be proportional to the number of
elements in the categories
2. Don’t forget to label the axis
3. If necessary, sort the categories

34. Bar charts with relative frequencies
Instead of numbers of elements in each category, sometimes it is more
informative to provide proportions of values in each category.
“Numbers of elements” are also called absolute frequencies.
“Proportions of elements” are also called relative frequencies.
Example 1 (with relative frequencies)

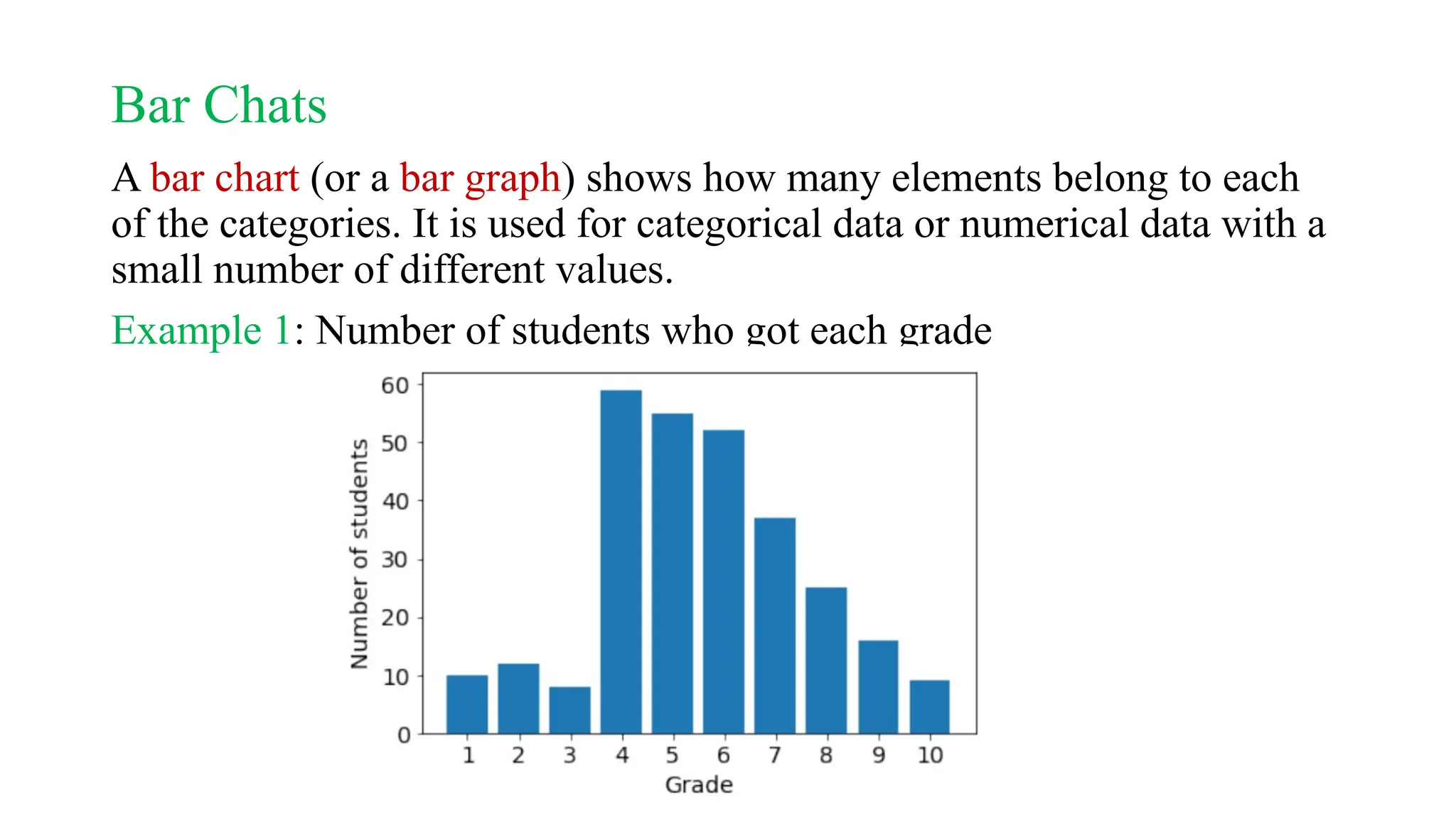
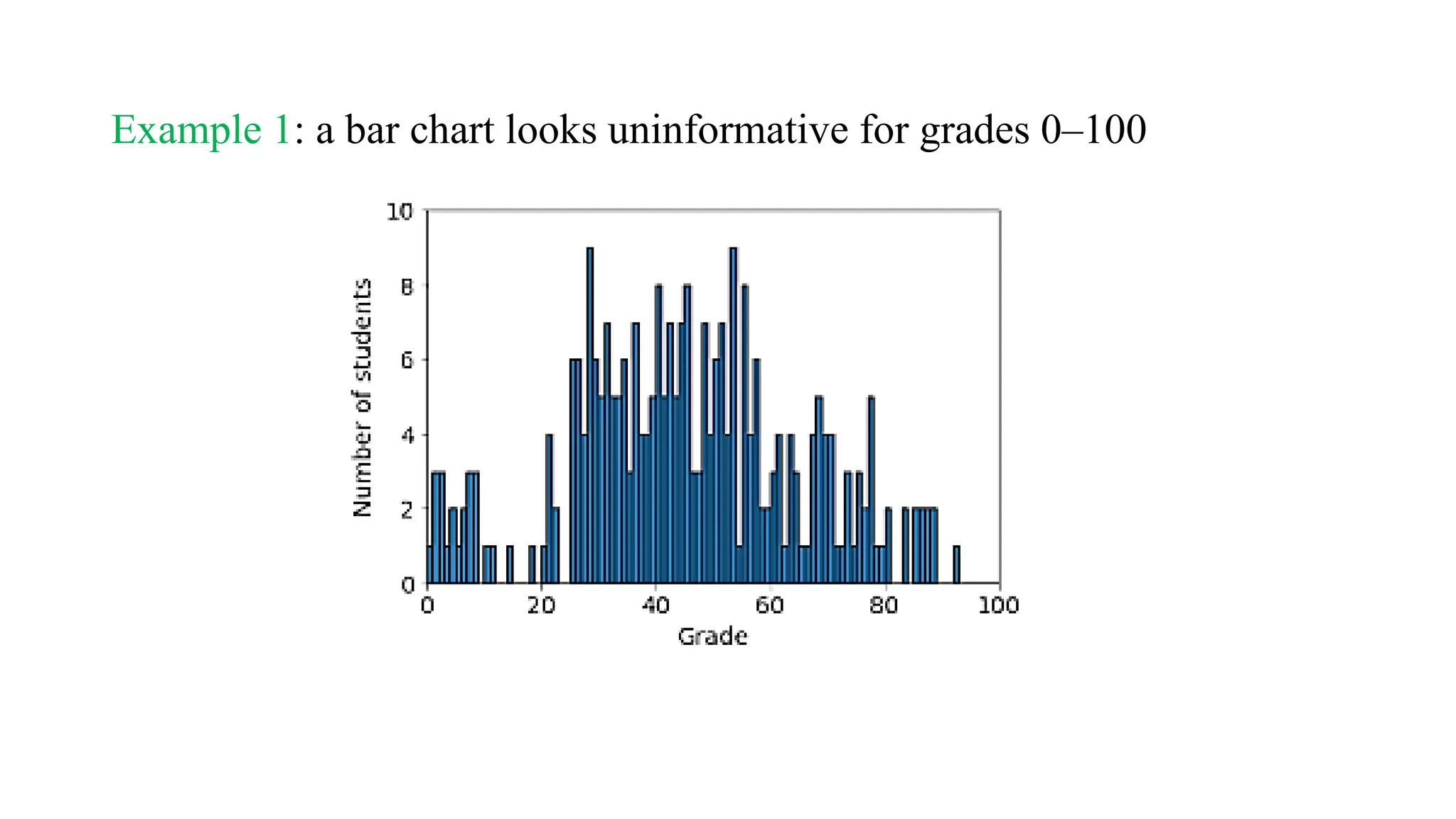
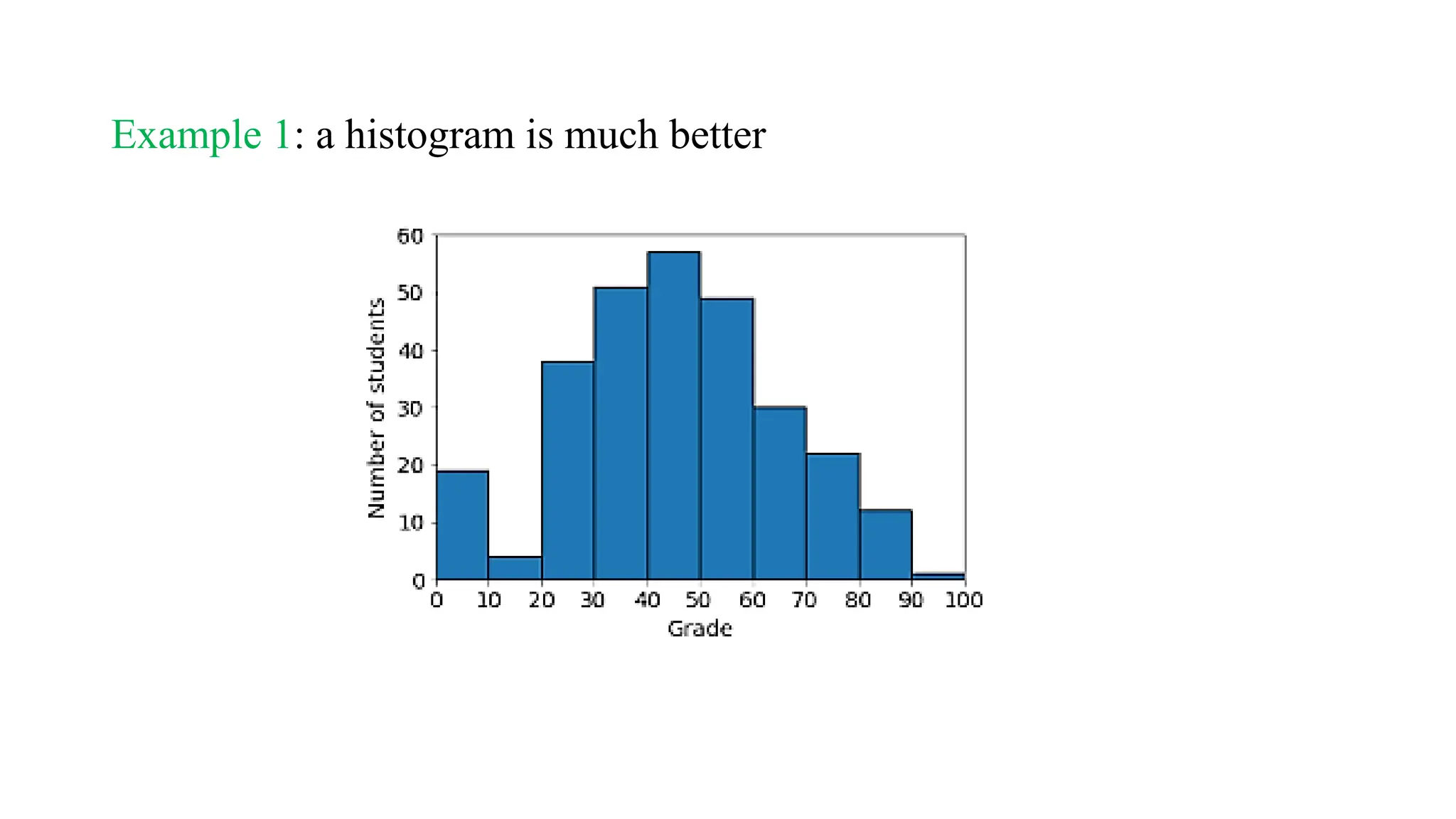
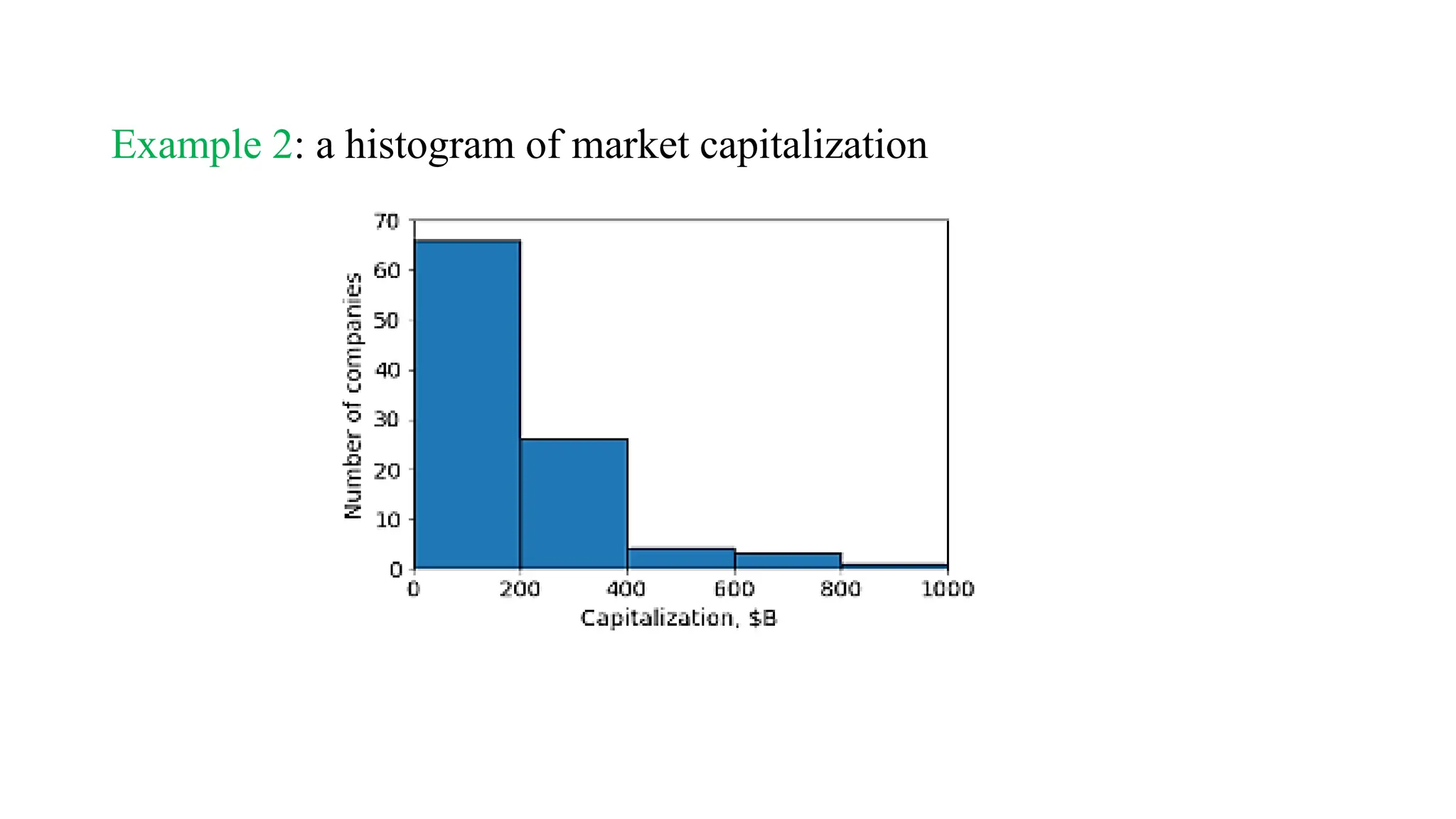
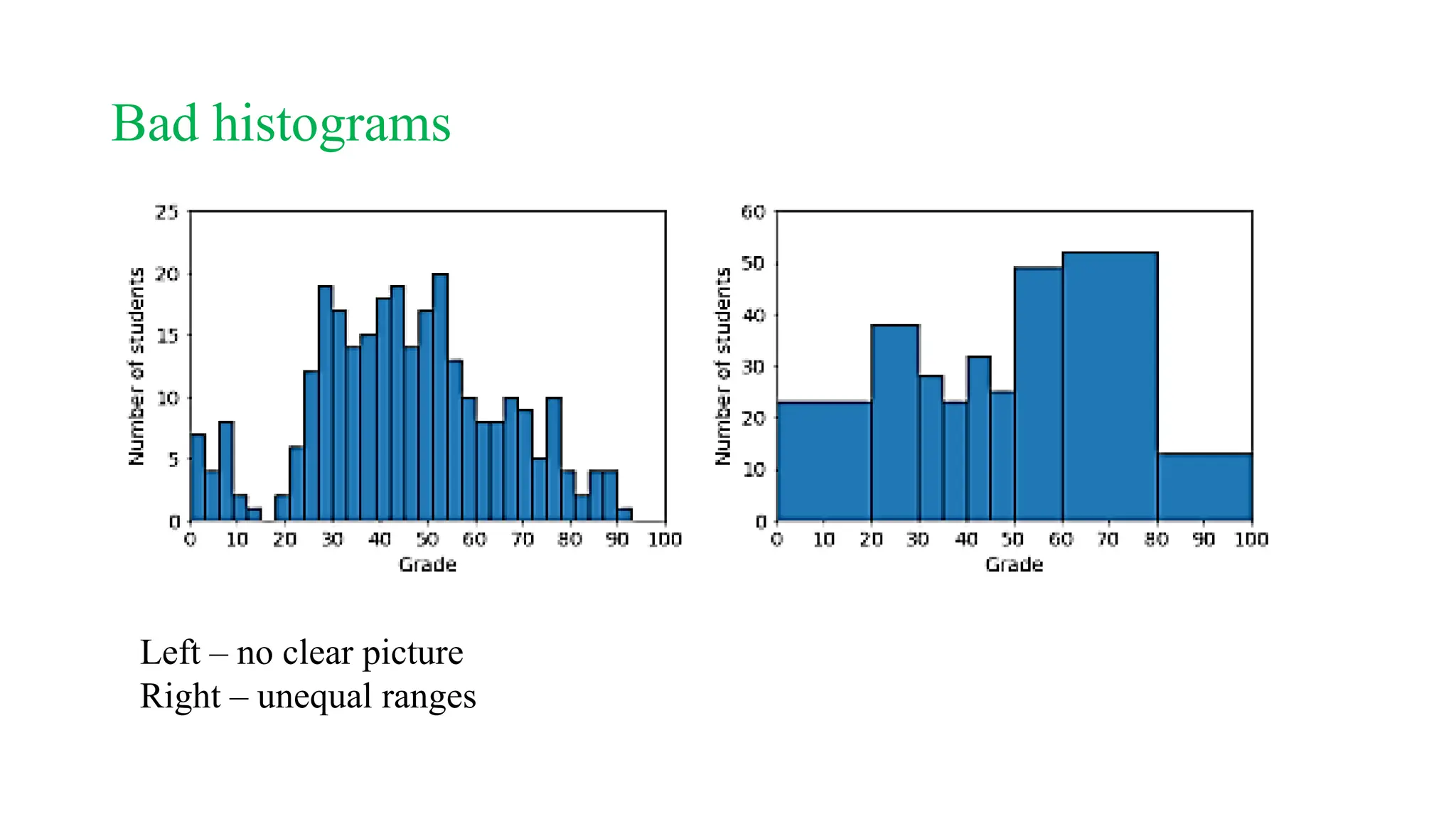
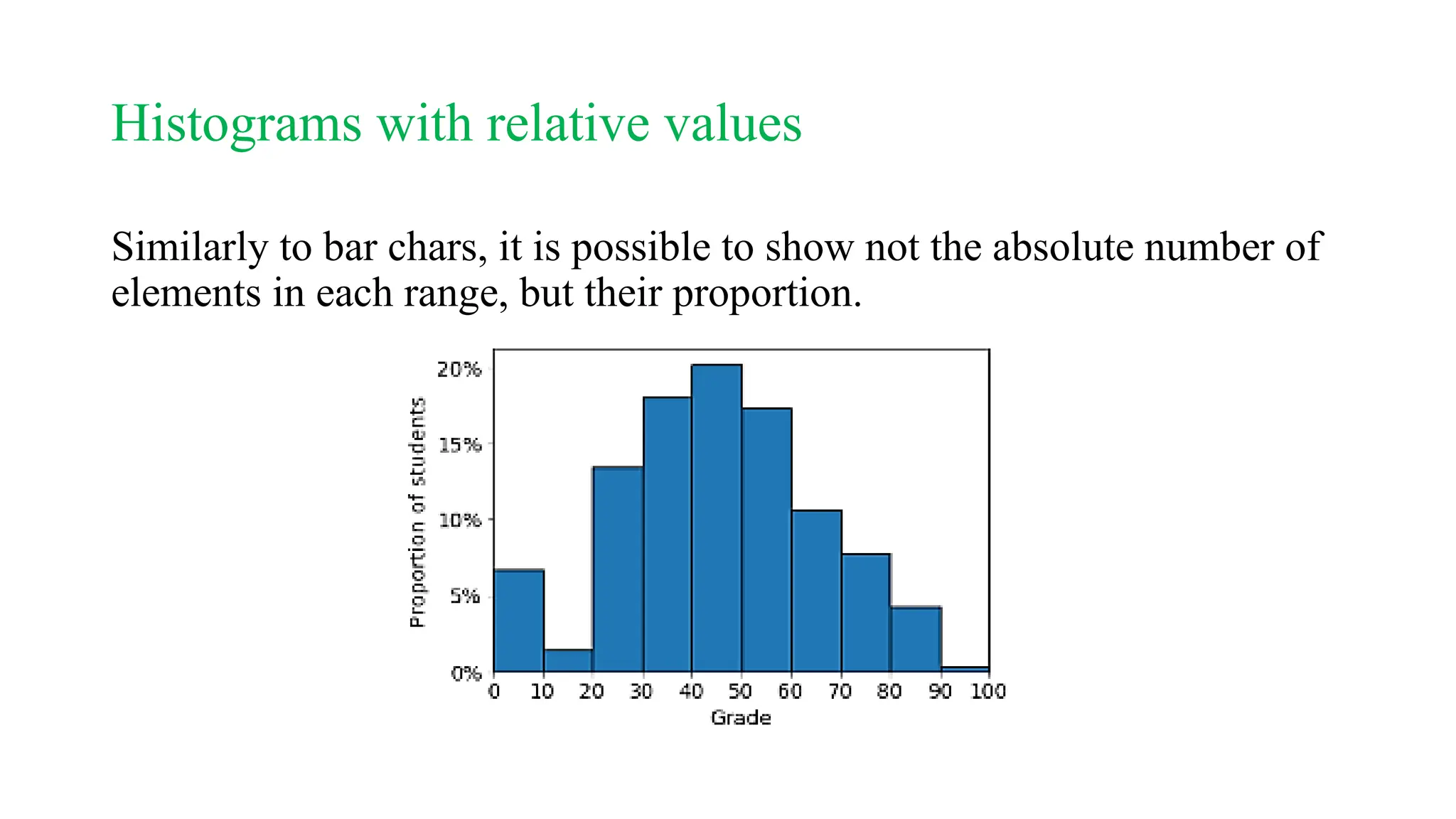
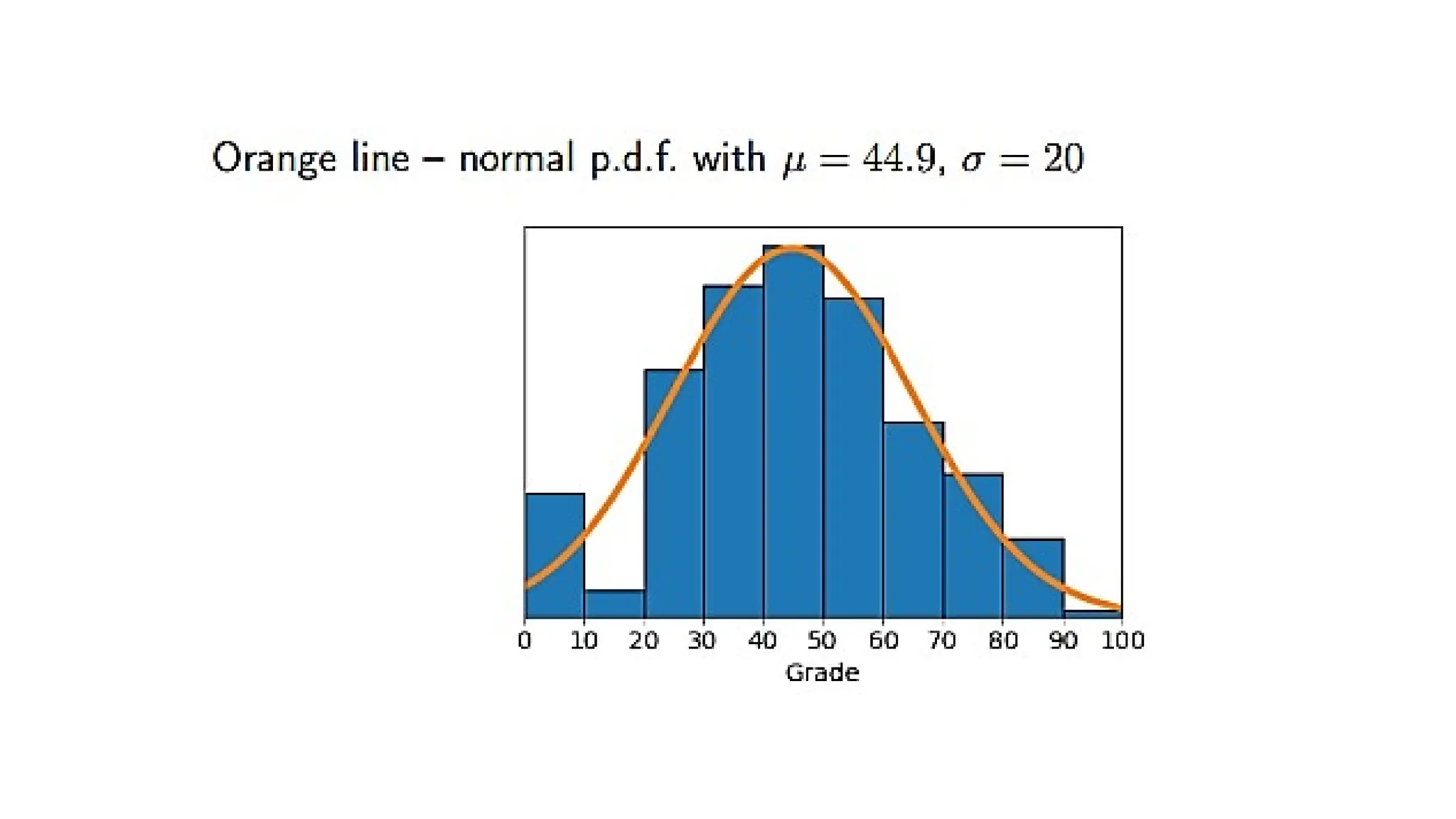
35. Histograms
A histogram is like a bar chart, but for numerical data with many
possible values.
Instead of counting the number of values in each category, we count the
number of values in ranges of values ]

36. Example 1: a bar chart looks uninformative for grades 0–100

37. Example 1: a histogram is much better

38. Example 2: a histogram of market capitalization

39. Things to remember
1. Data ranges must be of equal length; no gaps between bars
2. Choose data ranges that allow to see the general shape of data
3. Decide upon whether you use ranges closed on the right
or close on left
(Usually we prefer closed on the right – like a c.d.f. )

40. Bad histograms
Left – no clear picture
Right – unequal ranges

41. Histograms with relative values
Similarly to bar chars, it is possible to show not the absolute number of
elements in each range, but their proportion.

42. Normalized histograms and p.d.f.
If a population distribution is continuous, the shape of a histogram
resembles the graph of a p.d.f.
We can scale a histogram, so that the area under the histogram is 1 and
compare with the graph of the p.d.f. with estimated parameters (for
example, the normal p.d.f.).

44. Other graphs
Pie chart
Grades for semester 1
Usually, a pie chart is less
informative than a bar chart.

45. Stem and leaf plots
A frequency distribution can be made more visually appealing by
turning it into a stem and leaf plot. Table 3.8 shows the percentage of
males and females who were literate in 37 African countries in 1994.

46. Stem Leaf

47. Cumulative frequencies plot
Shows the number of elements (or the proportion of elements) in data
less or equal than x. It is similar to a c.d.f.

48. Scatter plot
Shows relation between two variables.