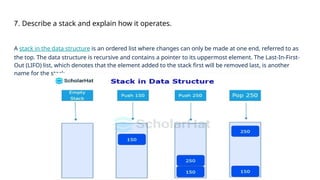
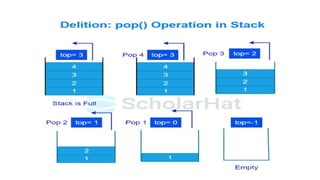
The document discusses stack data structures, highlighting their recursive nature and various operations such as push, pop, and peek. It explores the role of stacks in function call management, dynamic resizing, real-life applications, and algorithms for sorting and evaluating expressions. Additionally, it addresses stack overflow, balancing parentheses, and depth-first search implementation using stacks.

1. STACK INTERVIEW
QUESTIONS

2. 1. Why Stack is considered a Recursive data structure?
A stack is considered a recursive data structure because its definition is self-
referential. At any given point, a stack can be defined as a top element combined
with another stack (the remainder).
Whenever an element is pushed onto or popped off a stack, what remains is still a
stack. This self-referential nature, where operations reduce the problem to smaller
instances of the same type, embodies the essence of recursion

3. 2. Explain how Stacks are used in Function Call management in programming languages.
When functions are called in programming languages, the system typically uses a call stack to manage the call sequence
and memory allocation. Let's take a look at how this process works.
The Call Stack
The call stack maintains a record of all the active function calls that a program makes. When a new function is called, it's
added to the top of the stack. Once a function finishes its execution, it's removed from the stack, and control returns to the
calling function.
This "last in, first out" behavior is well-suited to stack data structures.
How the Call Stack Works
1. Function Call: When a function is called, a stack frame is created and pushed onto the call stack. This frame
contains important information about the state of the function, such as local variables and the return address, which
points to the instruction after the function call.
2. Local Execution: The CPU executes the instructions within the called function. The function accesses its inputs,
processes data, and calls other functions as needed.
3. Return: If the called function doesn't make any further function calls, it exits, and its stack frame is removed.
Alternatively, if the function makes additional calls, the call stack grows further.
4. Stack Unwinding: Once the initial (or other topmost) function call is finished, there are no more functions to execute.
The stack then shrinks, starting with the top frame, until it's empty.

4. def multiply(a, b):
result = a * b
return result
def calculate(a, b, c):
temp = multiply(b, c)
return a + temp
result = calculate(2, 3, 4)
print(result) # Output: 14

5. 3. Write algorithm to Implement a Dynamic Stack that automatically resizes itself.
Resizing a stack involves two main operations: shrinking and expanding the stack when needed. A
common strategy is to double the stack's size each time it reaches full capacity and halve it when it
becomes 25% full, as this provides efficient amortized performance.
Key Operations
1. push(item): Add an item to the stack.
2. pop(): Remove and return the top item from the stack.
3. is_full(): Check if the stack is full.
4. is_empty(): Check if the stack is empty.
5. expand(): Double the stack's capacity.
6. shrink(): Halve the stack's capacity.
Algorithm Steps
7. Start with an initial capacity for the stack. In this example, it's 2.
8. Whenever a push operation encounters a full stack, call the expand method before the addition.
9. Whenever a pop operation leaves the stack 25% full, call the shrink method.
This ensures the stack dynamically adjusts its size based on the current number of elements.

6. Complexity Analysis
● Time Complexity:
○ push: O(1) amortized. Although expand can take up to O(n) time, it is only triggered once
every n push operations, resulting in an average of O(1) per push.
○ pop, is_full, and is_empty: O(1).
○ expand and shrink: O(n) in the worst case, but they are infrequently called, so their
amortized time is O(1) per operation.
● Space Complexity: O(n) where n is the number of elements in the stack. This accounts for the stack
itself and any additional overhead such as the temporary arrays used during resizing.

7. 4. What are some real-life applications of a stack?
Stacks are widely used in real-life applications due to their LIFO behavior. Some examples include:
● Function Call Stack in Programming: When a function is called, it’s pushed onto the stack with its
local variables. Once the function finishes execution, it is popped off the stack, and the program
returns to the point where the function was called.
● Undo/Redo in Applications: In text editors, stacks can keep track of previous actions (undo).
When you press the undo button, the most recent action is popped from the stack and reversed.
● Expression Evaluation: Stacks are used to evaluate expressions in postfix (Reverse Polish)
notation and to convert infix expressions to postfix.
● Memory Management: In operating systems, the stack stores local variables and manages the
function call process.

8. 5. implement a Queue Using Stacks
class Queue:
def __init__(self):
self.enqueue_stack = []
self.dequeue_stack = []
def enqueue(self, x):
# append the new element to the enqueue stack
self.enqueue_stack.append(x)
def dequeue(self):
# if dequeue stack is empty pop all the elements
# from enqueue stack and push them onto the dequeue stack
if not self.dequeue_stack:
while self.enqueue_stack:
self.dequeue_stack.append(self.enqueue_stack.pop())
# pop the element from the dequeue stack and return it
return self.dequeue_stack.pop()

9. 6. Which type of data structure typically is used when recursion is
carried out?
The stack data structure is used in recursion in data structure
because it is last in first out. To save the iteration variables at each
function call, the operating system keeps the stack maintained.

10. 7. Describe a stack and explain how it operates.
A stack in the data structure is an ordered list where changes can only be made at one end, referred to as
the top. The data structure is recursive and contains a pointer to its uppermost element. The Last-In-First-
Out (LIFO) list, which denotes that the element added to the stack first will be removed last, is another
name for the stack.

11. 8. What kinds of operations are possible on a Stack?
There are three basic operations that can executed by stack in data structure:
● PUSH: A new element is inserted into the stack via the push action. The top of the stack is occupied by
the new feature.
● POP: The top member of the stack is removed using the pop operation.
● PEEK: A peek action does not remove the top element from the stack; instead, it returns its value.

13. 9. When evaluating arithmetic expressions utilizing the prefix and postfix forms, which notations are
used?
When evaluating arithmetic expressions using prefix and postfix forms, the following
notations are often used:
● Prefix Notation (or Polish Notation): Polish notation, often known as prefix
notation, arranges the operators before the operands.
● Postfix Notation (or Reverse Polish Notation, RPN): Reverse Polish Notation, or
RPN, often known as postfix notation, arranges the operator after the operands.

14. 10. Sort a stack using a temporary stack
Algorithm:
1. Create a temporary stack say tmpStack.
2. While input stack is NOT empty do this:
● Pop an element from input stack call it temp
● while temporary stack is NOT empty and top of temporary stack is
greater than temp,
pop from temporary stack and push it to the input stack
● push temp in temporary stack
3. The sorted numbers are in tmpStack

15. // C++ program to sort a stack using an
// auxiliary stack.
#include <bits/stdc++.h>
using namespace std;
// This function return the sorted stack
stack<int> sortStack(stack<int> &input)
{
stack<int> tmpStack;
while (!input.empty())
{
// pop out the first element
int tmp = input.top();
input.pop();
// while temporary stack is not empty and
top
// of stack is lesser than temp
while (!tmpStack.empty() &&
tmpStack.top() < tmp)
{
// pop from temporary
stack and push
// it to the input stack
input.push(tmpStack.top());
tmpStack.pop();
tmpStack.push(tmp);
}
return tmpStack;
}
// main function
int main()
{
stack<int> input;
input.push(34);
input.push(3);
input.push(31);
input.push(98);
input.push(92);
input.push(23);
// This is the temporary stack
stack<int> tmpStack =
sortStack(input);
cout << "Sorted numbers are:n";
while (!tmpStack.empty())
{
cout <<
tmpStack.top()<< " ";
tmpStack.pop();
}

16. 11.Which data structure is needed to convert infix notation to
postfix notation?
The Stack data structure is used to convert infix expression to postfix
expression. The purpose of stack is to reverse the order of the operators
in the expression. It also serves as a storage structure, as no operator
can be printed until both of its operands have appeared.

17. 12. How is a stack implemented in memory?
A stack can be implemented using arrays or linked lists. An array-based stack
uses an array to store elements and a pointer (or index) to the top element. A
linked-list-based stack uses nodes, where each node points to the next one.

18. 13. What is the "call stack" in programming?
The call stack is a special stack used by the operating system to store
information about the active subroutines or function calls in a program. It
tracks the return addresses, local variables, and the state of each
function during execution.

19. 14. How can a stack be used to check for balanced parentheses in an expression?
A stack can be used to check for balanced parentheses by pushing opening
brackets (, {, [ onto the stack. For every closing bracket ), }, or ], check if the top of
the stack contains the corresponding opening bracket. If not, the parentheses are
unbalanced.

20. 15. What is the maximum size of a stack?
The maximum size of a stack depends on the system's memory
limitations or the specific data structure used to implement the stack. For
an array-based stack, it’s limited by the size of the array. In a dynamic
array or linked list-based stack, the stack can grow as long as there is
available memory.

21. 16. What happens when a function call exceeds the stack limit?
When the stack limit is exceeded, a stack overflow occurs, typically resulting in a
program crash.

22. 17. How do you perform depth-first search (DFS) using a stack?
The DFS algorithm is a recursive algorithm that uses the idea of backtracking. It involves exhaustive
searches of all the nodes by going ahead, if possible, else by backtracking.
Here, the word backtrack means that when you are moving forward and there are no more nodes
along the current path, you move backwards on the same path to find nodes to traverse. All the nodes
will be visited on the current path till all the unvisited nodes have been traversed after which the next
path will be selected.
This recursive nature of DFS can be implemented using stacks. The basic idea is as follows:
Pick a starting node and push all its adjacent nodes into a stack.
Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack.
Repeat this process until the stack is empty. However, ensure that the nodes that are visited are
marked. This will prevent you from visiting the same node more than once. If you do not mark the
nodes that are visited and you visit the same node more than once, you may end up in an infinite loop.

23. Pseudocode:
DFS-iterative (G, s): //Where G is graph and s is source vertex
let S be stack
S.push( s ) //Inserting s in stack
mark s as visited.
while ( S is not empty):
//Pop a vertex from stack to visit next
v = S.top( )
S.pop( )
//Push all the neighbours of v in stack that are not visited
for all neighbours w of v in Graph G:
if w is not visited :
S.push( w )
mark w as visited
DFS-recursive(G, s):
mark s as visited
for all neighbours w of s in Graph G:
if w is not visited:
DFS-recursive(G, w)

24. 18. What is the difference between a stack and a heap?
Stack: Memory is managed in a Last In, First Out (LIFO) manner, used for function
calls and local variables.
Heap: Memory is managed dynamically, and memory allocation is done manually
(using malloc or free in C, for example).

25. 19. How do you handle overflow in a dynamic stack implementation?
Overflow in a dynamic stack can be handled by reallocating memory
when the stack reaches its capacity.

26. 20. What is a bounded stack?
A bounded stack is a stack with a fixed size. When the stack is full, any further
push operations will result in a stack overflow.
In a bounded stack, when the stack is full, further push operations should either
return an error or handle the overflow (e.g., by resizing the stack).

27. 21. What is stack overflow and stack underflow?
stack Overflow: Occurs when you try to add an element to a full stack. In a stack with a fixed
size, if the push operation is called when the stack is already at its maximum capacity, it results in
a stack overflow.
Stack Underflow: Occurs when you try to remove an element from an empty stack. If you call
pop() on an empty stack, it results in a stack underflow.
For example:
● In an array-based stack with a fixed size of 3, if you try to push a fourth element, it will result
in a stack overflow.
● If you call pop() on an empty stack, you’ll encounter stack underflow.

28. 22. How does a stack help with balancing parentheses?
A stack can be used to check if parentheses in an expression are balanced. The idea is to push
every opening parenthesis onto the stack. For every closing parenthesis, you pop an opening
parenthesis from the stack. If at the end of the expression, the stack is empty, the parentheses are
balanced.
Algorithm:
1. Traverse the expression from left to right.
2. For every (, {, or [, push it onto the stack.
3. For every ), }, or ], check if the stack is empty. If it is not, pop the stack. If the top of the stack
does not match the corresponding opening bracket, the expression is unbalanced.
4. If the stack is empty after processing the entire expression, the parentheses are balanced.

29. 23. How can a stack be used to solve the problem of finding the largest rectangle in a histogram?
To find the largest rectangle in a histogram, a stack can be used to efficiently calculate the area of
rectangles formed by the histogram bars. The idea is to use the stack to keep track of the indices of the
bars. As you traverse the histogram, you use the stack to calculate the maximum possible rectangle area
for each bar.
Steps:
1. Traverse the histogram from left to right.
2. For each bar:
○ If it is taller than the bar at the top of the stack, push its index onto the stack.
○ If it is shorter, pop the stack and calculate the area of the rectangle formed by the popped bar
as the shortest bar in the rectangle.
3. Continue this process until all bars are processed, then perform a final calculation for any remaining
indices in the stack.
The algorithm runs in O(n) time, where n is the number of bars in the histogram.