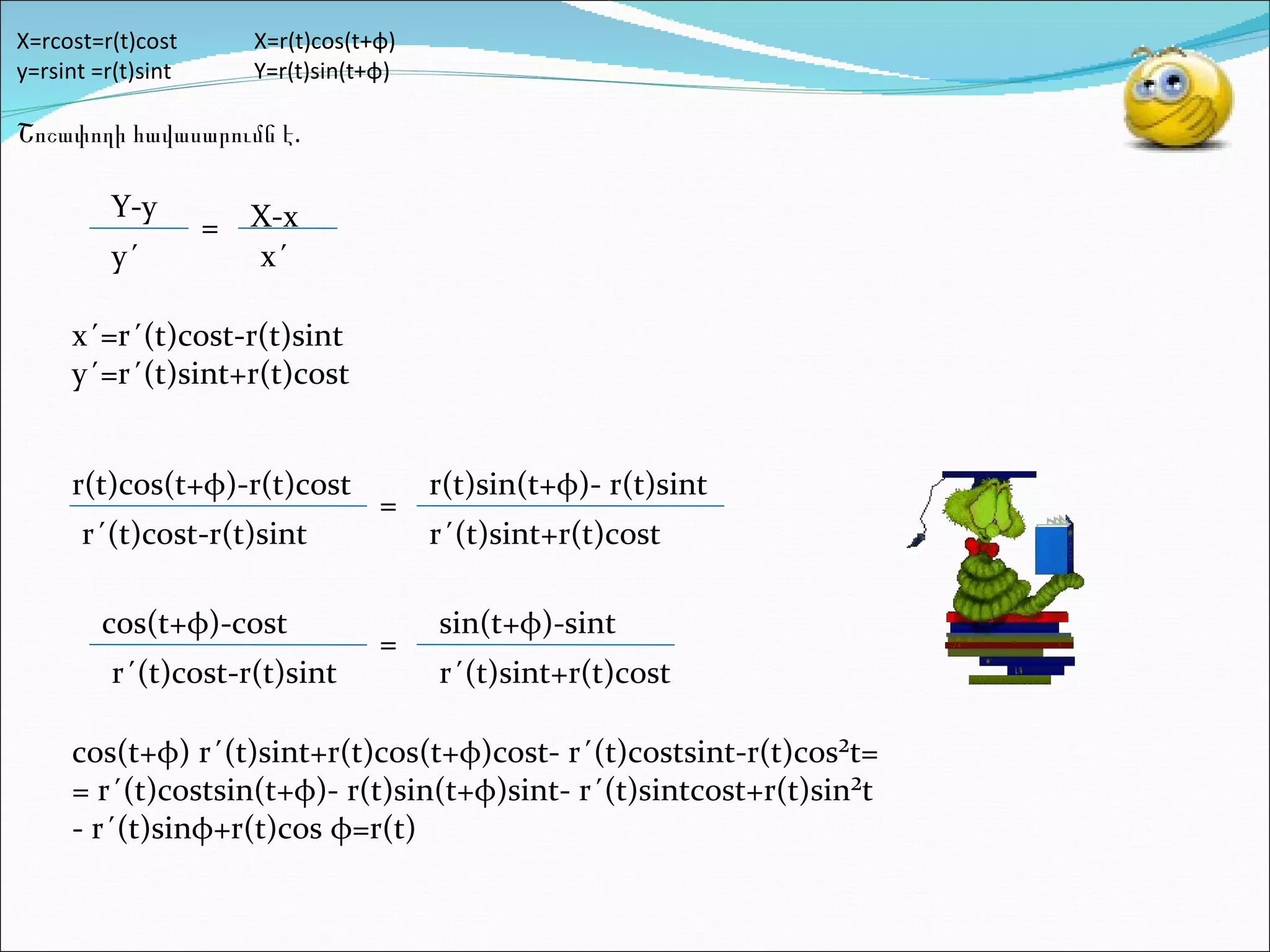
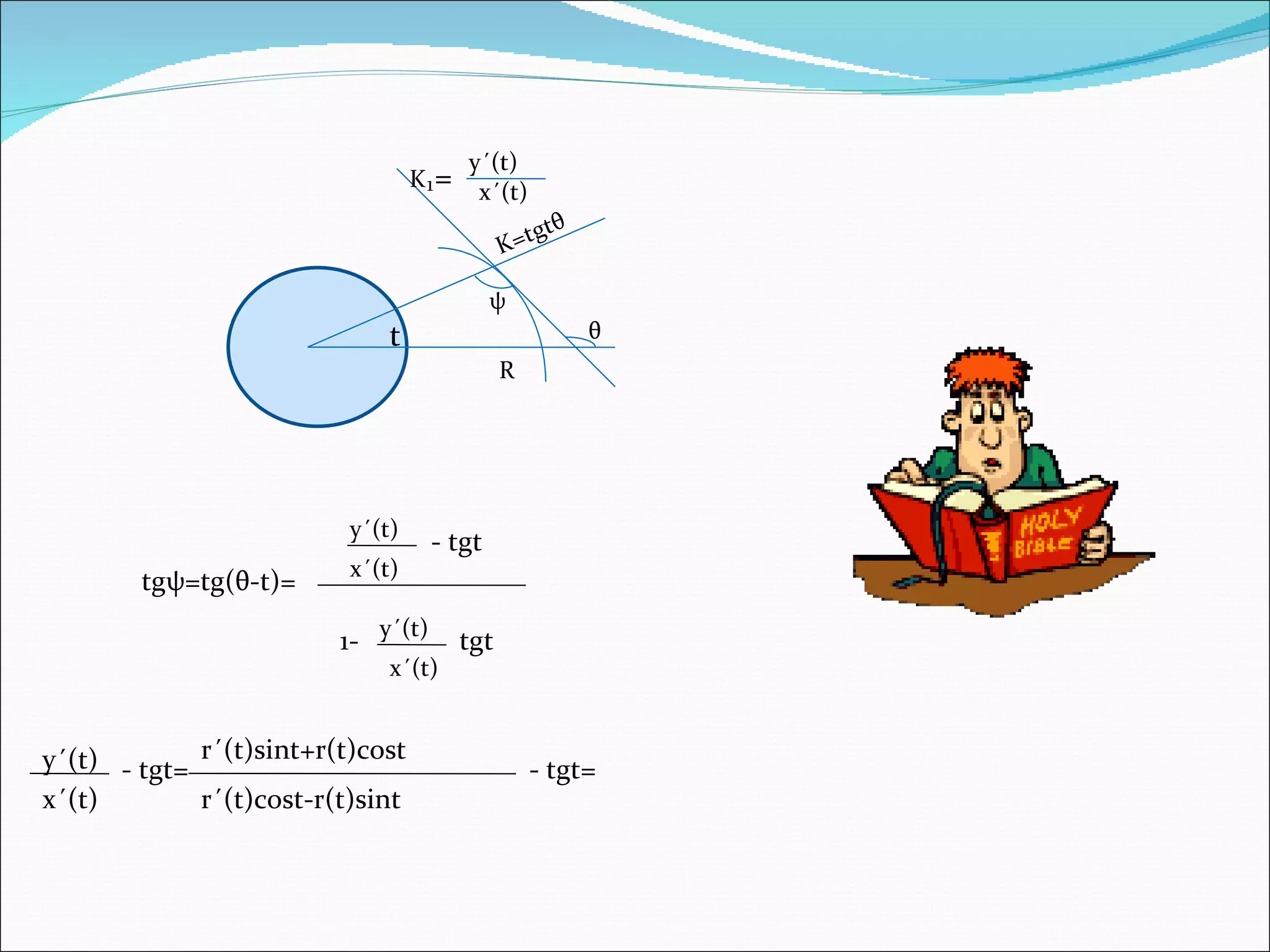
1. n կրիաներ գտնվում են շրջանագիծը հավասար մասերի բաժանող կետերում և սկսում են շարժվել դեպի կենտրոն`հետևելով մեկը մյուսին: Ի̉նչ հետագծով են շարժվում կրիաները: Ընդունել,որ կրիաների արագությունները նույնն են, և բոլորը շարժվում են ժամսլաքի հակառակ ուղղությամբ: Խնդրի դրվածքը

2. 1. Գտնել շոշափողը և պահանջել, որ անցնի B կետով: 2. Լուծել դիֆերենցիալ հավասարումը 3. Հաշվել հետագծի երկարությունը A -ից մինչև O : A x B y (x,y) t+ φ t r(t)

3. X=rcost=r(t)cost X=r(t)cos(t+ φ ) y=rsint =r(t)sint Y=r(t)sin(t+ φ ) Շոշափողի հավասարումն է. Y-y y´ = X-x x´ x´=r´(t)cost-r(t)sint y´=r´(t)sint+r(t)cost r(t)cos(t+ φ )-r(t)cost r´(t)cost-r(t)sint = r(t)sin(t+ φ )- r(t)sint r´(t)sint+r(t)cost cos(t+ φ )-cost r´(t)cost-r(t)sint = sin(t+ φ )-sint r´(t)sint+r(t)cost cos(t+ φ ) r´(t)sint+r(t)cos(t+ φ )cost- r´(t)costsint-r(t)cos²t= = r´(t)costsin(t+ φ )- r(t)sin(t+ φ )sint- r´(t)sintcost+r(t)sin²t - r´(t)sin φ +r(t)cos φ =r(t)

4. - r´(t)sin φ =r(t)(1-cos φ ) r´(t)sin φ =2r(t)sin² φ /2 -2 r´(t) sin φ /2cos φ /2=2r(t)sin² φ /2 - r´(t) cos φ /2=r(t)sin φ /2 dr dt = -rtg φ /2 dr r = -tg φ /2 dt lnr=-t tg φ /2+c lnR=c lnr=-t tg φ /2+lnR ln r R =-t tg φ /2 r R = -t tg φ /2 e r=R e -t tg φ /2

5. K₁ = y´(t) x´(t) θ ψ R tg ψ =tg( θ -t)= y´(t) x´(t) - tgt 1- y´(t) x´(t) tgt x´(t) y´(t) - tgt= r´(t)sint+r(t)cost r´(t)cost-r(t)sint - tgt= t K=tgt θ

6. = r´(t)sintcost+r(t)cos²t-r´(t)sintcost+r(t)sin²t cost(r´(t)cost-r(t)sint) = r(t) cost(r´(t)cost-r(t)sint) 1- y´(t) x´(t) tgt=1- r´(t) sin²t+r(t)costsint r´(t) cos²t-r(t)costsint = r´(t) cos²t+r´(t) sin²t cost(r´(t)cost-r(t)sint) = = r´(t) cost(r´(t)cost-r(t)sint) tg ψ = r r´ =-ctg φ /2

7. Հետագծի երկարության հաշվումը. l=∫√x´²+y´² dt=∫√ (r´(t)cost-r(t)sint)²+( r´(t)sint+r(t)cost)² dt=∫√r´²(t)+r²(t) dt= = ∫√(-Rtg φ /2 e -t tg φ /2 )²+(Re -t tg φ /2 )² dt=R√tg² φ /2 +1 ∫√e -2t tg φ /2 dt= =R√ tg² φ /2 +1 lim∫e -t tg φ /2 dt= -R√ tg² φ /2 +1 tg φ /2 lime -t tg φ /2 = R√ tg² φ /2 +1 = tg φ /2 ∞ 0 ∞ 0 ∞ 0 ∞ 0 ∞ 0 A->∞ 0 A A 0