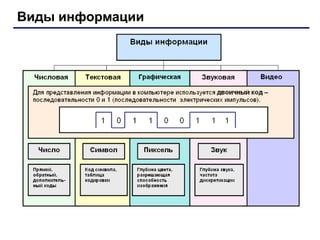
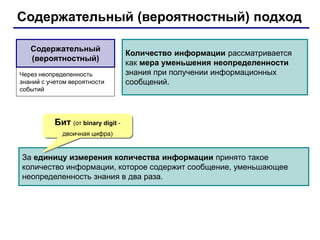
Документ описывает основы двоичного кодирования информации и единицы измерения количества информации, такие как бит и байт, а также производные единицы, включая килобайт и мегабайт. Излагается подходы к измерению информации, основанные на уменьшении неопределенности и количестве символов, с примерами задач по вычислению информации. Рассматриваются различные виды информации, такие как текстовая, графическая и звуковая, и приведены формулы для вычисления объема информации в этих типах.

1. Двоичное
кодирование
информации
Информатика 1 курс

2. Виды информации

3. Единицы измерения
количества информации

4. Производные единицы измерения
количества информации
Бит (Binary DigiT - двойная цифра)
В теории информации – наименьшая единица количества
информации.
В вычислительной технике – двоичная цифра (может
принимать значения 0 и 1), двоичный разряд.
За единицу измерения количества информации принято такое
количество информации, которое содержит сообщение, уменьшающее
неопределенность знания в два раза. Такая единица названа бит.
Байт (Byte)
В теории информации – восемь подряд идущих бит.
В вычислительной технике – наименьшая адресуемая
единица данных или памяти, равная восьми битам.

5. Байт, килобайт, мегабайт, …
Название Байт Кбайт Мбайт Гбайт
Килобайт,
Кбайт
210 = 1024
Мегабайт,
Мбайт
220 = 1048576 210 = 1024
Гигабайт,
Гбайт
230 220 = 1048576 210 = 1024
Терабайт,
Тбайт
240 230 220 = 1048576 210 = 1024
Петабайт,
Пбайт
250 240 230 220 = 1048576
Эксабайт,
Эбайт
260 250 240 230
Зеттабайт,
Збайт
270 260 250 240
Йоттабайт,
Йбайт
280 270 260 250

6. Связь между единицами измерения
Бит
Байт
Кбайт
Мбайт
Гбайт
:8
:1024
:1024
:1024
×1024
×1024
×1024
×8

7. Определение количества
информации

8. Количество информации
Процесс познания приводит к накоплению информации (знаний), то
есть к уменьшению незнания.
Измерить объём накопленных знаний нельзя, а вот
оценить уменьшение незнания можно, если известно
количество возможных вариантов исходного состояния.

9. Подходы к измерению информации
Алфавитный
(объемный)
Содержательный
(вероятностный)
Через неопределенность
знаний с учетом вероятности
событий.
Применяется для измерения
информации, используемой
человеком.
Через количество символов с
учетом информационного веса
символа.
Применяется для измерения
информации, используемой
компьютером.
Измерение

10. Пример
Представьте, что вы зашли в магазин и попросили продать вам
жевательную резинку.
Продавщица, у которой, скажем, 16 сортов жевательной резинки,
находится в состоянии неопределенности. Она не может выполнить вашу
просьбу без получения дополнительной информации.
Если вы уточнили, скажем, - «Orbit», и из 16 первоначальных вариантов
продавщица рассматривает теперь только 8, вы уменьшили ее
неопределенность в два раза (забегая вперед, скажем, что уменьшение
неопределенности вдвое соответствует получению 1 бита
информации).
Если вы, не мудрствуя лукаво, просто указали пальцем на витрине, - «вот
эту!», то неопределенность была снята полностью.
Опять же, забегая вперед, скажем, что этим жестом в данном примере вы
сообщили продавщице 4 бита информации.
http://www.klyaksa.net/htm/kopilka/uchp/index.htm
Попова Ольга Владимировна, Информатика

11. Содержательный (вероятностный) подход
Содержательный
(вероятностный)
Через неопределенность
знаний с учетом вероятности
событий
Количество информации рассматривается
как мера уменьшения неопределенности
знания при получении информационных
сообщений.
За единицу измерения количества информации принято такое
количество информации, которое содержит сообщение, уменьшающее
неопределенность знания в два раза.
Бит (от binary digit -
двоичная цифра)

12. Формула Ральфа Хартли
N - количество возможных событий
(информационная неопределенность)
I - количество информации (количество бит
необходимых для кодирования одного события)
N = 2I
Формула позволяет определять:
Количество
событий
?Количество
информации
Количество
информации
?Количество возможных
событий

13. Задачи 1
Учитель объявляет результаты зачета:
одно из двух – «зачет», «незачет».
Сколько возможных событий может произойти?
Какова информационная неопределенность сообщения?
N = 2I
Дано:
N = 2 – количество возможных событий
I = ?
2 = 2 I  I = 1 бит – количество информации

14. Задачи 2
Учитель объявляет результаты зачета:
одно из четырех – «2», «3», «4», «5».
Сколько возможных событий может произойти?
Каково количество информации несет сообщение?
N = 2I
Дано:
N = 4 – количество возможных событий
I = ?
4 = 2 I  I = 2 бит – количество информации

15. Задачи 3
Игра крестики-нолики. Поле 8 х 8. Сколько бит необходимо для
представления информации о возможных вариантах постановки
«крестика» перед первым ходом?
N = 2I
Дано:
N = 64 – количество возможных событий
I = ?
64 = 2 I  I = 6 бит – количество информации

16. Задачи 4
Игра крестики-нолики. Поле 8 х 8. Сколько бит необходимо для
представления информации о возможных вариантах постановки
«крестика» после 35 хода?
N = 2I
Дано:
N = 64 – 35 = 29 – количество возможных событий
I = ?
2 I  29
I = 5 бит – количество информации

17. Задачи 5
Сколько бит информации получено из сообщения «Вася живёт на
пятом этаже», если в доме 16 этажей?
N = 2I
Дано
N = 16 – количество возможных событий
I = ?
I = 5 бит – количество информации

18. Задачи 6
При приёме некоторого сообщения получили 7 бит информации.
Сколько вариантов исхода было до получения сообщения?
N = 2I
Дано
I = 7 – количество информации
N = ?
N = 27 – количество возможных событий
N = 128

19. Задачи на дом
1. Шарик находится в одной из 32 урн. Сколько единиц информации
будет содержать сообщение о том, где он находится?
2. После реализации одного из возможных событий получили
количество информации равное 15 бит. Какое количество
возможных событий было первоначально?
3. При угадывании целого числа в диапазоне от 1 до N было
получено 10 битов информации. Чему равно N?

20. Алфавитный (объёмный) подход
При определении количества информации,
отвлекаются от содержания информации и
рассматривают информационное сообщение
как последовательность символов
определенной знаковой системы.
Объем информации связан с общим числом символов и «мощностью»
алфавита («информационная емкость» символа) и не учитывает
содержание сообщения.
Алфавитный
(объемный)
Через количество символов с
учетом информационного веса
символа

21. Определение количества
текстовой информации

22. Формула Ральфа Хартли
N – мощность алфавита (количество знаков в
алфавите)
I – информационная ёмкость символа (количество
информации, которое несет один знак)
N = 2I
Мощность русского алфавита – 33 знака
Информационная емкость буквы в русском алфавите
составляет:
2 I  33, т.е. I = 6 бит

23. Количество информации в сообщении
P – количество информации в сообщении
I – информационная ёмкость символа
(количество информации, которое несет
один знак)
K – длина сообщения
Примечание
Знаки несут одинаковое количество информации.
P = IK

24. Задачи 6
Алфавит племени Мумбо-Юмбо составляет 6 символов. Сколько
битов информации содержится в слове длиной в 12 символов.
N = 2I
Дано:
N = 6 – мощность алфавита
K = 12 символов – длина сообщения
P - ?
2 I  6
I = 3 бита – информационная ёмкость символа
P = IK
P = 3  12 = 36 бит – количество
информации в сообщении

25. Задачи на дом
1. Объем сообщения равен 300 бит. Сообщение содержит 50
символов. Какова мощность алфавита?
2. Для кодирования секретного сообщения используются 12
специальных значков-символов. При этом символы кодируются
одним и тем же минимально возможным количеством бит. Чему
равен информационный объем сообщения длиной в 256 символов?

26. Определение количества
графической информации

27. Формула Ральфа Хартли
N – количество цветов (палитра)
I – глубина цвета (количество информации,
которое несет один цвет)
N = 2I
Палитра содержит 60 цветов.
Глубина цвета этой палитры составляет:
2 I  60, т.е. I = 6 бит

28. Объём изображения
P – объём изображения
I – глубина цвета в битах
M × L – разрешение изображения (в пикселях)
P = IML
L
M

29. Задачи 6
Изображение размером 640х320 пикселей представлено 128
цветной палитрой. Каков объём этого изображения?
N = 2I
Дано:
N = 128 – цветов в палитре
M×L = 640×320 пикселей – разрешение
P - ?
2 I  128
I = 7 битов – глубина цвета
P = IML P = 7  640  320 = 1433600 бит = 175 Кбайт

30. Объём видеопамяти
P – объём видеопамяти
I – глубина цвета в битах
M×L – разрешение монитора (в пикселях)
C – количество видеостраниц
P = IMLС
L
M

31. Определение количества
звуковой информации

32. Формула Ральфа Хартли
N – количество уровней звукового сигнала
I – глубина звука (информационная ёмкость)
N = 2I

33. © Ю.А. Чиркин МОУ СОШ №19 г. Мичуринск, 2009-2010Расчёт объёма звукового файла
P – размер (объём) звукового файла
(в битах)
I – глубина кодирования (в битах)
V – частота дискретизации (в Герцах)
C – количество дорожек в записи
(C=1 – моно, C=2 – стерео)
T – время звучания (в секундах)
P = IVCT

34. Задачи 7
Дано:
I = 16 бит
V = 44,1 КГц
T = 3 мин 18 сек
С = 2
P - ?
44,1 КГц = 44100 Гц
3 мин 18 с = 198 сек
P = IV C T = 2·44100 Гц·16 бит·198 сек =
= 279417600 бит = 34927200 байт ≈ 34108,6 Кб
≈ 33,3 Мб
P = IVCT
Определить объём звукового стерео файла записанного
разрядностью 16 бит с частотой дискретизации 44,1 КГц, если
время его звучания составляет 3 мин 18 сек.

35. Подходы к измерению информации
Алфавитный
(объемный)
Содержательный
(вероятностный)
Через неопределенность
знаний с учетом вероятности
событий
Через количество символов с
учетом информационного веса
символа
Измерение
Количество информации
(I)
Информационная емкость символа, глубина
цвета, глубина звука (I)
N = 2 I N = 2 I
Количество возможных
событий (N)
Мощность алфавита, палитра, количество
уровней звукового сигнала (N)
N = 2 I N = 2 I
Количество информации (P)
P = IK P = IMLC P = IVCT