Download to read offline
Uploaded bydavidovanat
симметрия в физике
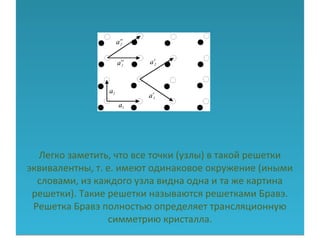
Документ посвящен исследованию роли симметрии в различных областях науки, включая физику, математику, химию и биологию. Ученики 11 класса представляют гипотезу о существовании физических процессов, обладающих симметрией, и систематизируют знания по этой теме, рассматривая историю и примеры симметрии в кристаллах. Основное внимание уделяется трансляционной и точечной симметрии кристаллических решеток, включая решетки Браве.
симметрия в физике
- 1. Проект Симметрия в физике Выполнилиученики 11класса Молоткова Олеся, Ермошина Юлия, Мартьянов Михаил 2010
- 2. Актуальность Понятие симметриипроходит через всю многовековую историю человеческогоПонятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широкотворчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки.используют все без исключения направления современной науки. Принципы симметрии играют важную роль в физике и математике, химии иПринципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыкебиологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке В понятие симметрия заложен глубинный смысл. Симметрия буквальноВ понятие симметрия заложен глубинный смысл. Симметрия буквально пронизывает весь окружающий нас мир.пронизывает весь окружающий нас мир.
- 3. Гипотеза Существуют физические процессыобладающие симметрией.
- 4. Цель Показать роль симметриив физических процессах
- 5. Задачи Систематизировать знания осимметрии Показать роль симметрии в физике
- 6. Ход исследования Изучитьлитературу по данной теме Выяснить историю возникновения симметрии Рассмотреть физические процессы обладающие симметрией Опровергнуть или доказать гипотезу
- 8.
- 16. Силовые линии магнитногополя землиСиловые линии магнитного поля земли
- 26. Трансляционная симметрия кристалла Наиболееважной датой в истории физики твердого тела считается 1912 г., когда Лауэ доказал посредством дифракции рентгеновских лучей, что кристаллы состоят из периодических рядов атомов. Под упорядоченным расположением атомов в кристалле подразумевается его пространственная периодичность. Иными словами, для каждого кристалла можно выбрать три вектора а1, а2, а3, не лежащих в одной плоскости, таких, что при смещении кристалла как целого на любой из этих векторов, он совмещается сам с собой. Операция перемещения кристалла на вектор , где n1, n2, n3 — целые числа, называется трансляцией. Говорят, что кристалл обладает трансляционной симметрией, т. к. при трансляции на вектор он совмещается сам с собой. Трансляционная симметрия кристалла Наиболее важной датой в истории физики твердого тела считается 1912 г., когда Лауэ доказал посредством дифракции рентгеновских лучей, что кристаллы состоят из периодических рядов атомов. Под упорядоченным расположением атомов в кристалле подразумевается его пространственная периодичность. Иными словами, для каждого кристалла можно выбрать три вектора а1, а2, а3, не лежащих в одной плоскости, таких, что при смещении кристалла как целого на любой из этих векторов, он совмещается сам с собой. Операция перемещения кристалла на вектор , где n1, n2, n3 — целые числа, называется трансляцией. Говорят, что кристалл обладает трансляционной симметрией, т. к. при трансляции на вектор он совмещается сам с собой.
- 27. Легко заметить, чтовсе точки (узлы) в такой решетки эквивалентны, т. е. имеют одинаковое окружение (иными словами, из каждого узла видна одна и та же картина решетки). Такие решетки называются решетками Бравэ. Решетка Бравэ полностью определяет трансляционную симметрию кристалла. Легко заметить, что все точки (узлы) в такой решетки эквивалентны, т. е. имеют одинаковое окружение (иными словами, из каждого узла видна одна и та же картина решетки). Такие решетки называются решетками Бравэ. Решетка Бравэ полностью определяет трансляционную симметрию кристалла.
- 28. Для кубических кристалловсуществуют 3 типа решеток Бравэ: Простая кубическая решетка (очень редко встречается). Кубическая гранецентрированная решетка, ГЦК. В центре каждой грани находится еще по одному атому Объемоцентрированная кубическая решетка, ОЦК. Дополнительный атом помещен в центр куба Для кубических кристаллов существуют 3 типа решеток Бравэ: Простая кубическая решетка (очень редко встречается). Кубическая гранецентрированная решетка, ГЦК. В центре каждой грани находится еще по одному атому Объемоцентрированная кубическая решетка, ОЦК. Дополнительный атом помещен в центр куба
- 29. Решетка Бравэ отражаеттрансляционную структуру (симметрию) кристалла, а не его кристаллическое строение. Кроме трансляционной, кристаллы обладают точечной симметрией: симметрией по отношению к поворотам и отражениям. Точечная симметрия кристаллов. Точечное преобразование в теории симметрии – это преобразование, которое оставляет в покое, т. е. неподвижной, хотя бы одну точку фигуры. Если при некотором точечном преобразовании фигура переходит сама в себя, то говорят, что она симметрична относительно этого преобразования (обладает соответствующим элементом симметрии: осью, плоскостью отражения и т. д.) Решетка Бравэ отражает трансляционную структуру (симметрию) кристалла, а не его кристаллическое строение. Кроме трансляционной, кристаллы обладают точечной симметрией: симметрией по отношению к поворотам и отражениям. Точечная симметрия кристаллов. Точечное преобразование в теории симметрии – это преобразование, которое оставляет в покое, т. е. неподвижной, хотя бы одну точку фигуры. Если при некотором точечном преобразовании фигура переходит сама в себя, то говорят, что она симметрична относительно этого преобразования (обладает соответствующим элементом симметрии: осью, плоскостью отражения и т. д.)
- 32. Выводы • Симметрия вфизических процессах существует
- 33. Информационные источники • http:// e - sciense.ru/phisics/ theory • http: // ref. byfrefs/88/index.html • http: // nova.ramfler.ru/pictures