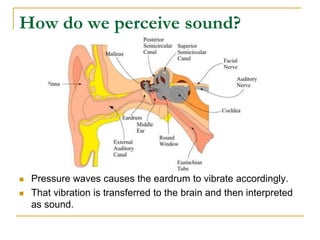
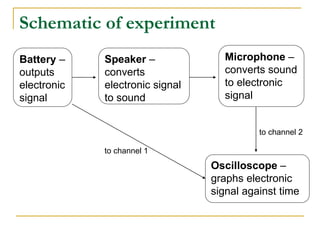
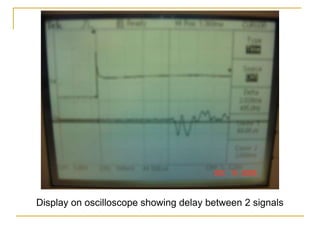
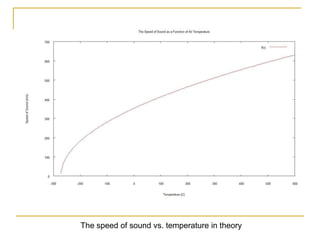
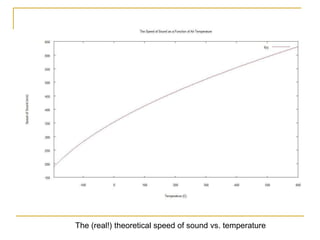
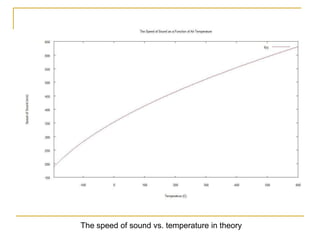
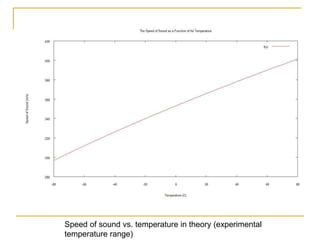
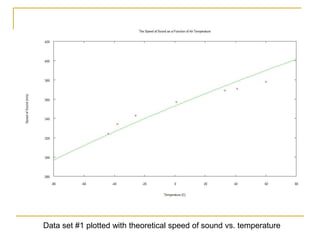
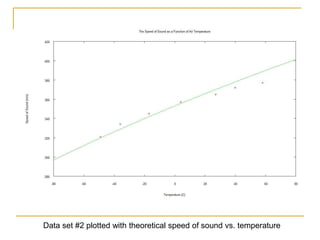
This document describes an experiment to investigate how the speed of sound varies with temperature in air. The experiment involves using a speaker and microphone to measure the time delay of a sound wave traveling through air at different temperatures, controlled by cooling with liquid nitrogen and heating with lamps. The results are analyzed and found to closely match the theoretical prediction from statistical mechanics that the speed of sound increases with temperature according to the given equation. Sources of experimental error are also discussed.

1. Investigating the
Properties of Sound
Demonstrating the temperature
dependence of the speed of sound in air

2. Outline
 Introduction to sound waves
 The experiment – measuring the temperature
dependence of the speed of sound
 The theory of sound propagation
 Data analysis and discussion of
experimental results
 Conclusion

3. What is sound in physics terms?
 A longitudinal travelling wave.
 Caused by an oscillation of pressure (the
compression and dilation of particles) in matter.
 Other names for sound are pressure waves,
compression waves, and density waves.
 Names derived from the motion of particles that carry
sound.
Sound wave animation:
http://paws.kettering.edu/~drussell/Demos/waves/wavemotion.html
Notice that each individual particle merely oscillates.

4. How do we perceive sound?
 Pressure waves causes the eardrum to vibrate accordingly.
 That vibration is transferred to the brain and then interpreted
as sound.

5. Some properties of sound
 Volume
 Amplitude of sound wave – how large are the
particle displacements?
 Pitch
 Frequency of oscillations.
 Speed of propagation
 How fast does a sound wave travel?
 What factors affect the speed of sound?

6. The experiment
 Purpose
 To determine how the speed of sound is
dependent on the temperature of the medium.
 Motivation for this study
 Musicians: try playing an (accurately tuned)
instrument in the freezing cold; the intonation will
be completely off.
 Effect is most apparent with brass instruments.
 Then warm the instrument up again without
retuning, the intonation is fine again. Why?

7. Schematic of experiment
Speaker –
converts
electronic signal
to sound
Microphone –
converts sound
to electronic
signal
Oscilloscope –
graphs electronic
signal against time
Battery –
outputs
electronic
signal
to channel 1
to channel 2

8. Display on oscilloscope showing delay between 2 signals

9. Apparatus
 Large Styrofoam cooler
 Liquid nitrogen
 Heating lamps (60W)
 Digital thermometer
 Two-channel digital oscilloscope
 Speaker
 Microphone
 Battery (9V) with switch

10. Entire experimental setup (outside view)

11. Inside the cooler

12. Boiling liquid nitrogen inside cooler

13. Halogen heating lamp

14. Fan to promote air circulation

15. Digital thermometer

16. Battery (inside box) with switch and signal splitter

17. Speaker

18. Microphone

19. Digital oscilloscope

20. Entire experimental setup again

21. Collecting the data
 Cooler has already been cooled with liquid
nitrogen to approx. -60˚C.
 We will periodically pause the lecture and
take a data point.
 Turn on battery to send a voltage pulse.
 This pulse triggers the oscilloscope to (1) start
reading and (2) freeze graph on screen (pre-set
oscilloscope functions).
 Immediately record the temperature.
 Use oscilloscope cursors to measure the time
delay between the signals on channels 1 and 2.

22. How is sound modeled mathematically?
 Sound is a somewhat abstract concept
 A sound wave isn’t an object – it’s a type of
particle motion.
 That motion can be understood as travelling
compressions and rarefactions in a medium.
 Most straight-forward method to describe
sound is to keep track of the positions of
every particle that mediates the sound wave.
 Number of particles is on the order of 1023 –
impossible to calculate the movement of
every single particle!

23.  Real method:
 Same idea, but no need to keep track of every
particle individually.
 Use probability and statistics to “guess” the
collective behaviour of particles.
 The branch of physics that uses statistics to
model very large systems is called
thermodynamics, or statistical mechanics.
 Sound is a statistical mechanical
phenomenon.

24. Important Definitions
 Bulk modulus (K)
 A measure of the elasticity of a gas; ie. how easily is the
gas compressed?
 Analogous to the spring constant in Hooke’s law
V
P
V
K



x
k
F 


V
V
K
P



Just as a high spring constant
corresponds to a stiffer spring, a
high bulk modulus corresponds to a
less compressible gas – a “stiffer”
gas.
P
K 
 
For diatomic gases

25.  Adiabatic process
 A physical process in which heat does not enter or
leave the system.
 The compression and dilation of air to form a
sound wave is an adiabatic process.
 Adiabatic index (γ)
 A thermodynamic quantity related to the specific
heat capacities of substances.
 Here γ accounts for the heat energy associated
with compression, which adds to the gas
pressure.
 γ ≈ 1.4 for diatomic gases.

26. The speed of sound in theory
 A rigorous derivation of the speed of sound from first
principles in statistical mechanics is much too
complicated.
 We need to start somewhere though, so lets begin
with a more easily accessible equation.

K
c 


P

The speed of sound is denoted as c by
convention; p is pressure and ρ is density.
So where’s the dependence on temperature?

27. Recall from chemistry class the ideal gas law:
T
Nk
PV B
 where P is pressure, V is volume,
N is the number of particles, kB is
the Boltzmann constant, and T is
temperature in Kelvin.
V
T
k
N
c B







Substituting for P in our previous expression:
Now realize:
M
V 


m
N
V



Therefore where m is the mass of a
single molecule.

28. m
T
k
c B 



Substituting in m gives us:
15
.
273
1
15
.
273

 




m
kB
 is temperature in Celsius.
Now realize T = + 273.15, where 
15
.
273


 

m
k
c B
Therefore
15
.
273
1
353



nitrogen
c ms-1
Notice that the first term is equal to the speed of sound at 0˚C.
Lastly, substitute in the correct numerical values and simplify to get:
Why do we want the expression specifically for nitrogen gas?

29. The speed of sound vs. temperature in theory

30. The (real!) theoretical speed of sound vs. temperature

31. Analyzing our data
 Our raw data gives us, at each temperature,
the travel time Δt of the sound wave.
 To extract speed, divide the distance
between the speaker and microphone by Δt.
 Distance measured to be 73cm.
 Now we can graph the speed of sound
against temperature.
 See how closely our data matches up with
theoretical predictions.

32. The speed of sound vs. temperature in theory

33. Speed of sound vs. temperature in theory (experimental
temperature range)

34. Data set #1 plotted with theoretical speed of sound vs. temperature

35. Data set #2 plotted with theoretical speed of sound vs. temperature

36. Discussion of experimental errors
 Many sources of measurement uncertainty.
 Distance between speaker and microphone.
 Uneven temperature distribution inside cooler.
 Air leakage – escaping nitrogen replaced by normal air.
 Oscilloscope screen does not clearly define the beginning
of the microphone signal.
 Acoustic noise from sounds inside room.
 Electronic noise from battery, microphone, etc.
 The approximations made in the derivation of the speed of
sound:
P
K 
  and 4
.
1



37. In summary
 What we perceive as sound is actually oscillations
of air particles.
 These oscillations are caused by pressure waves
travelling through the air.
 Sound waves are mathematically described by
statistical mechanics.
 The speed of sound is dependent on the
temperature of the medium carrying it, and obeys
the equation:
T
m
k
K
c B





