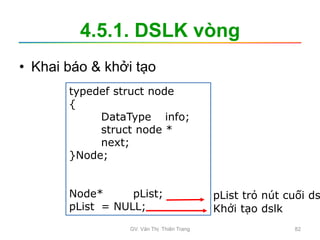
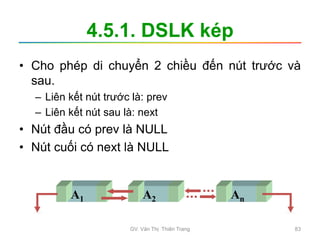
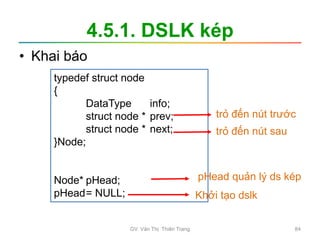
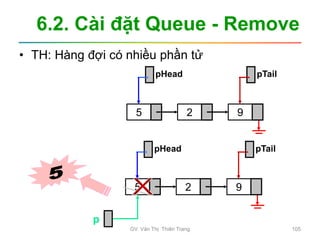
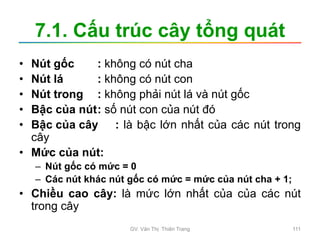
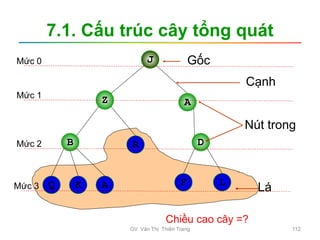
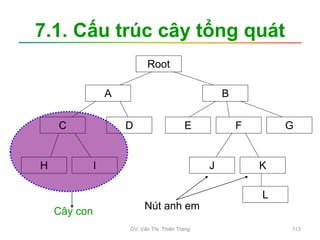
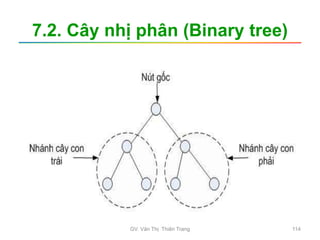
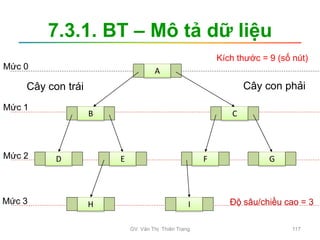
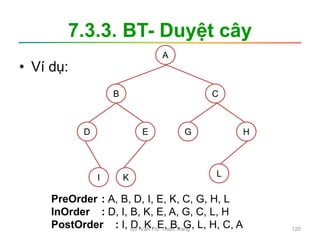
Tài liệu trình bày nội dung học phần về cấu trúc dữ liệu và giải thuật, nhằm giúp sinh viên hiểu tầm quan trọng của giải thuật và cách tổ chức dữ liệu trong lập trình. Các chủ đề bao gồm tìm kiếm, sắp xếp, và các cấu trúc dữ liệu cơ bản như danh sách, stack, queue, và cây nhị phân. Học viên cũng được khuyến khích phát triển kỹ năng lập trình thông qua các bài tập thực hành.
















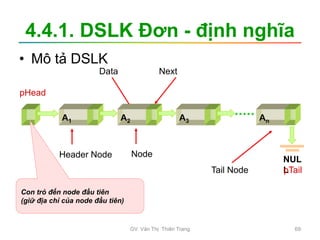
![2.1. Giới thiệu bài toán tìm kiếm
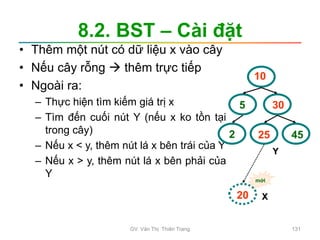
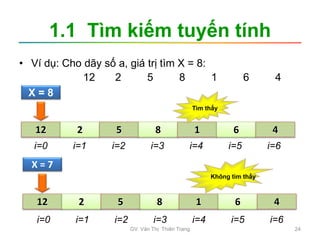
• Bài toán được mô tả như sau:
– Tập dữ liệu được lưu trữ là dãy a1, a2,..,an. Giả sử
chọn cấu trúc dữ liệu mảng để lưu trữ dãy số này
trong bộ nhớ chính, có khai báo: int a[n];
– Khóa cần tìm là x: int x;
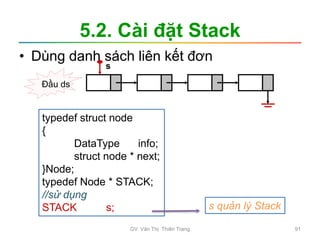
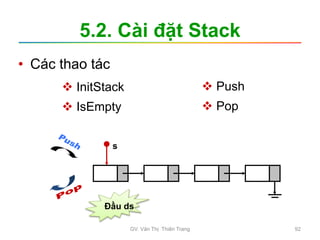
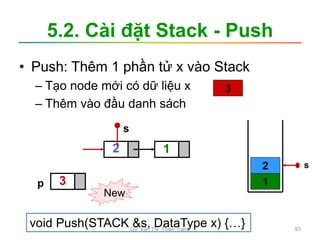
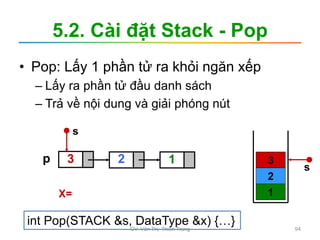
Tìm kiếm
Tìm kiếm tuyến tính Tìm kiếm nhị phân
Tập dữ liệu đã
được sắp xếp
Tập dữ liệu
bất kỳ
GV. Văn Thị Thiên Trang 22](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-22-320.jpg)
![2.1. Giới thiệu bài toán tìm kiếm
• Ý tưởng: duyệt tuần tự từ phần tử đầu tiên, lần lượt so
sánh khóa tìm kiếm với khoá tương ứng của các phần
tử trong danh sách. Cho đến khi gặp phần tử cần tìm
hoặc đến khi duyệt hết danh sách.
• Các bước tiến hành như sau:
i = 0
a[i] = x
i = i + 1
i<n Không tìm thấy
Tìm thấy
Đ
Đ
S
S
GV. Văn Thị Thiên Trang 23](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-23-320.jpg)
![1.1 Tìm kiếm tuyến tính
• Thuật toán tìm kiếm tuyến tính
/* Trả về: vị trí xuất hiện đầu tiên của x trong mảng a
Trả về: -1 nếu x không có trong mảng a */
int Search(int a[], int n, int key)
{
int i =0;
while (i<n && key != a[i])
i++;
if (i < n)
return i; // tìm thấy tại vị trí i
return -1; // tìm không thấy
}
GV. Văn Thị Thiên Trang 25](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-25-320.jpg)
![1.1 Tìm kiếm tuyến tính
• Thuật toán tìm kiếm tuyến tính cải tiến
int Search(int a[], int n, int key)
{
int i =0;
a[n] =key; // thêm phần tử thứ n+1
while (key != a[i])
i++;
if (i == n)
return -1; // tìm hết mảng nhưng không có x
return i; // tìm thấy x tại vị trí i
}
GV. Văn Thị Thiên Trang 26](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-26-320.jpg)

![1.2 Tìm kiếm nhị phân
• Phép tìm kiếm nhị phân được áp dụng
trên dãy khóa đã có thứ tự: k[1] k[2] ...
k[n].
GV. Văn Thị Thiên Trang 28](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-28-320.jpg)
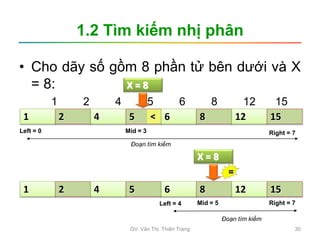
![1.2 Tìm kiếm nhị phân
• Giả sử ta cần tìm trong đoạn a[left,..,right] với khóa tìm kiếm
là X
• Chia đôi phạm vi tìm kiếm mid=(left+right)/2.
• Xét phần tử giữa là a[mid]:
– Nếu a[mid]=X: Tìm thấy tại vị trí mid.
– Nếu a[mid]<X:
• Đoạn a[left,..,mid] chứa các phần tử <X
• Tìm X trong đoạn a[mid+1,.., right]
– Nếu a[mid]>X:
• Đoạn a[mid,..,right] chứa các phần tử >X
• Tìm X trong đoạn a[left,.., right-1]
• Quá trình tìm kiếm thất bại nếu left>right
GV. Văn Thị Thiên Trang 29](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-29-320.jpg)
![1.2 Tìm kiếm nhị phân
int BinarySearch(int a[], int n, int key){
int left = 0, right = n-1, mid;
while (left <= right){
mid = (left + right)/ 2; // lấy điểm giữa
if (a[mid] == key) // nếu tìm được
return mid;
if (a[mid] < key) // tìm đoạn bên phải mid
left = mid+1;
else
right = mid-1; // tìm đoạn bên trái mid
}
return -1; // không tìm được
}
GV. Văn Thị Thiên Trang 31](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-31-320.jpg)
![CÂU HỎI ÔN TẬP BÀI 2
1. Sinh mảng ngẫu nhiên gồm N số nguyên có giá trị (-
100, 100)
– Tìm phần tử có giá trị X trong mảng bằng 2 phương pháp: Tìm
tuần tự và tìm nhị phân
2. Cho cấu trúc Sách (Mã sách: char[10], Tên sách:
char[40], Giá: long). Viết chương trình thực hiện:
– Nhập, xuất danh sách gồm N cuốn sách.
– Tìm cuốn sách có mã là X bằng phương pháp tìm kiếm tuần tự
(X nhập từ bàn phím).
– Tìm cuốn sách có mã là X bằng phương pháp tìm kiếm nhị
phân. (X nhập từ bàn phím).
– Liệt kê thông tin các cuốn sách có giá > G (G nhập từ bàn phím).
– Tìm cuốn sách có giá lớn nhất.
GV. Văn Thị Thiên Trang 32](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-32-320.jpg)





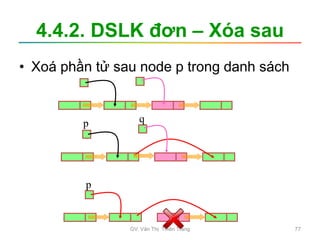
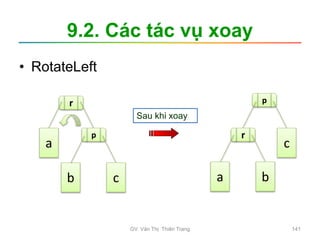
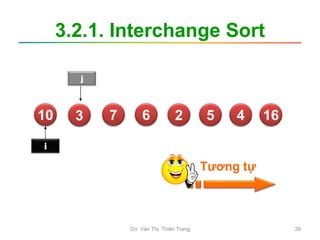
![3.2.1. Interchange Sort
• Các bước tiến hành
B1: i = 0; // bắt đầu từ đầu dãy
B2: j = i +1; // duyệt qua các phần tử sau
B3: Chừng nào j < n thực hiện:
Nếu a[j] < a[i] thì Đổi chỗ a[i] và a[j];
j = j +1;
B4: i = i +1;
Nếu i<n-1 thì lặp lại B2;
Ngoài ra Kết thúc!
GV. Văn Thị Thiên Trang 38](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-38-320.jpg)

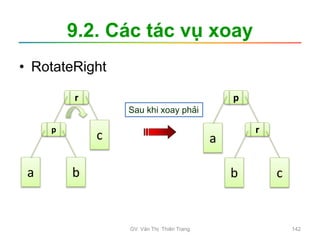
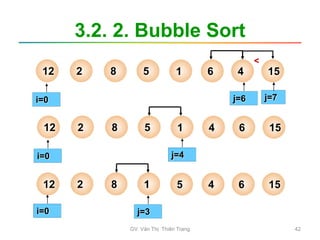
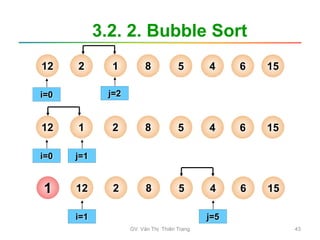
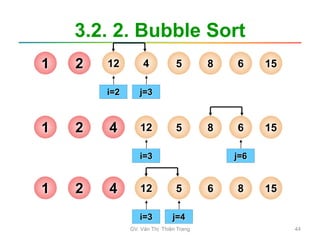
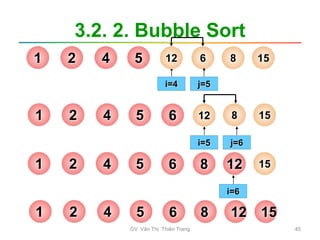
![3.2. 2. Bubble Sort
• Các bước tiến hành
– B1: i=0; // lần xử lý đầu tiên
– B2: j=n-1; // duyệt từ cuối dãy ngược về vị
trí i
Trong khi (j>i) thực hiện:
Nếu a[j] < a[j-1]: Hoán đổi a[j] và a[j-1]
j = j -1;
– B3: i = i+1; // lần xử lý kế tiếp
Nếu i > n-2: Hết dãy Dừng
Ngược lại: quay lại B2
GV. Văn Thị Thiên Trang 41](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-41-320.jpg)
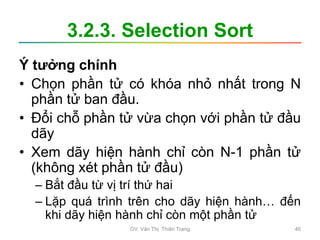
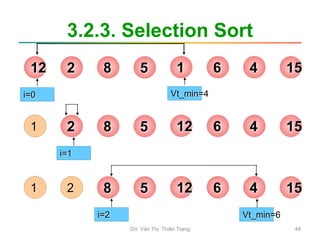
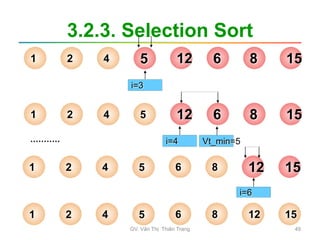
![3.2.3. Selection Sort
• Các bước thực hiện:
–B1: i = 0
–B2: Tìm phần tử a[min] nhỏ nhất trong
dãy hiện hành từ a[i] đến a[n-1]
–B3: Hoán vị a[i] và a[min]
–B4: Nếu i < n -2 thì i = i+1 Lặp B2
Ngược lại Dừng
GV. Văn Thị Thiên Trang 47](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-47-320.jpg)
![3.2.4. Insertion Sort
• Ý tưởng chính
– Cho dãy ban đầu a[0], a[1],.., a[n-1], ta có thể xem
dãy con gồm một phần tử a[0] đã được sắp.
– Sau đó thêm a[1] vào đoạn a[0] sao cho a[0] a[1]
được sắp.
– Tiếp tục thêm a[2] vào để có a[0] a[1] a[2] được
sắp....
– Cho đến khi thêm xong a[n-1]
vào đoạn a[0] a[1]...a[n-2]
đoạn a[0] a[1]...a[n-2] a[n-1]
được sắp.
GV. Văn Thị Thiên Trang 50](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-50-320.jpg)
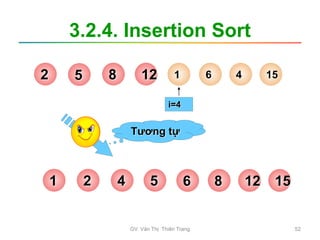
![3.2.4. Insertion Sort
• Các bước tiến hành
– B1: i = 1; //giả sử có đoạn a[0] đã được
sắp
– B2: x= a[i];
Tìm được vị trí cần chèn x vào là pos
– B3: Dời chỗ các phần tử từ a[pos] a[i-1]
sang phải một vị trí để dành chỗ cho a[i].
– B4: a[pos] = x; // có đoạn a[0]...a[i] được sắp.
– B5: i = i +1;
Nếu i < n: Lặp lại B2
Ngược lại: Dừng Dãy đã được sắp
GV. Văn Thị Thiên Trang 51](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-51-320.jpg)
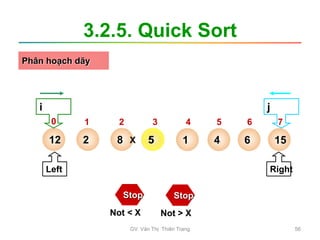
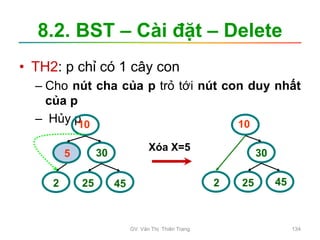
![3.2.5. Quick Sort
• huật toán do Hoare đề xuất
– Tốc độ trung bình nhanh hơn thuật toán khác
– Do đó Hoare dùng “quick” để đặt tên
• Ý tưởng chính
– QS phân hoạch dãy ban đầu thành hai phần
dựa vào một giá trị x
• Dãy 1: gồm các phần tử a[i] ko lớn hơn x (<=x)
• Dãy 2: gồm các phần tử a[i] ko nhỏ hơn x (>=x)
GV. Văn Thị Thiên Trang 53](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-53-320.jpg)
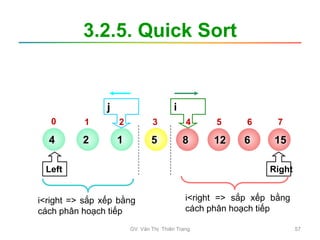
![3.2.5. Quick Sort
• Giải thuật sắp xếp dãy a[left],
a[left+1],...,a[right] được phát biểu đệ quy
như sau:
• B1: Phân hoạch dãy a[left]...a[right] thành các
dãy con:
– Dãy con 1: a[left]...a[j] < x
– Dãy con 2: a[j+1]...a[i-1] = x
– Dãy con 3: a[i]...a[right] > x
• B2:
– Nếu (left < j) // dãy con 1 có nhiều hơn 1 phần tử
Phân hoạch dãy a[left]...a[j]
– Nếu (i < right) // dãy con 3 có nhiều hơn 1 phần tử
Phân hoạch dãy a[i]...a[right]
GV. Văn Thị Thiên Trang 54](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-54-320.jpg)
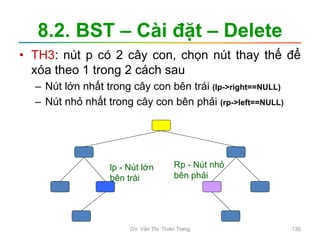
![3.2.5. Quick Sort
• Sau khi phân hoạch thì dãy ban đầu được phân thành ba
phần:
– a[k] < x, với k = 1...i
– a[k] = x, với k = i..j
– a[k] > x, với k = j..n
• Nếu đoạn 1, đoạn 3 đều có 1 phần tử thì dãy ban đầu được
sắp
• Nếu đoạn 1 hoặc đoạn 3 có nhiều hơn 1 phần tử thì ta cần
sắp lại đoạn đó (áp dụng phân hoạch như trên)
a[k] < x a[k] = x a[k] > x
GV. Văn Thị Thiên Trang 55](https://image.slidesharecdn.com/slidecautrucdlgt-230419084357-76d1dc11/85/SLIDE-CAU-TRUC-DL_GT-pptx-55-320.jpg)