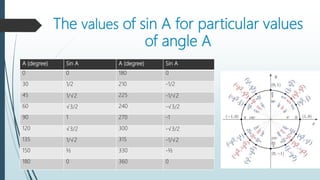
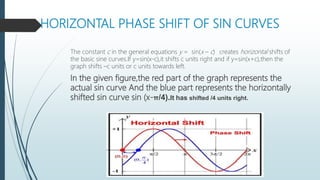
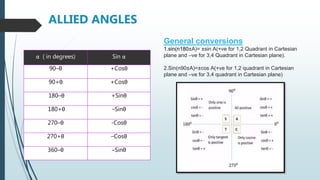
The document discusses the basic properties and transformations of the sine curve. It defines sine as the ratio of the opposite side to the hypotenuse in a right triangle. The sine curve has a period of 2π and is an odd function. The domain is all real numbers and the range is [-1,1]. Horizontal phase shifts move the sine curve left or right. Allied angles use trigonometric identities to relate sine and cosine values for angles in all four quadrants. Examples demonstrate finding sine values for specific angles. Vertical shifts, amplitude changes, and absolute value functions are shown to transform the basic sine curve. Applications of trigonometry include astronomy, construction, and satellite navigation.

1. Sine curve and its
transformations
Sandeepan Narayan Behera
Class-XI,
Section- E

2. BASIC PROPERTIES OF SINE FUNCTION
 Sine is a trigonometric function. It is defined as p/h in a right angle triangle, where p is the
perpendicular and h is the hypotenuse.In triangle ABC,sin A=BC/AB.
 Sin A is a periodic function, with period 2 π
 Sin A is an odd function. Sin (-A)= -Sin A
 Domain of Sin x : ( -∞ , +∞ )
 Range of Sin x : [ -1 , 1 ]

3. GRAPH OF SINX
If, sin θ = sin α
Then, General Solution of sine function :
θ = nπ + (-1)
n
α, where α ∈ [-π/2, π/2]

4. The values of sin A for particular values
of angle A
A (degree) Sin A A (degree) Sin A
0 0 180 0
30 1/2 210 -1/2
45 1/√2 225 -1/√2
60 √3/2 240 -√3/2
90 1 270 -1
120 √3/2 300 -√3/2
135 1/√2 315 -1/√2
150 ½ 330 -½
180 0 360 0

5. HORIZONTAL PHASE SHIFT OF SIN CURVES
The constant c in the general equations y = sin(x – c) creates horizontal shifts of
the basic sine curves.If y=sin(x-c),it shifts c units right and if y=sin(x+c),then the
graph shifts –c units or c units towards left.
In the given figure,the red part of the graph represents the
actual sin curve And the blue part represents the horizontally
shifted sin curve sin (x-π/4).It has shifted /4 units right.

6. ALLIED ANGLES
α ( in degrees) Sin α
90–θ +Cosθ
90+θ +Cosθ
180–θ +Sinθ
180+θ –Sinθ
270–θ -Cosθ
270+θ –Cosθ
360–θ –Sinθ
General conversions
1.sin(n180±A)= ±sin A(+ve for 1,2 Quadrant in Cartesian
plane and –ve for 3,4 Quadrant in Cartesian plane).
2.Sin(n90±A)=±cos A(+ve for 1,2 quadrant in Cartesian
plane and –ve for 3,4 quadrant in Cartesian plane)

7. EXAMPLES BASED ON THE ABOVE
CONCEPTS
Example 1- Find the value of sin 225°
Solution-
sin(180+45)=-sin 45 °(Since , if something is added to or subtracted to 180 °,then sin function doesn’t
change only sign of sine function changes).
-Sin 45= -1/√2
Example 2- Find the value of sin 150°
Solution-
Sin(90 + 60) = +cos 60° ( Since 150° lies in the second quadrant)
Sin 150° = cos 60° = 1/2

8. Vertical shift of sine curve
If , y= a + sin x, then the curve shifts upwards by a unit and if , y= a- sinx , then curve shifts
downwards by –a units
Other forms are y= - a + sinx , y= -a - sinx

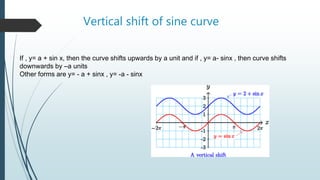
9. Sine curve with f(x)= k sin x transformation
Y= a sin x form changes the amplitude of sin x to from 1 to k.The
range of ksinx is [-k,k].The crest and trough changes as k times -1
or 1

10. .Graph of y = Isin xI
.Graph of y = sin |x|

11. Trigonometric product and sum formulae
Product to sum
Sum to Product

12. EXAMPLES
Question :
Answer :

13. APPLICATIONS
 Astronomy :
It helps in determining the distance between the stars and planets. The tables
help in locating the position of a sphere and this kind of trigonometry is called
spherical trigonometry.
 Construction :
Trigonometry is used in construction sites in measuring ground surfaces and
fields. When constructing a building, aspects like roof inclination, rook slopes,
perpendicular and parallel walls, light angles, sun shading, etc, require
trigonometry.
 Satellite Navigation System :
The satellite navigation system also uses trigonometric functions such as the
law of cosine to calculate simple equations to help in locating the satellites in
the earth's orbit 24 hours.

14. QUESTIONS FOR THE AUDIENCE
1.
2.
3.

15. THANK YOU