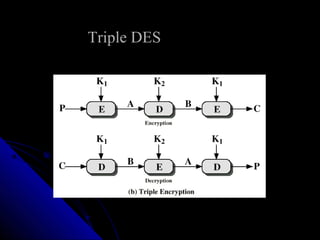
This document provides an overview of symmetric and asymmetric cryptography. Symmetric cryptography uses the same key for encryption and decryption, while asymmetric cryptography uses different keys. The Merkle-Hellman knapsack cryptosystem was one of the earliest public key systems, but it was broken. The RSA algorithm uses a public/private key pair to encrypt and decrypt messages securely. DES was developed as a standard for encrypting sensitive data.













![Merkle-Hellman KnapsackMerkle-Hellman Knapsack
Example (Encrypt Process)
Given S = {1, 2, 4, 9} (private key) and H = {15,
13, 9, 16} (public key) with w = 15, n = 17 and m
= 4 (divide the block into m bits). Message is
0100 1011 1010 0101.
With H = {15, 13, 9, 16} the message is encoded
as follows:
[0 1 0 0] * [15, 13, 9, 16] = 13
[1 0 1 1] * [15, 13, 9, 16] = 40
[1 0 1 0] * [15, 13, 9, 16] = 24
[0 1 0 1] * [15, 13, 9, 16] = 29](https://image.slidesharecdn.com/3chapter3secureencyrptionsystemslatest-130716022439-phpapp02/85/Secure-Encyrption-Systems-Chapter-2-14-320.jpg)
![Merkle-Hellman KnapsackMerkle-Hellman Knapsack
Example Decryption Process
To decrypt, we first need to find the inverse of
15 mod 17 and this is equal to 8. Multiply all the
encrypted message C with 8 mod 17 to get the
sum si.
Note :
S = {1, 2, 4, 9} (private key)
13 * 8 mod 17 = 2 = [0100]
40 * 8 mod 17 = 14 = [1011]
24 * 8 mod 17 = 5 = [1010]
29 * 8 mod 17 = 11 = [0101]
The recovered message is 0100101110100101](https://image.slidesharecdn.com/3chapter3secureencyrptionsystemslatest-130716022439-phpapp02/85/Secure-Encyrption-Systems-Chapter-2-15-320.jpg)