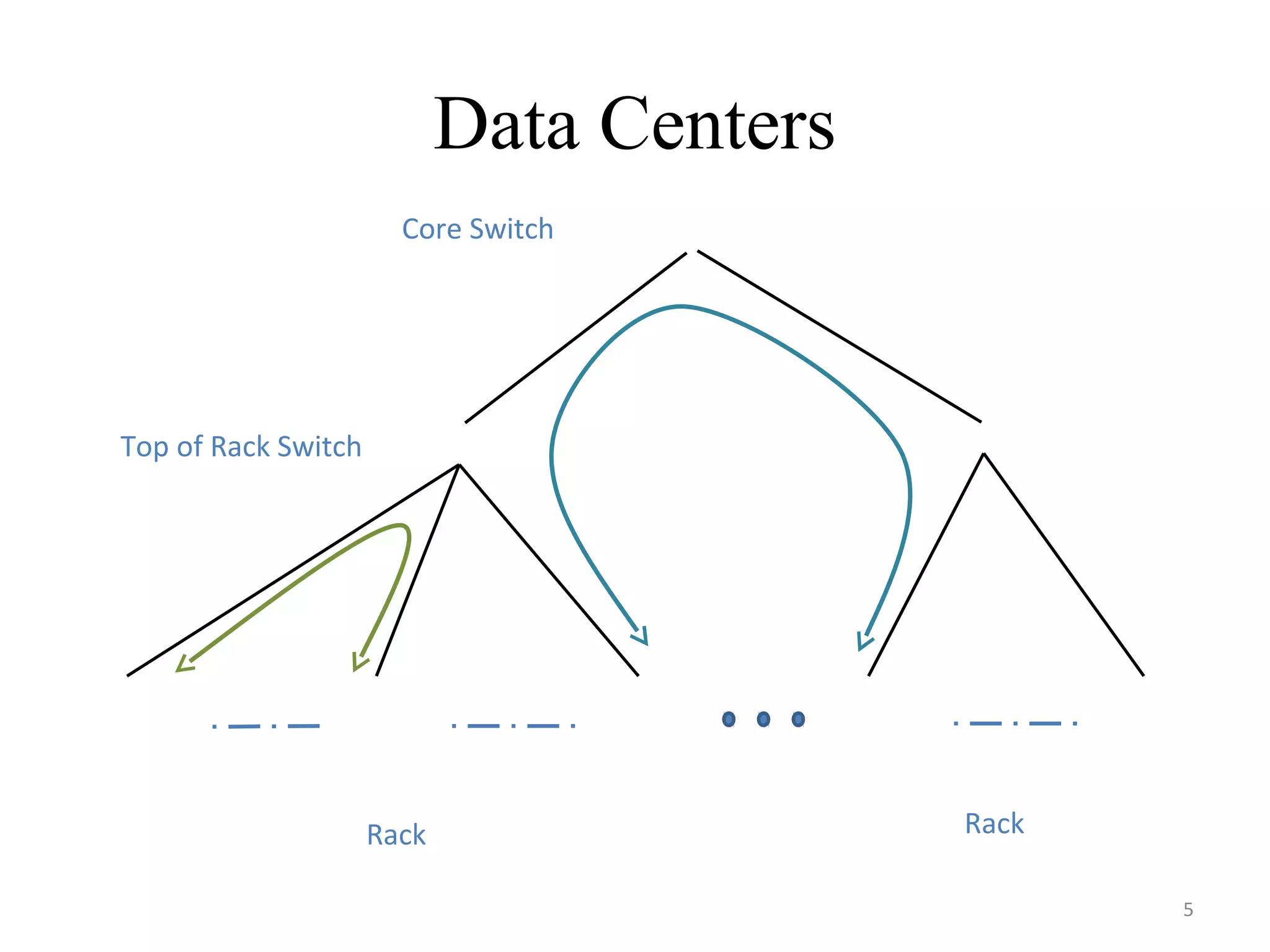
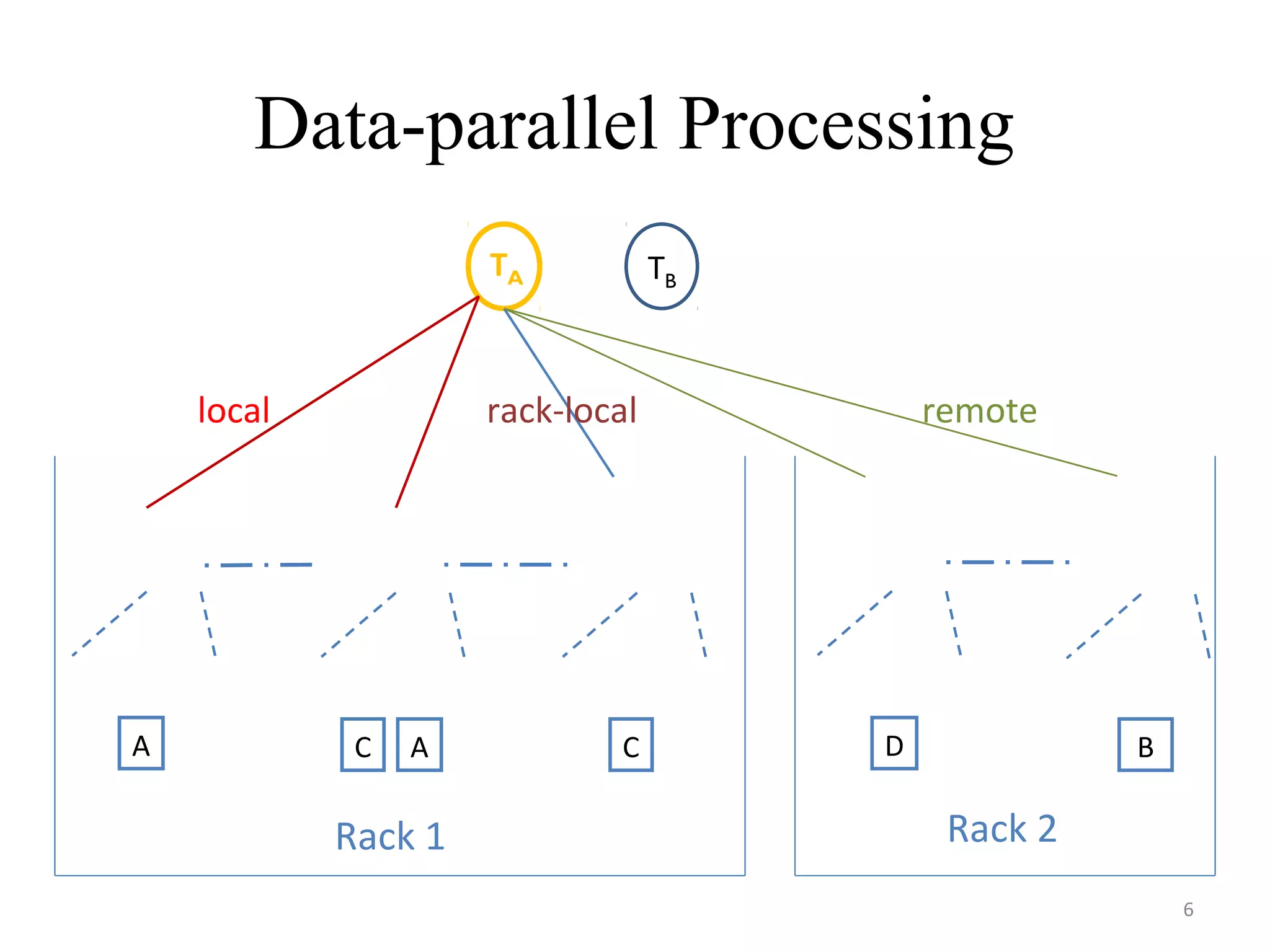
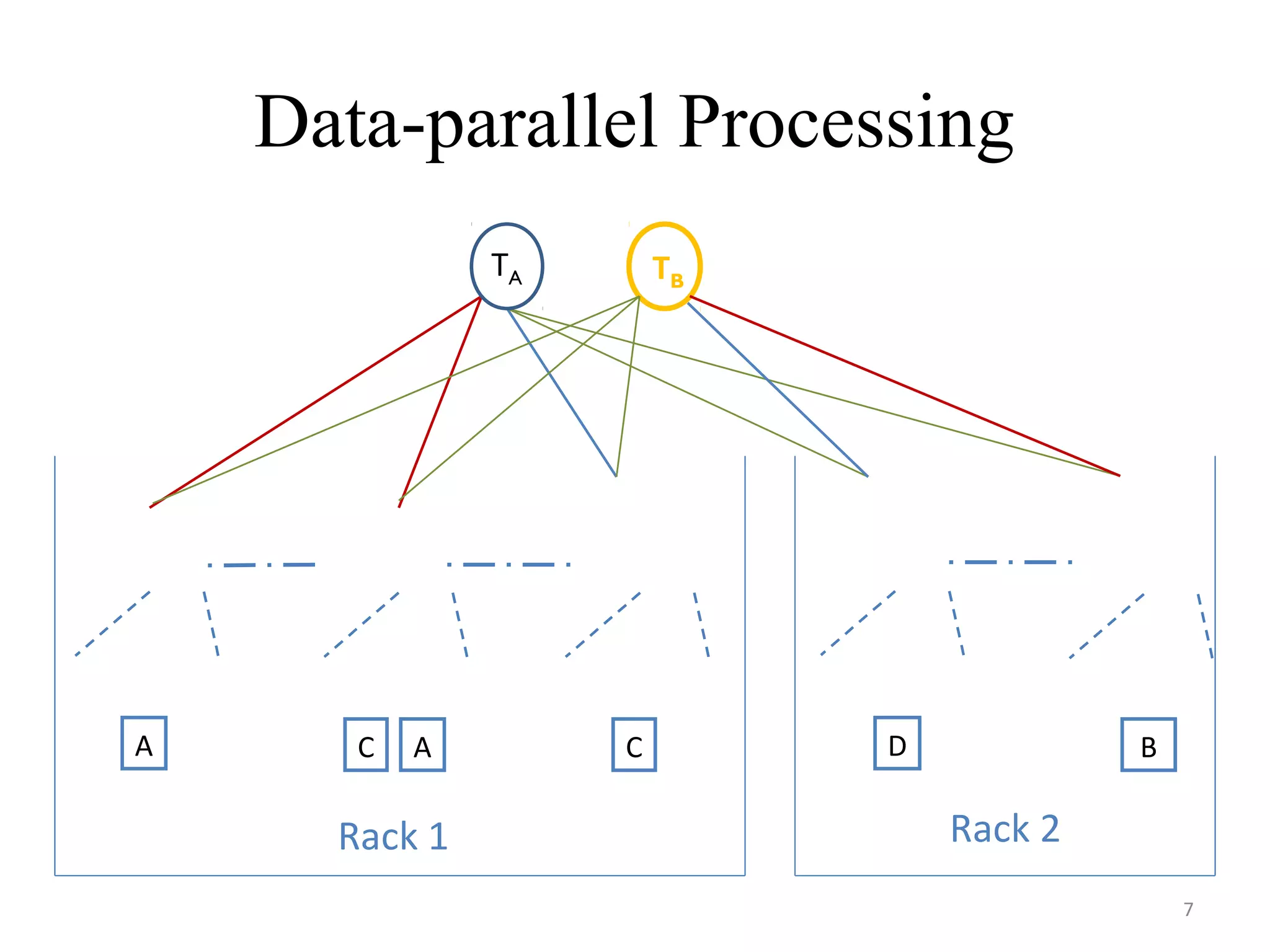
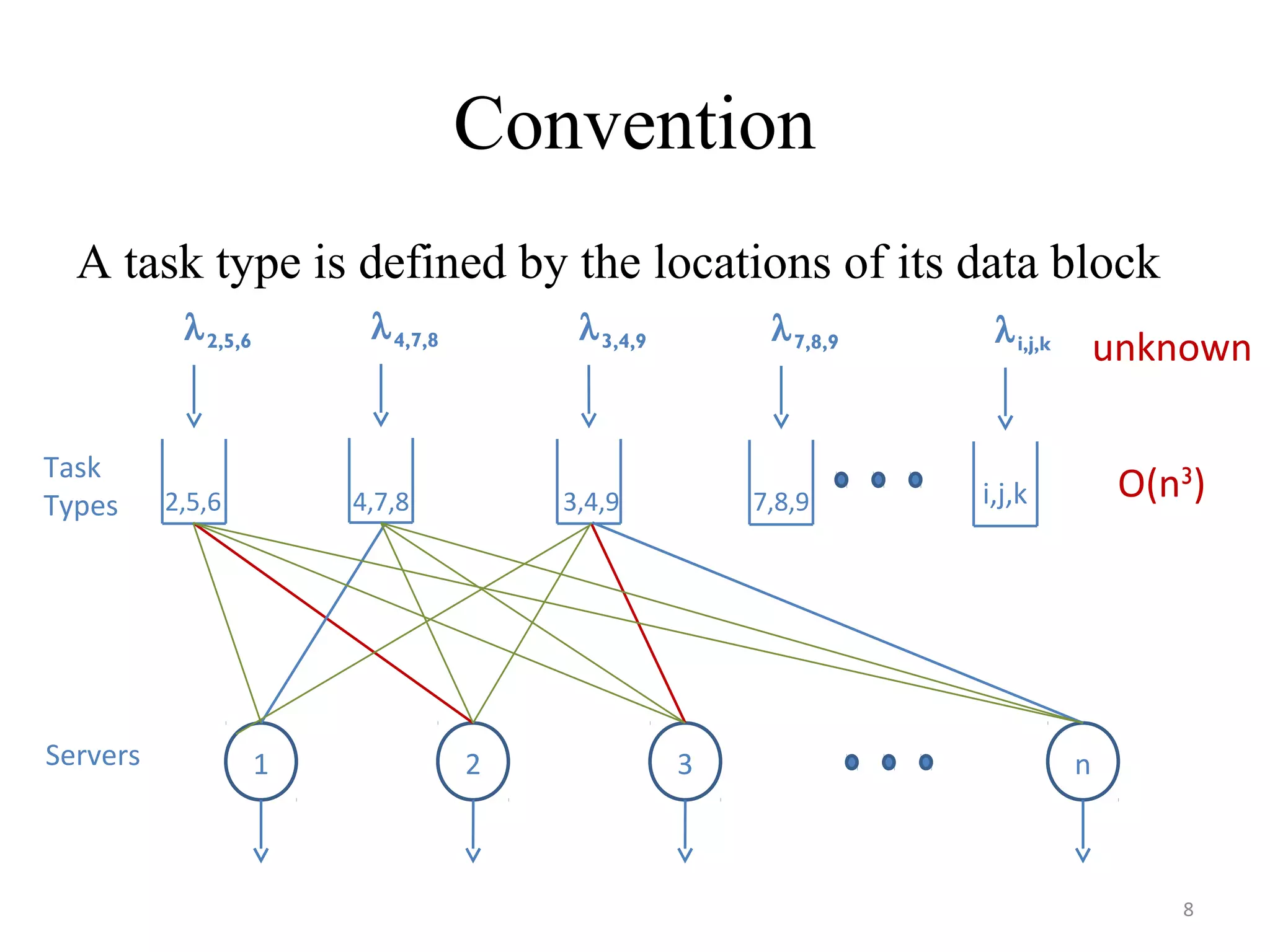
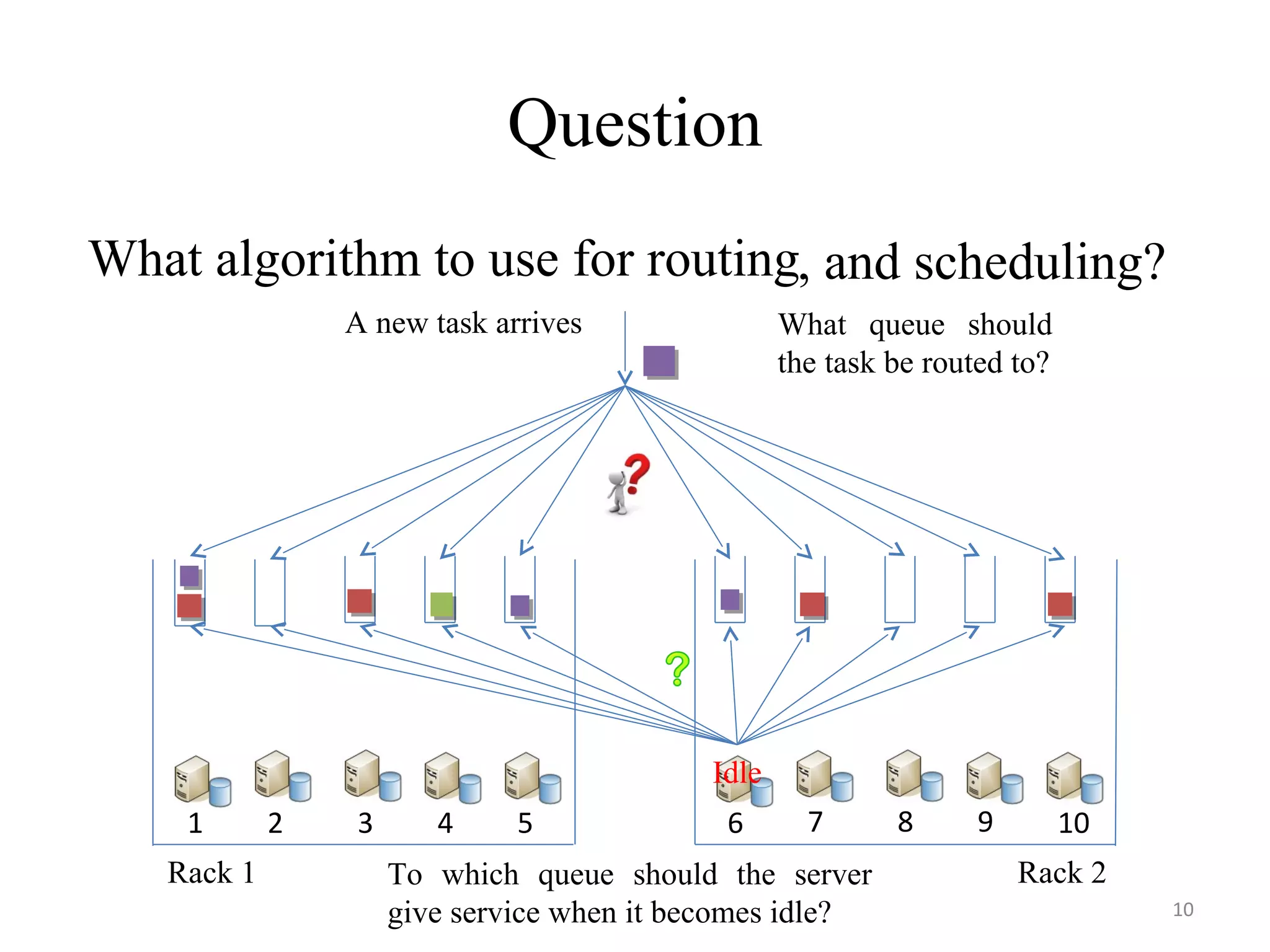
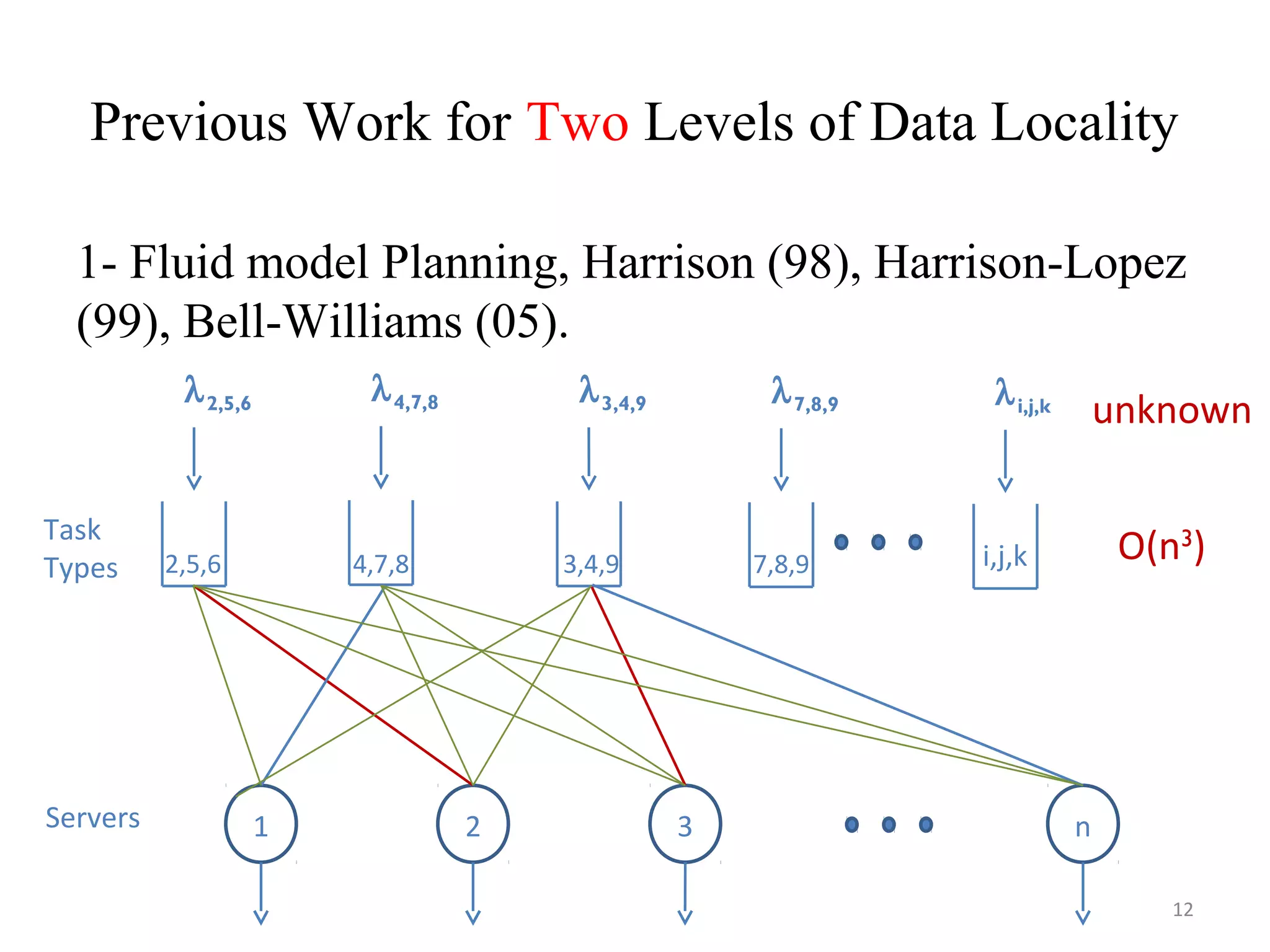
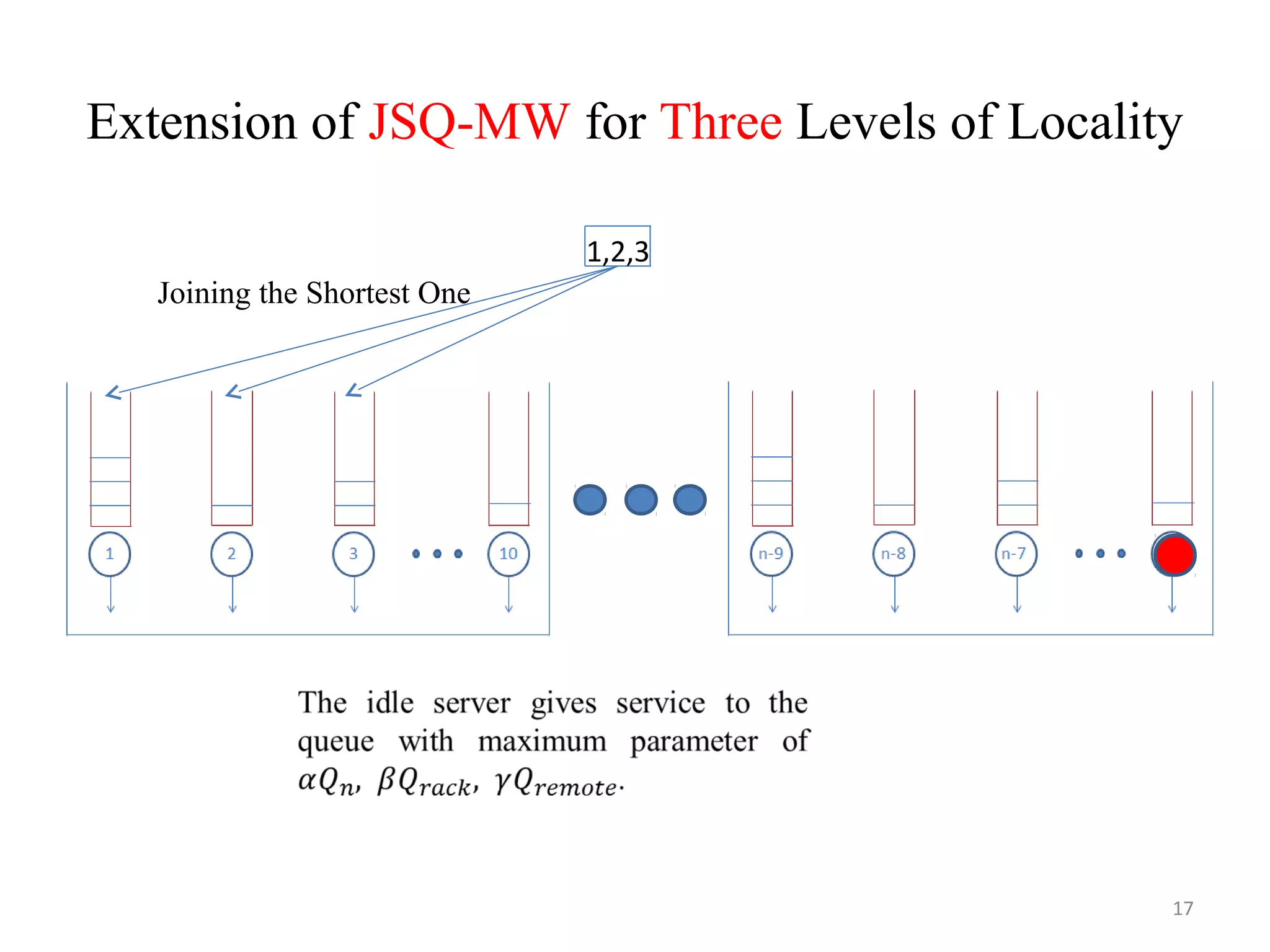
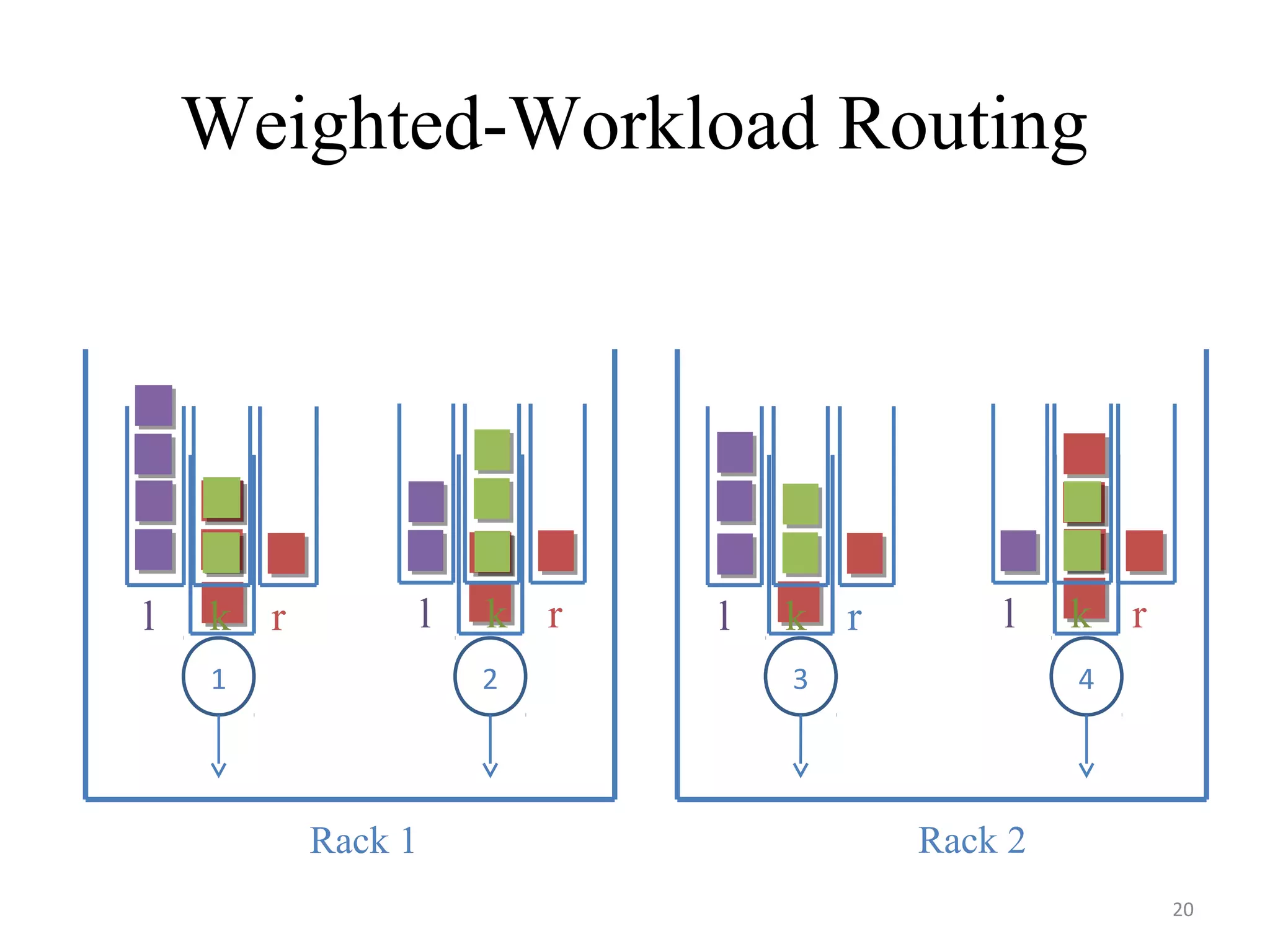
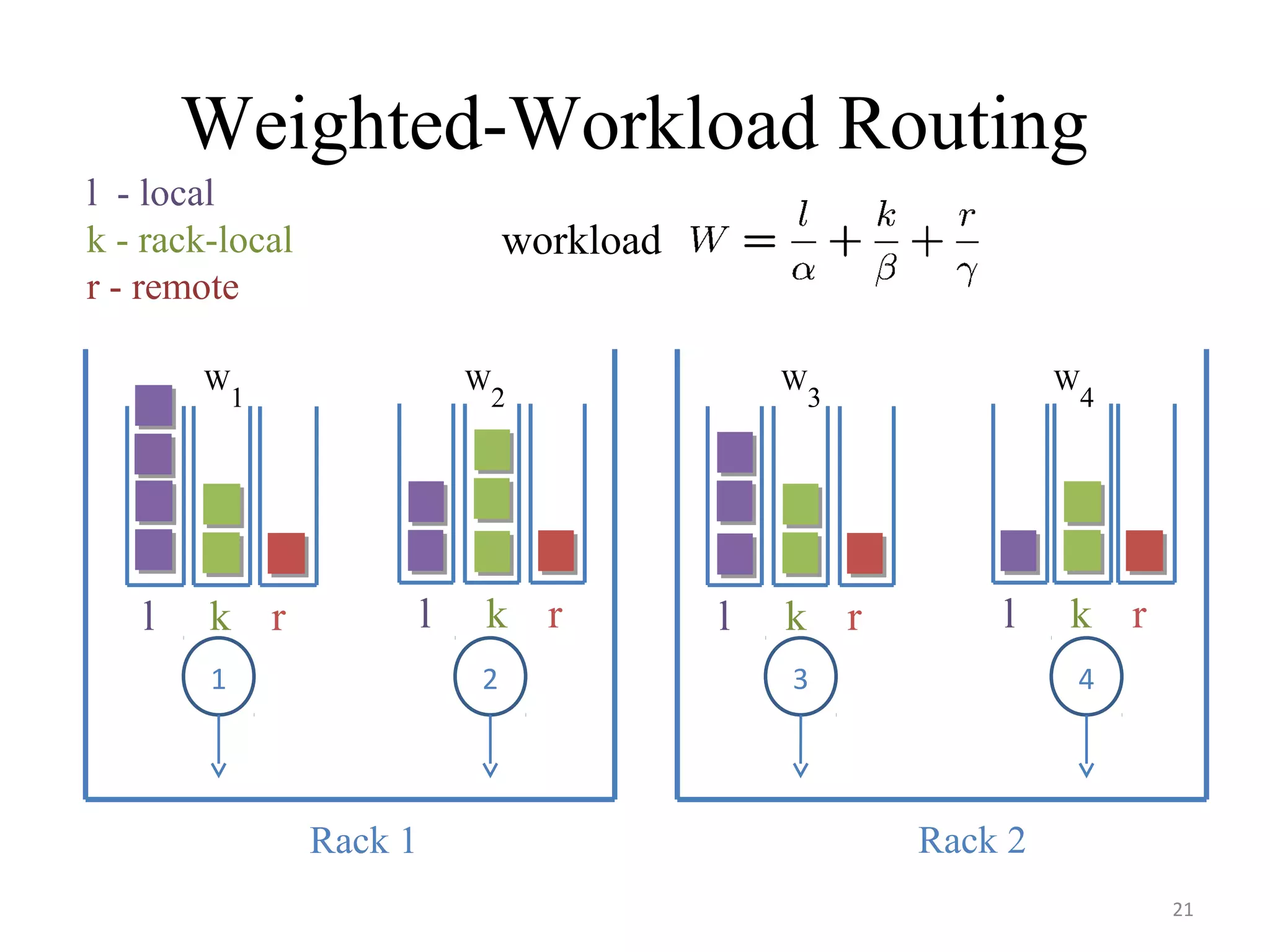
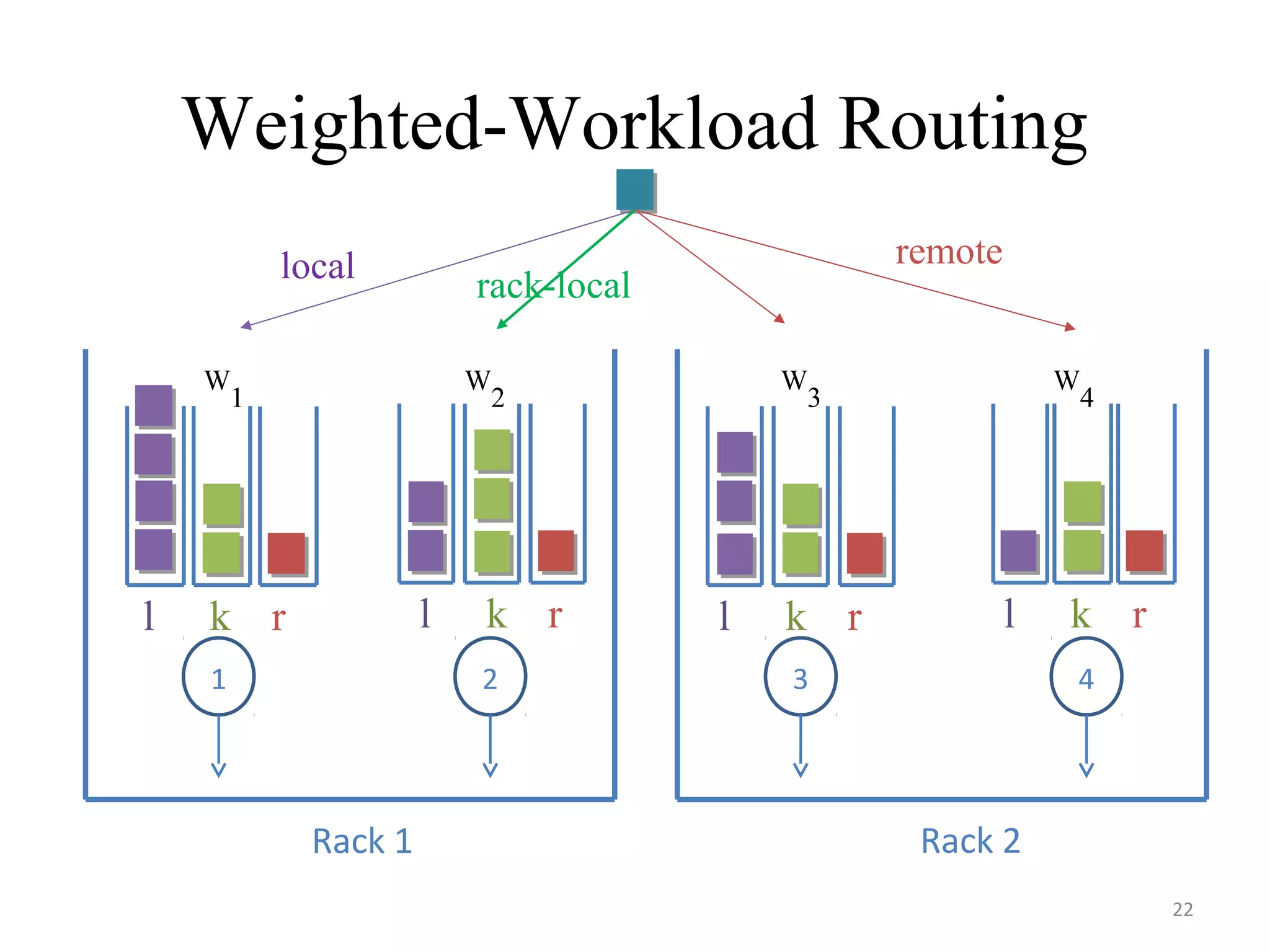
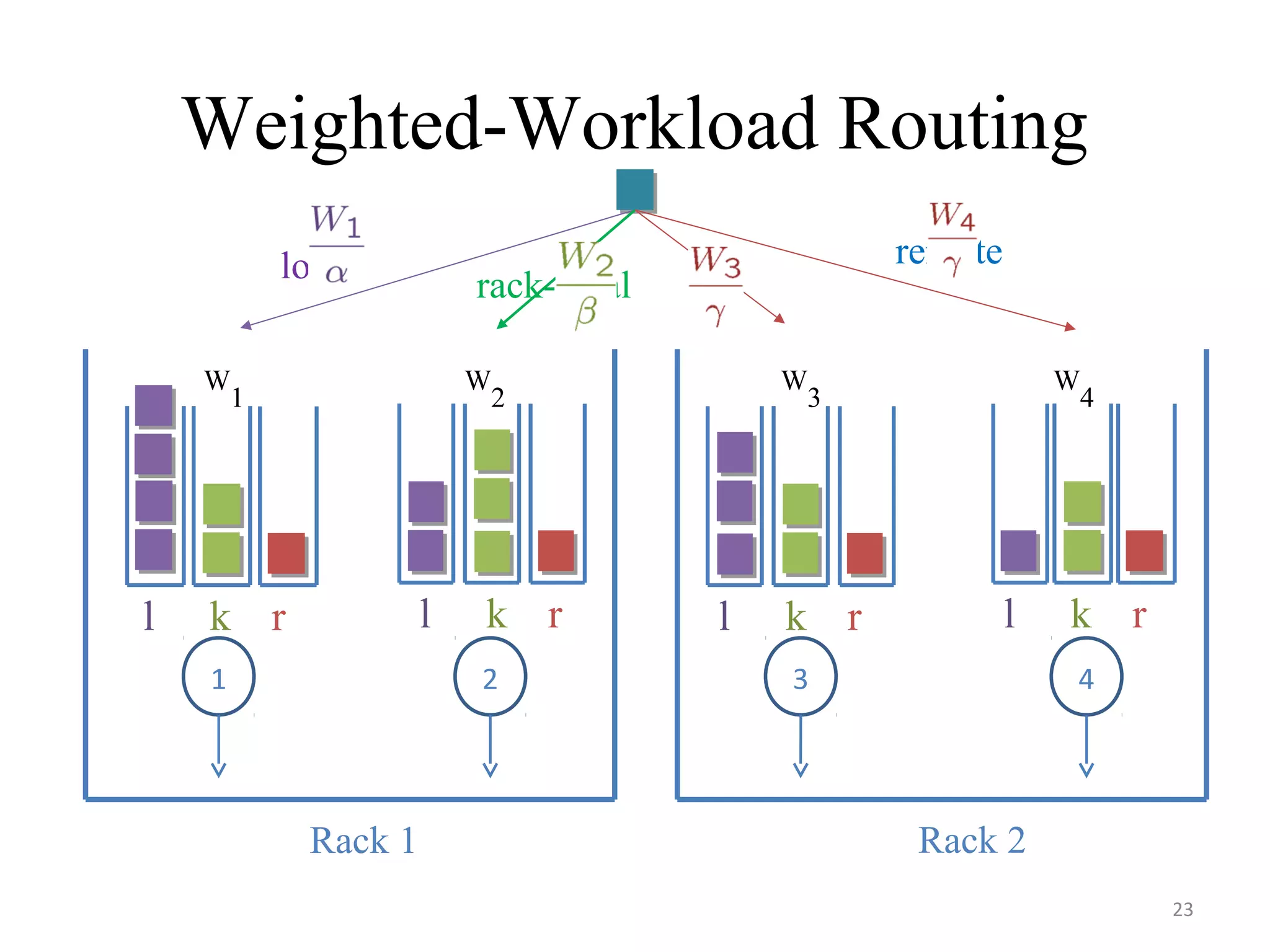
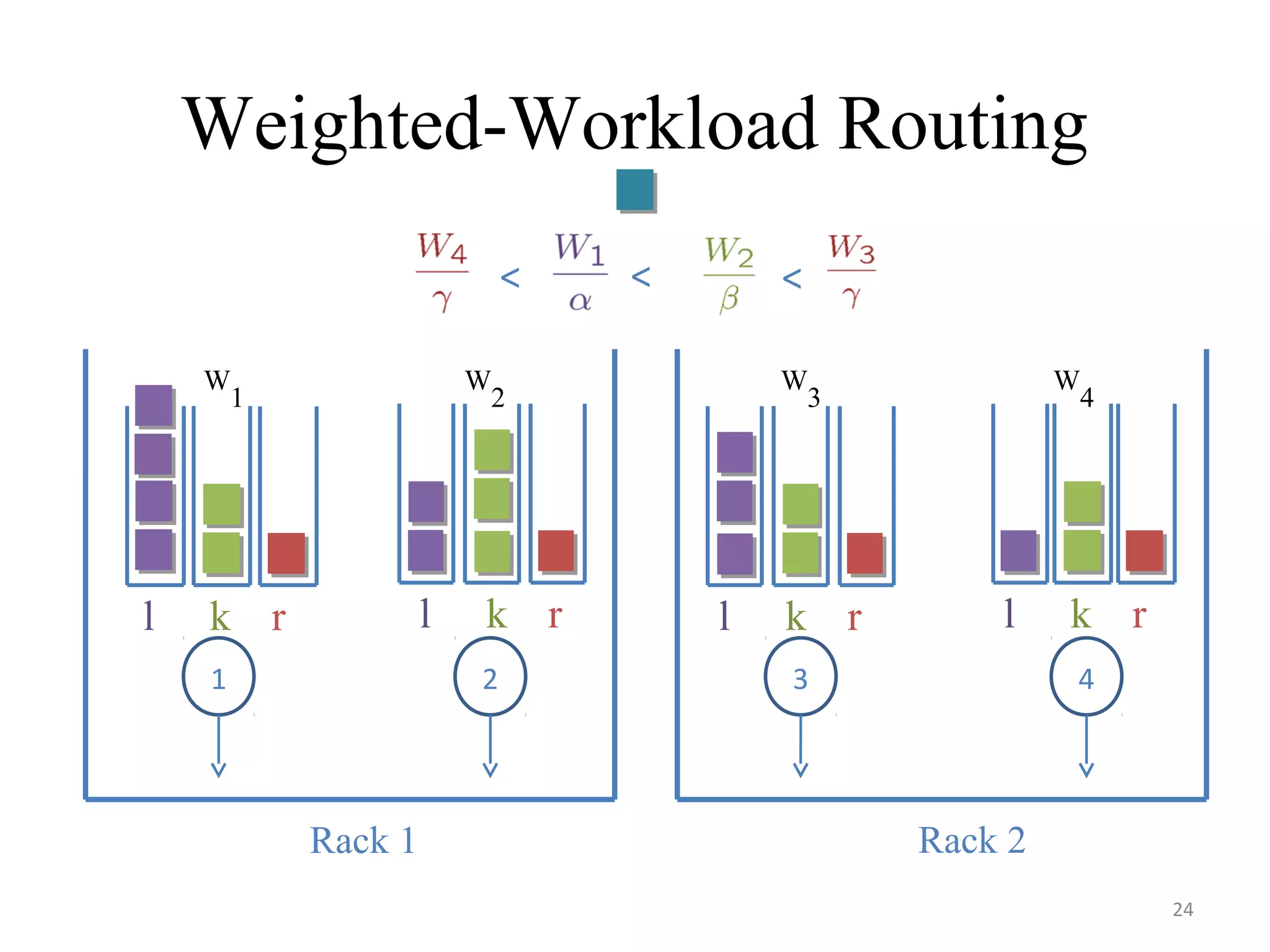
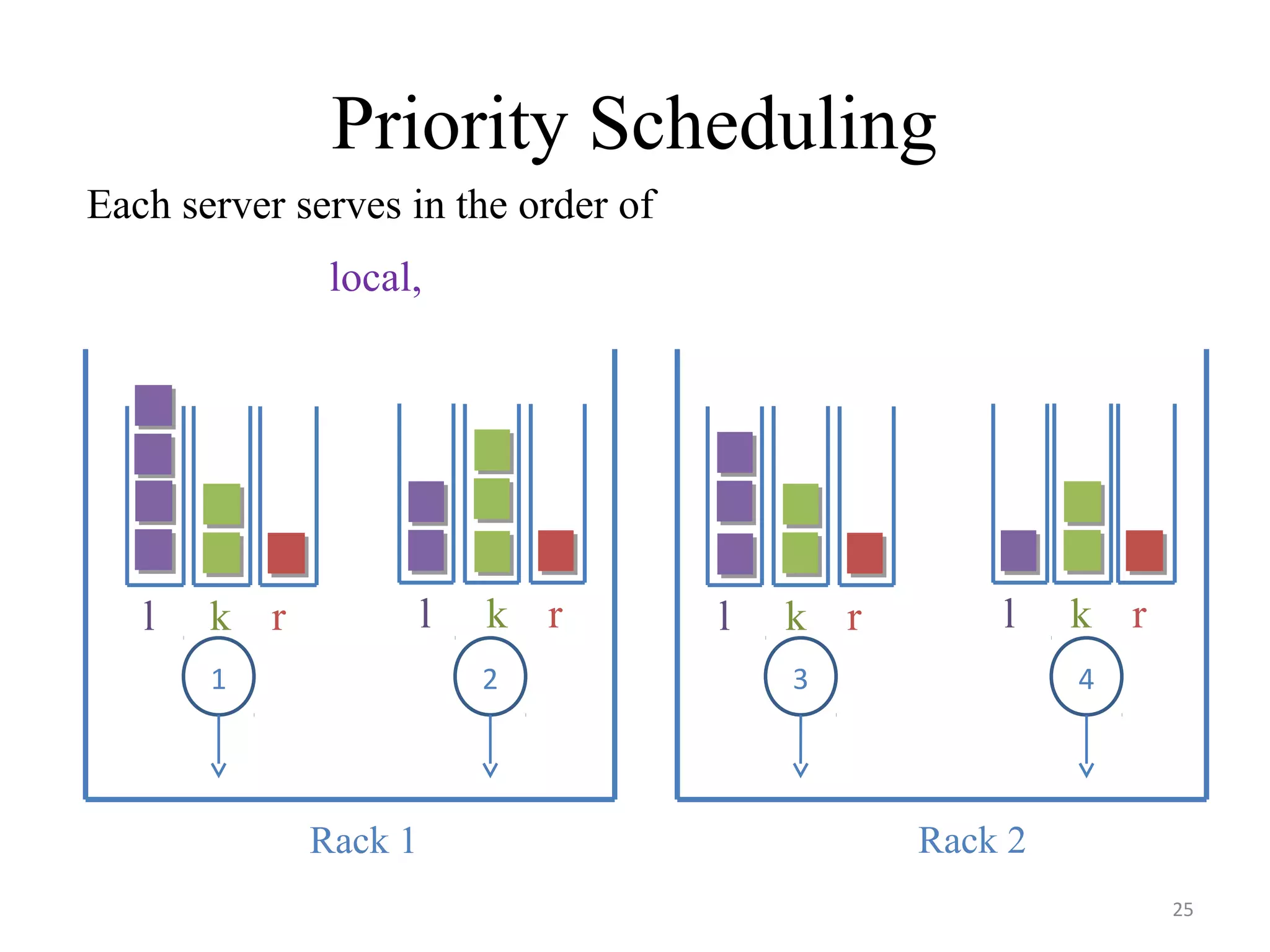
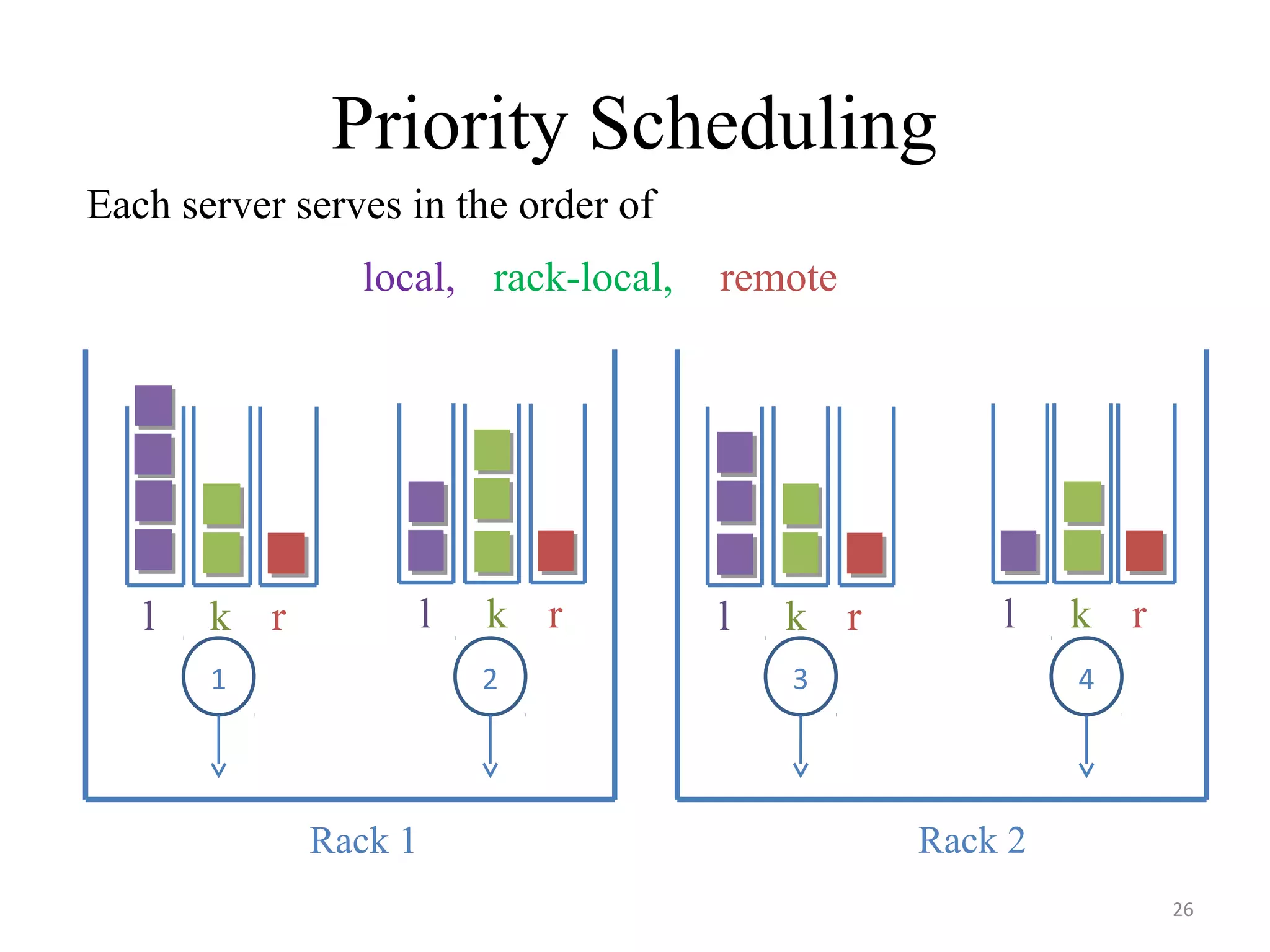
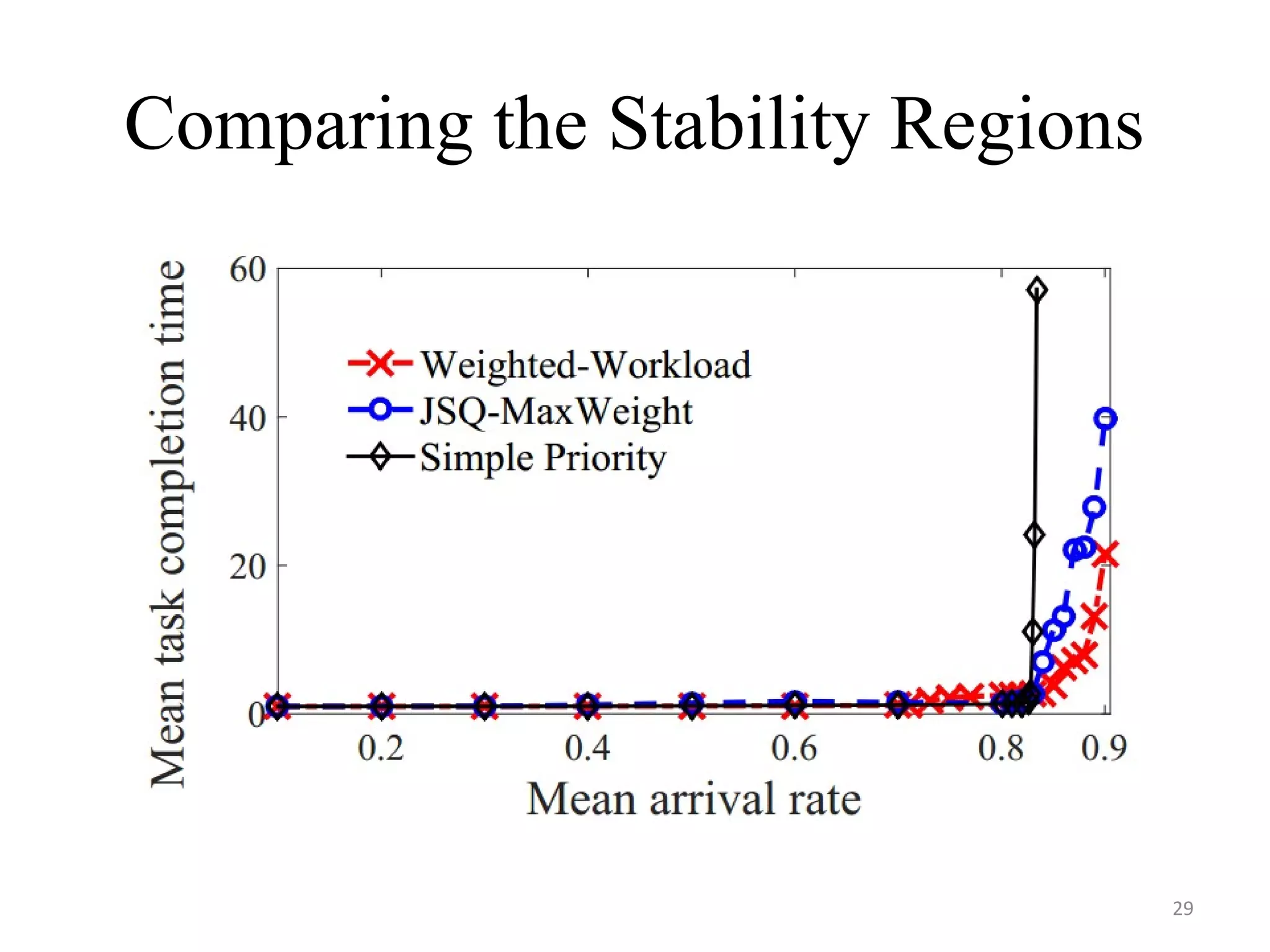
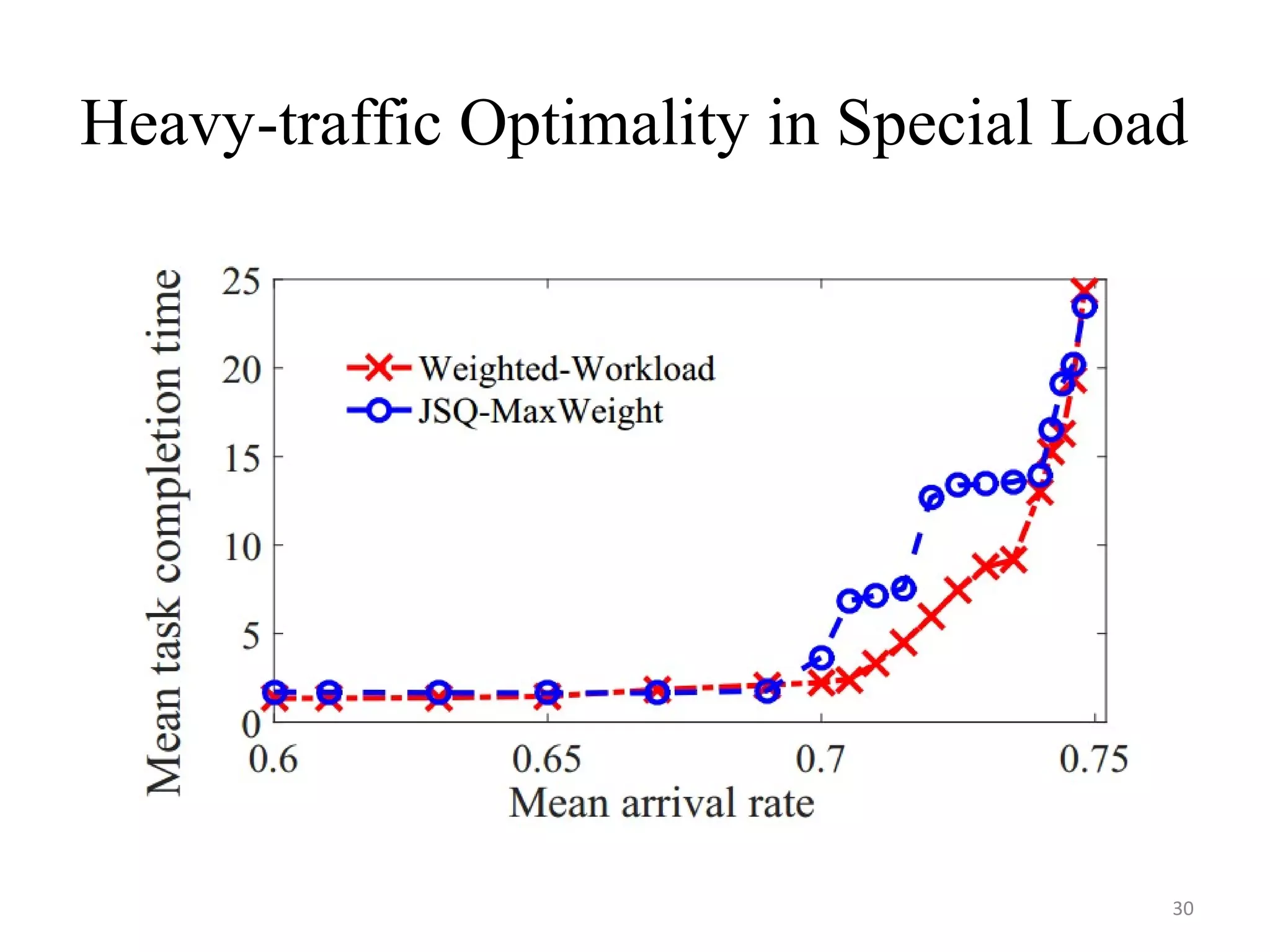
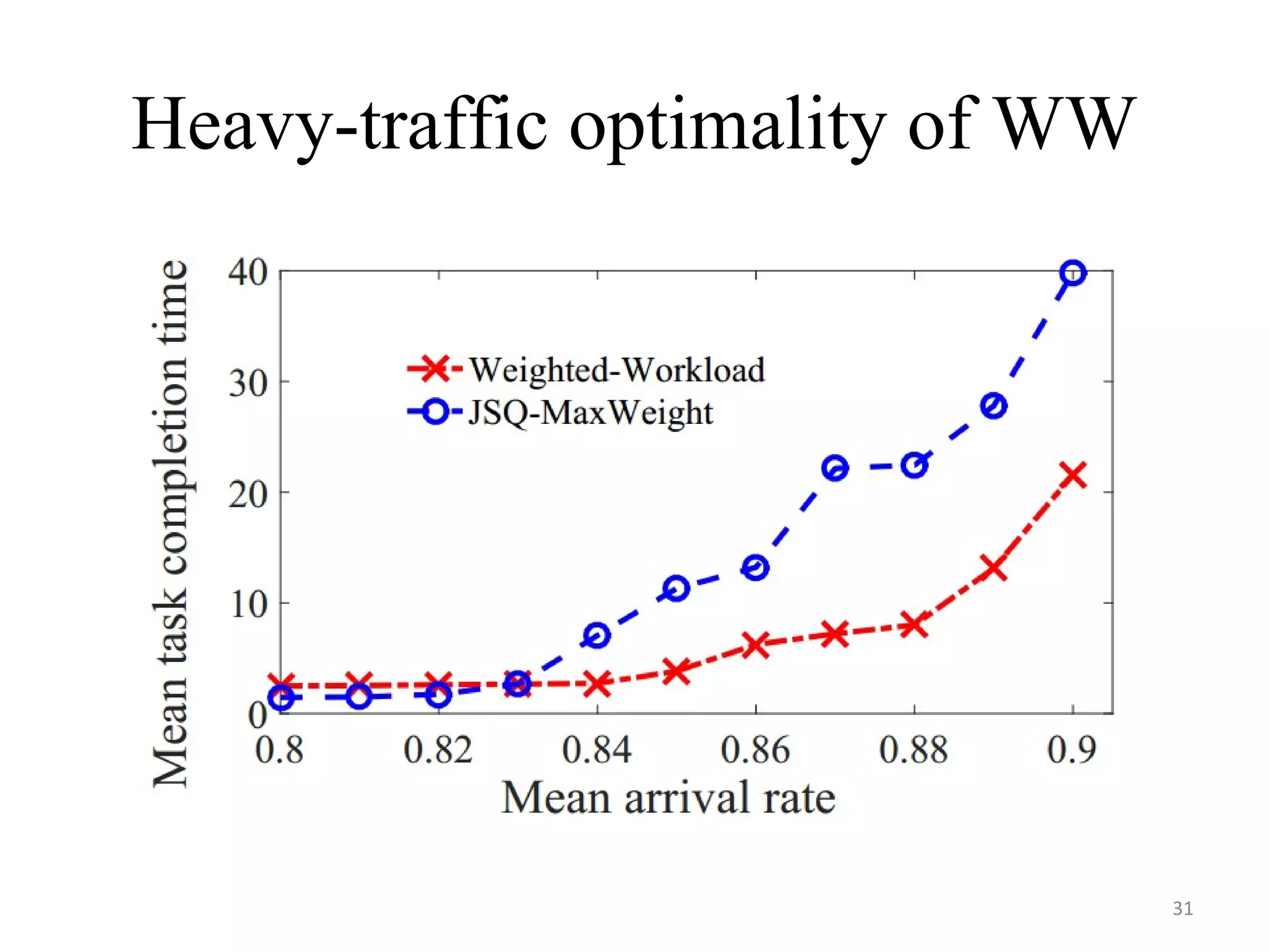
The document discusses scheduling for cloud systems with a focus on multi-level data locality, emphasizing throughput and heavy-traffic optimality. It reviews previous algorithms, such as fluid model planning and join the shortest queue-maxweight, and presents a new algorithm that utilizes weighted workload routing and priority scheduling. The proposed solution aims to optimize data processing efficiency by effectively managing task queues across different levels of data locality.

1. Scheduling for Cloud Systems with Multi-level Data
Locality: Throughput and Heavy-traffic Optimality
Ali Yekkehkhany
In collaboration with Qiaomin Xie, and Professor Yi Lu
University of Illinois at Urbana-Champain (UIUC)
1

2. Data Processing
• Previously, storage and computing were separate
Computing StorageNetwork
2

3. Data-Intensive Processing
Explosion of data sets by industry and research
Computing StorageNetwork
Bottleneck
3

4. Data Centers
• Use separate smaller centers for storage
• Move computing to data
Bottleneck
4

5. Data Centers
Rack Rack
Top of Rack Switch
Core Switch
5

6. Data-parallel Processing
A A BC D
TA TB
C
Rack 1 Rack 2
local rack-local remote
6

7. Data-parallel Processing
A A BC D
TB
C
Rack 1 Rack 2
TA
7

8. Convention
A task type is defined by the locations of its data block
Task
Types
Servers
2,5,6
λ2,5,6
1
4,7,8
λ4,7,8
3,4,9
λ3,4,9
2 3 n
7,8,9
λ7,8,9 λi,j,k
i,j,k O(n3
)
unknown
8

9. Local, Rack-local, and Remote Service
9
1 2 3 4 5 6 7 8 9 10
Rack 1 Rack 2
Task (1, 3, 4)

10. Question
10
1 2 3 4 5 6 7 8 9 10
Rack 1 Rack 2
A new task arrives
, and scheduling?
What queue should
the task be routed to?
What algorithm to use for routing
Idle
To which queue should the server
give service when it becomes idle?

11. Metrics of Optimality for the Algorithm
Throughput Optimality:
Stabilizing any arrival rate vector within capacity
region.
Delay Optimality in Heavy-traffic:
Asymptotically minimizing the average delay as
the arrival rate vector approaches the boundary of
the capacity region.
11

12. Previous Work for Two Levels of Data Locality
1- Fluid model Planning, Harrison (98), Harrison-Lopez
(99), Bell-Williams (05).
12
Task
Types
Servers
2,5,6
λ2,5,6
1
4,7,8
λ4,7,8
3,4,9
λ3,4,9
2 3 n
7,8,9
λ7,8,9 λi,j,k
i,j,k O(n3
)
unknown

13. Previous Work for Two Levels of Data Locality
1- Fluid Model Planning:
1.1 Throughput optimal
1.2 Heavy-traffic optimal
But
NOT practical!
13

14. Previous Work for Two Levels of Data Locality
2- Join the Shortest Queue-Maxweight (JSQ-MW)
Wang et al. (13).
2.1 Throughput optimal
2.2 Not heavy-traffic optimal in all loads
2.3 Heavy-traffic optimal in SPECIFIC loads
14

15. Previous Work for Two Levels of Data Locality
3- Priority Algorithm for Near Data Scheduling
(Pandas), Q. Xie, Y. Lu (15)
3.1 Throughput optimal
3.2 Heavy-traffic optimal for all loads
15

16. Three Levels of Data Locality
1. Fluid Model planning
1. Throughput optimal
2. Heavy-traffic optimal
3. NOT practical!
2. Extension of JSQ-MaxWeight
1. Throughput optimal
2. NOT heavy-traffic optimal for all loads
3. Pandas
1. Not throughput optimal
2. Not heavy-traffic optimal
16

17. Extension of JSQ-MW for Three Levels of Locality
17
1,2,3
Joining the Shortest One

18. Extension of JSQ-MW for Three Levels of Locality
• Extension of JSQ-MaxWeight for systems
with rack structure, Xie et al. (16):
– Throughput optimal.
– Not heavy-traffic optimal in all loads. Just heavy
traffic optimal in specific loads.
18

19. Our Throughput and Heavy-traffic
Optimal Algorithm
• The routing and scheduling for our algorithm
is as follows:
– Routing: Weighted Workload
– Scheduling: Priority Scheduling for Local, Rack-
local, and Remote tasks queued in the 3 queues
associated to each server.
19

20. Weighted-Workload Routing
20
Rack 1 Rack 2
1 2 43
l k r l k rl k r l k r

21. Weighted-Workload Routing
21
1 2
Rack 1 Rack 2
43
l - local
k - rack-local
r - remote
workload
W
1
W
2
W
3
W
4
l k r l k rl k r l k r

22. Weighted-Workload Routing
22
1 2
Rack 1 Rack 2
43
W
1
W
2
W
3
W
4
local
rack-local
remote
l k r l k rl k r l k r

23. Weighted-Workload Routing
23
1 2
Rack 1 Rack 2
43
W
1
W
2
W
3
W
4
local
rack-local
remote
l k r l k rl k r l k r

24. Weighted-Workload Routing
24
1 2 43
W
1
W
2
W
3
W
4
< <<
l k r l k rl k r l k r
Rack 1 Rack 2

25. Priority Scheduling
25
1 2
Rack 1 Rack 2
43
Each server serves in the order of
l k r l k rl k r l k r
local,

26. Priority Scheduling
26
1 2
Rack 1 Rack 2
43
Each server serves in the order of
l k r l k rl k r l k r
local, rack-local, remote

27. Weighted Workload Algorithm
The Weighted Workload (WW) algorithm
proposed by Xie et al. (16) is proved to be both
throughput optimal and heavy traffic optimal in
all loads.
27

28. Evaluation
28

29. Comparing the Stability Regions
29

30. Heavy-traffic Optimality in Special Load
30

31. Heavy-traffic optimality of WW
31

32. References
• [1] Q. Xie, A. Yekkehkhany, Y. Lu. Scheduling with Multi-level Data
Locality: Throughput and Heavy-traffic Optimality. In Proceedings of
INFOCOM. IEEE, 2016.
• [2] Q. Xie, and Y. Lu. Priotrity Algorithm for Near-data Scheduling:
Throughput and Heavy-traffic Optimality. In Proceedings of INFOCOM.
IEEE, 2015.
• [3] W. Wang, K. Zhu, L. Ying, J. Tan, and L. Zhang. Map Task Schedul-
ing in MapReduce with Data Locality: Throughput and Heavy-traffic
Optimality. In Proceedings of INFOCOM. IEEE, 2013.
• [4] J. M. Harrison. Heavy traffic analysis of a system with parallel servers:
Asymptotic optimality of discrete review policies. Annals of Applied
Probability, 1998.
• [5] J. M. Harrison and M. J. L´opez. Heavy traffic resource pooling in
parallel-server systems. Queueing Syst. Theory Appl., 33(4), Apr. 1999.
32

33. Future Work
• Scheduling for multi-level data locality instead
of three levels of data locality.
33

34. Thanks for Your Attention
34

35. Any Questions?!
35
Ali Yekkehkhany
yekkehk2@illinois.edu